Что такое функция в школе

Обновлено: 02.07.2024

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

МЕТОДИКА ПРЕПОДАВАНИЯ ТЕМЫ:

"ФУНКЦИИ В РАМКАХ ШКОЛЬНОГО КУРСА"

Воронеж 2006

Одной из сложнейших тем школьного курса математики являются функции. Появившись в 7-м классе и изучаясь эпизодически, функциональные зависимости в полном объеме предлагаются в 10-11 классах. Предполагается, что старшеклассник, занимаясь функциональным анализом должен совершенно свободно оперировать простейшими функциями. В этот момент возникает большая опасность того, что, работая в данной области математики, ученик займется чисто механической стороной всех исследований, у него сформируется база навыков, совершенно оторванных от реально существующих задач прикладного характера. Если исключить математические классы, то большинство старшеклассников теряется в мире функций, идет отторжение сложного и непонятного материала. В этой ситуации можно попробовать заняться изучением функций прямо с 5-го класса, постепенно приучая к ним ребят и держа постоянную связь с чисто практическими задачами, носящими функциональную окраску.

Подобная практическая окраска функций в рамках школьного курса должна помочь не только формированию прочных знаний в области математики, но и развитию творческого подхода к изучению функционального анализа.

К сожалению, наши выпускники порой не понимают роли математических законов в объяснении фактов, изучаемых на уроках, не обращаются к ним при рассмотрении физических, химических, биологических явлений. Знания о природе у них состоят из множества фактов, явлений, формул, правил не объединенных единой основой.

Надо помочь молодому человеку сформировать у себя основополагающие понятия всех изучаемых наук, понятия, которые входят в состав ядра естественных наук, в "золотой фонд" естественно-научного образования и которые будут способствовать созданию единого взгляда на мир.

В сознании человека знания об окружающем мире не просто преломляются как "солнце в малой капле вод", они во многом формируют отношение человека к миру, влияют на его нравственные качества, особенно в детском возрасте. Не просто знания о природе, а глубокое проникновение в тайны природы, через которые раскрывается обаяние науки, возникает благоговение перед нею - вот что имеет воспитательную силу, может помочь ученику полюбить идею и истину, помогает ставить духовные наслаждения выше телесных, духовные достоинства - выше наружного блеска внешней оболочки.

Научное обоснование проблемы на базе исследования

психологических аспектов развития учащихся

Предлагаемая мною методика ведения "Функций" применима при работе с любым учебником математики 5-го класса, включая учебник Л. Г. Петерсон. Автор там пытается проводить функциональную линию уже с первого класса, но она ограничивается лишь введением таблиц и обучением чтению графика функции (это отрабатывается в течение 4 лет). Подобная практическая подготовка облегчит введение самого понятия функции в 5 классе и позволит расширить чтение предложенных графиков функций до начальных этапов исследования функциональных зависимостей по графикам.

Прежде чем будет изложена сама идея рассмотрения функции с 5-го класса, хотелось бы поговорить о психологических особенностях учеников, вызвавших мысль о подобной работе в рамках теории функции.

Попытка ввести функции раньше 5-го класса просто неосуществима в силу наличия у детей до 9-10 лет лишь репродуктивных образов-представлений об известных объектах или событиях не воспринимаемых в данный момент времени. Причем эти образы в основном статичны, и заставить ребенка представить динамику изменений двух взаимосвязанных величин, да еще обобщить ее до функциональной зависимости невозможно.

Исследовательский характер введения понятия функции естественно будет раскрываться учителем с помощью диалога, а это как нельзя лучше поможет разрешить проблему перехода ученика к новой ступени самостоятельности от начальных классов к среднему звену, будет способствовать психологическому выравниванию ребят в связи с их переходом к новому учителю.

К 13-14 годам у учеников появляется возможность заниматься теоретическими рассуждениями и самоанализом. Отмечается способность к дедукции и индукции, формируются важнейшие интеллектуальные приобретения - это умение оперировать гипотезами, появляется теоретическое мышление. Вот именно тогда и стоит переходить от практических функциональных задач к абстракциям мира зависимостей. Здесь можно вводить строгое определение функции.

С переходом в среднее звено школы изменяется положение детей в системе деловых и личных взаимоотношений с окружающими людьми. Все больше времени в их жизни начинают занимать серьезные дела. Возрастают требования к интеллекту ребенка, которые одновременно предъявляют и его сверстники, и взрослые люди. Учителя и родители начинают переходить на новый стиль общения с подростками, больше апеллируя к их разуму и логике. Почувствовать себя увереннее, самостоятельнее и значимее для себя и для других поможет работа с функциями, где ученик исследует, анализирует и делает выводы в соавторстве с учителем, а в последствии и самостоятельно. Именно работа с функциями и математическим моделированием является интересной и интеллектуально захватывающей деятельностью.

На интересной, интеллектуально захватывающей деятельности или на такой работе, которая мотивирована соображениями престижности, подростки могут длительное время удерживать внимание, быть в состоянии переключать или распределять его между несколькими действиями и поддерживать довольно высокий темп работы. Поэтому уже с 6-7 классов не стоит бояться достаточно серьезно разговаривать с учениками на темы, связанные с функциональным анализом. Это наоборот будет стимулировать ожидание взросления, поможет формированию уважения к самому процессу исследования.

В подростковом возрасте происходят важные процессы, связанные с перестройкой памяти. Вследствие появления в школе многих новых учебных предметов значительно увеличивается количество информации, которую должен запоминать подросток, в том числе механически. У него возникают проблемы с памятью, и жалобы на плохую память в этом возрасте встречаются намного чаще, чем у младших школьников.

К сожалению, по существующей программе именно этот период приходится на начало введения понятия функций и сопровождающие дополнительные определения. Здесь впервые и возникает серьезное отторжение нового материала и, как следствие, блокировка его изучения в будущем. Давняя же дружба с функциями (начиная с 5-го класса) позволит пережить эти неприятные моменты менее болезненно.

Исследования памяти детей данного возраста (13-15 лет) показали, что для подростка вспоминать – значит мыслить. Его процесс запоминания сводится к мышлению, к установлению логических отношений внутри запоминаемого материала, а припоминание заключается в восстановлении материала по этим отношениям, поэтому, воспоминания о функциях 5-6 классов в 7-8 классе должны дать хорошие плоды (теоретический материал будет основываться на базе двухлетней практической работы).

Именно в подростковом возрасте появляется склонность к экспериментированию, проявляющаяся, в частности, в нежелании все принимать на веру. Подростки обнаруживают широкие познавательные интересы, связанные со стремлением все самостоятельно перепроверить, лично удостовериться в истинности. Прекрасно! Предлагайте им серию практических работ с последующим выходом на математические конференции. Ведь именно подростковый возраст отличается повышенной интеллектуальной активностью, которая стимулируется не только естественной возрастной любознательностью подростков, но и желанием развить, продемонстрировать окружающим свои способности, получить высокую оценку с их стороны. В этой связи, подростки на людях стремятся брать на себя наиболее сложные и престижные задачи, нередко проявляют не только высоко развитый интеллект, но и незаурядные способности.

Для них характерна эмоционально-отрицательная аффективная реакция на слишком простые задачи. Такие задачи их не привлекают, и они отказываются их выполнять из-за соображений престижности. А этого делать не придется. Хорошая практическая база 5-7 класса позволит уже с 8 класса погрузиться в мир абстракций функциональных зависимостей и общаться с учащимися, используя серьезные теоретические выводы, основанные на трехлетней исследовательской работе. Естественный интерес, повышенную любознательность детей данного возраста следует использовать в активном привлечении учащихся к поиску функций за рамками школьного учебника (в химии, физике, биологии, и т.д.). Если удастся в этом возрасте (14-15 лет) приступить к формированию единого восприятия мира, поиску межпредметных связей, то это поможет в последствии в становлении высоко развитых интеллектуальных личностей, видящих целостную картину процесса познания.

Вопросы, которые задает подросток взрослым детям, учителям и родителям, нередко достаточно глубоки и касаются самой сути вещей.

Подростки могут формулировать гипотезы, рассуждать предположительно, исследовать и сравнивать между собой различные альтернативы при решении одних и тех же задач. Сфера познавательных, в том числе учебных, интересов подростков выходит за пределы школы и приобретает форму познавательной самодеятельности - стремления к поиску и приобретению знаний, к формированию полезных умений и навыков. Подростки находят занятия и книги, соответствующие их интересам, способные дать интеллектуальное удовлетворение. Стремление к самообразованию — характерная особенность: и подросткового, и раннего юношеского возраста. Задача учителя, лишь поддержать воспитанника в этот период как можно большей похвалой и возвеличиванием его поисков новых решений и новых тем в области математики.

Самостоятельность мышления проявляется в независимости выбора способа поведения учителя. Подростки и особенно юноши принимают лишь то, что лично им кажется разумным, целесообразным и полезным, поэтому надо успеть за 5-7 класс (пока все принимается на веру) убедить ребенка в том, что функции действительно нужны, что мир, окружающий нас состоит из зависимостей и познать их - наша задача. Лишь тогда в старших классах появится возможность серьезно заниматься функциональным анализом, не боясь, что этот материал будет всего лишь навязан учителем.

Мы знаем, как соответствовать определенным чертам: быть вежливым, опрятным, инициативным. А как быть соответствиям между числовыми множествами — узнаем в этой статье про математические функции.

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, функция у = 2х каждому действительному числу x ставит в соответствие число y, которое в два раза больше, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Титарева Галина Александровна
Брянский государственный университет имени академика И.Г. Петровского
магистрант

Понятие функции является одним из основных в науке и имеет мировоззренческое и общекультурное значение. Благодаря ему можно изучать физические величины в их взаимосвязи, а с помощью свойств функций решать математические задачи. Кроме того, изучение естествознания и техники также немыслимо без функций. Их широкая применимость обусловила введение учения о функциях в школьный курс математики.

Еще в XVII веке идея функции встречается у Рене Декарта. Он ввел данный термин в 1673г., и понятие функции первоначально носило геометрический характер. С появлением таких ученых, как Бернулли и Эйлер, понятие функции приобретает аналитический характер. Современное определение функции трактуется как соответствие между множествами любой природы, в курсе алгебры оно имеет название – определение Дирихле-Лобачевского.

С течением времени были хорошо изучены элементарные функции, которые теперь изучаются в школе.

Функция называется элементарной, если ее значения могут быть получены из постоянных чисел и значений независимых переменных посредством конечного числа элементарных операций [1, с.13]. В их число входят следующие функции (Рисунок 1):

1) алгебраические функции (степенные с любым действительным показателем);

2) трансцендентные функции (показательная и логарифмическая функции, тригонометрические и обратные тригонометрические функции).

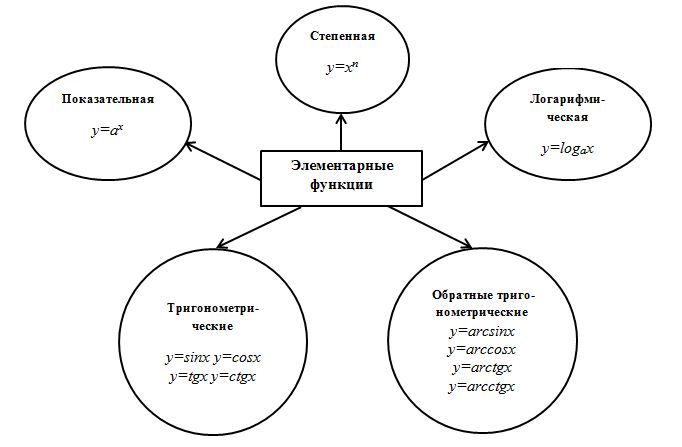
Рисунок 1. Элементарные функции

Трактовки понятия функция делятся на 2 вида:

1) классические – опираются на понятие переменной величины (функция – переменная величина, числовое значение которой изменяется в зависимости от числового значения другой [2, с. 258]);

2) современные (если каждому элементу х множества М поставлен в соответствие некоторый элемент y множества N, то говорят, что на множестве М задана функция, и пишут: у=f(x) [3, с.2]).

Классическое определение, называющее функцией переменную величину, зависящую от другой переменной величины (аргумента), подходит к обычным аналитическим числовым функциям, изучаемым в школьном курсе математики, является традиционным и часто применяется в преподавании.

Стоит обратить внимание и на базовые модели теории функций. В их число входят функции, определенные на данных множествах:

1) на числовом множестве;

2) на множестве точек геометрического пространства;

3) на множестве двоичных последовательностей;

4) на множестве векторов;

5) на множестве геометрических фигур;

6) на множестве событий.

Проблема изучения понятия функции в школе является очень актуальной. Многие педагоги и методисты выделяют его как фундаментальное математическое понятие. Стоит отметить выступление педагога высшей немецкой школы Феликса Клейна, который главной целью обучения ставил необходимость обеспечить усвоение понятия функции еще на ранних этапах. По его мнению, оно должно пронизывать все преподавание алгебры и геометрии, то есть играть руководящую роль в школьном курсе математики.

И все же несомненную ценность представляет и ряд других понятий, которые должны получить самостоятельное развитие в ходе обучения. В их числе находятся понятия следующих содержательно-методических линий: линии числа, преобразований курса алгебры и начал анализа, линии уравнений, неравенств и их систем. Немаловажно также развитие логического мышления учащихся. Нет необходимости выделять какую-либо одну из представленных идей школьного курса математики и давать ей развитие за счет других, ведь все эти теории изучаются во взаимосвязи.

Безусловно, изучение функций развивает функциональное мышление учащихся, дети знакомятся с идеей всеобщей непрерывности, бесконечности, формируют у себя умения анализировать, находить зависимости между изменениями различных объектов, работать с абстрактным материалом. Изучение свойств функций позволяет познавать явления окружающего мира. Но в младших классах ученики могут оказаться неподготовленными к восприятию понятия функции в силу своего недостаточного математического развития. Это только повлечет за собой затраты времени на дополнительное объяснение, что ставит под сомнение идею Ф. Клейна.

В школе основное внимание уделяется числовым функциям. Понятие соответствия, лежащее в основе определения понятия функции, доступно учащимся 5 класса. При решении текстовых задач ученики используют различные функциональные зависимости.

Среди зависимостей наиболее часто встречаются следующие:

1) цена, вес и стоимость;

2) скорость, время и расстояние;

3) стороны прямоугольника и его площадь;

4) стороны прямоугольника и его периметр;

5) работа, время работы и оплата и т. д.

В школе чаще всего используются аналитический и формальный походы к изучению функций, поэтому учащиеся запоминают определения и формулировки свойств, не подкрепляя их образами. Нужно больше внимания уделять графикам функций, с их помощью легче будет понять многие свойства функций, такие, как нули функции, монотонность, область значений функции.

Понимание функции как математической модели реальных процессов определяет общекультурный аспект изучения математики. В связи с этим учащиеся должны уметь видеть функциональную зависимость не только в алгебраических формулах, но и в других школьных предметах и в жизни. Такое построение учебного материала отвечает принципу целостности образования[2, с.264].

Сформированность понятия функциональной зависимости у учащихся – это важная задача целевой деятельности педагога. Она направлена на становление математического мышления и развитие творческой деятельности учеников. Развитие функционального мышления главным образом предполагает формирование способностей к овладению общими учебными приемами и умениями, обнаружению новых связей.

МЕТОДИКА ИЗУЧЕНИЯ ПОНЯТИЙ Введение понятия функции в средней школе Понятие функции является одним из важнейших понятий в средней школе. Как правило, определение функции дается в седьмом классе, а затем это понятие уточняется на протяжении всего курса школьной математики до одиннадцатого класса.

Введение понятия функции в средней школе

Понятие функции является одним из важнейших понятий в средней школе. Как правило, определение функции дается в седьмом классе, а затем это понятие уточняется на протяжении всего курса школьной математики до одиннадцатого класса.

В 10 классе подводится итог знаний о функции, которые были даны прежде. Рассматриваются основные свойства функции, общая схема исследования функции. Вводятся понятия: целая рациональная и дробно-рациональная функции. Вводятся тригонометрические функции, и, наконец, показательные и логарифмические функции. Все эти функции рассматриваются только как функции одной переменной, причем сами переменные не выходят за рамки множества вещественных чисел.

Введение понятия функции - длительный процесс, завершающийся формированием представлений о всех компонентах этого понятия в их взаимной связи и о роли, играемой им в математике и в ее приложениях. Этот процесс ведется по трем основным направлениям:

- упорядочение имеющихся представлений о функции, развертывание системы понятий, характерных для функциональной линии (способы задания и общие свойства функций, графическое истолкование области определения, области значений, возрастания и т. д. на основе метода координат);

- глубокое изучение отдельных функций и их классов;

- расширение области приложений алгебры за счет включения в нее идеи функции и разветвленной системы действий с функцией.

Первое из этих направлений проявляется в курсе школьной алгебры ранее остальных.

В реализации этого направления значительное место отводится усвоению важного представления, входящего в понятие функции, -- однозначности соответствия аргумента и определенного по нему значения функции. Для рассмотрения этого вопроса привлекаются различные способы задания функции.

Чаще других в математике и ее приложениях применяется задание функции формулой. Все другие способы играют подчиненную роль. Именно поэтому после первого знакомства с несколькими такими способами основное внимание в обучении уделяется тем функциям и классам, которые имеют стандартную алгебраическую форму их выражения.

Однако при введении понятия, сопоставление разных способов задания функции выполняет важную роль. Во-первых, оно связано с практической потребностью: и таблицы, и графики, как правило, служат для удобного в определенных обстоятельствах представления функции, имеющей аналитическую форму записи. Во-вторых, оно важно для усвоения всего многообразия аспектов понятия функции. Формула выражает функцию лишь будучи включенной в соответствующую систему представлений и операций, а эта система такова, что различные компоненты понятия функции могут быть отображены наиболее естественно различными средствами.

Использование перевода задания функции из одной формы представления в другую - необходимый методический прием при введении понятия функции.

Реализация этого приема состоит в использовании системы заданий, в которых представлены все случаи такого перевода. Если ограничиться основными способами представления функции - формулой, графиком, таблицей, то получится 6 типов упражнений, при которых форма представления меняется, и 3 - при которых она остается такой же.

Одна из распространенных трудностей, которую приходится преодолевать начинающему знакомиться с понятием функции, связана с заданием функций графиками и формулами. Эта трудность заключается в следующем: как можно говорить об одной и той же функции, в случае когда мы для ее определения пользуемся несколькими произвольными кривыми (график) или несколькими произвольными формулами? Трудность эта является фактически иллюзорной и при правильном ознакомлении с понятием функции, исходящем из наглядных примеров соответствий (между множествами), задаваемых самими различными путями (вообще говоря, без графиков и формул), с ней можно не встретиться совсем.

Читайте также: