Распространение волн в упругих средах уравнение гармонической бегущей волны конспект

Обновлено: 03.07.2024

В этом семестре будем изучать волновые свойства упругих и электромагнитных волн, квантовые свойства электромагнитного излучения, элементы квантовой механики и атомной физики.

В первой части курса были рассмотрены простейшие случаи механических колебаний. При этом мы не интересовались процессами, происходящими в среде, окружающей колебательную систему. Сейчас мы обратим на это внимание.

Будем полагать, что имеем сплошную упругую среду, например, твердое тело, жидкости, газы. Для упругой среды характерно возникновение упругих деформаций при внешнем воздействии на нее. Эти деформации полностью исчезают после прекращения внешних воздействий.

Если в каком-либо месте упругой среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами эти колебания будут распространяться в среде с некоторой скоростью v.

Процесс распространения колебаний в среде называется волной. Иначе, возмущение, распространяющееся в пространстве (среде), называется волной.

Механические возмущения (деформации), распространяющиеся в упругой среде, называются упругими или механическими волнами.

Звуковыми или акустическими волнами называются упругие волны, обладающие частотами в пределах 16-20000 Гц. Волны с частотами меньше 16 Гц (инфразвук) и больше 20000 Гц (ультразвук) органами слуха человека не воспринимаются.

Упругие волны бывают продольныеипоперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространения волны.

Продольные волны могут возбуждаться в твердых, жидких и газообразных средах. Поперечные волны могут возникать только в твердых телах.

Отметим, что распространение упругих волн не связано с переносом вещества. Бегущие волны переносят энергию колебательного движения в направлении распространения волны.

Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими, т.е. описываются по закону синуса или косинуса. Часто гармоническую волну называют синусоидальной.

На рис.1 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси x, т.е. приведена зависимость между смещением S частиц среды и расстоянием х этих частиц от источника колебаний О для фиксированного момента времени t.

Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l. Длина волны равна тому расстоянию, на которое распространится гармоническая волна за время, равное периоду колебаний Т, т.е.

. (1)

Учитывая, что частота v = 1/T получаем

l = v / v. (2)

т.е. длина волны обратно пропорциональна частоте.

Уравнение такой волны в общем случае имеет вид

, (3)

Для характеристики волн используется волновое число

, (4)

где w = 2p/T = 2pv – циклическая, (круговая) частота.

С учетом (4) получим уравнение бегущей гармонической волны

, (5)

где А – амплитуда волны, – фаза волны, j₀– начальная фаза.

Основываясь на формуле Эйлера (), уравнение (5) можно записать в экспоненциальной (комплексной) форме

, (6)

где физический смысл имеет лишь действительная часть выражения (6). Такая форма представления волны существенно облегчает математический действия.

Упругие среды. Продольные и поперечные волны

Лекция 1. Волны в упругих средах

I. Волновые свойства упругих и электромагнитных волн

Издательство МГАПИ

УДК 53

Методическое пособие

Часть III

Физика

Беланов А. С.

Приборостроения и информатики

Утверждено Ученым советом МГАПИ

29.06.1998г. в качестве учебного пособия

Рецензент – доцент, к.ф.-м.н. Попова Т. В.

Учебное пособие предназначено для студентов МГАПИ,

изучающих физику в течении 4-х семестров

Ф и з и к а, ч а с т ь III

. (1)

Учитывая, что частота v = 1/T получаем

l = v / v. (2)

т.е. длина волны обратно пропорциональна частоте.

Уравнение такой волны в общем случае имеет вид

, (3)

Для характеристики волн используется волновое число

, (4)

где w = 2p/T = 2pv – циклическая, (круговая) частота.

С учетом (4) получим уравнение бегущей гармонической волны

, (5)

где А – амплитуда волны, – фаза волны, j₀– начальная фаза.

Основываясь на формуле Эйлера (), уравнение (5) можно записать в экспоненциальной (комплексной) форме

, (6)

Посмотрев данный видеоурок, учащиеся вспомнят, что называется механической волной и каковы её основные свойства. Мы также поговорим об особенностях распространения волн в упругих средах. Получим уравнение бегущей монохроматической волны. А также рассмотрим некоторые особенности отражения механических волн.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Распространение волн в упругих средах. Уравнение гармонической бегущей волны"

Всё время, пока существует волна, частицы среды совершают колебания около своих положений равновесия и смещаются от него не более чем на амплитуду. При этом различные частицы колеблются со сдвигом по фазе, за исключением тех, положения равновесия которых находятся друг от друга на расстоянии υТ.

Напомним, что геометрическое место точек среды, колеблющихся в одинаковых фазах, образует волновую поверхность.

Волновую поверхность, отделяющую колеблющиеся частицы среды от частиц, ещё не начавших колебаться, называют фронтом волны.

Как отмечалось нами ранее, возмущение, создаваемое источником волны, передаётся от одной точки среды к другой не мгновенно, а с определённой конечной скоростью. Скоростью распространения волны называется физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени.

Для указания направления распространения волн, используется понятие луча. Лучом мы будем называть линию, проведённую перпендикулярно волновому фронту в направлении распространения волны.

Ранее мы с вами показали, что при возбуждении волны происходит процесс распространения колебаний, но не перенос вещества. Следовательно, при распространении волн происходит перенос энергии упругой деформации и импульса без переноса вещества. При этом энергия волны в упругой среде состоит из кинетической энергии совершающих колебания частиц и потенциальной энергии упругой деформации среды.

На прошлом уроке мы с вами говорили о том, что расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны. Она равна тому расстоянию, на которое распространяется волна за период:

Так как период колебаний обратно пропорционален частоте колебаний, то скорость волны связана с частотой колебаний уравнением:

Выразим из этой формулы длину волны, а также воспользуемся связью частоты колебаний с их циклической частотой:

Отсюда видно, что при возникновении волн в среде их частота определяется частотой колебаний источника. А скорость распространения волны зависит от свойств среды. Поэтому волны одной и той же частоты имеют различную длину в разных средах.

Теперь давайте получим уравнение плоской волны, то есть волны, волновые поверхности которой представляют собой плоскости, перпендикулярные к направлению распространения волны.

Предположим, что вибратор совершает гармонические колебания, подчиняющиеся закону синуса (считаем, что начальная фаза колебаний равна нулю):

В записанной формуле s — это смещение колеблющейся точки от положения равновесия, а s_m — амплитуда колебаний.

В точках, отстоящих на расстоянии х от источника, колебания частиц среды волнового фронта будут также гармоническими, с той же частотой, но будут отставать от колебаний источника на время:

Эти точки также начнут также совершать гармонические колебания с той же частотой, но с запаздыванием на время τ. Колебания в точке х будут происходить с той же амплитудой, но с другой фазой:

Это и есть уравнение плоской бегущей монохроматической волны. При этом считают, что в процессе распространения волны её затуханием можно пренебречь. Из уравнения видно, что смещение любой точки среды из равновесного положения при прохождении волны является функцией двух переменных: времени и расстояния до равновесного положения точки среды.

Из этого уравнения также следует, что амплитуда плоской незатухающей волны в данной точке среды постоянна и равна амплитуде колебаний источника. Также видно, что любая точка среды совершает гармонические колебания, начальная фаза которых зависит от удаления данной точки от источника колебаний:

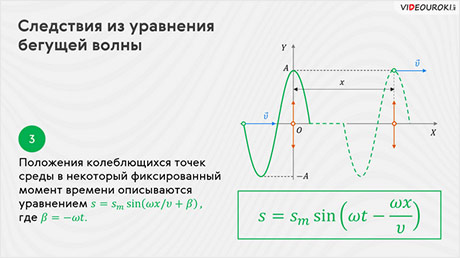
А положения колеблющихся точек среды в некоторый фиксированный момент времени описываются уравнением, которое вы сейчас видите на экране:

А теперь давайте с вами найдём разность фаз колебаний двух точек среды, находящихся на некотором расстоянии друг от друга:

Запишем уравнения, описывающие колебания этих двух точек:

Теперь найдём их разность фаз (напомним, что фазой колебания является аргументом периодической функции):

Перепишем полученное уравнение, воспользовавшись формулой, связывающей циклическую частоту с периодом колебаний:

В знаменателе формулы мы получили произведение периода колебаний и скорости волны, а это, как мы помним, есть длина волны:

Из последнего равенства следует, что если две точки находятся друг от друга на расстоянии длины волны, то разность фаз колебаний этих точек равна 2π, что соответствует данному нами ранее определению длины волны.

Теперь, для закрепления нового материала, давайте решим с вами задачу. Определите частоту звуковых колебаний в воздухе, если расстояние между двумя ближайшими точками волны, отличающимися по фазе на π, составляет 50 см. Для удобства будем считать, что скорость звука равна 340 м/с.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Бегущие волны. Уравнение волны. Волны в природе.

Бегущая волна – волна, которая при распространении в среде переносит энергию.

Уравнение бегущей волны Уравнение волны позволяет в любой момент времени определить смещение данной точки среды, в которой распространяется волна.

Уравнение гармонической бегущей волны можно записать в виде: s = smsin (ωt – kx), где k — волновое число Фазы колебаний двух точек, находящихся на расстоянии λ, отличаются на 2π, то есть колебания происходят в фазе.

Геометрическое место точек, в которых колебания происходят в одной фазе, называется волновой поверхностью. Луч — линия, перпендикулярная к волновой поверхности и к фронту волны. Направление луча указывает направление переноса энергии волной.

Фронт волны — геометрическое место точек, до которых дошло возмущение к данному моменту времени. Волновой фронт также является волновой поверхностью. Фронт волны отделяет часть пространства, в котором колебания уже есть, от части пространства, в которой колебания отсутствуют.

Плоская волна – это волна, волновые поверхности которой представляют собой совокупность параллельных друг другу плоскостей. Пример плоской волны – волна, возникающая в цилиндре с газом, при совершении колебаний поршнем.

Сферическая волна – это волна, волновые поверхности которой представляют собой совокупность концентрических сфер Примерами сферических волн служат волны, генерируемые точечным источником в однородной среде.

Задача 1 Определите скорость распространения υ поперечной волны в струне, площадь поперечного сечения которой S , если модуль силы ее натяжения F можно считать постоянным, а плотность вещества, из которого изготовлена струна равна ρ.

Задача 2 Определить частоту звуковых колебаний в стали, если расстояние между ближайшими различающимися по фазе на Δφ= 90° точками звуковой волны ℓ = 1,54 м. Скорость звуковых волн в стали v = 5000 м/с.

Задача 3 Плоская поперечная волна задана уравнением s = 2 • 10~4 sin (628 t - 0,3х), где s — смещение частицы в направлении, перпендикулярном направлению распространения волны, х — расстояние вдоль луча от источника колебаний. Определите частоту колебаний V, скорость распространения волны и, длину волны X и амплитуду колебаний скорости каждой частицы ит. Все величины в данном уравнении выражены в единицах СИ.

Задача 4 Точки, находящиеся на одном луче и удаленные от источника колебаний на L1=12м и L2=14,7м, колеблются с разностью фаз 3п/2 рад. Определите скорость распространения колебаний в данной среде, если период колебания источника 1мс.

Задача 5 Уравнение волны имеет вид x=sin 2,5πt. Найти смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии r = 20 м от источника колебаний, для момента времени t=1c после начала колебаний. Скорость распространения колебаний v=100 м/c

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 933 человека из 80 регионов

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

Курс добавлен 31.01.2022
Сейчас обучается 24 человека из 17 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 610 566 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

03.11.2017 11089
PPTX 900.3 кбайт
528 скачиваний
Рейтинг: 4 из 5
Оцените материал:

Настоящий материал опубликован пользователем Дежкина Лилия Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Рособрнадзор предложил дать возможность детям из ДНР и ЛНР поступать в вузы без сдачи ЕГЭ

Время чтения: 1 минута

Время чтения: 2 минуты

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Время чтения: 1 минута

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие

Время чтения: 15 минут

Академическая стипендия для вузов в 2023 году вырастет до 1 825 рублей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

. (1)

Учитывая, что частота v = 1/T получаем

l = v / v. (2)

т.е. длина волны обратно пропорциональна частоте.

Уравнение такой волны в общем случае имеет вид

, (3)

Для характеристики волн используется волновое число

, (4)

где w = 2p/T = 2pv – циклическая, (круговая) частота.

С учетом (4) получим уравнение бегущей гармонической волны

, (5)

где А – амплитуда волны, – фаза волны, j₀– начальная фаза.

Основываясь на формуле Эйлера ( ), уравнение (5) можно записать в экспоненциальной (комплексной) форме

, (6)

Фронт волны, волновые поверхности, фазовая скорость

Волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью(поверхностью постоянных фаз, фазовой поверхностью).

Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени – один.

Гармоническая бегущая волна (5) является плоской волной, т.к. ее волновые поверхности представляет собой совокупности плоскостей, параллельных друг другу и перпендикулярных оси х.

Уравнение гармонической сферической волны имеет вид

, (7)

где r – радиальная координата. При распространении волны в непоглощающей среде A(r) ~ 1/r.

Скорость v распространения гармонической волны называетсяфазовой скоростью. Она равна скорости перемещения волновой поверхности. Например, в случае плоской гармонической волны из условия следует, что

. (8)

Волновое уравнение

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных.

, (9)

где (10)

D – оператор Лапласа, v – фазовая скорость.

Решением уравнения (9) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (5), которая не зависит от координат y и z волновое уравнение принимает вид

. (11)

Соответствующей подстановкой можно убедится, что уравнению (11) удовлетворяет уравнение (5).

Читайте также: