Производная в строительстве конспект

Обновлено: 03.07.2024

Предмет исследования – производная.

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.

Ключевой и тематический вопросы данного реферата:

1. История возникновения производной.

2. Зачем изучать производные функций?

3. Где используются производные?

4. Применение производных в физике, химии, биологии и других науках.

В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.

Применение производной в различных областях науки

Из курса алгебры старших классов мы уже знаем, что производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.

Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Физический смысл производной: производная функции y = f ( x ) в точке x 0 – это скорость изменения функции f ( x ) в точке x 0 .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Геометрический смысл производной состоит в том, что производная функция в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .

Термин производная и современные обозначения y ' , f ' ввёл Ж.Лагранж в 1797г.

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;

Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.

Производная в алгебре:

1. Касательная к графику функции

Касательная к графику функции f, дифференцируемой в точке x о , - это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).

y = f (x о ) + f ′(x о ) (x – x о )

2. Поиск промежутков возрастания и убывания функции

Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции

Точку называют точкой максимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции

График функции , дифференцируемой на интервале , является на этом интервале выпуклым , если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

5. Поиск точек изгиба функции

Производная в физике:

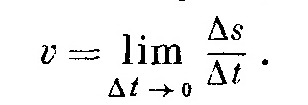
1. Скорость как производная пути

2. Ускорение как производная скорости a =

3. Скорость распада радиоактивных элементов = - λN

А так же в физике производную применяют для вычисления:

Скорости материальной точки

Мгновенной скорости как физический смысл производной

– мгновенная скорость, м/с
– перемещение тела, м ( если Δt→0 )
Δt – стремящийся к нулю интервал времени, с

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

Производная в химии:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ

§1. Геодезия

Если расстояние между точками B и C достаточно велико, то к найденному (с помощью угломерных инструментов) значению повышения точки B над точкой C прибавляют так называемую поправку на кривизну Земли: , где R – радиус Земли, l – длина горизонтальной проекции отрезка BC .

Докажем указанную выше формулу для поправки . Рассмотрим рис. 1, на котором штрихами изображена поверхность океана, точка O – центр Земли. Пусть точка C лежит на поверхности океана, а точка B принадлежит горизонтальной плоскости, проходящей через точку C . Так как в таком случае угол между лучом CB и горизонтальным направлением (оно определяется с помощью отвеса) равен нулю, то из точки C нам покажется, что точки B и C имеют одинаковую высоту. Согласившись с этим, мы допустим погрешность .

§2. Транспорт

В практике проектирования сети автомобильных дорог часто возникает необходимость устройства узла разветвления . Местоположение узла и взаимное расположение проходящих через него дорог определяется комплексом экономических и географических условий, но первый, предварительный этап решение этой задачи учитывает лишь затраты рабочего времени на перевозки, причём в качестве вспомогательной решается вначале следующая задача.

Каким должен быть угол примыкания (рис. 2) дороги (CE) к автомагистрали (AB), чтобы затраты времени на перевозки по маршруту AEC были наименьшими, если скорость движения автомобилей по магистрали планируется равной , а по объездной дороге – () ? Проведем через точку C перпендикуляр к прямой AB и обозначим длину отрезка CD через h , а длину отрезка AD через l . Тогда получим: , . Отсюда находим время движения автомобиля по маршруту AEC : . Так как точка A зафиксирована условно, определяя лишь направление движение по магистрали, то может изменяться в промежутке . Задача свелась к отысканию наименьшего значения в промежутке значения функции на указанном промежутке.

Найдём производную . Так как , то производная на рассматриваемом промежутке обращается в нуль лишь в одной точке , причём при и при . Это означает, что на промежутке функция t убывает, а на промежутке возрастает. Следовательно, рассматриваемая функция t при достигает наименьшего значения.

§3. Мелиорация

Площадь поперечного сечения канала называют его живым сечением , а длину границы такого сечения называют смоченным периметром канала. С помощью теоретических расчетов и эксперимента установлено, что из всех каналов с заданным живым сечением наибольшей пропускной способностью и одновременно наименьшей фильтрацией отличаются каналы с наименьшим смоченным периметром. Про такие каналы говорят, что они имеют гидравлически наивыгоднейший профиль .

В мелиоративной практике часто сооружаются каналы или лотки с поперечным сечением в форме прямоугольника, треугольника, трапеции и сегмента круга. Поэтому представляет интерес расчет гидравлически наивыгоднейшого профиля для каналов такой формы.

При каком отношении глубины к ширине канал прямоугольного сечения имеет гидравлически наивыгоднейший профиль? Пусть x – ширина канала, – его живое сечение. Тогда глубина канала , а его смоченный периметр (рис. 3): .

Требуется найти наименьшее значение функции на промежутке . Найдем производную: . Так как , при и при , то функция в точке достигает наименьшего значения.

Итак, ширина канала в рассматриваемом случае должна быть , глубина , а искомое отношение равно 0,5.

Сечение канала – равнобедренная трапеция (рис. 4) с углом откоса таким, что . При каком отношении ширины дна канала к его глубине он имеет гидравлически наивыгоднейший профиль? Пусть ширина дна канала b, а его глубина h . Тогда , , (1) , . Из (1) получаем, что , а значит (0 h ). С помощью производной находим, что функция достигает наименьшего значения на промежутке при .

Сечение канала – сегмент (рис. 5) . Каким должен быть центральный угол , чтобы канал имел гидравлически наивыгоднейший профиль? Пусть R – радиус круга. Живое сечение канала найдем как разность площадей сектора и треугольника: . Отсюда получаем, что , и значит, смоченный периметр .

Исследуем более простую функцию . При имеем . Так как и на рассматриваемом интервале, то производная на определена и отрицательна. Поэтому функция f , а значит, и убывает на . В силу непрерывности функции на промежутке заключаем, что убывает и на таком промежутке. Следовательно, функция достигает наименьшего значения при . В сечении канала должен быть полукруг.

§4. Строительство

При монтаже промышленных и сельскохозяйственных зданий небольшой высоты широко используются автомобильные краны. Для правильного выбора крана необходимо знать многие исходные данные о сооружаемом объекте. В частности, габаритные данные объекта позволяют заранее определить требуемую длину стрелы крана. Рассмотрим эту задачу.

Вывести формулу для определения длины стрелы автомобильного крана, с помощью которого можно поставить здание H и ширины 2l с плоской крышей. Так как автомобильный кран может перемещаться вокруг всего здания, то крюк его крана достанет до любой точки здания, если он достает (рис. 6) до середины крыши (имеется в виду середина по ширине).

Рассмотрим кран, который, находясь в точке O , подает деталь на середину крыши. Пусть угол наклона стрелы при этом составляет . Тогда ; , где – высота подвеса стрелы крана. В таком случае (2) .

Из формулы (2) видно, что для совершения указанной работы краном, установленным в другой точке (ближе к зданию или дальше от него), потребуется кран с другой длиной стрелы, поскольку при таком перемещении меняется угол . Определим наивыгоднейшее место установки крана, т.е. такое место, с которого заданная работа может быть выполнена краном с наименьшей длиной стрелы. Для этого достаточно определить, при каком из промежутка функции l принимает наименьшее значение.

Найдем производную функции l : .

Рассуждая теперь так же, как и при решении задачи из §2, находим, что функция l достигает наименьшего значения при (3) .

Найдя из формулы (3) значение и подставив в формулу (2), мы получим наименьшее возможное значение длины стрелы. Эти формулы и используются на практике.

§5. Деревообработка

Важное народнохозяйственное значение имеет рациональный раскрой древесины. Комплексное решение таких задач требует применение довольно глубоких методов классической и современной математики. Однако отдельные задачи такого рода можно решить, используя только производную.

На лесопильных рамах (они предназначены для продольного пиления) бревна часто распиливают на квадратный брус и четыре доски (рис. 7) с максимально возможной площадью поперечного сечения. Какой должна быть расстановка пил для такой распиловки? Из рис. 7 видно, что для ответа на вопрос задачи достаточно определить толщину выпиливаемых досок. Так как сторона квадрата, вписанного в окружность радиуса r , равна , то . Пусть толщина доски . Тогда ее ширина, а площадь поперечного сечения .

Требуется узнать, при каком x из отрезка функция S достигает наибольшего значения. Найдем производную: . Критическая точка . Так как , а , то доски толщиной 0,1 d имеют наибольшую площадь поперечного сечения.

Материал с практическим содержанием, решение задач с профессиональной направленностью можно использовать на урокахв группах автомехаников.

Предварительный просмотр:

Областное бюджетное профессиональное образовательное учреждение

Преподаватель Власова В.Е.

Методическая цель: Методика активизации познавательной деятельности обучающихся в ходе решения профессиональных задач на уроках математики.

Тип урока: урок обобщения, систематизации знаний, умений и навыков.

Вид урока: деловая игра

Методы обучения: словесные, наглядные, практические, проблемно-поисковые, самостоятельная работа.

Межпредметные связи: физика, правила безопасности дорожного движения, техническое обслуживание и ремонт автотранспорта, охрана труда.

1. Организационный момент 1 мин

2. Мотивация учебной деятельности 2 мин

3. Актуализация знаний и закрепление 39 мин

самостоятельная работа. Выполнение расчётных заданий автотранспортных и строительных организаций г. Курска;
защита студентами расчётных заданий;
решение задачи на нахождение наименьшего значения площади заправочного модуля;
решение задачи на определение траектории движения гоночного автомобиля.

4. Домашнее задание 1 мин

5. Подведение итогов 2 мин

1. Организационный момент

Девизом нашей встречи мне хотелось бы взять слова великого русского математика Николая Ивановича Лобачевского, которые вам и предстоит доказать в течение рабочего дня “. нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира. ”

Начнем с производственного совещания. Руководители отделов доложите какие направления в теме производная вы рассматривали.

Что такое производная?

Каков геометрический смысл производной?

Каков физический смысл производной?

Для чего используется производная?

Найти производную функций.

3) f(x) = cos 5x - tgx

4) f(x) =sin 7x +3ctgx

Найти значение производной в точке

5) f(x) = 6 sinx , х = π

6) f(x) = 4Х 5 - 7, х = -1

7) f(x) = 6 -9х, х = 9

Задание . Установите соответствие с помощью стрелок между началом и концом утверждения. Ниже в таблице под номером вопроса поставьте только выделенную букву. У вас должно получиться ключевое слово.

1.Если точка х является точкой экстремума функции и в этой точке существует производная, то

точка, в которо й производная равна нулю или ее не существует.

2.Пусть точка движется по закону

функция f(x) у б ывает на данном интервале

3.Критической точкой функции f(x) на отрезке называется

она равна ну л ю.

4.Если производная функции меньше нуля в каждой точке интервала, то

х точка макс и мума

5.Если в точке х производная меняет знак с минуса на плюс, то

функ ц ия f(x) возрастает на интервале

6.Если в точке х производная меняет знак с плюса на минус, то

первая производная опр е деляет скорость точки, а вторая производная определяет ускорение точки в момент времени t.

7.Если производная функции больше нуля в каждой точке интервала, то

х точка ми н имума.

Ответ: Лейбниц (годы жизни 1646-1716)

В научно-расчётный центр пришли письма от различных организаций, которые хотят получить ответы и расчёты на интересующие их вопросы. Вы должны дать полные, обоснованные ответы и расчёты, которые потом будут отправлены заказчикам. Затем вам предстоит защитить свои расчеты.

На трассе Курск- Воронеж произошла авария. Для выяснения степени виновности водителя нам необходимо знать:

а) в течение какого времени осуществлялось торможение до полной остановки машины?

б) сколько метров двигалась машина с начала торможения?

в) чему равно ускорение в любой момент времени?

Нами установлено, что тормозной путь определяется по формуле:

S (t) =120t-10t 3 , где t (c), S (м)

С уважением сотрудники ГИБДД г. Курска .

Просим Вас помочь в решении следующей проблемы. Нам необходимо провести мост через реку. Мост имеет форму параболы у(х) = рх 2 . Каким надо сделать уклон насыпи к мосту, чтобы переход с моста на шоссе был плавным? Пролет моста имеет длину L=20 м., стрела провеса f=0,5 м. Предлагаем чертёж нашей работы:

Письмо из компании Технорессурс

Специалисты ремонтной мастерской по договору должны еженедельно изготавливать не менее 40деталей. Производственные мощности мастерской таковы, что максимально можно выпускать в неделю 80 деталей.

При каком объеме производства удельные затраты будут наибольшими и наименьшими, если функция затрат имеет вид: К=-х 3 +98х 2 +200х. Удельные затраты составляют .

В отдел охраны труда обращается руководитель ремонтной мастерской

Объем продукции u(t), произведенный бригадой рабочих, может быть описан уравнением u (t) = - 5/6 t 3 + 15/2 t 2 + 100 t + 50 (ед.), 1 ≤ t ≤ 8, где t - рабочее время в часах.

Просим Вас найти производительность труда через час после начала работы и за час до окончания. исследовать ее и построить график изменения производительности труда.

Просим Вас рассчитать тормозной путь и расход горючего в следующих задачах.

Автомобиль приближается к мосту со скоростью 72 км/ч. Перед мостом висит дорожный знак "40км/ч". За 7 сек до въезда на мост, водитель нажал на педаль тормоза. С разрешенной ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой s=20t-t²

Расход горючего легкового автомобиля (литров на 100 км) в зависимости от скорости Х км/час при движении на четвертой передаче приблизительно описывается функцией f(х)= 0,0017Х 2 -0,18Х +15,2, х >30км/час. При какой скорости расход горючего будет наименьшим?

С уважением старший мастер автотехнического колледжа

Защита решений у доски

1 .Для хранения горючих материалов в колледже требуется изготовить мобильный заправочный модуль в виде прямоугольного параллелепипеда с квадратным основанием. Объем 512 литров. С целью экономии материала, идущего на изготовление емкостей, просим Вас рассчитать, при какой стороне основания параллелепипеда, площадь поверхности будет наименьшей?

2 .На графике представлена зависимость скорости гоночного автомобиля от времени. Определить по какой траектории двигался этот гоночный автомобиль.

К следующему рабочему дню вам необходимо иметь следующие документы:

На пять – решить любые 4 задачи
На четыре – решить любые 3 задачи
На три – решить любые 2 задачи
Дополнительно можно подобрать или составить задачу на применение производной

Тело массой 2 кг движется прямолинейно по закону х (t) = t 2 +t+1. Координата х измеряется в сантиметрах, время t – в секундах. Найдите: а) действующую силу; б) кинетическую энергию (Е) тела через 2 с после начала движения.

Заготовленной плиткой нужно облицевать 6000 кв. м боковых стенок и дна желоба прямоугольного поперечного сечения длиной 1000 м. Каковы должны быть размеры сечения, чтобы пропускная способность желоба была наибольшей?

Необходимо построить открытый желоб прямоугольного сечения для стока воды. Длина периметра поперечного сечения желоба должна равняться 6 м. Какой высоты должны быть стенки желоба, чтобы получился максимальный слив?

Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200 м, и площадь ее при этом оказалась наибольшей. Каковы размеры площадки?

Пусть дана функция m=m(t), где m – количество некоторого вещества, вступившего в химическую реакцию к моменту времени t. Приращению времени t будет соответствовать приращение m величины m. Отношение – средняя скорость реакции за промежуток времени t. Предел этого отношения при t –> 0, т.е. lim m/t есть скорость химической реакции в данный момент времени t.

В данной разработке представлен материал, позволяющий закрепить и развить знания учащихся по теме "Производная и ее применнение" в 11 классе.

Муниципальное бюджетное общеобразовательное учреждение

ПРОЕКТНОЕ ЗАДАНИЕ

Внеклассная работа по математике.

Работа выполнена слушателем годичных курсов

повышения квалификации - учителем математики

Голубовой Викторией Витальевной

Содержание работы

ПРЕДИСЛОВИЕ К ВЫПОЛНЕННОЙ РАБОТЕ 3

ВНЕКЛАССНАЯ РАБОТА ПО МАТЕМАТИКЕ 4

ПЛАН КОНФЕРЕНЦИИ 5

1. Вступительное слово 6

2. Задачи на оптимизацию. 7

3. Применение производной в строительстве. 8

4. Производная и транспорт. 8

5. Производная помогает мелиорации. 9

6. Космос и производная. 10

7. Случай в заповеднике. 12

Рекомендуемая литература 13

ПРЕДИСЛОВИЕ К ВЫПОЛНЕННОЙ РАБОТЕ

Надо ли учить школьников решать прикладные задачи с физическим, техническим, экономическим содержанием?

Если вообще отказаться от задач с реальным предметным содержанием, то ученик не сможет решить ничего, кроме теоретических упражнений.

Современная педагогика видит три цели математического образования. Первая – общеобразовательная. Без математики невозможно понять ряд других предметов, нельзя продолжить образование в вузе по многим специальностям. Ядро математического знания давно стало общечеловеческой культурной ценностью.

Вторая цель – прикладная. Школьник, как правило, еще не знает, чем он будет заниматься, поэтому у учителя остается одна реальная возможность – научить детей принципам математического моделирования каких-либо реальных процессов.

Третья цель – воспитательная. Математика развивает логическое, пространственное и алгоритмическое мышление; формирует такие качества, как трудолюбие, настойчивость, усидчивость; учит ценить красоту мысли. Но еще важнее другое: математика – это мировоззрение. Человек, владеющий математическим методами исследования, иначе подходит к жизненным проблемам, иначе смотрит на мир.

Прикладная направленность преподавания математики связана со всеми тремя названными целями: с общеобразовательной (легче учить другие предметы), с прикладной ( будущий специалист еще в школе получает необходимые навыки прикладного математического исследования), с воспитательной ( мир един, и именно в содружестве с другими науками математика формирует у ребенка основы научной картины мира)

ВНЕКЛАССНАЯ РАБОТА ПО МАТЕМАТИКЕ

Чтобы достичь хороших результатов по математике, необходимо осуществлять хорошо спланированную внеклассную работу по предмету. При этом очень важно, чтобы работа, осуществляемая на уроках, и работа, проводимая во внеурочное время, представляли собой единое целое, были взаимосвязаны, имели логическое продолжение. Умело организованная, систематическая внеклассная работа даёт возможность развивать и углублять профессиональные интересы и склонности учащихся; значительно обогащать их знания о различных областях приложения математики, её роли в производстве; способствует развитию творческих способностей учащихся, усиливает их интерес к математике.

Для осуществления внеклассной работы можно использовать самые разнообразные формы. Со старшеклассниками можно готовить и проводить интересные вечера, конференции, посвящённые различным приложениям математики.

Оформление зала:

Портреты: Исаак Ньютон, Готфрид Вильгельм Лейбниц, Леонид Витальевич Канторович

Алгоритм решения задач на оптимизацию:

Найти критические точки.

Вычислить значение функции в каждой критической точке.

Вычислить значение функции на концах отрезка.

Из полученных чисел выбрать наибольшее ( наименьшее).

Этапы решения прикладных задач:

Построение математической модели.

Решение внутри модели.

Интерпретация полученного результата.

Вступительное слово учителя.

Задачи на оптимизацию.

Применение производной в строительстве.

Производная и транспорт.

Производная помогает мелиорации.

Космос и производная.

Случай в заповеднике.

Ниже приводится некоторый материал к каждому пункту плана конференции, который может быть использован как учителем так и учащимися.

1. Вступительное слово

Сегодня на конференции мы с вами с некоторыми видами трудовой деятельности в которых используется важное понятие математики – производная.

И в наше время, как и в далёком прошлом, практика выдвигает перед математикой сложные задачи. Именно в этом причина современного бурного развития математики, появление многих её новых областей, позволяющих глубоко изучать явления окружающего нас мира и решать конкретные практические задачи. В настоящее время математические методы становятся необходимым орудием расчета буквально всех важнейших процессов в народном хозяйстве. Без знаний математики невозможно представить себе работу многих специалистов: инженеров, экономистов, организаторов производства, агрономов, квалифицированных рабочих.

Когда-то королева Англии пригласила к себе великого Ньютона. Она попросила побывать на монетном дворе и подсчитать, сколько дополнительных помещений, станков и рабочих нужно добавить, чтобы выпускать в 1,5 раза больше монет. Ньютон, вникая в производство, провёл на монетном дворе полдня. Остальное время суток он просидел за письменным столом, занимаясь расчетами. Утром он предложил королеве следующее решение: можно, не производя никаких добавлений, увеличить выпуск монет в два раза. Для этого достаточно произвести лишь некоторые изменения в организации производства: переставить станки, по-иному распределить рабочих, изменить последовательность операций.

2. Задачи на оптимизацию.

За разработку общих методов решения задач на наименьшее и наибольшее значение, или, как их еще называют, задач на оптимизацию, русский математик Леонид Витальевич Канторович в 1975 году стал лауреатом Нобелевской премии.

Следует различать два вида задач на оптимизацию. В задачах первого вида улучшение достигается за счет коренных качественных изменений (выбор новых конструктивных решений, переход на новую технологию изготовления данной продукции). В задачах второго рода качественная сторона дела остается неизменной, но меняются количественные показатели, например, размеры прибора, соотношение веществ, используемых для химической реакции, начальная скорость ракеты. С математической тоски зрения в этих задачах отыскивается наибольшее и наименьшее значения функций. Один из способов решения таких задач основан на применении производной.

3. Применение производной в строительстве.

Пользуясь обозначениями, указанными на

чертеже, получим формулу, выражающую длину

стрелы крана L=+, где α- угол наклона

стрелы. Из формулы видно, длина стрелы крана

зависит от угла α, который меняется изменением

положения крана. Выгодного положение

крана является такое место, с которого заданная

работа может быть выполнена краном с

наименьшей длиной стрелы.

В результате отыскание выгодного положения крана сводится к нахождению наименьшего значения функции L=+, на промежутке (0; ). С помощью производной установим, что наименьшее значение длины стрелы получается при α =

arctg. Эта формула используется на практике.

4. Производная и транспорт.

Выберем систему координат так, как показано на рисунке.

Уравнение параболы АОВ будем искать в виде у = ах, где х и у- координаты произвольной точки параболы, а - параметр. Рассмотрим точку А (х,С). Так как точка А лежит на параболе АОВ, то С = ах(1). По условию m = 2ах(2), где 2ах= у(х). Выразив х из уравнения (2) и подставив в равенство (1), получим выражение параметра а = m/4С. В результате уравнение параболы АОВ примет вид: у = x.

5. Производная помогает мелиорации.

В мелиоративной практике часто сооружаются каналы с поперечным сечением в форме прямоугольника, трапеции и сегмента круга. Рассмотрим некоторые характеристики канала: живое сечение, смоченный периметр, которые обозначаются соответственно через ω, λ. Положим для простоты, что канал полностью заполнен водой. Живое сечение – площадь поперечного сечения. Смоченный периметр – длина границы соприкосновения потока со стенками канала.

Пользуясь обозначениями, принятыми на чертеже, получим равенство λ=Rα, ω=(α-sinα ), где ω – задано. Поскольку λ зависит от двух переменных, то из второго равенства выразим R и подставим в первое, получим функцию, зависящую от α: λ = . С помощью производной установим, что функция λ принимает наименьшее значение при α = π, т. е. в сечении канала должен быть полукруг.

6. Космос и производная.

Дифференциальное и интегральное исчисления являются теоретическим базисом космонавтики. Без понятий производная, интеграл, решение дифференциального уравнения были бы невозможны расчеты прочности корпуса ракеты – носителя, тех скоростей, которые необходимо придавать космической станции, чтобы она могла выполнить порученное ей задание; невозможно осуществить управление ее полетом. Рассмотрим одну из задач такого рода: «Ракета – носитель движется прямолинейно по закону

S = ν₀t +

Через время t после начала движения от нее отделяется для выполнения задания пилотируемый аппарат, который продолжает двигаться по инерции.

Рассмотрим геометрическую интерпретацию задачи (смотри рисунок). Обозначим скорость пилотируемого аппарата V. По условию задачи

V(t) = S´(t), с этой скоростью пилотируемый аппарат будет двигаться до момента ее изменения. В этом случаи графиком закона его движения является касательная, проведенная к параболе в точке (t, S(t)). В момент t V(t)=S´(t) . Поэтому в некоторый момент t t аппарату необходимо придать скорость S´(t) и, начиная с момента t до t момента, графиком его движения является касательная, проведенная к параболе в точке (t, S(t)). Легко видеть, что момент t будет найден, если будет найдена точка пересечения касательных. Найдем уравнения касательных, проведенных к параболе соответственно в точках: (t, S(t)), (t, S(t)).

S = S (t) + S´(t)(t - t) и S = S (t) + S´(t)(t - t), где S´(t) = V + at.

Найдем точку пересечения касательных:

S (t) + (V + at)( t - t) = S (t) +(V + at)(t - t) или

V t+ + (V + at)( t - t) = V t+ + +(V + at)(t - t).

Отсюда: t = (t+ t)/2. Таким образом, для того, чтобы пилотируемый аппарат догнал ракету – носитель, ему нужно придать скорость V= V + at в момент времени : t = (t+ t)/2.

7. Случай в заповеднике.

Мы увидели сегодня как широко применяется производная. Какие профессии требуют хорошего знания математики. И поэтому, если вы хотите участвовать в большой жизни, то пополняйте свою голову математикой, пока есть к тому возможность.

Читайте также: