Конспект урока четность нечетность периодичность тригонометрических функций 11 класс алимов
Обновлено: 02.07.2024
Презентация содержит теоретический материал по теме, примеры решения задач, задания для самостоятельносй работы. С успехом была применена для "перевернутого урока".
| Вложение | Размер |
|---|---|
| chetnost_periodicynost_11.ppt | 1.25 МБ |
Предварительный просмотр:
Подписи к слайдам:
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ, ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ КУЗЬМИНА НАДЕЖДА АЛЕКСАНДРОВНА ГБОУ ЛИЦЕЙ №387 ИМЕНИ Н.В. БЕЛОУСОВА КИРОВСКОГО РАЙОНА САНКТ-ПЕТЕРБУРГА
ПРОВЕРЬ СЕБЯ Функция Область определения D(y) Множество значений E(y) y=sin x y=cos x y=tg x y=ctg x R R R R
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ, ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
ЧЕТНЫЕ ФУНКЦИИ Функция y = f(x) называется четной, если для любого х из области определения функции - x тоже принадлежит области определения данной функции и верно равенство f(-x) = f(x). Чтобы узнать является ли функция четной нужно 1. найти D(y) и убедиться, что она симметрична относительно начала координат 2. в функцию f(x) вместо переменной х поставить переменную( –x ) и получить первоначальную функцию .
ЧЕТНЫЕ ФУНКЦИИ Задача 1. Является ли четной функция f(x) = 3x 2 + 2 Решение: D(Y)=R – симметрична относительно (0;0) f (-x) = 3(-x) 2 + 2 = 3x 2 + 2 = f(x) – функция четная
ЧЕТНЫЕ ФУНКЦИИ А) f(x) = 2x 4 - 3x 2 Б) f (x) = x 3 - 2x 2 Решение: А) D(y) : R f( - x) = 2(-x) 4 – 3(-x) 2 = 2x4 - 3x2 = f(x) – четная Б) D(y) : R f ( - x) = (- x ) 3 – 2 (- x ) 2 = – x3 – 2x2 не является ни четной, ни нечетной Являются ли данные функции четными
ГРАФИК ЧЕТНОЙ ФУНКЦИИ График четной функции симметричен относительно оси ординат (ось ОУ).
НЕЧЕТНЫЕ ФУНКЦИИ Функция y = f(x) называется нечетной, если для любого х из - x тоже принадлежит области определения данной функции и области определения функции верно равенство f(-x) = - f(x). Чтобы узнать является ли функция нечетной нужно 1. найти D(y) и убедиться, что она симметрична относительно начала координат 2. в функцию f(x) вместо переменной х поставить переменную ( – x ) и получить первоначальную функцию с противоположными знаками .
НЕЧЕТНЫЕ ФУНКЦИИ Задача 2. Является ли нечетной функция f(x) = 3x 3 + х Решение: D(y) : R f (-x) = 3(-x) 3 + (-х) = - 3x 3 - х = -( 3x 3 + х)= = - f(x) – функция нечетная
НЕЧЕТНЫЕ ФУНКЦИИ Решение: А) D(y) : R f ( - x) = 2(-x) 4 + 3(-x) = = 2x 4 - 3x - не является ни четной, ни нечетной Б) D(y) : R f ( - x) = (- x ) 3 – 2 (- x ) = – x 3 + 2x нечетная Являются ли данные функции нечетными
ГРАФИК НЕЧЕТНОЙ ФУНКЦИИ График нечетной функции симметричен относительно начала координат.
ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ Функции могут быть как четными, нечетными , так и ни четными, ни нечетными.
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Для любого значения x верны равенства : sin(-x) = -sin x cos(-x) = cos x tg(-x) = -tg x ctg(-x) = -ctg x Следовательно : y = sin x , у = tg x , у = ctg x – нечетные функции y= cos x – четная функция
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Задача 4. Выяснить, является ли функция y = 2 + Sin2 x четной или нечетной. Решение : ООФ: R y(-x) = 2 + sin 2 (-x) = 2 + (-sin x) 2 = =2 + sin 2 x = y(x) y = 2 + sin 2 x – четная функция .
Четность и нечетность тригонометрических функций
Разбейте функции на три группы: четные, нечетные, не являются ни четными, ни нечетными
Ответы: четные нечетные ни чет., ни нечет. 1 2 5 4 3 7 9 6 15 10 8 11 14 12 13
ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
ПЕРИОДИЧНОСТЬ Для любого значения x верны равенства : sin (x + 2 π ) = sin x cos (x + 2 π ) = cos х Следовательно, значения синуса и косинуса периодически повторяются при изменении аргумента на 2 π . Такие функции называются периодическими с периодом 2 π .
ОПРЕДЕЛЕНИЕ Функция f(x) называется периодической , если существует такое число T ≠ 0 , что для любого х из области определения этой функции х+Т и х-Т тоже принадлежат области определения этой функции и выполняется равенство f(x – T) = f(x) = f(x + T). Число T называется периодом функции f(x).
ПОКАЖЕМ, ЧТО ЧИСЛО 2 Π ЯВЛЯЕТСЯ НАИМЕНЬШИМ ПОЛОЖИТЕЛЬНЫМ ПЕРИОДОМ ФУНКЦИИ Y = COS X. Пусть Т › 0 – период косинуса, т.е. для любого x выполняется равенство Cos (x + T) = Cos x. Положив x = 0 , получим Cos T = 1. Отсюда T = 2 π k, k є Ζ . Так как Т › 0, то Т может принимать значения 2 π , 4 π , 6 π , …, и поэтому период не может быть меньше 2 π . АНАЛОГИЧНО МОЖНО ДОКАЗАТЬ, ЧТО НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = SIN X ТАКЖЕ РАВЕН 2 Π
ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Задача 6 . Доказать, что f(x) = Sin 3x – периодическая функция с периодом ( 2 π ) /3. Доказательство : Данная функция определена для всех x є R , поэтому достаточно показать, что для любого x верно равенство f(x + T) = f(x) . f(x + (2 π )/3) = Sin 3(x + (2 π )/3) = = Sin (3x + 2 π ) = Sin 3x = f(x)
ПОКАЖЕМ, ЧТО ФУНКЦИЯ Y= TG X ЯВЛЯЕТСЯ ПЕРИОДИЧЕСКОЙ С ПЕРИОДОМ Π . Если x принадлежит области определения этой функции, т.е. x ≠ - π /2 + π n, n є Ζ , то по формулам приведения получаем tg(x – π ) = -tg( π – x) = -(-tg x) = tg x tg(x + π ) = tg x Таким обтазом, tg(x – π ) = tg x = tg(x + π ). Следовательно, π – период функции у = tg x.
ПОКАЖЕМ, ЧТО Π – НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = TG X. Пусть Т – период тангенса, тогда tg(x + T) = tg x, откуда при x = 0 получаем tg T = 0, T = k π , k є Ζ . Так как наименьшее целое положительное k равно 1, то π – наименьший положительный период функции y = tg x.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Тип урока: урок изучения нового.
Учебная задача: формирование представлений о нечетной и четной функции,
о периодической функции, о периоде функции, о наименьшем положительном периоде.
По окончании урока ученик:
- определение области определения и множества значений функции, в том числе тригонометрических функций;
- определение четности и нечетности функции;
- определение периодичности тригонометрических функций;
- свойства тригонометрических функций.
- находить область определения и область значений тригонометрических функций;
- находить период тригонометрических функций, исследовать их на четность и нечетность;
- находить нули тригонометрических функций;
- находить промежутки постоянных знаков.
- что периодические функции имеют бесконечно много периодов.
Методы обучения: эвристическая беседа, репродуктивный, частично – поисковые.
Форма обучения: фронтальная.
Средства обучения: традиционные, канва-таблица, презентация.
Мотивационно - ориентировочная часть (15 мин)
Содержательная часть (25 мин)
Рефлексивно - оценочная часть (5 минут)
Учащимся дается предварительное домашнее задание: указать область определения и множество значений функций y = cos x , y = sin x , y = tg x и
y = ctg x , проверить на четность/нечетность, указать промежутки знакопостоянства.
Проверим домашнее задание.
Какова область определения функции y = cos x ?
Запишем в канву-таблицу.
Каково множество значений функции y = cos x ?
Запишем в канву-таблицу.
Функция y = cos x является четной или нечетной?
Запишите в канву-таблицу.
При каких значениях х функция у=cos x принимает значение, равное 0?
Запишем в канву-таблицу.
При каких значениях х функция принимает положительные значения?
Запишем в канву-таблицу.
Какова область определения функции y = sin x ?
Запишем в канву-таблицу.
Каково множество значений этой функции?
Запишем в канву-таблицу.
Следующее свойство – четность/нечетность.
Какой является функция y = sin x ?
Запишем в канву-таблицу.
При каких значениях х функция у=s in x принимает значение, равное 0?
Запишем в канву-таблицу.
При каких значениях х функция принимает положительные значения?
Запишем в канву-таблицу.
Какова область определения функции y = tg x ?
Каково множество значений этой функции?
Четной или нечетной является данная функция?
Запишите в канву-таблицу.
При каких значениях х функция принимает значение, равное 0?
Запишем в канву-таблицу.
Какова область определения функции y = c tgx ?
Запишем в канву-таблицу.
Каково множество значений данной функции?
Запишем в канву-таблицу.
Какой является данная функция, чётной или нет?
Запишите в канву-таблицу.
При каких значениях х функция принимает значение, равное 0?
Запишем в канву-таблицу.
Функции y = cos x , y = sin x , y = tg x , y = ctg x называются тригонометрическими функциями.
Тригонометрическими функциями описываются многие процессы реальной действительности, которые периодически повторяются по истечении некоторого промежутка времени. Периодически, с периодом в 1 год, меняется расстояние Земли от Солнца, с периодом в 1 лунный месяц меняются фазы Луны и т.д.
Постановка учебной задачи
Итак, мы рассмотрели некоторые свойства тригонометрических функций, но эти функции обладают еще одним важным свойством, о котором мы ранее не говорили, т. к. не было соответствующих функций, которые это свойство иллюстрировали - это свойство периодичности.
Область определения функции y = cos x – все действительные числа.
Для любого действительного числа х можно указать соответствующую точку на единичной окружности, полученную поворотом точки (1,0) на угол х радиан, а следовательно ее абсциссу, т.е. косинус числа х.
Д ( у ): R
Множеством значений функции y = cos x является отрезок –1 £ у £ 1.
Т.к. абсциссы точек единичной окружности пробегают именно этот промежуток.
Е ( у ): [−1;1]
Функция y = cos x четная.
Область определения функции симметрична относительно начала координат и для любого значения х верно равенство cos (- x )= cos x .
, т.е. четная функция.
с os x =0, х = p /2+ p n , n Î Z .
с os x =0, х = p /2+ p n , n Î Z
- p / 2 + 2 p n x p / 2 + 2 p n , n Î Z .
p/2+ 2 p n x 3 p/ 2 + 2 p n , n Î Z .
Область определения y = sin x – все действительные числа.
Для любого действительного числа х можно указать соответствующую точку на единичной окружности, полученную поворотом точки (1,0) на угол х радиан, а, следовательно, ее ординату, т.е. синус числа х .
Д ( у ): R
Множеством значений функции y = sin x является отрезок –1 £ у £ 1.
Т.к. ординаты точек единичной окружности пробегают именно этот промежуток.
Е ( у ): [−1;1]
Функция y = sin x нечетная.
Область определения функции симметрична относительно начала координат и для любого значения х R верно равенство sin (- x )= - sin x .
, т.е. нечетная функция
sin x =0, x=, nZ .
sin x =0, x=, nZ
2 p n x p + 2 p n , n Î Z .
- p+ 2 p n x n , n Î Z .
- p / 2 + p n x π/ 2 + p n , n Î Z .
y = tg x – нечетная.
tgx =0 при x = πn , nZ
p n x p / 2 + p n , n Î Z .
Отрицательные при: - p/ 2 +p n x
n , n Î Z .
p n x π+ p n , n Î Z .
у= ctgx – нечетная.
ctg x =0 при х = p /2+ p n , n Î Z ;
p n x p / 2 + p n , n Î Z .
p/ 2 +p n x n , n Î Z .
II. Содержательная часть
Формулируется определение: функция f ( x ) называется периодической, если существует такое число T 0, что для любого x из области определения этой функции выполняется равенство f ( x - T )= f ( x )= f ( x + T ). Число Т называется периодом функции f ( x ).
Примером периодической нетригонометрической функции может служить функция у = < х >, которая каждому числу х ставит в соответствие его дробную часть.
Например, = 0,56; = 0,01 и т.д. Если к произвольному числу х прибавить 1, то изменится лишь целая часть этого числа; дробная же часть останется прежней. Следовательно, < х + 1> = < х > и потому функция у = < х > является периодической с периодом 1.
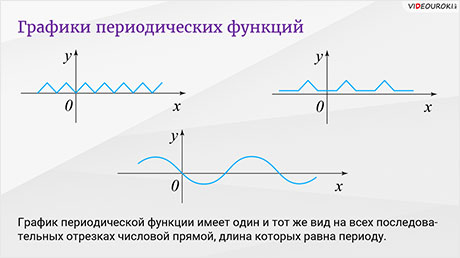
Из равенства f ( x + T ) = f ( x ) следует, что все значения функции у = f ( x ) повторяются с периодом T. Это находит свое отражение и в графическом изображении периодических функций.
На рисунке представлен график функции у = < х >. Периодичность функции у = < х > обусловливает то, что график ее в интервале [0, 1] имеет ту же самую форму, что и в интервалах [1, 2], [2, 3] и т. д.
Если Т – период функции f ( x ), то 2 Т , 3 T , 4 Т и т. д. – также периоды этой функции.
f ( x + 2 T ) = f [( x + T ) + Т ] = f ( x + T ) = f ( x ),
f ( x + 3 T ) = f [( x + 2 T ) + Т ] = f ( x + 2 T ) = f ( x )
и т. д. Кроме того, периодом функции f ( x ) можно считать и любое из чисел: – Т , – 2 T , – 3 Т и т. д. В самом деле,
f ( x – Т ) = f [( x – Т ) + Т ] = f ( x ),
f ( x – 2 Т ) = f [( x – 2 Т ) + 2 Т ] = f ( x ) и т. д. Итак, если число Т есть период функции f ( x ), то при любом целом п число п Т также период этой функции. Поэтому всякая периодическая функция имеет бесконечное множество периодов . Например, периодом функции у = < х > можно считать любое из чисел: 1, 2, 3, –1, – 2, – 3 и т. д.
Говоря о периоде функции у = f ( x ), обычно имеют в виду наименьший положительный период. Так, мы говорим, периодом функции < х > является число 1.
Покажем, что 2 π – период функции y = cos x .
Так функция y = cos x определена на всей числовой оси, то достаточно показать, что f ( x +2 π )= f ( x ). с os ( x +2 π )= cos x по формулам приведения, т.е. 2 π – период функции.
Покажем теперь, что 2 π – наименьший положительный период.
Пусть Т >0 – период косинуса, т.е. для любого х выполняется равенство cos ( x + Т) = cosx . Положим х =0, получим сos Т =1. Отсюда Т =2 π k , kZ . Так как Т >0, то Т может принимать значения 2 π , 4 π , 6 π , …, и поэтому период не может быть меньше 2 π .
Доказать дома самостоятельно, что наименьший положительный период функции y = sin x равен 2 π .
Покажем, что функция y = tg x является периодической с периодом π .
Если х принадлежит области определения этой функции, т.е. х ≠ p /2+ p n , n Î Z , то по формулам приведения получаем tg ( x - π )= - tg ( π- x )= - (- tgx )= tg x , tg ( x + π )= t g x .
Таким образом, tg ( x -π )= tg x = tg ( x +π ). Следовательно, π – период функции у= tgx .
Покажем, что π – наименьший положительный период функции у= tg x .
Пусть Т период тангенса, тогда tg ( x +Т )= tg x , откуда при х =0 получаем tg Т =0, T = kπ , k Z . Так как наименьшее целое положительное k равно 1, то π – наименьший положительный период функции у= tg x .
Доказать дома самостоятельно, что наименьший положительный период функции y = ctg x равен π .

В данном видеоуроке мы вспомним формулы, позволяющие перейти от вычисления синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов, а также формулы приведения. Поговорим о чётности, нечётности тригонометрических функций, а также об их периодичности.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Чётность, нечётность, периодичность тригонометрических функций"
Сегодня на уроке мы с вами вспомним формулы, позволяющие перейти от вычисления синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов, а также формулы приведения. Напомним, какие функции называются тригонометрическими. Поговорим о чётности, нечётности тригонометрических функций, а также об их периодичности.
Прежде чем приступить к рассмотрению новой темы, давайте вспомним формулы, которые позволяют сводить вычисление значений синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов.
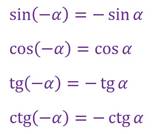
, ,
, ,
, ,
, .
Вспомним формулы приведения для синуса, косинуса, тангенса и котангенса.
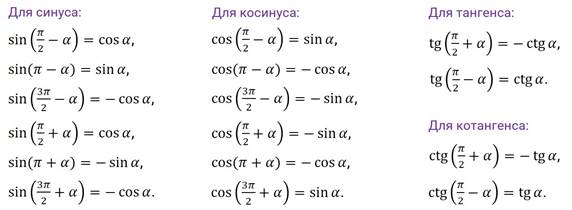
На прошлом занятии мы с вами сказали, что функции , , и называются тригонометрическими функциями.
Также на прошлом занятии мы выяснили, что функция определена на множестве действительных чисел. Для любого значения верно равенство . Следовательно, функция – нечётная функция.
Функция определена на множестве действительных чисел. Для любого значения верно равенство . Следовательно, функция и – чётная функция.
Областью определения функции является множество действительных чисел, кроме , . Для любого из области определения верно равенство . Следовательно, функция – нечётная функция.
Областью определения функции является множество действительных чисел, кроме , . Для любого из области определения верно равенство . Следовательно, функция – нечётная функция.
Отметим, что при исследовании функции на чётность или нечётность мы будем находить её область определения, чтобы убедиться, что эта область определения симметрична относительно начала координат.
Давайте выполним задание. Установите чётность или нечётность функций:
а) ; б) .
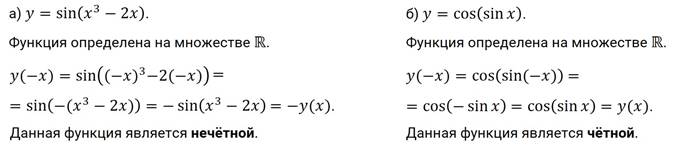
Мы знаем, что для любого значения верны равенства: , . Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на . Такие функции называются периодическими с периодом .
Функция называется периодической, если существует такое число , что для любого из области определения этой функции выполняется равенство

.
Число называется периодом функции .
Из этого определения следует, что если принадлежит области определения функции , то числа , и все числа , где , также принадлежат области определения этой периодической функции и , где .
Число является наименьшим положительным периодом для функций и .

Давайте докажем это, например, для функции .
Пусть – период косинуса, то есть равенство выполняется для любого . При получаем , . Отсюда , .
Так как , то может принимать значения при , при , при и так далее.
Поэтому период не может быть меньше . То есть – наименьший положительный период функции .
Задание. Докажите, что – периодическая функция с периодом .
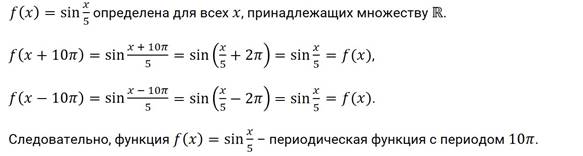
Теперь докажем, что функция является периодической с наименьшим положительным периодом .
Итак, пусть принадлежит области определения функции , то есть множеству действительных чисел, кроме , .
, .
Таким образом, мы получили, что . Следовательно, – период функции .
Докажем, что это наименьший положительный период функции . Пусть – период тангенса, тогда .
При получаем , . Откуда , .
При , то есть при наименьшем целом положительном, получаем . Следовательно, – наименьший положительный период функции .
Отметим, что функция также является периодической с наименьшим положительным периодом .
Задание. Докажите, что – периодическая функция с периодом .

Задание. Докажите, что – периодическая функция с периодом .

Отметим, что периодическими функциями описываются такие физические процессы, как колебания маятника, вращение планет, переменный ток и так далее.
Сейчас на рисунке вы видите графики некоторых периодических функций. Отметим, что график периодической функции имеет один и тот же вид на всех последовательных отрезках числовой прямой, длина которых равна периоду.

Следовательно, значения Sin и Cos периодически повторяются при изменении аргумента на 2 π .
Такие функции называются периодическими с периодом 2 π .

Функция f(x) называется периодической , если существует такое число T ≠ 0 , что для любого x из области определения этой функции выполняется равенство
Число T называется периодом функции f(x).
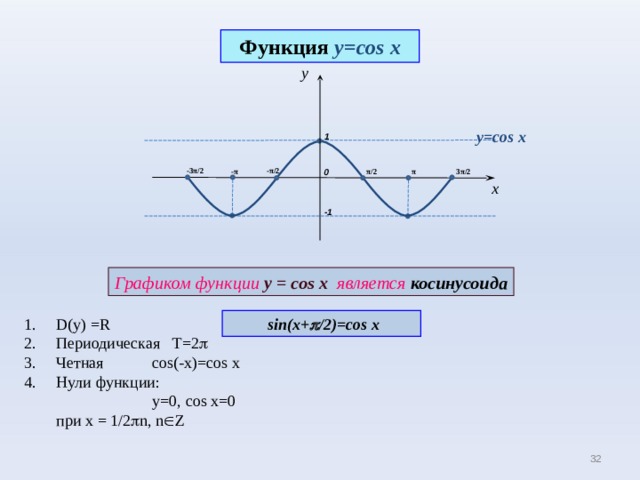
Функция y = cos x
y=cos x
-3 π /2
- π /2
3 π /2
Графиком функции у = cos x является косинусоида
- D(y) =R
- Периодическая Т=2
- Четная cos(-x)=cos x
- Нули функции:
у=0, cos x=0 при х = 1/2 n, n Z
sin(x+ /2)=cos x

ПОКАЖЕМ, ЧТО ЧИСЛО 2 Π ЯВЛЯЕТСЯ НАИМЕНЬШИМ ПОЛОЖИТЕЛЬНЫМ ПЕРИОДОМ ФУНКЦИИ Y = COS X.
Пусть Т › 0 – период косинуса, т.е. для любого x выполняется равенство
Cos (x + T) = Cos x. Положив x = 0 , получим Cos T = 1. Отсюда T = 2 π k, k є Ζ . Так как Т › 0, то Т может принимать значения 2 π , 4 π , 6 π , …, и поэтому период не может быть меньше 2 π .
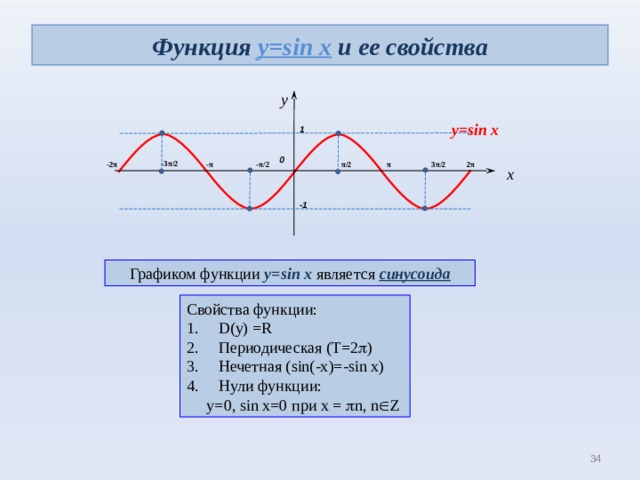
Функция y=sin x и ее свойства
y=sin x
-3 π /2
3 π /2
- 2 π
- π /2
Графиком функции y=sin x является синусоида
- D(y) =R
- Периодическая (Т=2 )
- Нечетная ( sin(-x)=-sin x)
- Нули функции:
у=0, sin x=0 при х = n, n Z

АНАЛОГИЧНО МОЖНО ДОКАЗАТЬ, ЧТО НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = SIN X ТАКЖЕ РАВЕН 2 Π
Доказать, что f(x) = Sin 3x – периодическая функция с периодом ( 2 π ) /3.
Доказательство :
Данная функция определена для всех x є R , поэтому достаточно показать, что для любого x верно равенство f(x + T) = f(x) .
= Sin (3x + 2 π ) = Sin 3x = f(x)
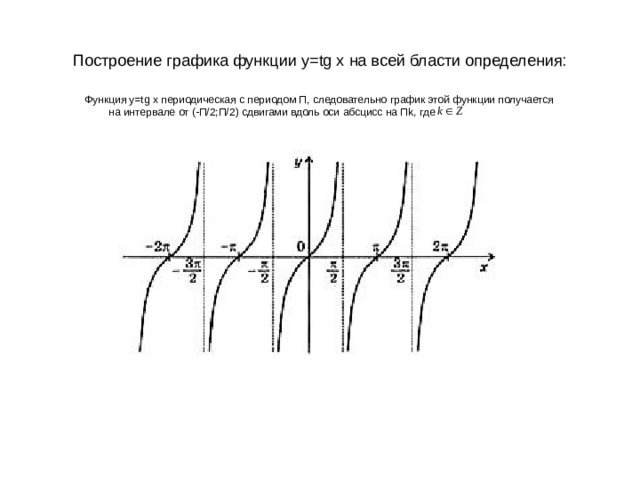
Построение графика функции у= tg x на всей бласти определения:
Функция у= tg x периодическая с периодом П, следовательно график этой функции получается на интервале от (-П/2;П/2) сдвигами вдоль оси абсцисс на П k, где
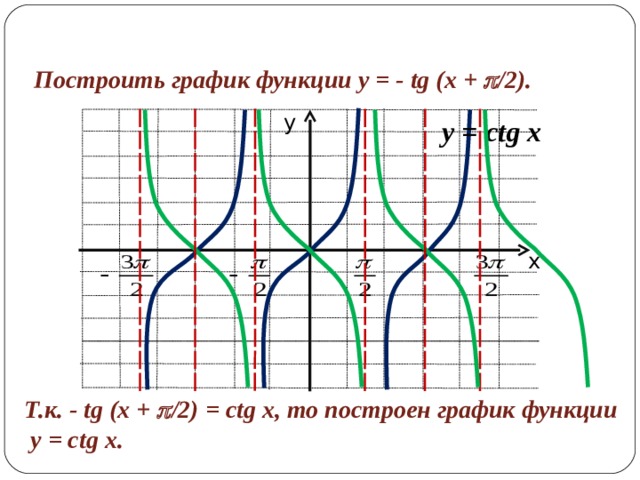
Построить график функции y = - tg (x + /2) .
y = ctg x
Т.к. - tg (x + /2) = ctg x , то построен график функции
y = ctg x .

ПОКАЖЕМ, ЧТО ФУНКЦИЯ Y= TG X ЯВЛЯЕТСЯ ПЕРИОДИЧЕСКОЙ С ПЕРИОДОМ Π .
Если x принадлежит области определения этой функции, т.е. x ≠ - π /2 + π n, n є Ζ , то по формулам приведения получаем
tg(x – π ) = -tg( π – x) = -(-tg x) = tg x
Таким обтазом, tg(x – π ) = tg x = tg(x + π ). Следовательно, π – период функции у = tg x.

ПОКАЖЕМ, ЧТО Π – НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = TG X.
Пусть Т – период тангенса, тогда tg(x + T) = tg x, откуда при x = 0 получаем tg T = 0, T = k π , k є Ζ . Так как наименьшее целое положительное k равно 1, то π – наименьший положительный период функции y = tg x.

ДОКАЗАТЬ, ЧТО У = TG (X/3) – ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ С ПЕРИОДОМ 3 Π .
Доказательство :
Так как tg ((x + 3 π )/3) = tg (x/3 + π ) = tg (x/3)
tg((x - 3 π )/3) = tg(x/3 – π ) = tg (x/3), то tg(x/3) – периодическая функция с периодом 3 π .
Читайте также:

