Конспект связь между координатами векторов и координатами точек

Обновлено: 30.06.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Поурочный план учителя Мосейчука В.В.

Предмет: Геометрия

Определить формулу, связывающую координаты вектора с координатами точек.

Задачи урока

Ввести понятие радиус-вектора произвольной точки пространства.

Найти формулу нахождения координат вектора по координатам его начала и конца.

Ввести формулы координат середины отрезка, модуля вектора, расстояния между двумя точками.

Отработать навыки применения данных формул в стандартных ситуациях.

Развить умения точно излагать свои мысли.

Планируемые результаты

Обучающийся должен знать формулу связи координат вектора и координат его начала и конца, формулы координат середины отрезка, модуля вектора, расстояния между двумя точками. Обучающийся должен уметь находить координаты вектора, координаты середины отрезка, модуль вектора, расстояние между двумя точками

Техническое обеспечение урока

Дополнительные методическое и дидактическое обеспечение урока

Содержание урока

Организационный момент (1 мин);

Постановка проблемной задачи (1 мин);

Изучение нового материала (10 мин);

Закрепление изученного материала (10 мин);

Применение знаний и умений в стандартной ситуации (20 мин)

Постановка домашнего задания (1 мин);

Подведение итогов урока (2 мин).

Деятельность учителя

Деятельность обучающихся

ОРГАНИЗАЦИОННЫЙ МОМЕНТ

Приветствует обучающихся. Проверяет готовность к уроку.

ПОСТАНОВКА ПРОБЛЕМНОЙ ЗАДАЧИ

Какое основное понятие изучали на прошлом уроке?

Координаты каких математических объектов вы знаете?

Что такое вектор?

Возникает вопрос: можно ли установить связь между координатами начала и конца вектора и координатами самого вектора?

Следовательно, тема нашего урока какова?

Координаты в пространстве.

Координаты точки, координаты вектора.

Связь между координатами вектора и координатами точек.

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Пусть М (х, у, z ). Тогда

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

Устно по учебнику № 416, 417, 418.

Далее работа в парах № 419, 420.

Ведут комментированную работу с места.

Работают в парах, осуществляют взаимоконтроль.

ПРИМЕНЕНИЕ ЗНАНИЙ, УМЕНИЙ В СТАНДАРТНОЙ СИТУАЦИИ

При работе с учебником по пункту 45 заполните таблицу.

Название задачи

Формула решения

Координаты середины отрезка

Модуль вектора

Расстояние между двумя точками

Для закрепления формулы модуля вектора выполнить № 426 устно.

У доски решить № 424(а), № 429

Один ученик работает у доски, остальные в тетрадях.

Далее переходим к индивидуально-дифференцированной работе по карточкам.

Работают самостоятельно. Сдают на проверку.

ПОСТАНОВКА ДОМАШНЕГО ЗАДАНИЯ

№ 424(б), № 425 (б, в), № 427

Записывают домашнее задание

ПОДВЕДЕНИЕ ИТОГОВ УРОКА

Обобщить пройденный материал на уроке:

Мои знания углубились, потому что …………….

Мои умения изменились, так как ………………………….

В ходе работы на уроке я приобрел …………………….

Я хотел бы повторить ……….

Ведут диалог с учителем.

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 933 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 683 человека из 75 регионов

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

Курс добавлен 31.01.2022
Сейчас обучается 24 человека из 17 регионов

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 610 244 материала в базе

Материал подходит для УМК

1.3. Связь между координатами векторов и координатами точек

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

01.02.2018 5207
DOCX 129 кбайт
423 скачивания
Рейтинг: 4 из 5
Оцените материал:

Настоящий материал опубликован пользователем Мосейчук Виталий Васильевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Академическая стипендия для вузов в 2023 году вырастет до 1 825 рублей

Время чтения: 1 минута

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

Время чтения: 1 минута

Время чтения: 2 минуты

Рособрнадзор предложил дать возможность детям из ДНР и ЛНР поступать в вузы без сдачи ЕГЭ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Связь между координатами векторов и координатами точек"

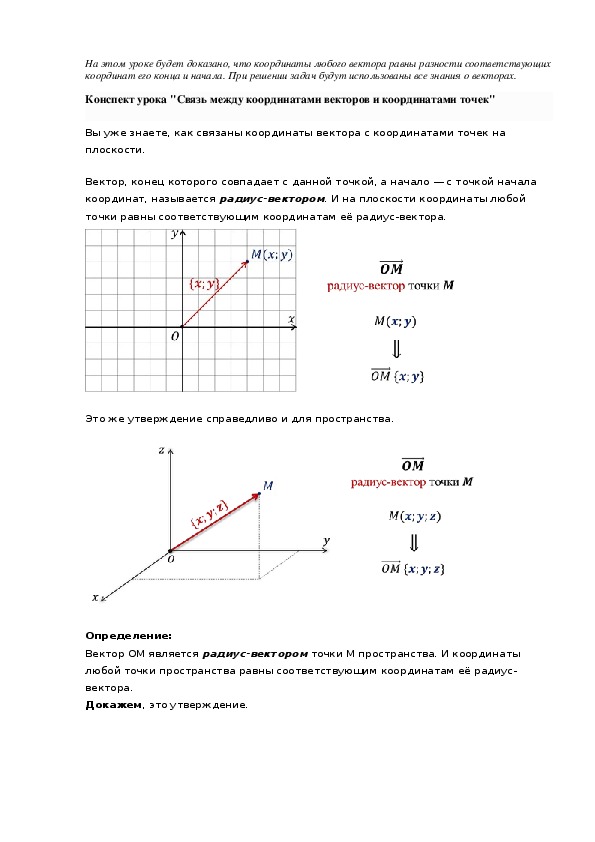
Вы уже знаете, как связаны координаты вектора с координатами точек на плоскости.

Вектор, конец которого совпадает с данной точкой, а начало — с точкой начала координат, называется радиус-вектором. И на плоскости координаты любой точки равны соответствующим координатам её радиус-вектора.

Это же утверждение справедливо и для пространства.

Определение:

Вектор ОМ является радиус-вектором точки М пространства. И координаты любой точки пространства равны соответствующим координатам её радиус-вектора.

Докажем, это утверждение.

Так, мы доказали, что координаты любой точки пространства равны соответствующим координатам её радиус-вектора.

Теперь выразим координаты произвольного вектора пространства АВ через координаты его начала и конца.

Пусть координаты начала А равны х₁, у₁ и z₁. А координаты конца B равны x₂, y₂ и z₂. Проведём радиус-векторы точек А и B. Понятно, что координаты вектора ОА равны соответствующим координатам точки А. А координаты вектора ОB равны координатам точки B.

Пользуясь правилом построения вектора разности двух векторов, можем отметить, что вектор АB равен разности векторов ОB и ОА. Почему ОB минус ОА, а не наоборот? Потому, что вектор разности направлен из конца вектора вычитаемого к концу вектора уменьшаемого. Значит, вектор ОB является уменьшаемым, а вектор ОА — вычитаемым.

Координаты векторов ОА и ОB известны. Тогда найдём координаты вектора АВ, как разности соответствующих координат векторов ОВ и ОА. Получаем, 2−𝑥₁; 𝑦₂−𝑦₁; 𝑧₂−𝑧₁>. Так мы выразили координаты вектора через координаты его начала и конца.

Можно сделать вывод, что каждая координата вектора равна разности соответствующих координат его конца и начала.

Задание: по координатам точек 𝐴(2;−3;0), 𝐵(7;−12;18) и 𝐶(−8;0;5) определить координаты векторов 𝑂𝐴, 𝑂𝐵, 𝑂𝐶, 𝐴𝐵, 𝐵𝐶 и 𝐴𝐶, если точка 𝑂 — точка начала координат.

Решение:

Задание: По координатам векторов 𝑂𝐴, 𝑂𝐵, 𝑂𝐶, 𝐴𝐷, 𝐵𝐸 и 𝐶𝐹 определить координаты точек 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 и 𝐹, если точка 𝑂 — точка начала координат.

Решение:

Мы рассмотрели примеры применения связи координат вектора и координат его начала и конца.

А сейчас поговорим о коллинеарных векторах.

Вы помните, если векторы А и В коллинеарны, то один можно выразить через другой умножением на некоторое число k. Причём, если , то векторы А и B сонаправлены, если же , то векторы А и B противоположно направлены.

Если координаты вектора , то координаты вектора .

Запишем отношения соответствующих координат данных векторов.

Все они равны между собой и равны k.

Так можно отметить, что если координаты векторов пропорциональны, то данные векторы коллинеарны.

Задание: по координатам векторов определить коллинеарны ли пары векторов.

Решение:

Задание: найти значения переменных m и n, при которых данные векторы будут коллинеарны.

Решение:

Вам также уже хорошо известно понятие компланарных векторов. Возникает вопрос, возможно, ли по координатам векторов определить компланарны они или нет?

Напомним, что компланарными называют векторы, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Другими словами, векторы компланарны, если имеются равные им векторы, лежащие в одной плоскости.

Так же мы выяснили, что любые два вектора всегда компланарны, а вот три вектора могут быть как компланарными, так и не компланарными.

В связи с этим мы доказали признак компланарности векторов.

Если вектор можно разложить по векторам и : , то векторы , и компланарны.

Справедливо также и обратное утверждение, которое называют свойством компланарных векторов.

Если векторы , и компланарны (), то вектор можно разложить по векторам и : , причём коэффициенты разложения определяются единственным образом.

Задание: рассмотрим тройки векторов с известными координатами и выясним компланарны они или нет.

Решение:

Вы узнали, что радиус-вектором точки в пространстве называется вектор, конец которого совпадает с данной точкой, а начало — с точкой начала координат. Координаты любой точки равны соответствующим координатам её радиус-вектора.

Мы с вами доказали, что каждая координата вектора равна разности соответствующих координат его конца и начала. А также, пользуясь тем, что любой вектор можно выразить через коллинеарный ему вектор, мы отметили, что если координаты векторов пропорциональны, то данные векторы коллинеарны. Также мы рассмотрели примеры определения компланарности векторов по их координатам.

Теорема. Координаты любой точки равны координатам её радиус-вектора.

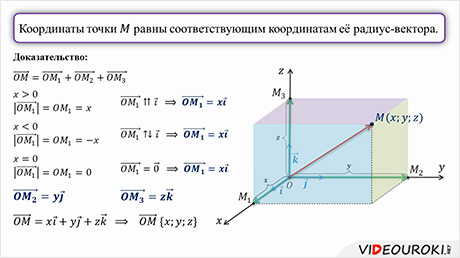
Пусть точка М имеет координаты ( x; y; z ). Пусть М₁ , М₂ , М₃ – точки пересечения с осями координат плоскостей, проходящих через точку М перпендикулярно к этим осям. Тогда

Если точка М₁ лежит на положительной полуоси абсцисс, как на рисунке, то х = OМ₁ , а векторы и сонаправлены. Поэтому . Если точка М₁ лежит на отрицательной полуоси абсцисс, то х = –OМ₁ , а векторы и противоположно направлены. Поэтому . Таким образом, в любом случае .

Аналогично доказывается, что

Подставив эти выражения в равенство, получим

Отсюда следует, что координаты вектора равны ( x; y; z ), т.е. координаты точки М равны соответствующим координатам её радиус-вектора . Теорема доказана.

Пользуясь данным утверждением, выразим координаты вектора через координаты его начала А и конца В . Пусть точка А имеет координаты ( x₁; y₁; z₁ ), а точка В – координаты ( x₂; y₂; z₂ ). Вектор равен разности векторов и , поэтому его координаты равны разностям соответствующих координат векторов и . Но координаты векторов и совпадают с соответствующими координатами точек В и А :

( x₂; y₂; z₂ ),

( x₁; y₁; z₁ ).

Поэтому вектор имеет координаты < x₂–x₁, y₂–y₁, z₂–z₁ >.

Итак, каждая координата вектора равна разности соответствующих координат его конца и начала .

Есть две произвольные точки A₁(x₁;y₁;z₁) и A₂(x₂;y₂;z₂). Тогда серединой отрезка A₁A₂ будет точка С с координатами x, y, z, где

Бесплатное участие. Свидетельство СМИ сразу.
До 500 000 руб. ежемесячно и 10 документов.

На этом уроке будет доказано, что координаты любого вектора равны разности соответствующих координат его конца и начала. При решении задач будут использованы все знания о векторах.Вы уже знаете, как связаны координаты вектора с координатами точек на плоскости. Вектор, конец которого совпадает с данной точкой, а начало — с точкой начала координат, называется радиус-вектором. И на плоскости координаты любой точки равны соответствующим координатам её радиус-вектора

Связь между координатами векторов и координатами точек.docx

На этом уроке будет доказано, что координаты любого вектора равны разности соответствующих координат его конца и начала. При решении задач будут использованы все знания о векторах. Конспект урока "Связь между координатами векторов и координатами точек" Вы уже знаете, как связаны координаты вектора с координатами точек на плоскости. Вектор, конец которого совпадает с данной точкой, а начало — с точкой начала координат, называется радиус-вектором. И на плоскости координаты любой точки равны соответствующим координатам её радиус-вектора. Это же утверждение справедливо и для пространства. Определение: Вектор ОМ является радиус-вектором точки М пространства. И координаты любой точки пространства равны соответствующим координатам её радиус- вектора. Докажем, это утверждение. Так, мы доказали, что координаты любой точки пространства равны соответствующим координатам её радиус-вектора. Теперь выразим координаты произвольного вектора пространства АВ через координаты его начала и конца. Пусть координаты начала А равны х1, у1 и z1. А координаты конца B равны x2, y2 и z2. Проведём радиус-векторы точек А и B. Понятно, что координаты вектора ОА равны соответствующим координатам точки А. А координаты вектора ОB равны координатам точки B. Пользуясь правилом построения вектора разности двух векторов, можем отметить, что вектор АB равен разности векторов ОB и ОА. Почему ОB минус ОА, а не наоборот? Потому, что вектор разности направлен из конца вектора вычитаемого к концу вектора уменьшаемого. Значит, вектор ОB является уменьшаемым, а вектор ОА — вычитаемым. Координаты векторов ОА и ОB известны. Тогда найдём координаты вектора АВ, как разности соответствующих координат векторов ОВ и ОА. Получаем, <2−1; 2−1; 2−1>. Так мы выразили координаты вектора через координаты его начала и конца. Можно сделать вывод, что каждая координата вектора равна разности соответствующих координат его конца и начала. Задание: по координатам точек (2;−3;0), (7;−12;18) и (−8;0;5) определить координаты векторов , , , , и , если точка — точка начала координат. Решение: Задание: По координатам векторов , , , , и определить координаты точек , , , , и , если точка — точка начала координат. Решение: Мы рассмотрели примеры применения связи координат вектора и координат его начала и конца. А сейчас поговорим о коллинеарных векторах. Вы помните, если векторы А и В коллинеарны, то один можно выразить через другой умножением на некоторое число k. Причём, если , то векторы А и B сонаправлены, если же направлены. , то векторы А и B противоположно Если координаты вектора , то координаты вектора . Запишем отношения соответствующих координат данных векторов. Все они равны между собой и равны k. Так можно отметить, что если координаты векторов пропорциональны, то данные векторы коллинеарны. Задание: по координатам векторов определить коллинеарны ли пары векторов. Решение: Задание: найти значения переменных m и n, при которых данные векторы будут коллинеарны. Решение: Вам также уже хорошо известно понятие компланарных векторов. Возникает вопрос, возможно, ли по координатам векторов определить компланарны они или нет? Напомним, что компланарными называют векторы, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Другими словами, векторы компланарны, если имеются равные им векторы, лежащие в одной плоскости. Так же мы выяснили, что любые два вектора всегда компланарны, а вот три вектора могут быть как компланарными, так и не компланарными. В связи с этим мы доказали признак компланарности векторов. Если вектор и компланарны. Справедливо также и обратное утверждение, которое называют свойством компланарных векторов. Если векторы векторам и единственным образом. Задание: рассмотрим тройки векторов с известными координатами и выясним компланарны они или нет. Решение: , причём коэффициенты разложения определяются можно разложить по векторам ), то вектор можно разложить по и компланарны ( и : , то векторы , , : Итоги: Вы узнали, что радиус-вектором точки в пространстве называется вектор, конец которого совпадает с данной точкой, а начало — с точкой начала координат. Координаты любой точки равны соответствующим координатам её радиус- вектора. Мы с вами доказали, что каждая координата вектора равна разности соответствующих координат его конца и начала. А также, пользуясь тем, что любой вектор можно выразить через коллинеарный ему вектор, мы отметили, что если координаты векторов пропорциональны, то данные векторы коллинеарны. Также мы рассмотрели примеры определения компланарности векторов по их координатам.

Читайте также: