Изображение пространственных фигур конспект
Обновлено: 03.07.2024
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Дисциплина: Математика.
Преподаватель: Домашкина А.С.
ПЛАН ЗАНЯТИЯ
Тема программы 3: Геометрия. Параллельность прямых и плоскостей.
Тема занятия 17-18 : Изображение пространственных фигур на плоскости.
Повторить свойства параллельных прямых и плоскостей.
Свойства параллельного проецирования.
Научиться правильно изображать плоские фигуры и объёмные тела на плоскости.
Формирование грамотной математической речи, умения слушать, анализировать, строить логические цепочки, делать выводы, работать с чертежами.
Формирование трудовых навыков, умения распределять своё рабочее время на занятии, быстро, грамотно и аккуратно оформлять записи в своих конспектах.
Формирование математического мировоззрения, математической культуры, культуры речи, использование математических терминов и символики.
Формирование умения чётко и ясно излагать свои мысли, обсуждать и корректировать высказывания своих одногруппников.
Формирование интереса к предмету математики путём использования формы занятия беседа-лекция-практикум, использования наглядности (моделей).
Тип занятия : изучение нового материала.
Дидактическое обеспечение:
Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Презентация к занятию.
Инструменты и оборудование: мел, доска, линейка.
Литература: Мордкович, А.Г. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч.1. Учебник. – М.: Мнемозина, 2010.
Формирование компетенций в соответствии с ФГОС:
ОК:
Социальная компетентность – способность действовать в социуме с учётом позиций других людей.
Коммуникативная компетентность – способность вступать в коммуникацию с целью быть понятым.
Предметная компетентность – способность анализировать и действовать с позиции отдельных областей человеческой культуры.
Математическая компетентность – умение работать с числом, числовой информацией.
Ход занятия
1. Организационный момент:
в) отметить отсутствующих;
Критерии оценивания:
наличие лекции + верное решение всех заданий - ”5” ;
наличие лекции + решение всех заданий, но есть недочеты - “4”;
наличие лекции + решение всех заданий с недочетами и ошибками - ”3”.
Актуализация знаний (повторение изученного материала/внеаудиторной самостоятельной работы):
Чтобы работа на уроке была плодотворной, давайте вспомним некоторые факты, характеризующие свойства параллельных прямых и плоскостей. Ваша задача определить верность следующих высказываний:
Верно ли, что через любую точку пространства можно провести множество прямых параллельных данной прямой?
По теореме о существовании прямой, параллельной данной прямой через точку пространства можно провести единственную прямую.
Верно ли, что если одна из двух параллельных прямых пересекает плоскость, то и другая тоже пересекает эту плоскость?
По лемме о пересечении плоскости двумя параллельными прямыми, если одна из параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Верно ли, что две непересекающиеся прямые в пространстве параллельны?
В пространстве не имеют общих точек параллельные и скрещивающиеся прямые.
Верно ли, что если две прямые параллельны некоторой плоскости, то они параллельны друг другу?
Эти прямые могут быть не только параллельными, но и пересекаться, а также они могут быть скрещивающимися.
Объяснение нового материала:
Для решения этой задачи применяется метод параллельного проектирования . Выясним его суть на примере простейшей геометрической фигуры – точки.
Итак, у нас есть геометрическая фигура в пространстве – точка А. (слайд 2)
Выберем в пространстве произвольную плоскость (её мы будем называть плоскостью проекций ) и любую прямую a пересекает (она задает направление параллельного проектирования). (слайд 3)
Проведем через точку А прямую, параллельную прямой а . Точка А’ пересечения этой прямой с плоскостью и есть проекция точки А на плоскость . Точку А ещё называют прообразом , а точку А’ – образом . Если А , то А’ совпадает с А. (слайд 4)
Наглядным примером параллельного проектирования является отбрасываемая любым объектом( прообраз ) в пространстве тень( образ ) от солнечных лучей( направление параллельного проектирования ) на Земле( плоскость проекций ). (слайд 5)
Примечание 1. При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции (самостоятельно обоснуйте почему). (слайд 6)
Примечание 2. При параллельном проектировании плоских фигур не выбирают направление параллельного проектирования параллельно плоскости, которой принадлежит эта плоская фигура, т.к. получающаяся при этом проекция не отражает свойства данной плоской фигуры. (слайд 7)
Примечание 3. Если направление параллельного проектирования перпендикулярно плоскости проекций, то такое параллельное проектирование называется ортогональным (прямоугольным) проектированием . (слайд 8)
Примечание 4. Если плоскость проекций и плоскость, в которой лежит данная фигура параллельны ( ||(АВС)), то получающееся при этом изображение… правильно – равно прообразу! (слайд 9)
Параллельное проектирование обладает свойствами:
параллельность прямых (отрезков, лучей) сохраняется ; (слайд 10)
отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется ; (слайд 11)
Если, например, АВ=2 CD , то А’В’=2 C ’ D ’ или
3) Линейные размеры плоских фигур(длины отрезков, величины углов) не сохраняются (исключение – см. примечание 4). (слайд 12)
5. Закрепление материала:
Построим изображение куба: (слайд 13)
Далее разберем примеры изображения некоторых плоских фигур: (слайд 14)
Разберемся, как построить изображение правильного шестиугольника.
Разобьем правильный шестиугольник на три части: прямоугольник FBCE и два равнобедренных треугольника Δ FAB и Δ CDE . Построим вначале изображение прямоугольника FBCE – произвольный параллелограмм FBCE . Осталось найти местоположение двух оставшихся вершин – точек A и D .
Вспомнив свойства правильного шестиугольника, заметим, что: 1) эти вершины лежат на прямой, проходящей через центр прямоугольника и параллельной сторонам BC и FE ; 2) OK = KD и ON = NA .
Находим на изображении точку О и проводим через неё прямую, параллельную BC и FE , получив при этом точки N и K .
Откладываем от точек N и K от центра О на прямой такие же отрезки – в итоге получаем две оставшиеся вершины правильного шестиугольника A и D . (слайд 18)
6. Подведение итогов занятия:
1. Что является параллельной проекцией отрезка, треугольника, прямоугольника, квадрата, окружности?
2. Какие величины не изменяются при параллельном проецировании? (длина отрезка, градусная мера углов, отношения длин отрезков, отношение площадей двух фигур)?
3. Может ли при параллельном проецировании параллелограмма получиться трапеция и наоборот?
7. Рефлексия:
Предлагаю обучающимся закончить предложения на выбор:
• сегодня я узнал…
8. Домашнее задание:
Попробуйте самостоятельно построить изображение правильного пятиугольника .
Подсказка : разбейте фигуру на две части – равнобокую трапецию и равнобедренный треугольник, а затем воспользуйтесь некоторыми свойствами этих фигур и, конечно же, свойствами параллельного проектирования.

В этом видеоуроке мы напомним, что называют параллельным проектированием. Вспомним основные его свойства. Повторим, как свойства параллельного проектирования применяются при выполнении рисунков, иллюстрирующих теоремы и задачи стереометрии.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Параллельное проектирование. Изображение пространственных фигур"
В стереометрии большое значение имеет умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости пространственные фигуры.
Итак, зачастую для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование. Определяется оно следующим образом.
Пусть — некоторая плоскость, а — некоторая прямая, пересекающая эту плоскость. Возьмём в пространстве произвольную точку . Если точка не лежит на прямой , то проведём через точку прямую, параллельную прямой , и обозначим через точку пересечения этой прямой с плоскостью . Если же точка лежит на прямой , то обозначим через точку пересечения прямой с плоскостью .

Точка называется проекцией точки на плоскость при проектировании параллельно прямой (или параллельной проекцией точки ).
Плоскость называется плоскостью проекций, а о прямой говорят, что она задаёт направление проектирования.

Все прямые, параллельные прямой , задают одно и то же направление проектирования, поэтому также называются проектирующими прямыми.
Пусть — плоская или пространственная фигура. Проекцией фигуры на плоскость при проектировании параллельно прямой называется множество проекций всех точек фигуры.
Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.

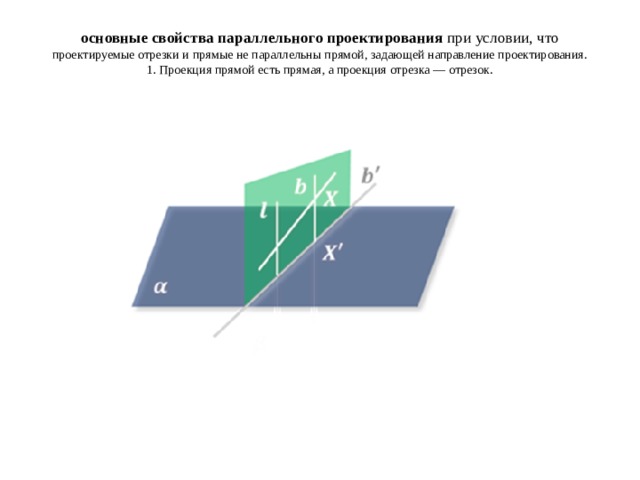
Вспомним основные свойства параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования.
1. Проекция прямой есть прямая, а проекция отрезка — отрезок.

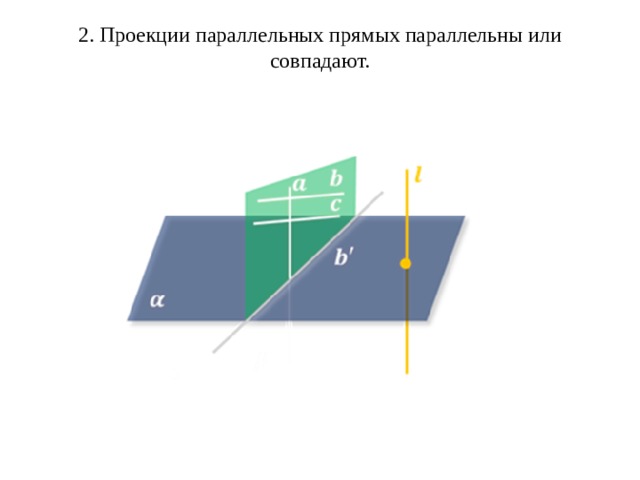
2. Проекции параллельных прямых параллельны или совпадают.

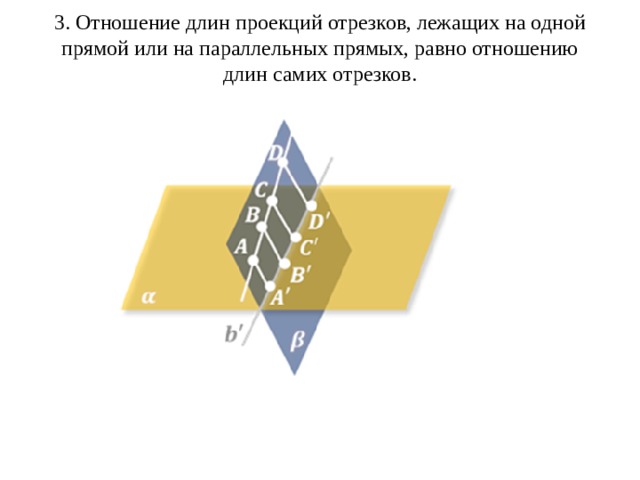
3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.

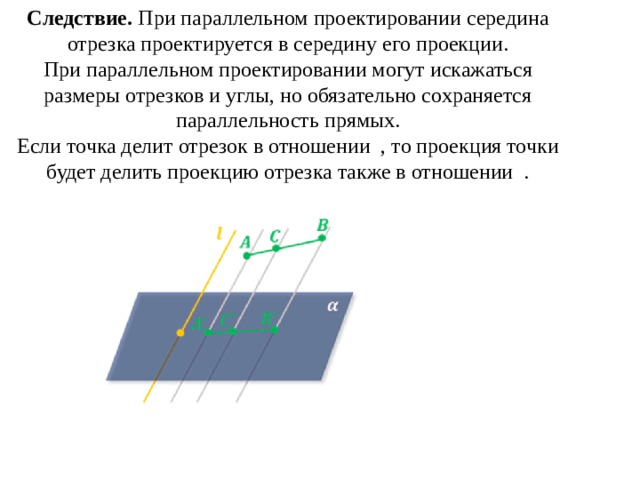
Следствие. При параллельном проектировании середина отрезка проектируется в середину его проекции.
При параллельном проектировании могут искажаться размеры отрезков и углы, но обязательно сохраняется параллельность прямых.
Если точка делит отрезок в отношении , то проекция точки будет делить проекцию отрезка также в отношении .

Центр правильного треугольника отображается в точку пересечения медиан проекции этого треугольника, центр квадрата — в точку пересечения диагоналей проекции квадрата.

А теперь давайте поговорим об изображении пространственных фигур.
Рассмотренные свойства параллельного проектирования применяются при выполнении рисунков (изображений фигур), иллюстрирующих теоремы и задачи стереометрии.

Изображением фигуры называется любая фигура, подобная проекции этой фигуры на некоторую плоскость.

Выполняя изображения фигур, расположенных в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном проектировании, а в остальном изображение может быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были наглядными и давали верное представление о них.
При различном выборе плоскости проекций и направления проектирования получаются различные проекции данной фигуры, а значит, и различные её изображения.
Например, вы видите фигуры, которые являются изображениями куба.

Причём изображение куба, данное на первом рисунке, не даёт представления о кубе, наглядным является изображение, которое дано на последнем рисунке.
При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования.
Итак, проекцией треугольника может быть любой треугольник.

При этом величины углов и отношение длин непараллельных сторон не сохраняются, но при этом медианы треугольника отображаются в медианы его проекции. В частности, за изображение прямоугольного, равнобедренного, равностороннего треугольников можно принять любой треугольник.
Параллелограмм проектируется в параллелограмм, так как параллельные прямые сохраняют параллельность.

В частном случае за изображение прямоугольника, квадрата, ромба можно принять любой параллелограмм.
Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований.

Правильный шестиугольник проектируется в искажённый шестиугольник с сохранением параллельности противолежащих сторон.

Окружность проектируется в эллипс, большая ось которого имеет длину, равную диаметру окружности.

При изображении пространственных фигур пользуются тем фактом, что фигуру, состоящую из сторон и диагоналей любого выпуклого или невыпуклого четырёхугольника, можно считать изображением треугольной пирамиды при определённом выборе направления проектирования и плоскости, на которую проектируется эта пирамида.

Например, фигуры, изображённые на экране, являются изображениями треугольной пирамиды при соответствующем выборе направления проектирования.

Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.

При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.

Аналогичным образом изображается прямоугольный параллелепипед.

Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий её основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.

Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить её с вершинами многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.

Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.

Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через неё две образующие, являющиеся касательными к этому эллипсу.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Точки и находятся по одну сторону от плоскости . Точки и — их параллельные проекции на эту плоскость, причём . Постройте точку пересечения прямой с плоскостью . И найдите расстояние между серединой отрезка и её проекцией на плоскость , если и см.



Задача вторая. На диагонали параллелепипеда взята точка , а на прямой – точка так, что отрезки и параллельны. Найти их отношение.
Рассмотрим вопрос об изображении пространственных фигур.
Рассмотренные свойства параллельного проектирования применяются при выполнении рисунков (изображений фигур), иллюстрирующих теоремы и задачи стереометрии.

Изображением фигуры называется любая фигура, подобная проекции этой фигуры на некоторую плоскость.

Выполняя изображения фигур, расположенных в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном проектировании, а в остальном изображение может быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были наглядными и давали верное представление о них.
При различном выборе плоскости проекций и направления проектирования получаются различные проекции данной фигуры, а значит, и различные её изображения.
Например, вы видите фигуры, которые являются изображениями куба.

Причём изображение куба, данное на первом рисунке, не даёт представления о кубе, наглядным является изображение, которое дано на последнем рисунке.
I.При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования. При этом:
Проекцией треугольника может быть любой треугольник

При этом величины углов и отношение длин непараллельных сторон не сохраняются, но при этом медианы треугольника отображаются в медианы его проекции. В частности, за изображение прямоугольного, равнобедренного, равностороннего треугольников можно принять любой треугольник.
Параллелограмм проектируется в параллелограмм, так как параллельные прямые сохраняют параллельность

В частном случае за изображение прямоугольника, квадрата, ромба можно принять любой параллелограмм.
Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований

Рассмотрим вопрос об изображении пространственных фигур.
Рассмотренные свойства параллельного проектирования применяются при выполнении рисунков (изображений фигур), иллюстрирующих теоремы и задачи стереометрии.

Изображением фигуры называется любая фигура, подобная проекции этой фигуры на некоторую плоскость.

Выполняя изображения фигур, расположенных в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном проектировании, а в остальном изображение может быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были наглядными и давали верное представление о них.
При различном выборе плоскости проекций и направления проектирования получаются различные проекции данной фигуры, а значит, и различные её изображения.
Например, вы видите фигуры, которые являются изображениями куба.

Причём изображение куба, данное на первом рисунке, не даёт представления о кубе, наглядным является изображение, которое дано на последнем рисунке.
I.При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования. При этом:
Проекцией треугольника может быть любой треугольник

При этом величины углов и отношение длин непараллельных сторон не сохраняются, но при этом медианы треугольника отображаются в медианы его проекции. В частности, за изображение прямоугольного, равнобедренного, равностороннего треугольников можно принять любой треугольник.
Параллелограмм проектируется в параллелограмм, так как параллельные прямые сохраняют параллельность

В частном случае за изображение прямоугольника, квадрата, ромба можно принять любой параллелограмм.
Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований

В стереометрии большое значение имеет умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости пространственные фигуры. Итак, зачастую для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование . Определяется оно следующим образом.

Пусть — некоторая плоскость, а — некоторая прямая, пересекающая эту плоскость. Возьмём в пространстве произвольную точку . Если точка не лежит на прямой , то проведём через точку прямую, параллельную прямой , и обозначим через точку пересечения этой прямой с плоскостью . Если же точка лежит на прямой , то обозначим через точку пересечения прямой с плоскостью .
Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.
основные свойства параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования. 1. Проекция прямой есть прямая, а проекция отрезка — отрезок.
2. Проекции параллельных прямых параллельны или совпадают.
3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
Следствие. При параллельном проектировании середина отрезка проектируется в середину его проекции. При параллельном проектировании могут искажаться размеры отрезков и углы, но обязательно сохраняется параллельность прямых. Если точка делит отрезок в отношении , то проекция точки будет делить проекцию отрезка также в отношении .
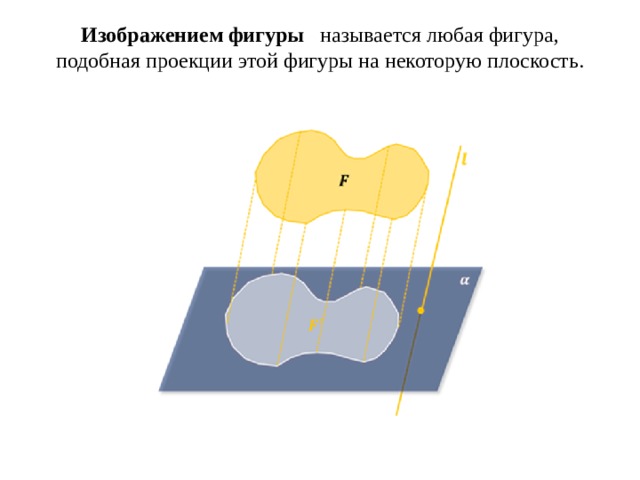
Изображением фигуры называется любая фигура, подобная проекции этой фигуры на некоторую плоскость.
Причём изображение куба, данное на первом рисунке, не даёт представления о кубе, наглядным является изображение, которое дано на последнем рисунке.
При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования.
Итак, проекцией треугольника может быть любой треугольник.
Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований .
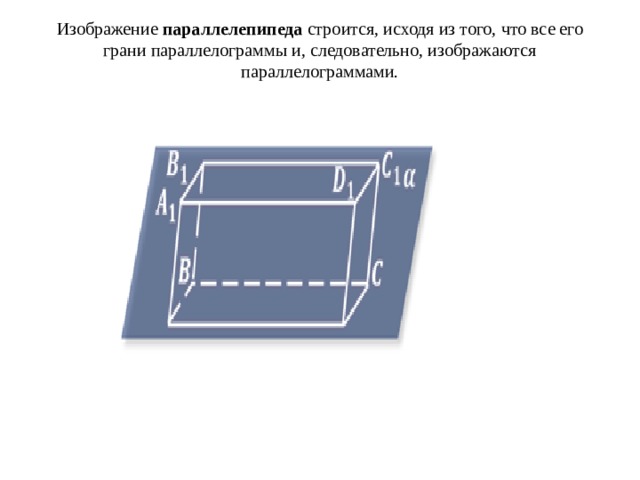
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.
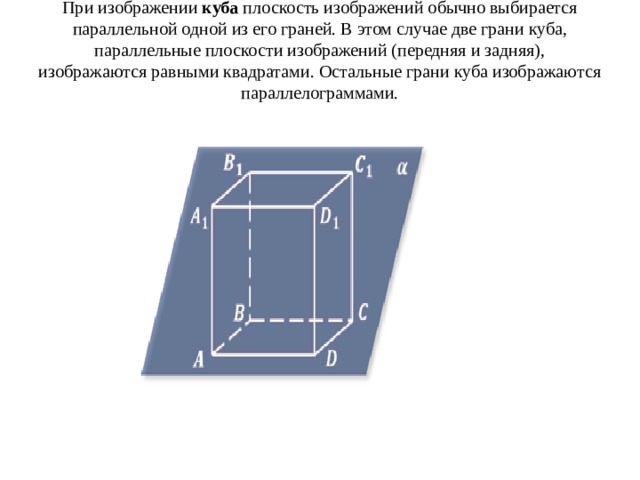
При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.
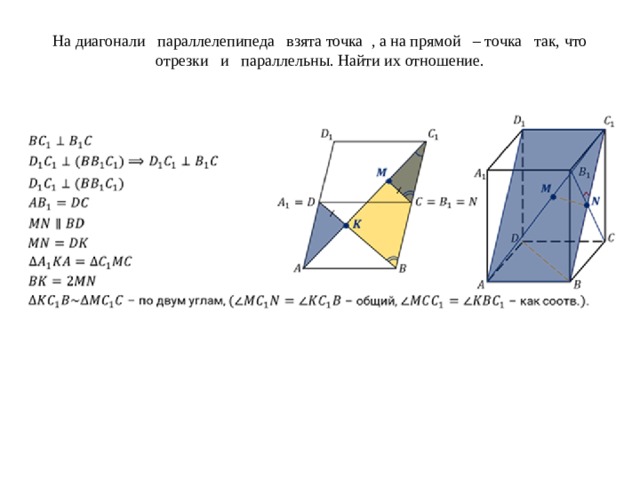
На диагонали параллелепипеда взята точка , а на прямой – точка так, что отрезки и параллельны. Найти их отношение.
Читайте также:

