Как найти наибольшее и наименьшее значение линейной функции кратко

Обновлено: 07.07.2024

Так как функция линейная, то будет возрастать (или убывать) на всем множестве определения, поэтому достаточно найти значение функции на концах отрезка.

Ответ: наибольшее значение 1, наименьшее -5.

Написать правильный и достоверный ответ;
Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу;
Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.

Применяя эту формулу, зная конкретное значение \(x\), можно вычислить соответствующее значение \(y\).

Чтобы построить график данной функции, нам нужны координаты двух точек, принадлежащих графику функции.

В жизни существует множество ситуаций, которые можно описать математической моделью с помощью линейных функций.

на овощной базе хранится \(700\) т картофеля. Каждый день запасы пополняют на \(30\) т. Сколько картофеля станет на овощной базе через \(2\); \(4\); \(10\) дней?

После \(x\) дней количество \(y\) картофеля на овощной базе можно записать в виде формулы \(y = 700 + 30x\).

Если функцию \(y = kx + m\) надо исследовать только для значений \(x\) из некоторого множества \(X\), то записывают y = kx + m , x ∈ X .

b) Во втором случае функция та же, только значения \(x=-6\) и \(x=3\) не рассматриваются, так как они не принадлежат интервалу \((-6;3)\).

По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.

b) y = 1 3 x + 1, x ∈ − 6 ; 3 , концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.

Наибольшее и наименьшее значения функции на множестве
(основные определения)

Пусть X – некоторое множество, входящее в область определения D ( f ) функции y = f (x) .

Определение 1. Значение f (x₀) функции y = f (x) в точкеназывают наибольшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство

Наибольшее значение функции f (x) на множестве X часто обозначают

Определение 2. Значение f (x₀) функции y = f (x) в точке называют наименьшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство

Наименьшее значение функции f (x) на множестве X часто обозначают

Определение 3. Наибольшее значение функции на множестве X часто называют максимальным значением функции f (x) на множестве X или максимумом функции f (x) на множестве X . Наименьшее значение функции на множестве X часто называют минимальным значением функции f (x) на множестве X или минимумом функции f (x) на множестве X .

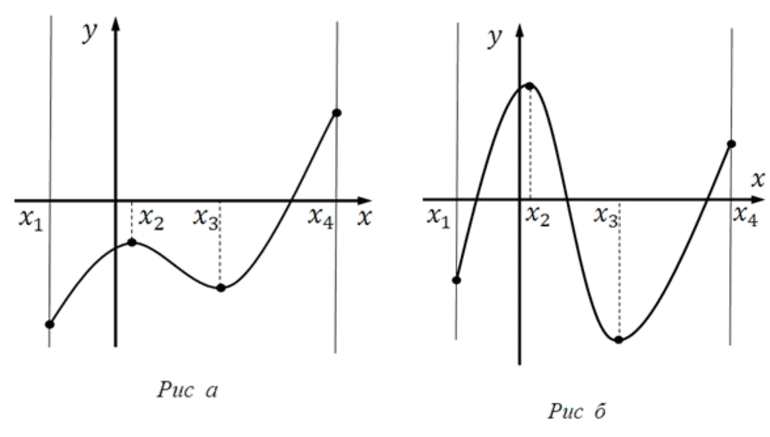
Пример 1. Минимальным значением функции y = x 2 на множестве является число 0 (рис. 1).

Максимального значения функция y = x 2 на множестве не имеет.

Пример 2. Максимальным значением функции y = – x 2 на множестве является число 0 (рис. 2).

Минимального значения функция y = – x 2 на множестве не имеет.

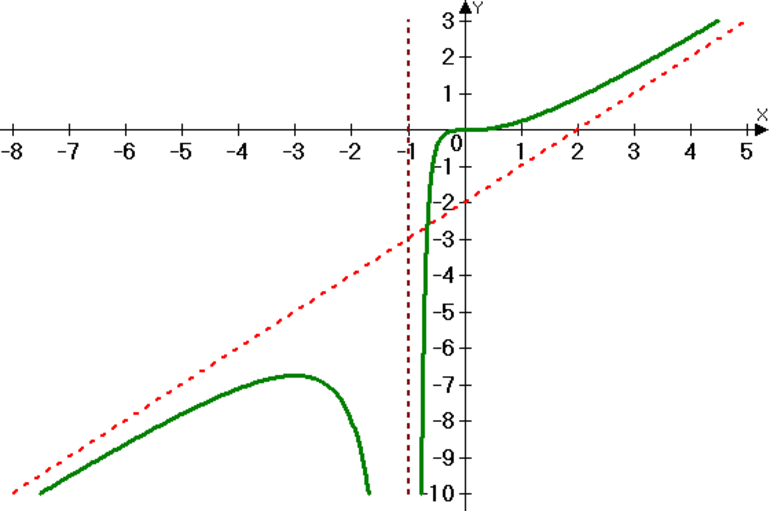
Пример 3. Функция y = x на множестве не имеет ни максимального, ни минимального значений (рис. 3).

Пример 4. Функция y = arctg x на множестве не имеет ни максимального, ни минимального значений (рис. 4).

Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса

Как мы видели в примерах 1 - 4, даже такие хорошо известные функции, как

не имеют наибольших или наименьших значений на множестве. Однако, если бы в качестве множества X мы взяли произвольный отрезок, то ситуация стала бы принципиально иной, что вытекает из следующей теоремы.

Теорема Вейерштрасса. Если функция непрерывна на отрезке, то на этом отрезке существует точка, в которой функция принимает наибольшее значение, а также точка, в которой функция принимает наименьшее значение.

Доказательство теоремы Вейерштрасса выходит за рамки школьного курса математики и здесь не приводится.

Примеры решения задач

y = 2x 3 + 3x 2 – 36x + 30

(1)

Из формулы (2) получаем, что критическими точками функции (1) являются точки x = – 3 , x = 2, причем только точка x = 2 принадлежит отрезку [–2, 4] . Вычисляя значения функции (1) в критической точке x = 2, а также на концах отрезка x = – 2 и x = 4 , получим:

y (2) = – 14 ,

y (– 2) = 98 ,

y (4) = 62 .

Ответ. Наибольшее значение функции (1) на отрезке [–2, 4] равно 98 , а наменьшее значение функции (1) на отрезке [–2, 4] равно – 14 .

на отрезке [–1, 27] .

Решая уравнение y' = 0 , получим

Заметим также, что производная (4) функции (3) не существует в точке x = 0 . Следовательно, у функции (3) есть три критические точки: x = 0, и , причем все эти точки лежат на отрезке [–1, 27] . Вычисляя значения функции (3) в критических точках x = 0, и , а также на концах отрезка x = – 1 и x = 27 , получим:

y (0) = 0 ,

y (– 1) = – 1 ,

y (27) = 99 .

Ответ. Наибольшее значение функции (3) на отрезке [–1, 27] равно 99 , а наменьшее значение функции (3) на отрезке [–1, 27] равно – 1 .

y = (x – 4) e | x |

(5)

Решение. Для того, чтобы найти критические точки функции (5), перепишем правую часть формулы (5), используя определение модуля:

В точке x = 0 производная функции (5) не существует. Критическими точками являются точки

Все критические точки принадлежат отрезку [–1, 6] . Вычисляя значения функции (5) в критических точках x = 0, x = 3, x = 5, а также на концах отрезка x = – 1 и x = 6 , получим:

y (0) = – 4 ,

y (3) = – e 3 ,

y (5) = e 5 ,

y (– 1) = – 5e ,

y (6) = 2e 6 .

Ответ. Наибольшее значение функции (5) на отрезке [–1, 6] равно 2e 6 , а наменьшее значение функции (5) на отрезке [–1, 6] равно – e 3 .

y = (x – 27) e 28 – x

(6)

на отрезке [23, 40] .

В некоторых задачах нужно найти наибольшее и наименьшее значения функции. Если неизвестен алгоритм и основные правила, то простое задание превращается в изнурительный труд, который очень редко приносит положительные результаты. В интернете существует множество информации, но не вся она достоверна. Самое страшное — применение неверных методик нахождения.

Общая информация

Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.

Нахождение области определения функции (ОДФ).
Понятие дифференциала и основные методы его нахождения.
Умение решать уравнения.
Знание графиков простых функций.
Основные типы функций, полуинтервал и интервал.

Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.

Область определения

Обозначение интервалов

Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:

Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.

Зависимость от типа

Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:

Алгебраические: рациональные и иррациональные.
Тригонометрические: sin, cos, tg и ctg.
Трансцендентные: степенные, показательные и логарифмические.

Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.

Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.

Метод нахождения

Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:

Найти корни уравнения знаменателя, приравнивая его к 0.
Определить интервал, значения из которого может принимать аргумент.

В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.

Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.

Для примера нужно разобрать задачу, в которой следует найти D(3x / [(x - 1) * (x + 1) * (10 - x)^(1/2)]). Решать ее необходимо по такому алгоритму:

Знаменатель является сложным. Он состоит из двух выражений: (x - 1) * (x + 1) и (10 - x)^(1/2).
Первое выражение (решить уравнение): (x - 1) * (x + 1) = 0. Оно имеет два корня: x1 = -1 и x2 = 1. Числовой промежуток: (-бесконечность;-1) U (1;+бесконечность).
Второе (неравенство): (10 - x) a). Например, (a;+inf): х = lim [f(x)], где x->a и x->+inf.

Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.

Примеры решений

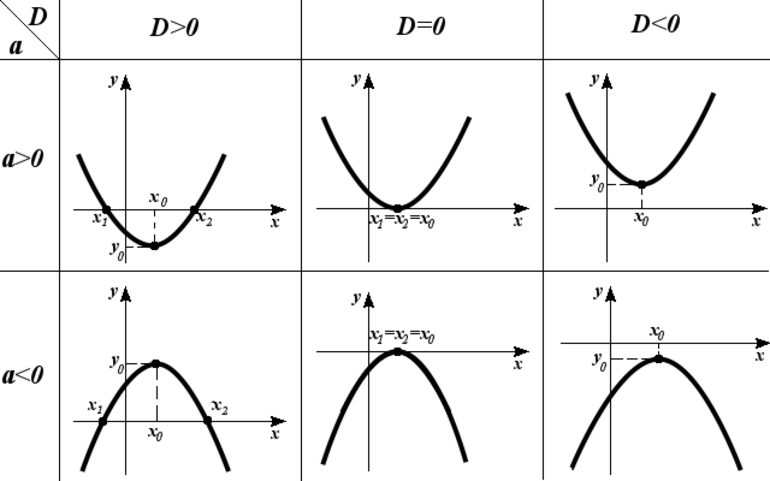
Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:

D(y): все множество Z.
Отрезок входит в D(y).
Производная: y' = [x^2 + 6x + 9]' = 2x + 6 (существует во всех точках).
Стационарные точки (y' = 0): 2x + 6 = 0. Отсюда, x = -3.
Подставить в исходное выражение: y(-3) = (-3)^2 + 6 * (-3) + 9 = 9 - 18 + 9 = 0, y(1) = (1)^2 + 6 * (1) + 9 = 1 + 6 + 9 = 16 и y(5) = (5)^2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
Максимум и минимум (с учетом стационарной точки и интервала): MIN(y) = 0 и MAX(y) = 64.

Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:

D(z) — все значения от бесконечно малого до бесконечно большого чисел.
Промежуток, на котором нужно найти максимум и минимум, полностью входит в D(f).
Дифференциал: z' = 5 (существует во всех точках, а стационарных точек нет вообще).
Минимум и максимум: MIN(z(-3)) = 5 * (-3) + 10 = -5 и MAX(z(3)) = 5 * (3) + 10 = 25.

Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.

Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.

Читайте также: