Метод площадей конспект урока

Обновлено: 02.07.2024

В данной работе рассматривается один из самых распространенных алгоритмов решения геометрических задач – метод площадей. Значимость метода площадей заключается в том, что он является предметом изучения и одновременно средством для изучения последующего материала.

Цель: Рассмотрение теоретических основ;
Формирование представления о методе площадей;
Использование метода площадей при решении планиметрических (второй части ОГЭ и некоторых конкурсных) задач.

Актуальность

II. Основная часть.

1. Метод площадей.

2. Определение метода площадей. Характеристики метода.

3. Основные свойства площадей и ключевые задачи.

4. Практический диапазон применимости метода площадей к решению задач

V. Приложение. Причины ошибок. Классификация

I. Введение

Определение проблемы: необходимость разбора решения геометрических задач из второй части экзаменационной работы по выбранному методу.

1. Изучение научно-методической литературы по проблеме исследования.

Изучение метода площадей и после определения проблемы научиться применять свойства площадей для составления соотношений, связывающих ключевые задачи с неизвестными, используя различные приёмы.

2. Анализ различных учебных пособий с целью изучения и описания метода площадей.

3. Рассмотрение некоторого диапазона применимости метода площадей к решению задач.

4. Рассмотрение на примерах структуры процесса решения таких задач и развитие умения самостоятельно анализировать и конструировать свои знания; классифицировать задачи.

5. Умение ориентироваться в планиметрическом пространстве и нахождение путей решения.

Трудности решения геометрических задач обусловлены следующими факторами:
Неалгоритмичность задач.
Необходимость выбора метода решения задачи и теоремы для решения конкретной задачи из большого набора известных фактов.

Результаты исследования.

Сбор, анализ полученных данных, систематизация решенных задач, корректировка их. Оформление результатов исследовательской работы в электронном виде.

II. Основная часть

1. Метод площадей.

В школьном курсе математики, самыми трудными считаются

геометрические задачи. Как научиться решать геометрические задачи,

особенно сложные, конкурсные? При решении геометрических задач, как

правило, алгоритмов нет, и выбирать наиболее подходящую к данному

случаю теорему не просто.

В данной работе рассматривается один из самых распространенных

алгоритмов решения геометрических задач – метод площадей. Значимость метода площадей заключается в том, что он является предметом изучения и одновременно средством для изучения последующего материала.

Методы решения планиметрических задач. (Дополнительный материал).

Некоторые методы решения геометрических задач (№24, 25, 26)

· Метод дополнительных построений

· Метод вспомогательной окружности.

· Метод площадей

· Также возможно использование векторного способа на плоскости, возможно использование координатного способа. Учащийся не ограничен в выборе метода решения этих задач.

Геометрические задачи повышенной сложности ОГЭ

В работах на примерах решения конкретных задач обычно используются такие методы:

1. Удвоение медианы

2. Использование введения буквенных обозначений величин

3. Метод вспомогательных построений

4. Построение вспомогательных отрезков в трапеции

5. Использование осевой симметрии

6. Переход к равновеликой вспомогательной фигуре

7. Метод площадей.

8. Введение вспомогательной окружности.

(См. в презентации ключевые задачи)

4. Построение вспомогательных отрезков в трапеции

5. Использование осевой симметрии

6. Переход к равновеликой вспомогательной фигуре

7. Метод площадей.

8. Введение вспомогательной окружности.

(См. в презентации ключевые задачи)

Рассмотрим в нашем исследовании метод площадей.

2. Определение метода площадей. Характеристики метода.

Из названия следует, что главным объектом данного метода является площадь.

Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры.

1. Весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное.
Здесь и проявляется основная особенность метода площадей:
из геометрической задачи он "делает" её алгебраической, сводя всё к решению уравнения (а иногда и системы уравнений).

2. Одна из разновидностей метода площадей сводится к использованию в задаче свойства аддитивности площади: если фигура разбита на части, то ее площадь равна сумме площадей этих частей. S=S1+S2+S3

2. Универсального метода для решения всех задач на площади

многоугольников нет, но существуют приемы, применимые ко многим

задачам. Понятие площади мы используем даже при решении тех задач,
в условии которых отсутствует упоминание площади. Поэтому можно

говорить о методе площадей в геометрии.

4. Метод площадей состоит в применении различных её свойств для нахождения соотношений, связывающих их с неизвестными.

Остановимся подробнее на характеристике и диапазоне применимости метода площадей.

3. Основные свойства площадей

Свойство 1. Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться.

Рассмотрим ▲ABC и ▲ADC. Они

имеют общее основание и равные

высоты, т.к. прямые AC и BD

параллельные, то расстояние между

ними равно h - высоте ▲ABC и ▲ADC.

Свойство 2. Если два треугольника имеют одинаковые высоты, то отношение их

площадей равно отношению длин оснований, т. е. сторон,
на которые опущены эти высоты.

Пусть h1 = h2 в двух треугольниках

с основаниями a и b.

Рассмотрим отношение площадей

этих треугольников, получим:

Если два треугольника имеют общий угол, то их площади относятся

как произведение сторон, заключающих этот угол.

Рассмотрим ▲ABC и ▲MBN.

Пусть AB = k∙MB, BC = k∙NB и ABC=MBN .

Используя формулу площади треугольника, получим: отношение подобных площадей ▲ABC и ▲MBN.

Тогда получим: = k 2 .

Медиана треугольника делит его на две равновеликие части.

Рассмотрим ▲ABC . Пусть

медиана - BM , тогда

AM=MC=1/2AC. Медиана делит

треугольник на два равновеликих с одинаковой

высотой. Найдем площади

Медианы треугольника делят

его на три равновеликие части.

Медианы треугольника делят его
на 6 равновеликих частей.

Утверждение. Два треугольника
являются равновеликими,

если равны их высоты и основания.

Средние линии треугольника площади S

отсекают от него

треугольники площади ¼ S.

Рассмотрим ▲ABC. NM - средняя линия

в треугольнике и она равна половине

Если SABC = S, то можно доказать, что

площади всех треугольников равны

одной четвертой части площади ▲ABC.

4. Применение свойств метода площадей к решению задач.

В данном пункте рассмотрим систему геометрических задач, решаемых методом площадей. Задачи построены по нарастающему уровню сложности.

№1( Задания типа № 24).

Стороны AC, AB, BC треугольника ABC равны 2 , и 2 соответственно. Точка K расположена вне треугольника ABC , причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠ KAC > 90°. Найти площадь треугольника АВС.

Рассмотрим подобные треугольники ABC и AKC и установим соответствие между их углами. Против большей стороны всегда лежит больший угол, в треугольнике ABC это угол ABC в треугольнике , в свою очередь, есть тупой угол и он является наибольшим, значит, ∠ КАС = ∠ АВС. Угол АСК заведомо не может быть равен углу так как он составляет только его часть. Следовательно, угол АСВ равен углу АКС.

Найдём косинус угла , используя теорему косинусов:

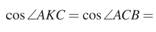
Найдём: = ; ) 2 = = = . S _ABC =

Задания типа № 25.

№2. В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.

Проведём высоту так, чтобы она проходила через точку О. Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно, эти треугольники равны, а значит, равны отрезки и . Таким образом,

Площадь параллелограмм равна а площадь треугольника

В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 10 : 9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABС.

Пусть площадь треугольника равна

Проведём прямую параллельную Точка — середина следовательно, — средняя линия треугольника значит,

По теореме Фалеса для угла находим:

а так как получаем, что

Стороны треугольников и сонаправлены, их площади относятся как произведение отношений сонаправленных сторон,
поэтому

откуда , в то время как следовательно,

Тем самым, для искомого отношения площадей имеем:.

Олимпиадные задачи: 9 класс.

1. Сторона KP трапеции NMКP равна 3 см. Расстояние из вершин N и М до стороны КР равны 7см и 5 см соответственно. Найдите площадь трапеции NMКP.

Решение. Сделаем чертеж. Опустим перпендикуляры из точек N и М на сторону КР и построим перпендикуляр KH к стороне NP .

Обозначим ∠ ANP через α. Заметим, что ∠ BMK = ∠ ANP = α (стороны этих углов соответственно параллельны), а также ∠ HKP = ∠ ANP = α (в прямоугольных треугольниках NAP и KHP угол с вершиной Р– общий).Тогда имеем три подобных прямоугольных треугольника: NAP, MВK и КНР.

Значит: МК= , NP= , КH= . Следовательно,

S_NMKP = ( MK + NP ) KH = = 18 (кв.см). Ответ: 18 кв.см

а) В треугольнике АВС на продолжении медианы ВМ выбрана точка К так, что МК:ВМ = 1:2. Известно, что АВ=5, ВС=3, СК=4. Найти АК.

б) Найти площадь треугольника АВС.

Решение. Сделаем чертёж:

Обозначим ∠ АМК через α. Тогда ∠ АМВ = π-α, ∠ ВМС = α, ∠ СМК = π-α.

Применим теорему косинусов к треугольникам АВМ, ВСМ, СКМ и АКМ.

КМ= х, тогда ВМ= 2х, АМ =СМ= у.

25= у 2 +4х 2 +4ху cosα ,

9= у 2 +4х 2 - 4ху cosα ,

16 = у 2 + х 2 +2ху cosα .

Решив систему трёх уравнений с тремя неизвестными, получим:

Из треугольника АКМ имеем: АК 2 = 12-2 . Тогда АК=2 .

б) Найти площадь треугольника АВС.

S_ABC = • 2• MB • MC • ; ∠ ВМС = α; ; =

1. При решении геометрических задач внимательно анализировать условие задачи, находить взаимосвязь между элементами геометрических фигур, применять свойства и конкретные приёмы решения задач.

2. Использовать приравнивание выражений, полученных по различным формулам площади для одной и той же фигуры, что позволит получить зависимость между ее элементами. Полезно рассматривать отношение площадей фигур, одна из которых (или обе) содержит в себе искомые элементы.

4. Для развития умений самостоятельно конструировать свои знания, рассматривая различные структуры процесса решения задач, ориентируясь в информационном и социальном пространстве.

Подводя итог обзору методов решения и методов поиска решения геометрических задач, заметим, что не все этапы в равной степени обязательно присутствуют в решении любой задачи. Мы рассмотрели примеры, показывающие, что не всегда приходится выявлять характерные особенности конфигурации и, наоборот, некоторые решения одним этим этапом, по сути, и исчерпывались. Отдельно следует сказать об анализе полученного решения. Основная функция анализа - контроль правильности полученного решения,

Иногда в ходе анализа необходимо провести исследование, существует ли полученная конфигурация, не относится ли она к разряду невозможных, при каких условиях возможно ее существование.

Изучение методов решения геометрических задач будет более эффективным, если рассматривать на примере одной задачи возможности использования

различных геометрических приёмов.

1. Причины ошибок в решении геометрических задач

· Незнание и/или непонимание аксиом, определений, теорем

· Неумение их применять

· Невнимательное чтение условия и вопроса задания

· Нарушения логики в рассуждениях

· Принятие ошибочных гипотез. Недостатки в работе с рисунком.

2. Классификация задач, решаемых методом площадей

1. В условии задачи упоминается о площади
2. В условии задачи не упоминается о площади

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Муниципальное общеобразовательное учреждение – гимназия № 1

Урок геометрии в 11 классе

Тема: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ

Автор: Дацко Елена Владимировна

учитель математики

г. Клин, 2014 год

2.3. Работа на уроке по вариантам с различной сложностью……………………………..7 – 9

2.4. Самостоятельная работа контролирующего характера……………………………10 – 11

2.5. Итог урока. Домашнее задание с подробным разбором задач. ……………….…11 – 17

Цель урока: повторение и обобщение знаний о методе площадей в решении задач.

– обучающие: обобщить и систематизировать знания о методе площадей, отработать умения применить формулы в решении задач.

– развивающие: развить познавательные умения,

– воспитательные: развить положительное отношение к знаниям.

Тип урока: урок повторения.

I . Актуализация знаний.

Площади треугольников, имеющих равные высоты (общую высоту), относятся как стороны соответствующие этим высотам.

Площади треугольников, имеющих равные стороны, относятся как соответствующие этим сторонам высоты.

Площади треугольников, имеющих равный угол (или общий угол), относятся как произведение сторон, содержащий этот угол.

Медиана делит треугольник на два равновеликих треугольника.

Три медианы треугольника делят его на шесть равновеликих треугольников.

II . Устная работа.

Слайд 8 Случай, когда треугольники имеют общую высоту.

имеют общую высоту

Решение: имеют общую высоту

1) Отношение площадей треугольников, имеющих общую высоту равно отношению сторон, к которым проведена высота.

2) Если же стороны, к которым проводится высота равны, то и площади треугольников также равны.

3) Во сколько раз отношение сторон треугольников, к которым проводится высота больше (меньше), во столько раз и площади больше (меньше).

Случай, когда треугольник и параллелограмм имеют общую высоту.

Вывод: В этом случае отношение площадей треугольника и параллелограмма равно отношению их высот. Высота параллелограмма есть высота треугольника. Но в нахождении площади треугольника присутствует коэффициент , а, значит, составляя и решая данную пропорцию, получаем 8.

(Отношение площадей, имеющих общий угол равно отношению произведения сторон, заключающих данный угол).

III . Работа на уроке.

1 ряд. Работа в парах (сидят слабый ученик и ученик средних способностей).

I вариант

1) Найдём какую часть составляет от

II вариант

1) (сторона – общая),

2) Дополнительное построение

По теореме Фалеса – средняя линия,

3) подобен (по двум углам),

4) по свойству медиан

подставим в получим

IV . Самостоятельная работа контролирующего характера (дифференцированная).

I вариант

Параллелограмм и имеют общую сторону

II вариант

имеют общую высоту, значит их площади

V . Итог урока.

Домашнее задание. Ученику следует выбрать для решения две любые задачи. При желании можно выполнить всё задание.

Задача 1. В треугольнике со сторонами вписан параллелограмм причём точки лежат на сторонах соответственно. Известно, что площадь параллелограмма составляет площади треугольника Найдите стороны параллелограмма.

4) подобен по двум углам.

как накрест лежащие,

Ответ: 12 и 4 или 6 и 8.

Другой способ решения данной задачи:

Ответ: 6 и 8 или 12 и 4.

Задача 2. В треугольнике _{на прямой} _{выбрана точка} _{так, что} _Точка _{середина стороны} _Прямая _{пересекает отрезок} _{в точке} _{Найдите площадь треугольника} _{если площадь треугольника} _{равна 120.}

2) общая высота, общая высота.

Задача 3. Через точку лежащую в треугольнике проведены три прямые, параллельные всем сторонам треугольника. В результате треугольник разбился на 3 треугольника и 3 параллелограмма. Известно, что площади полученных треугольников равны соответственно 1;2,25и 4. Найдите сумму площадей полученных параллелограммов.

$F:\333.jpg$

Задача 4. Площадь трапеции равна 810. Диагонали пересекаются в точке

Отрезки, соединяющие середину основания с вершинами и пересекаются с диагоналями трапеции в точках и Найдите площадь треугольника если одно из оснований трапеции вдвое больше другого.

$F:\111.jpg$

1) Рассмотрим четырёхугольник основания трапеции. параллелограмм.

2) по двум сторонам и углу между ними. Аналогично, Значит,

3) диагонали параллелограмма делят его на четыре равных по площади треугольника.

4) Т. к. то средняя линия треугольника

$F:\222.jpg$

Пусть высота трапеции.

Треугольник подобен треугольнику с коэффициентом а треугольник подобен треугольнику с коэффициентом Тогда

1. Геометрия. 10 – 11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 22-е изд. – М.: Просвещение, 2013. – 255с.

2. Геометрия в таблицах. 7 – 11 кл.: Справочное пособие / Авт.-сост. Л.И. Звавич, А.Р. Рязановский. – 4-е изд., стереотип. – М.: Дрофа, 2000. – 128 с.

Краткое описание документа:

Обобщающий урок геометрии закрепляет теоретические знания и практические навыки решения планиметрических задач методом площадей. Материалы занятия дифференцированы по уровням сложности и адаптированы для групп учащихся с разными способностями. даны условия задач с подробным разбором решения.

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 933 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 683 человека из 75 регионов

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

Курс добавлен 31.01.2022
Сейчас обучается 24 человека из 17 регионов

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 611 075 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

08.05.2015 1076
DOCX 849.3 кбайт
3 скачивания
Оцените материал:

Настоящий материал опубликован пользователем Дацко Елена Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Курские власти перевели на дистант школьников в районах на границе с Украиной

Время чтения: 1 минута

Время чтения: 2 минуты

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Время чтения: 0 минут

Рособрнадзор предложил дать возможность детям из ДНР и ЛНР поступать в вузы без сдачи ЕГЭ

Время чтения: 1 минута

В Россию приехали 10 тысяч детей из Луганской и Донецкой Народных республик

Время чтения: 2 минуты

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Урок позволит обобщить и систематизировать знания о методе площадей, отработать умения применить формулы в решении задач.

Описание разработки

Цель урока:

повторение и обобщение знаний о методе площадей в решении задач.

Задачи:

обучающие: обобщить и систематизировать знания о методе площадей, отработать умения применить формулы в решении задач.

развивающие: развить познавательные умения,

воспитательные: развить положительное отношение к знаниям.

Ход урока.

I. Актуализация знаний.

Площади треугольников, имеющих равные стороны, относятся как соответствующие этим сторонам высоты.

В школьном курсе математики, самыми трудными считаются геометрические задачи. Как научиться решать геометрические задачи, особенно сложные, конкурсные? При решении геометрических задач, как правило, алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не просто. Поэтому, желательно в каждой теме выработать какие-то общие положения, которые полезно знать всякому решающему геометрические задачи.

В данной работе рассматривается один из самых распространенных алгоритмов решения геометрических задач – метод площадей, т.е. решение задач с использованием свойств площадей.

Вложение	Размер
metod_ploshchadey.pdf	722.28 КБ

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Использование различных методов при решении геометрических задач на нахождение углов и расстояний между плоскостями и прямыми в пространстве.

Приведу необходимые теоретические знания, позволяющие успешно решать геометрические задачи группы С(С2) ЕГЭ – 2011, 2012гг. Теоретические положения упорядочены и акцентированы именно на решение .

Данный спецкурс рассчитан на 34 часа. Его основная цель познакомить учащихся с некоторыми методами и приемами решения задач по геометрии, научить выделять в них общие подходы , научи.

Решение геометрических задач "Методом площадей"

Координатные методы решения геометрических задач

Данная работа представляет собой набор задач и необходимый для их решения теоретический материал. Работе с координатными и векторными методами решения задач в курсе общеобразовательной школы зачастую .

Использование метода ассоциаций в решении геометрических задач (из опыта подготовки выпускников к ОГЭ по математике)

В статье обобщен опыт использования метода ассоциаций в обучении математике.

Практическое занятие: ПРИМЕНЕНИЕ ВЕКТОРОВ И МЕТОДА КООРДИНАТ К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ

При вычислениях надо использовать инженерный калькулятор.

Выработка умения анализировать и сравнивать различные геометрические объекты: формулы, геометрические фигуры.

Читайте также: