Графическое решение уравнений и неравенств конспект

Обновлено: 04.07.2024

1) Найти область определения уравнения, то есть область допустимых значений неизвестного и параметра, при которых уравнение может иметь решение;

2) Выразить параметр а как функцию от х: а = f(х);

3) В системе координат построить график функции а= f(х) для тех значений х, которые входят в область определения;

4) Определить точки пересечения прямой а = с с графиком функции а = f(х).

а) прямая а = с не пересекает график а = f(х). Уравнение решений не имеет;

b) прямая а=с пересекает график а = f(х) в одной или нескольких точках. Определяем абсциссы точек пересечения, решая уравнение а = f(х) относительно х.

Задание 1

Решить уравнение х² ‒ (2х ‒ 1) = а

1) Область определения уравнения: х є R, а є R.

2) Если х >1/2, то а = х² ‒ 2х +1 или а = (х ‒ 1)²

Если х 1/2 и а = (х +1)² ‒ 2, при х ¼ имеет х1 = ‒1 ‒√а + 2, х2 = 1 + √а

Задание 2

При каких значениях параметра a уравнение ((х ‒ 4) ‒3) + 2а = 0 имеет три решения. Найти эти решения.

Преобразуем уравнение к виду: ((х ‒ 4) ‒ 3)= ‒2а;

Сначала строим график ((х ‒ 4) ‒3), полученный из графика y = (х)

Перемещаем вдоль оси Ох на 4 единицы, вдоль оси Оy на (‒3) единицы и зеркальным отображением отрицательной части графика относительно оси Ох, так как у > 0 по свойству модуля.

Далее график y = ‒2а (Рис. 7) ‒ прямую линию, параллельною оси Ох перемещаем вдоль оси Оу до тех пор, когда она пересечёт первый график в трёх точках.

Получим ‒ 2а = 3, а = ‒1,5.

Ответ: при а = ‒1,5 уравнение имеет три решения: х1 = ‒ 2а; х2 = 4;

Задание 3

При каких значениях параметра a уравнение (х² ‒ 8 ‧ (х) +15) = а имеет ровно 6 корней.

Построим график функции у = ( х² ‒ 8 ‧ (х) +15) (Рис. 8).

График функции у=а представляет собой множество прямых, параллельных оси абсцисс. Он будет пересекать график функции

у = (х² ‒ 8 ‧ (х) + 15) в 6 точках при а = 1, а значит, исходное уравнение имеет 6 корней при а = 1.

2.2. Графический метод решения уравнений

Прямоугольная система координат используется при графическом методе решения уравнений. Графический метод решения уравнений позволяет определить число корней уравнения, угадать значение корня, грубо указать отрезки на числовой оси, где они могут находиться.

Графический метод заключается в следующем. Рассматривается уравнение с одним неизвестным f1 (х) = f2 (х). Строятся графики функций у1 = f1(х) и у2 = f2(х) (Рис. 9).

Точки пересечения графиков этих функций соответствует тем значениям аргумента х, при которых совпадают значения функций, то есть решениям (корням) уравнения.

Задание 1

Найти число корней уравнения √х = (х ‒ 1)² и указать отрезки на числовой оси, где они могут находиться.

Построим графики функций у =√х и у = (х ‒ 1)² (Рис. 10).

Из рисунка видно, что уравнение имеет два корня, один из которых находится в интервале (0; 1), а другой ‒ в интервале (2; 3).

Задание 2

Сколько решений имеет уравнение x²/cosx - 10 = 0

Перепишем уравнение в виде x²/10 = cos х.

Построим графики функций у = x²/10 и у = cos х (Рис. 11).

Из рисунка видно, что уравнение имеет два решения.

2.3. Графический метод решения неравенств

Для успешного решения задач повышенной сложности важно уметь строить не только графики функций, но и множество точек плоскости, координаты которых удовлетворяют заданным неравенствам и их системам. Эффективно строить на координатной плоскости такие множества позволяет метод областей.

Неравенство с двумя неизвестными можно представить так: f (х, у) > 0. Если мы рассмотрим уравнение f (х, у) = 0, то можно построить его геометрическое изображение. Это будет кривая, которая разбивает плоскость на две или несколько областей. В каждой из этих областей функция сохраняет знак, остается выбрать те из них, в которых f (х, у) >0. Многие практические задачи сводятся к системам двух или нескольких линейных неравенств с двумя неизвестными х и у. Система линейных неравенств может иметь бесконечное множество решений, может иметь только одно решение, может не иметь решений.

Задание 1

Сколько решений имеет система неравенств:
x+y>4
x-y -9

Изобразим в прямоугольной системе координат решение каждого неравенства системы (Рис. 12).

Из рисунка видно, что данная система имеет бесконечное множество решений - внутренность треугольника.

Задание 2

Сколько решений имеет система неравенств:
x+y>=0
x+3y 0

Сначала построим графики функций у = -2/3х + 2 и у = х² ‒ 1
(Рис. 14).

Решением первого неравенства является интервал х >3, обозначенный черной стрелкой; решение второго неравенства состоит из двух интервалов: х 1, обозначенных серыми стрелками.

Из графика видно, что пересечением этих двух решений является интервал х > 3.

Это и есть решение заданной системы неравенств.

2.4 Построение фигуры в системе координат с помощью отрезков графиков линейных функций

Так как все функции линейны, то их графики имеют вид отрезков прямых и следовательно, однозначно определяются концевыми точками. Получаем рисунок (Рис. 15).

Можно построить рисунок по координатам. Получаем рисунок утёнка (Рис. 16).

Модовскопошатская общеобразовательная средняя школа им. В. В. Кирдяшкина.

Тип урока: комбинированный.

систематизировать, расширить и углубить знания и умения учащихся по теме графический способ решения уравнений и неравенств;

способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы;

развивать умения учащихся применять полученные знания на практике;

побуждать учеников к самоконтролю, вызывать у них потребность в обосновании своих высказываний.

I. Организационный момент.

II. Фронтальный опрос.

1). Назовите формулы функции, известных вам? (Слайд 3 )

2). Что служит графиком функции?

y = kx + b ; у=ах +вх +с ; у= ; у = ; у= .

3) Как построить график функции у = f(х +l) +m, если известен график функции у = f(х)?

4) Назовите формулу функции, график которой изображен на рисунке

Графиком называется множество точек координатной плоскости, у которых значения x и y связаны некоторой зависимостью и каждому значению x соответствует единственное значение y.

Графический способ - один из самых удобных и наглядных способов представления и анализа информации.

Например, метеорологическая служба фиксирует изменения температуры, строя с помощью термографа (специального прибора, отмечающего температуру на движущейся ленте или экране дисплея) график температуры.

Используя показания сейсмографов (приборов непрерывно фиксирующих колебания почвы и строящих специальные графики- сейсмограммы) геологи могут предсказать приближение землетрясения или цунами. (Слайд 9).

Врачи выявляют болезни сердца, изучая графики, полученные с помощью кардиографа, их называют кардиограммы. (Слайд 10).

Струя, как траектория движения всякого тела, брошенного под углом а к горизонту, имеет форму параболы, тем более вытянутой, чем больше начальная скорость. (Слайд 11)

Закон Бойля – Мариотта описывает количественную зависимость давления от объема газа. Графиком его является часть дуги одной из веток гиперболы. (Слайд 12)

Широко применяются графики в экономике, в частности кривая спроса и предложения, линия производственных возможностей.

IV. Выполнение упражнений

На практике довольно часто оказывается полезным графический метод решения уравнений. Он заключается в следующем: для решения уравнений f(x)=0 строят график функции y=f(x) и находят абсциссы точек пересечения графика с осью Оx: эти абсциссы и являются корнями уравнения. (Слайд13)

Алгоритм решения уравнений графическим способом

(ученики формулируют сами)

Чтобы решить графически уравнение вида f(х) = g(х), нужно:

1.Построить в одной координатной плоскости графики функции:

2. Найти точки пересечения этих графиков.

3. Указать абсциссу каждой из этих пересечения.

4. Записать ответ. ( Слайд 14)

Задача № 20.31 (в; г) Решить графически уравнение:

в) х (решение у доски и в тетрадях);

г) (один ученик решает на компьютере, а затем спроектировав его решение на экран проверяется правильность решения задания).(слайд 15)

Довольно просто решать графически систему уравнений, так как каждое уравнение системы на координатной плоскости представляет какую- то линию. (слайд16)

Построив графики этих уравнений и найдя координаты точек их пересечения (если они существуют), мы получим искомое решение.

Как построить график функции у=-х²-2 и 5х-3у=0.

Решить самостоятельно, проверить с помощью слайда 17.

Графическое решение неравенств, сводится к отысканию таких точек x, при которых один график лежит выше или ниже другого

Задача №20.42(а). Решить неравенство х+2≤-х²+4.

Решение на доске и в тетрадях. (слайд18)

Решение прикладной задачи (Слайд 19)

V. Проверочная самостоятельная работа по карточкам

(второе задание дополнительное).

1.Решите графически уравнение .

2.Сколько корней имеет уравнение .

1.Решите графически уравнение .

2. Сколько корней имеет уравнение - .

1.Решите графически уравнение

2. Сколько корней имеет уравнение х .

Каждому ученику выдается листок с заданиями . Проверку выполнения заданий можно осуществить, спроектировав их решения на экран. Обратить внимание учащихся на то, что уравнение относится к иррациональным, которые изучаются в 9 классе, а вы можете их решать пока графически.(Слайды 20-22)

Домашнее задание: №20.32(а), 20.37(в), 22.40(а).

Графическим методом легко решаются некоторые уравнения с параметром, например, при каких значениях р уравнение lx+2l-3=р имеет один корень, два корня, не имеет корней?

Построим график функции у=lx+2l-3 и прямой у=р и по графику ответим на вопросы. (слайд 23)

Решение задачи (ЕГЭ, С ) (слайд 24)

По теме: методические разработки, презентации и конспекты

Целью урока является совершенствование навыков решения уравнений и неравенств с модулем. В ходе урока рассматриваются рациональные приёмы и методы решения. Урок предназначен для классов с .

Решение уравнений и неравенств с параметрами

Методика решений уравнений и неравенств с параметрами. Можно использовать на факультативных занятиях и при подготовки к ЕГЭ (часть С).

Элективный курс по алгебре 11 класс "Решение уравнений и неравенств"

Рабочая программа элективного курса по алгебре 11 класс.

Программа элективного курса "Решение уравнений и неравенств с модулем."

Элективный курс для 10 классов.

Урок по теме "Решение уравнений и неравенств с параметром"

9-й класс. Урок по теме "Решение уравнений и неравенств с параметром"Чехолкова Алла ВладимировнаЦель: Выработка навыка решения уравнений и неравенств с параметром различными способами. Разв.

Применение свойств функций к решению уравнений и неравенств

Работа посвящена одному из нестандартных методов решения уравнений и неравенств основанному на свойстве ограниченности функций, входящих в уравнение (неравенство). Предлагаемые мной задачи можно рассм.

Использование метода мажоранта при решении уравнений и неравенств

При решении нестандартных задач встречаются уравнения, содержащие разнородные функции, решение которых бывает несложным, если использовать свойства числовых функций.

Многие задания, которые мы привыкли вычислять чисто алгебраически, можно решить намного легче и быстрее!

С помощью графиков функций!

Приступим? Начнем с решения уравнений!

Решение уравнений и неравенств с помощью графиков — коротко о главном

Выразим 𝑥 через 𝑦
Определим тип функции
Построим графики получившихся функций
Найдем точки пересечения графиков
Корректно запишем ответ (с учетом ОДЗ и знаков неравенств)
Проверим ответ (подставим корни в уравнение или систему)

Решение уравнений с помощью графиков

Решение линейных уравнений

Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.

Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.

Сейчас же я покажу тебе, как это сделать графическим способом.

Итак, у тебя есть уравнение: $ \displaystyle 2 -10=2$

Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:

Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.

Иными словами, у нас будет:

А теперь строим. Что у тебя получилось?

Как ты думаешь, что является корнем нашего уравнения? Правильно, координата $ \displaystyle x$ точки пересечения графиков:

Наш ответ: $ \displaystyle x=6$

Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число $ \displaystyle 6$!

Вариант 2

Как я говорила выше, это самый распространенный вариант, приближенный к алгебраическому решению, но можно решать и по-другому. Для рассмотрения альтернативного решения вернемся к нашему уравнению:

$ \displaystyle 2 -10=2$

В этот раз не будем ничего переносить из стороны в сторону, а построим графики напрямую, так, как они сейчас есть:

Что является решением на этот раз? Все верно. То же самое: координата $ \displaystyle x$ точки пересечения графиков:

И снова наш ответ: $ \displaystyle x=6$.

Как ты видишь, с линейными уравнениями все предельно просто. Настало время рассмотреть что-нибудь посложнее… Например, графическое решение квадратных уравнений.

Решение квадратных уравнений

Итак, теперь приступим к решению квадратного уравнения. Допустим, тебе нужно найти корни у этого уравнения:

Конечно, ты можешь сейчас начать считать через дискриминант, либо по теореме Виета, но многие на нервах ошибаются при умножении или возведении в квадрат, особенно, если пример с большими числами, а калькулятора, как ты знаешь, у тебя на экзамене не будет…

Поэтому давай попробуем немного расслабиться и порисовать, решая данное уравнение.

Графически найти решения данного уравнения можно различными способами. Рассмотрим различные варианты, а уже ты сам выберешь, какой больше всего тебе понравится.

Вариант 1. Напрямую

Просто строим параболу по данному уравнению: $ \displaystyle ^>+2 -8=0$

Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:

$ \displaystyle x=-\frac$

Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!

Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:

Точно такой же ответ? Молодец!

И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, $ \displaystyle 3$.

Ты знаешь, что парабола симметрична относительно своей вершины, например:

Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:

Возвращаемся к нашей параболе.

Для нашего случая точка $ \displaystyle A\left( -1;-9 \right)$. Нам необходимо еще две точки, соответственно, $ \displaystyle x$ можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?

Мне удобней работать с положительными, поэтому я рассчитаю при $ \displaystyle x=0$ и $ \displaystyle x=2$.

При $ \displaystyle x=0$:

При $ \displaystyle x=2$:

Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:

Как ты думаешь, что является решением уравнения?

Правильно, точки, в которых $ \displaystyle y=0$, то есть $ \displaystyle x=2$ и $ \displaystyle x=-4$. Потому что $ \displaystyle ^>+2 -8=0$.

И если мы говорим, что $ \displaystyle y=^>+2 -8$, то значит, что $ \displaystyle y$ тоже должен быть равен $ \displaystyle 0$, или $ \displaystyle y=^>+2 -8=0$.

Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!

Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.

Что у тебя получилось? То же самое?

Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!

Вариант 2. С разбивкой на несколько функций

Возьмем все тоже наше уравнение: $ \displaystyle ^>+2 -8=0$, но запишем его несколько по-другому, а именно:

Можем мы так записать? Можем, так как преобразование равносильно. Смотрим дальше.

Построим отдельно две функции:

Построил? Сравним с тем, что вышло у меня:

Соответственно, решением данного уравнения являются:

Что скажешь? Согласись, этот способ решения намного легче, чем предыдущий, и даже легче, чем искать корни через дискриминант!

А если так, попробуй данным способом решить следующее уравнение.

Что у тебя получилось? Сравним наши графики:

$ \displaystyle _>=2^>$
$ \displaystyle _>=5 -3$

По графикам видно, что ответами являются:

Теперь посмотрим уравнения чууууть-чуть посложнее, а именно решение смешанных уравнений, то есть уравнений, содержащих функции разного вида.

Решение смешанных уравнений

Теперь попробуем решить следующее уравнение:

Конечно, можно привести все к общему знаменателю, найти корни получившегося уравнения, не забыв при этом учесть ОДЗ, но мы попробуем решить графически, как делали во всех предыдущих случаях.

В этот раз давай построим 2 следующих графика:

$ \displaystyle _>=\frac$ – графиком является гипербола
$ \displaystyle _>= -2$ – графиком является прямая, которую ты легко построишь, прикинув значения $ \displaystyle x$ и $ \displaystyle x$ в голове, даже не прибегая к калькулятору.

Осознал? Теперь займись построением.

Вот что вышло у меня:

Глядя на этот рисунок, скажи, что является корнями нашего уравнения $ \displaystyle \frac-x+2=0$?

Правильно, $ \displaystyle _>=-1$ и $ \displaystyle _>=3$. Вот и подтверждение:

Попробуй подставить наши корни в уравнение. Получилось?

При $ \displaystyle _>=-1:\frac-\left( -1 \right)+2=-3+1+2=0$.

Все верно! Согласись, графически решать подобные уравнения – одно удовольствие!

Попробуй самостоятельно графическим способом решить уравнение:

Даю подсказку: перенеси часть уравнения в правую сторону, чтобы с обоих сторон оказались простейшие для построения функции. Намек понял? Действуй!

Теперь посмотрим, что у тебя вышло:

$ \displaystyle 2^>=x+1$, соответственно:

$ \displaystyle _>=2^>$ – кубическая парабола.
$ \displaystyle _>=x+1$ – обыкновенная прямая.

Как ты уже давно у себя записал, корнем данного уравнения является $ \displaystyle _>=1$.

Прорешав такое количество примеров, уверена, ты понял, как можно легко и быстро решать уравнения графическим путем. Настало время разобраться, как решать подобным способом системы.

Решение систем уравнений с помощью графиков

Графическое решение систем, по сути, ничем не отличается от графического решения уравнений.

Мы будем строить два графика, и их точки пересечения будут являться корнями данной системы.

Один график – одно уравнение, второй график – другое уравнение. Все предельно просто!

Начнем с самого простого – решение систем линейных уравнений.

Решение систем линейных уравнений

Допустим, у нас есть следующая система:

Для начала преобразуем ее таким образом, чтобы слева было все, что связано с $ \displaystyle y$, а справа – что связано с $ \displaystyle x$. Иными словами, запишем данные уравнения как функцию в привычном для нас виде:

А теперь просто строим две прямые. Что в нашем случае является решением? Правильно! Точка их пересечения! И здесь необходимо быть очень-очень внимательным! Подумай, почему?

Намекну: мы имеем дело с системой, в системе есть и $ \displaystyle x$, и $ \displaystyle y$… Смекаешь?

Все верно! Решая систему, мы должны смотреть обе координаты, а не только $ \displaystyle x$, как при решении уравнений!

Еще один важный момент – правильно их записать и не перепутать, где у нас значение $ \displaystyle x$, а где значение $ \displaystyle y$ !

Записал? Теперь давай все сравним по порядку:

И ответы: $ \displaystyle x=1$ и $ \displaystyle y=-1$. Сделай проверку – подставь найденные корни в систему и убедись, правильно ли мы ее решили графическим способом?

Все сошлось? Идем дальше!

Решение систем нелинейных уравнений

А что если вместо одной прямой, у нас будет квадратное уравнение? Да ничего страшного! Просто ты вместо прямой построишь параболу! Не веришь? Попробуй решить следующую систему:

Какой наш следующий шаг? Правильно, записать так, чтобы нам было удобно строить графики:

А теперь так вообще дело за малым – построил быстренько и вот тебе решение! Строим:

Графики получились такими же? Теперь отметь на рисунке решения системы и грамотно запиши выявленные ответы!

Все сделал? Сравни с моими записями:

При $ \displaystyle _>=-1$, $ \displaystyle _>=0$.

При $ \displaystyle _>=2$, $ \displaystyle _>=-3$.

Все верно? Молодец! Ты уже щелкаешь подобные задачи как орешки! А раз так, дадим тебе систему посложнее.

Решите систему уравнений: $ \displaystyle \left\< \beginy=^>+2x+2;\\y-^>=2.\end \right.$

Что мы делаем? Правильно! Записываем систему так, чтобы было удобно строить:

Итак, поехали! Выдохнул? Теперь начинай строить!

Ну как? Красиво? Сколько точек пересечения у тебя получилось? У меня три! Давай сравнивать наши графики:

Так же? Теперь аккуратно запиши все решения нашей системы:

При $ \displaystyle _>=-1$, $ \displaystyle _>=1$.

При $ \displaystyle _>=0$, $ \displaystyle _>=2$.

При $ \displaystyle _>=2$, $ \displaystyle _>=10$.

А теперь еще раз посмотри на систему:

Представляешь, что ты решил это за каких-то 15 минут?

Согласись, математика – это все-таки просто, особенно когда, глядя на выражение, не боишься ошибиться, а берешь и решаешь! Ты большой молодец!

Решение неравенств с помощью графиков

Решение линейных неравенств

После последнего примера тебе все по плечу! Сейчас выдохни – по сравнению с предыдущими разделами этот будет очень-очень легким!

Начнем мы, как обычно, с графического решения линейного неравенства. Например, вот этого:

Неравенство нестрогое, поэтому $ \displaystyle 4$ — не включается в промежуток, и решением будут являться все точки, которые находятся правее $ \displaystyle 4$, так как $ \displaystyle 5$ больше $ \displaystyle 4$, $ \displaystyle 6$ больше $ \displaystyle 4$ и так далее:

Ответ: $ x\in \left( 4;+\infty \right)$

Вот и все! Легко? Давай решим простое неравенство с двумя переменными:

Решение неравенства с двумя переменными

\( 2 -3

Такой график у тебя получился? А теперь внимательно смотрим, что там у нас в неравенстве? Меньше? Значит, закрашиваем все, что находится левее нашей прямой.

А если было бы больше Правильно, тогда закрашивали бы все, что находится правее нашей прямой. Все просто.

Решение квадратных неравенств

Теперь будем разбираться с тем, как графически решать квадратные неравенства.

Но прежде, чем перейти непосредственно к делу, давай повторим некоторый материал, касающийся квадратной функции $ \displaystyle a^>+bx+c=0$.

А за что у нас отвечает дискриминант? Правильно, за положение графика относительно оси $ \displaystyle Ox$ (если не помнишь этого, то тогда точно прочти теорию о квадратичных функциях).

В любом случае, вот тебе небольшая табличка-напоминалка:

Теперь, когда мы освежили в памяти весь материал, перейдем к делу – решим графически неравенство \( \displaystyle -^>+10 -21

Симметрично отражаем наши точки на другую ветвь параболы:

А теперь возвращаемся к нашему неравенству \( \displaystyle -^>+10 -21

Ответ: $ \displaystyle x\in \left( -\infty ;3 \right)\cup \left( 7;+\infty \right)$

Долгий способ, правда? Сейчас я покажу тебе более простой вариант графического решения на примере того же неравенства: \( \displaystyle -^>+10 -21

Возвращаемся к нашему неравенству \( \displaystyle -^>+10 -21

Согласись, это намного быстрее.

Запишем теперь ответ: $ \displaystyle x\in \left( -\infty ;3 \right)\cup \left( 7;+\infty \right)$

Рассмотрим еще один способ решения, который упрощает и алгебраическую часть, но главное не запутаться.

Вариант 3

\( \displaystyle -^>+10 -21

Ответ: $ \displaystyle \left[ 2;4 \right]$.

Решение смешанных неравенств

Теперь перейдем к более сложным неравенствам!

\( \displaystyle 4x

У тебя так же? Отлично!

Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть $ \displaystyle _>=^>$.

Смотри, что получилось в итоге:

А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график $ \displaystyle _>=4x$? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!

На каких промежутках по оси $ \displaystyle Ox$ у нас $ \displaystyle _>=^>$ находится выше, чем $ \displaystyle _>=4x$? Верно, $ \displaystyle x\in \left( -2;0 \right)\cup \left( 2;+\infty \right)$.

Это и есть ответ!

Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике

В следующих вебинарах вы сможете отработать навык решения уравнений, неравенств и систем алгебраическим способом.

Решение линейных уравнений (алгебраически)

Цель урока — научиться решать линейные уравнения любого уровня сложности. Линейные уравнения – основа всей алгебры. Научитесь решать линейные уравнения, и вам будет намного проще осваивать всё остальное.

Приёмы, которые мы узнаем на этом уроке, применяются не только в линейных, но во всех типах уравнений, от квадратных до логарифмических. Все приёмы будем разбирать на конкретных примерах и сразу же отрабатывать.

Мы решим разберём все возможные типы линейных уравнений, решив 65 уравнений.

ЕГЭ №15. Решение уравнений и неравенств методом интервалов

В этом видео мы узнаем (вспомним) метод интервалов, поймём как и почему он работает. Вспомним, как решать квадратные, рациональные неравенства, а также неравенства с модулем и иррациональные.

Графическое решение уравнений и неравенств

Уравнением линии на плоскости называют уравнение с двумя переменными или , которому удовлетворяют координаты (абсцисса) и (ордината) любой точки данной линии.

Рассмотрим расположение окружности на координатной плоскости:

1) если уравнение окружности имеет вид +y^=R^" />
, то ее центр находится в точке , а радиус равен (рис. 2.51);

2) если уравнение окружности имеет вид +(y-b)^=R^" />
, то ее центр находится в точке , а радиус равен (рис. 2.52).

Заметим, что неравенству удовлетворяют координаты всех точек плоскости, лежащих внутри окружности +y^= R^" />
, а неравенству удовлетворяют координаты всех точек, лежащих вне этой окружности. Неравенству +y^\leq R^" />
удовлетворяют координаты всех точек плоскости, лежащих внутри окружности +y^= R^" height="" />
и на ее границе.

Рассмотрим расположение квадрата на координатной плоскости:

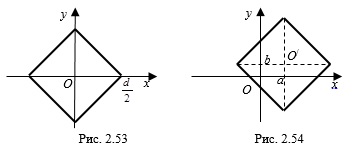
1) если уравнение квадрата имеет вид " />
, то точка – точка пересечения диагоналей квадрата, – длина диагонали квадрата (рис. 2.53);

2) если уравнение квадрата имеет вид " />
, то точка – точка пересечения диагоналей квадрата, – длина диагонали квадрата (рис. 2.54).

Рассмотрим две линии, заданные уравнениями (x;y)=0" />
и (x;y)=0" />
. Чтобы найти точку пересечения этих линий необходимо решить систему уравнений f_(x;y)=0, & \\ f_(x;y)=0.& \end\right." />

1. Рассмотрим уравнение . Это уравнение можно решить графически, если построить в одной системе координат графики функций , и найти их точки пересечения. Абсциссы точек пересечения и будут корнями уравнения .

2. Использование монотонности функций при решении уравнений: если функция строго возрастает, а функция строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем. На рисунке 2.55 число " />
– корень уравнения . Аналогично решаются уравнения, если функция имеет вид (эта прямая параллельна оси абсцисс) (рис. 2.56).

Например, число является единственным корнем уравнения =2x-7" />
, так как левая часть этого уравнения представлена строго убывающей функцией, а правая – строго возрастающей.

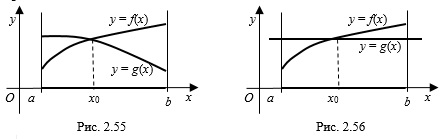
3. Использование монотонности функций при решении неравенств: если функция строго возрастает на некотором отрезке , а функция строго убывает на этом отрезке и " />
– корень уравнения , то решением неравенства является промежуток )" />
, а решением неравенства является промежуток ;b]" />
(рис. 2.57).

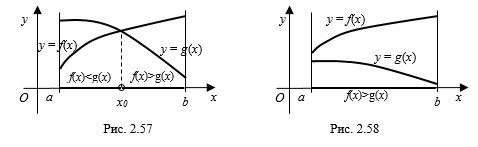
Графики функций на заданном отрезке могут и не пересекаться. Например, на рисунке 2.58 неравенство выполняется на всем отрезке .

Пример 1. Найдите площадь фигуры, ограниченной прямыми , и .

Решение. Построим на координатной плоскости данные прямые (рис. 2.59).

Прямая (1) параллельна оси ординат и проходит через точку . Чтобы построить прямую (2), необходимо знать две точки, принадлежащие этой прямой. Например, можно построить точки , и провести через них прямую (2). Чтобы построить прямую (3), можно построить точки и , принадлежащие этой прямой, и провести через них прямую (3).

Из рисунка 2.59 видим, что треугольник ограничен данными прямыми. Площадь полученного треугольника найдем по формуле ah_" />
, а в нашем случае BC\cdot AD" />
.

1. Найдем координаты точки , решая систему уравнений & \ y=3x, \\ & \ y=x-4. \end" />
Получим точку .

2. Найдем координаты точки , решая систему уравнений & \ x=3, \\ & \ y=3x. \end" />
Получим точку .

3. Найдем координаты точки , решая систему уравнений & \ x=3, \\ & \ y=x-4. \end" />
Получим точку .

Найдем длину отрезка , вычитая из ординаты точки ординату точки . Получим . Найдем длину отрезка , вычитая из абсциссы точки абсциссу точки : . Найдем площадь треугольника : \cdot 10\cdot 5=25" />
.

Ответ: .

$LaTeX formula: \left\<\begin Пример 2. Найдите площадь фигуры, заданной на координатной плоскости системой неравенств x+y\leq 2, & & \\ y-x\leq 2,& & \\ -2\leq y\leq 0.& & \end\right.$

Решение. Построим гранич-ные прямые, соответствующие неравенствам заданной системы: (1), (2), (3), (4) (рис. 2.60). Система неравенств задает на координатной плоскости трапецию , площадь которой найдем по формуле \cdot \left ( DE+AC \right )\cdot OK" />
.

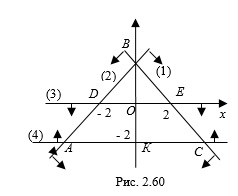
Согласно рисунку 2.60 запишем: , .

Найдем координаты точки , решая систему уравнений & \ y=x+2, \\ & \ y=-2. \end" />
Получим . Аналогично найдем координаты точки . Получим . Тогда .

$LaTeX formula: S=\frac<1> Найдем площадь трапеции: \cdot (4+8)\cdot 2=12$
.

Ответ: .

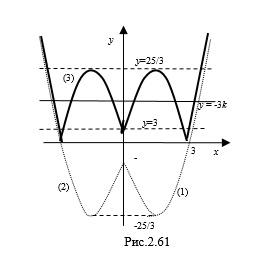
Пример 3. Найдите все целые значений параметра , при которых уравнение -8\left | x \right | -3\right |=-3k" />
имеет шесть корней.

$LaTeX formula: \begin Решение. Заменим данное уравнение равносильной системой уравнений & \ y=\left | 3x^-8\left | x \right | -3\right |, \\ & \ y=-3k. \end$

является парабола, ветви которой направлены вверх. Найдем координаты вершины параболы.

Согласно формулам =-\frac" />
, =f(x_)" />
получим: =\frac" />
, =3\cdot \frac-8\cdot \frac-3=-8\frac" />
. Найдем нули функции (точки пересечения графика с осью абсцисс), решая уравнение -8 x -3=0" />
. Получим =-\frac" />
, =3" />
. Найдем точку пересечения графика с осью ординат: . Построим график (1) (рис. 2.61).

Рассмотрим линейную функцию . Построим семейство прямых, параллельных оси так, чтобы они пересекали график функции -8\left | x \right | -3\right |" />
в шести точках. Это возможно при условии, что или . Очевидно, что промежутку ;-1 \right )" />
принадлежит одно целое значение .

Ответ: .

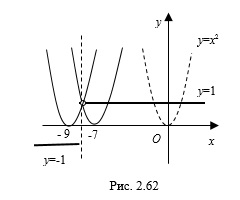
Пример 4. Найдите все значения параметра , при которых уравнение <\left | x+8 \right |>=\left | x+a \right |^" />
имеет один корень.

$LaTeX formula: \left\<\begin Решение. Решим уравнение графически, заменив его равносильной системой уравнений y=\frac<\left | x+8 \right |>, & \\ y=( x+a )^. & \end\right.$

1. Построим схематически график функции <\left | x+8 \right |>" />
(рис. 2.62). Для этого найдем нули функции под знаком модуля: , и раскроем модуль на полученных промежутках, учитывая при этом, что – точка разрыва функции.

1) если , то " />
или ;

2) если , то " />
или .

2. Построим схематически график функции " />
, предварительно построив параболу " />
.

Парабола " />
и прямая имеют две общие точки. Так как согласно условию задачи графики функций <\left | x+8 \right |>" />
и " />
должны иметь только одну точку пересечения, то, выполняя параллельный перенос параболы ." />
на единичных отрезка влево, заметим, что при парабола " />
и прямая имеют одну точку пересечения, а при уже не имеют общих точек. Следовательно, если принимает значения из промежутка , то графики функций <\left | x+8 \right |>" />
и " />
имеют одну общую точку, а уравнение <\left | x+8 \right |>=\left | x+a \right |^" />
имеет одно решение.

Ответ: .

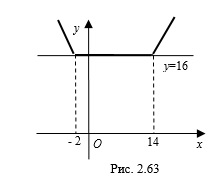
Пример 5. Найдите все значения параметра , при которых уравнение " height="" />
имеет бесконечно много решений.

$LaTeX formula: \begin Решение. Решим уравнение графически, заменив его равносильной системой уравнений & \ y=| x -14\right |+\left | x+2 \right |, \\ & \ y=-a^. \end$

1. Построим схематически график функции . Для этого найдем нули функций, записанных под знаками модулей, решая уравнения , откуда и , откуда . Раскроем модули на полученных промежутках и построим графики функций на этих промежутках (рис. 2.632):

1) если , то или ;

2) если , то или ;

3) если , то или .

Построим прямую " />
так, чтобы она имела с графиком функции бесконечно много общих точек. Очевидно, что это возможно в том случае, если =16" />
, откуда " />
.

$LaTeX formula: a=-2\sqrt[3]<2> Ответ:$
.

Пример 6. Найдите все значения параметра , при которых система уравнений & \ \left | x \right |+\left | y \right |=8, \\ & \ x^+y^=4a \end" height="" />
имеет четыре решения.

Решение. Имеем уравнение квадрата и уравнение окружности +y^=4a" height="" />
.

1. Построим квадрат с центром в точке и диагональю (рис. 2.64).

Площадь квадрата найдем по формуле d^" height="" />
. Получим: 16^" height="" />
. С другой стороны площадь квадрата можно вычислить по формуле " height="" />
, где – сторона квадрата. Тогда =128" height="" />
и " height="" />
.

2. Построим окружность с центром в точке и радиусом (рис. 2.64). Поскольку система уравнений & \ \left | x \right |+\left | y \right |=8, \\ & \ x^+y^=4a \end" height="" />
имеет четыре решения, то окружность должна быть вписана в квадрат, тогда ее радиус " height="" />
или >" height="" />
, откуда или описана около квадрата, тогда радиус окружности " height="" />
или , откуда .

Ответ: ; .

$LaTeX formula: \left | x-7 \right |+\left | y-2 \right |\leq 10$

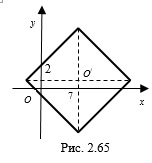
Пример 7. Найдите площадь и периметр фигуры, заданной неравенством .

$LaTeX formula: \left | x-7 \right |+\left | y-2 \right |= 10$

Решение. Данному неравенству удовлетворяют координаты всех точек плоскости, расположенных внутри квадрата и на его границе.

Построим квадрат с центром в точке " height="" />
и диагональю (рис. 2.65). Найдем площадь квадрата. Согласно формуле d^" height="" />
получим \cdot 20^=200" height="" />
.

С другой стороны площадь квадрата находят по формуле " height="" />
, где – сторона квадрата.

Тогда =200" height="" />
, " height="" />
. Найдем периметр квадрата: " height="" />
.

Ответ: , " height="" />
.

Решая уравнение или систему уравнений графически, точное решение найти бывает достаточно сложно, а то и вовсе не возможно. Поэтому этот метод чаще всего применяют в случае, когда необходимо определить количество корней уравнения или найти их приближенное значение.

Читайте также: