Двойной интеграл в декартовых координатах конспект
Обновлено: 04.07.2024
Для дальнейшего предположим, что область D имеет такое устройство: она ограничена графиками функций и и прямыми x = a и x = b (рис. 1.7). Каждая прямая, параллельная оси Оy (кроме прямы x = a и x = b) (рис. 1.8.) пересекает границу области D в двух точках. Нижнюю из этих точек будем называть точкой входа, а верхнюю – точкой выхода. Если D имеет другую конструкцию, то её разбивают и сводят к конструкции области D и далее используют свойство аддитивности интеграла.
Чтобы вычислить (1.48) интерпретируем его как массу М пластинки D. Найдем массу этой же пластинки иначе.
Рассмотрим узкий вертикальный стержень между прямыми х и x + dx (рис. 1.7) оси Ох.
(dx – постоянно). (1.49)
Так как эта же масса выражается двойным интегралом (1/36), то
Методическое руководство
Чтобы вычислить двойной интеграл, надо проинтегрировать f(x,y) по у, считая х – фиксированным, в пределах от точки входа до точки выхода, а затем полученный результат проинтегрировать по х в пределах его наибольшего изменения.
Следовательно, для вычисления двойного интеграла нужно произвести последовательное вычисление двух обычных определенных интегралов. Интеграл
вычисляется первым, называется внутренним, а интеграл
называется внешним.
Если область D такая, как показано на рис.

1.9, то внутренне интегрирование удобно вести по х. Получается операция, которая носит название: изменения порядка интегрирования
Формула (1.52) доказывается точно так же как и (1.51). Поскольку речь идет о массе одной и той же пластинки D, то
Методическое руководство
На практике трудность вычисления двойного интеграла обычно состоит в расстановке пределов. Следует руководствоваться следующей последовательностью действий:
1) сделать схематический рисунок области D, записав уравнения линий;
2) выбрать вполне определенный порядок интегрирования;
3) найти пределы для внешнего интеграла и расставить их;
5) приступить к расстановке пределов для внутреннего интеграла: точка входа всегда лежит на кривой с определенным уравнением, с момента которой изменяется переменная интегрирования для внутреннего интеграла, точка выхода – на кривой, на которой заканчивается её изменение в области D, поэтому нижним пределом будет значение функции, на которой лежит точка входа; верхним – значение функции на которой лежит точка выхода.
Пример 1
Найти , где D: .
Решение: Используя методическое руководство, выберем определенный порядок интегрирования и расставим пределы интегрирования:
Пример 2
Найти площадь, ограниченную параболами y = x 2 и (рис. 1.10).
Решение. По свойству (1.44)
Для расстановки пределов необходимо решить систему:
Отсюда: x1 = 0; х2 = 1, тогда
Пример 3
Изменить порядок интегрирования:
Решение. Рекомендуется по заданным пределам во внешнем и внутреннем интегралах воспроизвести область интегрирования D: x = 0 и x = 1; y =x 2 и y = x (рис. 1.11).
Пример 4
Вычислить объем тела, ограниченного поверхностями: z = x 2 + y 2 , x = 0, x = 1 ; y = 0, y = (рис. 1.12).
Решение. Воспользуемся формулой (1.41):
Пример 5
Вычислить , D – треугольник с вершинами О(0,0), A(2,0) и B(2,1) (рис. 1.13).
Решение. Область D ограничена прямыми y = 0, , x =2. Тогда
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Материал представлен на сайте исключительно в ознакомительных целях.
Все права принадлежат авторам этих материалов.
Вычисление двойного интеграла сводится к вычислению двух определенных интегралов следующим способом.
Пусть область G (рис. 6.3) ограничена кривыми
причем всюду на отрезке функции и непрерывны и . Тогда
причем сначала вычисляется внутренний определенный интеграл по переменной y, а полученный результат интегрируется во внешнем определенном интеграле по переменной x. При этом интеграл, стоящий в правой части формулы, называют повторным или двукратным интегралом.
Аналогично, если область G (рис. 6.3) ограничена кривыми
причем всюду на отрезке функции и непрерывны и , то
причем сначала вычисляется внутренний определенный интеграл по переменной x, а полученный результат интегрируется во внешнем определенном интеграле по переменной y.
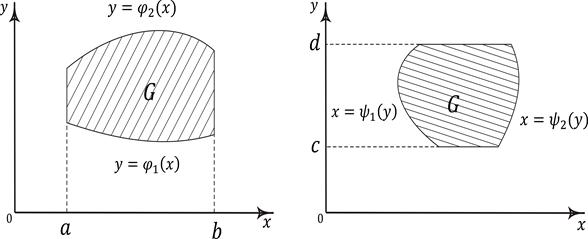
Рис. 6.3. Вычисление двойного интеграла в декартовых координатах
Пример. Вычислить двойной интеграл
если область интегрирования G ограничена линиями .
Форма области G (рис. 6.4) позволяет применить первую формулу при :
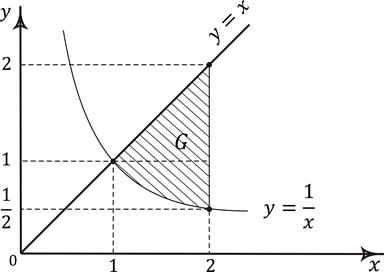
Рис. 6.4. Пример вычисления двойного интеграла в декартовых координатах
Если же для вычисления данного двойного интеграла применить вторую формулу, то следует положить
Тогда, используя свойство 3 двойного интеграла, получим:
Очевидно, что в данном примере целесообразнее проводить вычисления по первой формуле.
Вычисление двойного интеграла как предела интегральной суммы, так же как и в случае определенного интеграла, связано обычно с большими трудностями. Чтобы их избежать, вычисление двойного интеграла сводят к последовательному вычислению двух определенных интегралов. Покажем, как это делается. Для простоты при выводе ограничимся случаем, когда в области интегрирования а подынтегральная функция . Такое предположение позволяет нам рассматривать двойной интеграл как объем цилиндрического тела.
Итак, требуется вычислить двойной интеграл от непрерывной функции .
Предположим сперва, что область интегрирования а ограничена двумя непрерывными кривыми и двумя прямыми причем для всех значений заключенных между а и имеет место неравенство (рис. 231).
Проведем через точку оси прямую, параллельную Эта прямая встречает кривые, ограничивающие область а, соответственно в точках Точку будем называть точкой входа, а точку — точкой выхода. Их ординаты обозначим соответственно и увых. Ордината точки входа равна а ордината точки выхода равна Известно, что двойной интеграл численно равен объему V цилиндрического тела, ограниченного частью поверхности , которая проектируется в площадку а (см. рис. 227):
Подсчитаем теперь объем У цилиндрического тела иначе, а именно, с помощью метода поперечных сечений (см. гл. VIII, § 3, п. 3).
Как мы знаем, если сечение тела плоскостью, перпендикулярной к оси Ох, проходящей через точку с абсциссой имеет площадь , то объем V тела выражается формулой
Применим эту формулу к вычислению объема цилиндрического тела. Проведя через точку плоскость, перпендикулярную оси мы получим в сечении криволинейную трапецию (рис. 232). Аппликата точек линии МХМ при постоянном является функцией только от причем у изменяется в границах от до увых Площадь трапеции очевидно, равна определенному интегралу:
Итак, формула (7) выражает площадь поперечного сечения цилиндрического тела.
Подставляя в формулу (6) выражение для получим
Но так как, с другой стороны, объем V цилиндрического тела равен двойному интегралу то имеем
Эта и есть искомая формула.
Поясним смысл формулы (I). Для того чтобы вычислить двойной интеграл нужно сперва вычислить определенный интеграл считая постоянным (или, как говорят, вычислить внутренний интеграл).
Нижней границей интегрирования является ордината точки входа а верхней границей интегрирования является ордината точки выхода увых соответствующие данному фиксированному значению Результат вычисления этого интеграла является функцией только от Интегрируя теперь эту функцию в границах от а до b, получим значение двойного интеграла. Сделаем следующие замечания.
Если область о ограничена двумя кривыми двумя горизонтальными прямыми причем для всех у между (рис 233), то аналогично можно доказать, что имеет место равенство
Здесь при внутреннем интегрировании у следует считать постоянным. Результат этого интегрирования будет функцией от у, которую затем следует проинтегрировать в границах от с до d.
Интегралы, стоящие в правых частях формул (I) и (II), называют повторными или двукратными интегралами.
Замечание 2. Следует обратить внимание на то, что в формулах (I) и (II) границы внешнего интеграла всегда постоянны.
Замечание 3. Формулы (I) и (II) выведены в предположении, что область а имеет специальный вид. Если контур области а более сложный (рис. 234), то поступают так: область разбивают на конечное число частей, удовлетворяющих условиям, при которых была выведена формула (I) или (II). Затем вычисляют интеграл по формуле (I) или (II) для каждой из таких областей. Интеграл же по всей области, в силу свойства аддитивности, равен сумме интегралов по каждой из этих частей. Для случая, приведенного на рис. 234, имеем:
Если областью интегрирования а служит прямоугольник, ограниченный прямыми (рис. 235), то формулы (I) и (II) для этого случая примут вид:
Рассмотрим примеры на вычисление двойных интегралов. Пример 1. Вычислить двойной интеграл если областью интегрирования а является треугольник, ограниченный прямыми (рис. 236).
Решение. Если при вычислении двойного интеграла пользоваться формулой (I), то здесь как точки входа лежат на оси Ох, а точки выхода — на прямой
Поэтому, применяя формулу (I), имеем
Вычислим внутренний интеграл, в котором считаем постоянным:
Применяя для вычисления двойного интеграла формулу (II), получим, конечно, тот же результат. Замечая, что в этом случае (так как точка входа лежит на прямой или , а точка выхода на прямой (см. рис. 236), получим
Если принять во внимание геометрический смысл двойного интеграла, то дает объем V цилиндрического тела, ограниченного сверху частью параболоида вращения которая проектируется на плоскость в треугольник .
Пример 2. Вычислить двойной интеграл если область интегрирсвания а ограничена линиями (рис. 237).
Решение. Применим для вычисления двойного интеграла формулу (I). Здесь . Поэтому
Вычислим внутренний интеграл, в котором считаем я постоянным:
Если при вычислении двойного интеграла пользоваться формулой (II), то придется область интегрирования а разбить на две части и (см. рис. 237), так как линия ОАВ, на которой расположены точки выхода на отдельных участках, задается различными уравнениями. По свойству аддитивности
Применяем формулу (II) к каждому из интегралов, стоящих в правой части последнего равенства:
так как Вычисляем внутренний интеграл, помня, что у — постоянно:
Таким образом, окончательно,
Этот пример показывает, что для нахождения двойного интеграла в данном конкретном случае выгоднее применить формулу (I). Это следует иметь в виду при вычислении двойных интегралов и пользоваться той из формул (I) или (II), применение которой ведет к менее громоздким вычислениям.
1) область первого вида, т. е. область, ограниченную слева и справа прямымиСоответственно, снизу - кривой, сверху — кривой, каждая из которых пересекается с вертикальюТолько в одной точке (рис. 19.3);
2) область второго вида, т. е. область, ограниченную снизу и сверху прямымиСоответственно, слева — кривойСправа
- кривойКаждая из которых пересекается с горизонтальюТолько в одной точке (рис. 19.4).
Замечание. В некоторых случаях точкиИ,И,И,
ИМогут сливаться в одну.
Если для функцииОпределенной в области, существует двойной
Интеграл, а при каждом постоянном значенииИзПростой интеграл


То существует также н повторный интеграл . и выполняется равенство

= | /(*, У) -) сК = |йх | /(*, у) Оу, (19.5)
Если функцияИнтегрируемая в прямоугольнике, может

Быть представлена в виде произведения функции только от дс на функцию только от>>:То



Пример 19.2. Вычислить, где областьЯвляется
Прямоугольником [4,8; 1,2].
Задача сводится к вычислению повторного интеграла с помощью формулы (19.5). По этой формуле интегрирование выполняется сначала по, в пределах отДо при произвольном постоянномJ а потом поУ в пределах отДо Формула (19.5) в данном случае принимает вид




Замечание. Тот же результат можно получить и по формуле (19.6).

| Оу |хуйх = 124^ = 12>-2|* = 12 (4 -1) = 36.
Пример 19.3. Вычислить ДОхгуДхс1у, 8 - область, ограниченная



Ниями у = - х2, х = у2.
Данные линии пересекаются в двух точках 0(0,0), М(1,-1) (рис. 19.6). Область 5 можно рассматривать как область первого вида 5] и как область второго вида &2-Рассматривая ее как область первого вида, получаем следующие пределы интегрирования а = 0, Ь = \,у = ф,(лг) = -->/х, у = (р2(х) = - х2. По формуле (19.3) имеем
^х2ус! хс1у = ^сЬс ^x2у(^у.







Следовательно, ДО х2ус1хс1у = -

Замечание. Рассматривая данную область как область второго вида, находим следующие пределы интегрирования: с =—1, с/ = 0, х = у,(.у) = .у2,
Читайте также:

