Балочные системы техническая механика конспект
Обновлено: 30.06.2024
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).

q — интенсивность нагрузки; I — длина стержня;
G = ql — равнодействующая распределенной нагрузки.
Разновидности опор балочных систем (см. лекцию 1)
Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с длиной.
Жесткая заделка (защемление) (рис. 6.2)

Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы Rax и и парой с моментом Mr.
Для определения этих неизвестных удобно использовать систему уравнений в виде

Каждое уравнение имеет одну неизвестную величину и решается без подстановок.
Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например
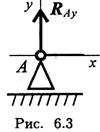

Шарнирно-подвижная опора (рис. 6.3)
Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
Балка на двух шарнирных опорах (рис. 6.5)
 |
Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:

Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.

Для контроля правильности решения используется дополнительное уравнение

При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):

Примеры решения задач
Пример 1. Одноопорная (защемленная) балка нагружена сосредоточенными силами и парой сил (рис. 6.7). Определить реакции заделки.
 |
Решение
2. В заделке может возникнуть реакция, представляемая двум: составляющими (RAy,RAx), и реактивный момент МA. Наносим на схему балки возможные направления реакций.
В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.
3. Используем систему уравнений:

Знаки полученных реакций (+), следовательно, направления реакций выбраны верно.
3. Для проверки правильности решения составляем уравнение моментов относительно точки В.

Подставляем значения полученных реакций:

Решение выполнено верно.
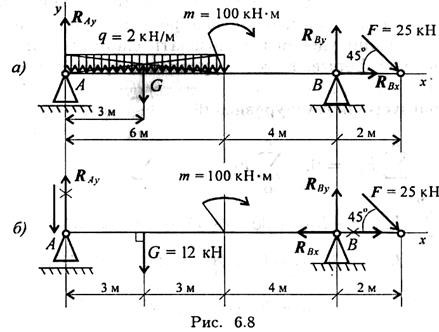
Пример 2. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 6.8а). Определить реакции опор.
 |
Решение
1. Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.
Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.
2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецелесообразно.
3. Заменяем распределенную нагрузку сосредоточенной:
G = ql; G = 2*6 = 12 кН.
Сосредоточенную силу помещаем в середине пролета, далее задача решается с сосредоточенными силами (рис. 6.8, б).
4. Наносим возможные реакции в опорах (направление произвольное).
5. Для решения выбираем уравнение равновесия в виде

6. Составляем уравнения моментов относительно точек крепления:

7. Используя уравнение проекций, получим:

RBx — горизонтальная реакция в опоре В.
Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному.
8. Проверка правильности решения. Для этого используем четвертое уравнение равновесия


Подставим полученные значения реакций. Если условие выполнено, решение верно:
-5,1 - 12 + 34,6 – 25 -0,7 = 0.
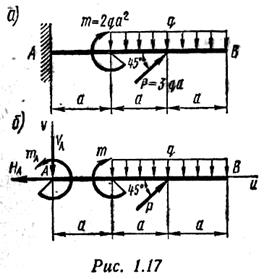
Пример 3. Определить опорные реакции балки, показанной на рис. 1.17, а.
Решение
Рассмотрим равновесие балки АВ. Отбросим опорное закрепление (заделку) и заменим его действие реакциями НА,VA и тА (рис. 1.17, б). Получили плоскую систему произвольно расположенных сил.
Выбираем систему координат (рис. 1.17,6) и составляем уравнения равновесия:

Составим проверочное уравнение

следовательно, реакции определены верно.

Пример 4. Для заданной балки (рис. 1.18, а) определить опорные реакции.
Решение
Рассматриваем равновесие балки АВ. Отбрасываем опорные закрепления и заменяем их действие реакциями (рис. 1.18,6). Получили плоскую систему произвольно расположенных сил.

Выбираем систему координат (см. рис. 1.18,6) и составляем уравнения равновесия:

равнодействующая равномерно распределенной нагрузки интенсивностью q1,

расстояние от точки А до линии действия равнодействующей q1(а + b);

равнодействующая равномерно распределенной нагрузки интенсивностью q2;

расстояние от точки А до линии действия равнодействующей q2 (d — с).
Подставив числовые значения, получим

откуда VB = 28,8 кН;


— расстояние от точки В до линии действия равнодействующей q1 (a+b);

— расстояние от точки В до линии действия равнодействующей q2(d — c).
Подставив числовые значения, получим:

откуда VA = 81,2 кН.
Составляем проверочное уравнение:
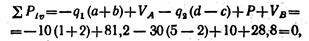
следовательно, опорные реакции определены верно.
Пример 5. Для заданной стержневой системы (рис. 1.19, а) определить усилия в стержнях.

Решение
Рассмотрим равновесие балки AB, к которой приложены как заданные, так и искомые силы.
На балку действуют равномерно распределенная нагрузка интенсивностью q, сила Р и сосредоточенный момент т.
Освободим балку от связей и заменим их действие реакциями (рис. 1.19, б). Получили плоскую систему произвольно расположенных сил.
Выбираем систему координат (см. рис. 1.19, б) и составляем уравнения равновесия:

где q (a + b) — равнодействующая
равномерно распределенной нагрузки интенсивностью q (на чертеже она показана штриховой линией).
Подставив числовые значения, получим:

откуда NAC = 16 кН;

Напомним, что сумма проекций сил, образующих пару, на любую ось равна нулю;

где NBD cos α — вертикальная составляющая силы NBD', NBFcos β — вертикальная составляющая силы NBF(линии действия горизонтальных составляющих сил NBDи NBF проходят через точку А и поэтому их моменты относительно точки А равны нулю). Подставляя числовые значения и учитывая, что NBD= 1,41 NBF, получаем:

откуда NBF = 33,1 кН.
Тогда NBD = 1,41*33,1 = 46,7 кН.
Для определения усилий в стержнях не было использовано уравнение равновесия: ΣPto= 0. Если усилия в стержнях определены верно, то сумма проекций на ось v всех сил, действующих на балку, должна быть равна нулю. Проектируя все силы на ось v, получаем:

следовательно, усилия в стержнях определены верно.
Пример 6. Для заданной плоской рамы (рис. 1.20, а) определить опорные реакции

Решение
Освобождаем раму от связей и заменяем их действие реакциями NА, VA, VB (рис. 1.20, б). Получили плоскую систему произвольно расположенных сил.

Выбираем систему координат (см. рис. 1.20, б) и составляем уравнения равновесия:
где Р2 cos α — вертикальная составляющая силы Р2;
P2 sin α — горизонтальная составляющая силы Р2;
2qa — равнодействующая равномерно распределенной нагрузки интенсивностью q (показана штриховой линией);

откуда VB = 5,27qa;



линия действия силы Р2 cosα проходит через точку В и поэтому ее момент относительно точки В равен нулю

откуда VA = 7qa.
Для определения реакций не было использовано уравнение равновесия ΣPiv=0. Если реакции определены верно, то сумма проекций на ось v всех сил, действующих на раму, должна быть равна нулю. Проектируя все силы на ось v, получаем:

следовательно, опорные реакции определены верно.
Напомним, что сумма проекций сил, составляющих пару с моментом т, на любую ось равна нулю.
Контрольные вопросы и задания
1. Замените распределенную нагрузку сосредоточенной и определите расстояние от точки приложения равнодействующей до опоры А (рис. 6.9).

2. Рассчитайте величину суммарного момента сил системы относительно точки А (рис. 6.10).

3. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в заделке?
4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?
 |
5. Определите реактивный момент в заделке одноопорной балки, изображенной на схеме (рис. 6.11).
6. Определите вертикальную реакцию в заделке для балки, представленной на рис. 6.11.
Балка – это конструктивная деталь в виде прямого бруса, закрепленного на опорах, и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с ее длиной. Балки используются в строительстве, машиностроений, авиаций и кораблестроений.
Балки являются основными элементами конструкций и по этому, расчет балки являются важной и ответственной задачей.
Балка называется статически определимой, если число опорных реакции в балке, не превышает числа уравнений равновесия системы.
Виды статически определимых балок:

Часто встречаются следующие поперечные сечения балок:

Виды нагрузок.По способу приложения нагрузки делятся на сосредоточенные, и распределенные. Если передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузка называется сосредоточенной.
Если нагрузка распределена по значительной площадке или линии (давление воды на плотину, снега на крышу и т. д.), то она является распределенной. При расчете распределенную нагрузку приводим в сосредоточенную нагрузку, по формуле , здесь интенсивность распределенной нагрузки, длина распределенной нагрузки. Полученная сосредоточенная сила должна быть приложена в центре распределенной нагрузки.

При воздействии нагрузок на балку, со стороны крепления (жесткая заделка, шарнирно подвижная и неподвижная опора) на балку действует силы реакций, для того чтобы рассчитать балку на изгиб, надо определить эти опорные реакций.
Алгоритм определения опорных реакций статически определимых балок:
1. Отбрасываем связи и заменяем их реакциями.
2. В случае действия распределенной нагрузки приводим в сосредоточенную нагрузку.
3. Если есть сосредоточенные и распределенные нагрузки, оставляем нагрузки в точке их действия.
4. Принимает оси координат.
5. Составляем уравнения равновесия:
; 2) 0; 3) .
6. Решаем составленные уравнения, и определяем опорные реакций.
1. Что такое балка, где они используются?
2. Перечислите поперечные сечения балок…
3. Что такое статически определимая балка?
4. Какие виды нагрузок знаете?
5. Какой буквой обозначается интенсивность распределенной нагрузки, и
укажите единицу измерения интенсивности распределенной нагрузки?
6. По какой формуле распределенная нагрузка приводиться в сосредоточенную нагрузку?
7. Где нужно приложить приведенную сосредоточенную силу?
8. Алгоритм определения статически определимой балки:
Пример 2.1.
Определить реакции опор балки (рис. 22.).


1. Отбрасываем связи и заменяем их реакциями (рис. 23б.).
2. В случае действия распределенной нагрузки приводим в сосредоточенную нагрузку (рис. 23б.).
3. Если есть сосредоточенные и распределенные нагрузки, оставляем нагрузки в точке их действия.
4. Принимает оси координат.
5. Составляем уравнения равновесия:

6. Сумма проекции сил относительно оси должна равняться нулю:
7. ;

Сумма проекции сил относительно оси должна равняться нулю:
2) 0;
От второго уравнения не сможем определить или .

Составляем, трете уравнение, сумма моментов относительно точки должна равняться нулю:
отсюда определяем .



По условию равновесия сумма моментов относительно любой точки должна равняться нулю, по этому, составляем уравнение равновесие относительно точки . То есть, сумма моментов относительно точки тоже должна равняться нулю.
4) отсюда определяем


Таким образом, мы определили опорные реакции и , для проверки результатов можем, воспольвоваться вторым уравнением:




Есть равновесия относительно оси , значить мы правильно определили опорные реакции.
Ответ: и .
Пример 2.2.
Определить реакции опор балки (рис. 24.).


1. Отбрасываем связи и заменяем их реакциями (рис. 25б.).
2. В случае действия распределенной нагрузки приводим в сосредоточенную нагрузку (рис. 25б.).
3. Если есть сосредоточенные и распределенные нагрузки, оставляем нагрузки в точке их действия.
4. Принимает оси координат.
5. Составляем уравнения равновесия:


Сумма проекции сил относительно оси должна равняться нулю:
; _______________

Сумма проекции сил относительно оси должна равняться нулю:
2) 0;

От второго уравнения не сможем определить или .

Составляем, трете уравнение, сумма моментов относительно точки должна равняться нулю:

_____

По условию равновесия сумма моментов относительно любой точки должна равняться нулю, по этому, составляем уравнение равновесие относительно точки . То есть, сумма моментов относительно точки тоже должна равняться нулю.

4) _______

.
Таким образом, мы определяем опорные реакции и , для проверки результатов можем, воспольвоваться вторым уравнением:

_____



С двух сторон равенства должна получиться одинаковые числа, тогда будет равновесия относительно оси . Если вышли одинаковые числа, значить мы можем считать что, правильно определили опорные реакции. Если не выходят, значить вы допустили ошибку!
Ответ: и .
Для решения второй задачи контрольной работы 1 (задачи 11-20) следует выполнить следующие действия:
1) Изучить темы 3,4,5.
2) Ответить на контрольные вопросы по темам 3,4,5.
2) Выполнить самостоятельно пример 2.2.
Схему и данные своего варианта для второй задачи контрольной работы 1 возьмете с рисунка 26.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).
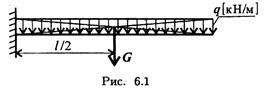
q — интенсивность нагрузки; I — длина стержня;
G = ql — равнодействующая распределенной нагрузки.
Разновидности опор балочных систем (см. лекцию 1)
Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с длиной.
Жесткая заделка (защемление) (рис. 6.2)
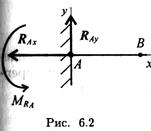
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы Rax и и парой с моментом Mr.
Для определения этих неизвестных удобно использовать систему уравнений в виде
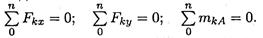
Каждое уравнение имеет одну неизвестную величину и решается без подстановок.
Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например
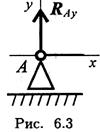
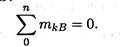
Шарнирно-подвижная опора (рис. 6.3)
Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
Балка на двух шарнирных опорах (рис. 6.5)
 |
Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:

Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.
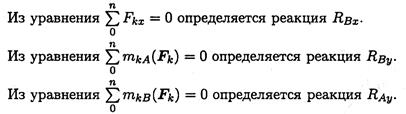
Для контроля правильности решения используется дополнительное уравнение
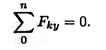
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):
Технический портал, посвященный Сопромату и истории его создания
В машинах и сооружениях очень часто встречаются тела удлиненной формы, называемые балками (или балочными системами). Балки в основном предназначены для восприятия поперечных нагрузок. Балочные системы имеют специальные опорные устройства для сопряжения их с другими элементами и передачи на них усилий.
Различают следующие типы опор.
Шарнирно-подвижная опора (рис.а).

Шарнирно- подвижная опора
Такая опора допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. В этой опоре известны точка приложения опорной реакции — центр шарнира и ее направление — нормаль к опорной поверхности (трением катков пренебрегают).
Таким образом, здесь остается одна неизвестная — опорная реакция RА.
Схематические изображения шарнирно подвижных опор приведены на рис. б—г. Следует отметить, что опорная поверхность шарнирно подвижной опоры может быть непараллельна оси балки (рис. г). Реакция RА в этом случае не будет перпендикулярна оси балки, так как она перпендикулярна опорной поверхности.
Шарнирно-неподвижная опора (рис. а).
Эта опора допускает поворот вокруг оси шарнира, но не допускает никаких линейных перемещений. В данном случае известна только точка приложения опорной реакции — центр шарнира; направление и величина опорной реакции неизвестны. Обычно вместо определения величины и направления реакции (полной) находят ее горизонтальную и вертикальную составляющие VА и HА.
Схематические изображения шарнирно-неподвижных опор приведены на рис. б-г.
Жесткая заделка (защемление)

Жесткая заделка (защемление)
Такая опора не допускает ни линейных перемещений, ни поворота.
Неизвестными в данном случае являются не только величина и направление реакции, но и точка ее приложения. Таким образом, для определения опорной реакции следует найти три неизвестных: составляющие VА и HА опорной реакции по осям координат и реактивный момент mА относительно центра тяжести опорного сечения.
Опорные реакции можно также обозначать буквами, соответствующими координатным осям, вдоль которых онн направлены, с индексом, отвечающим опоре. Например, YА и XА или просто буквами А и В и т. п.
Читайте также:

