Отрицание высказывательных форм кратко
Обновлено: 02.07.2024
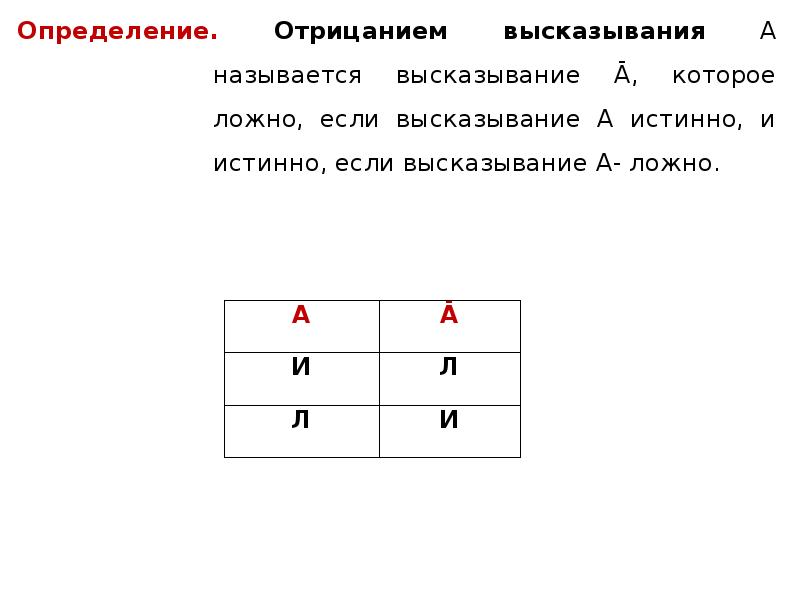
Определение. Отрицанием высказывания А называется высказывание Ā, которое ложно, когда высказывание А истинно, и истинно, когда высказывание А – ложно.
Таблица истинности отрицания имеет вид :
| А | Ā |
| и | л |
| л | и |
Из данного определения следует, что предложение и его отрицание не могут быть ни одновременно истинны, ни одновременно ложны.
Построим отрицание ложного высказывания «число 28 делится на 9:
А) Число 28 не делится на 9.
Б) Неверно, что число 28 делится на 9.
Высказывания, которые мы получили, истинные. Значит, отрицание данного предложения построено правильно.
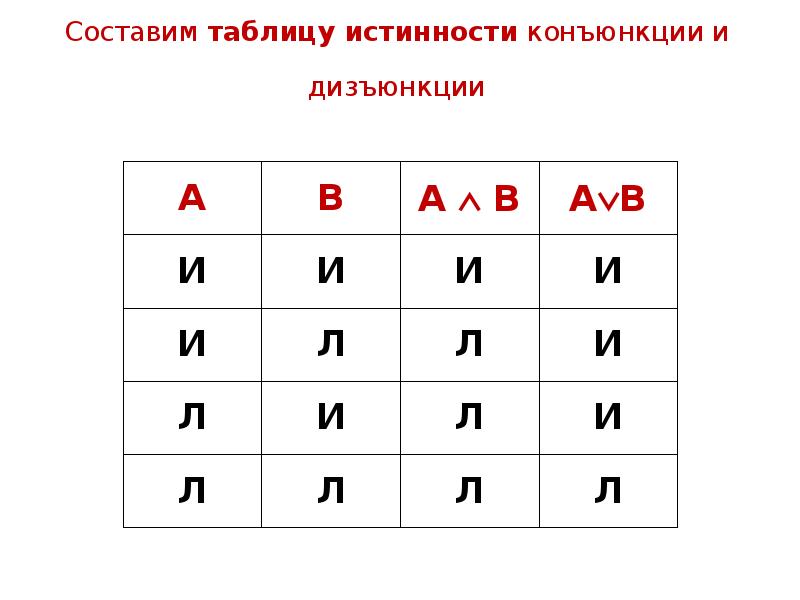
Можно доказать, что отрицанием конъюнкции двух высказываний А и В является дизъюнкция их отрицаний. Для этого надо убедиться в том, что значения истинности высказываний вида А∧В и А∨ В совпадают при любых значениях истинности высказываний А и В. Сделать это можно при помощи таблицы истинности:
| А | В | А∧В | А∧В | А | В | А∨ В |
| и | и | и | л | л | л | л |
| и | л | л | и | л | и | и |
| л | и | л | и | и | л | и |
| л | л | л | и | и | и | и |
Про высказывания вида А∧В и А∨ В говорят, что они равносильны, и пишут
Аналогично можно доказать, что имеет место равносильность
Эти равносильности носят название законов де Моргана.
10. Отношения следования и равносильности между предложениями.
Определение.Высказывательная форма В(х) следует из высказывательной формы А (х), если В(х) обращается в истинное высказывание при всех тех значениях х, при которых А (х) истинна.
Если А и В - высказывания, тогда говорят, что из А следует В, если всякий раз, когда А истинно, истинно и В.
Для обозначения отношения логического следования используется знак Þ. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) Þ В(х), прочитать которое можно по - разному:
1. Из А(х) следует В(х).
2. Всякое А(х) есть В(х).
3. Если А(х), то В(х).
4. В(х) есть следствие А(х).
5. А(х) есть достаточное условие для В(х).
6. В(х) есть необходимое условие для А(х).
- Всякое число, которое кратно 4, кратно и 2.
- Если число кратно 4, то оно кратно и 2.
- Кратность числа 2 есть следствие кратности его 4.
- Кратность числа 4 есть достаточное условие для его кратности 2.
- Кратность числа 2 есть необходимое условие для его кратности 4.
Определение. Предложения А(х) и В(х) равносильны, если из предложения А(х) следует предложение В(х), а из предложения В(х) следует предложение А (х).
Для обозначения отношения равносильности используется знак Û. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) Û В(х), прочитать которое можно по-разному:
1. А(х) равносильно В(х).
2. А(х) тогда и только тогда, когда В(х).
3. А(х) - необходимое и достаточное условие для В(х).
4. В(х) - необходимое и достаточное условие для А(х).
· Число делится на 3 тогда и только тогда, когда сумма цифр вегозаписи делится на 3.
· Для того чтобы число делилось на 3, необходимо и достаточно, чтобы сумма цифр в его записи делилась на 3.
Высказывательные формы (предикаты), так же как и высказывания, бывают элементарными и составными. Составные высказывательные формы образуются из элементарных при помощи тех же логических связок, которые используются в составных высказываниях.
Пусть на множестве Х задана высказывательная форма А(х).
Отрицанием высказывательной формы (предиката) А(х), заданной на множестве Х, называется высказывательная форма Ā(х), заданная на том же множестве, которая истинна при тех значениях хÎХ, при которых данная форма А(х) ложна, и, наоборот, ложна при тех значениях хÎХ, при которых данная форма А(х) истинна.
Таким образом, сформулируем правило нахождения множества истинности отрицания высказывательной формы Ā(х), если известно множество истинности данной формы А(х).
Если ТА - множество истинности высказывательной формы А(х), хÎХ, то множеством истинности ТĀ - высказывательной формы Ā(x), хÎX, является дополнение к множеству ТА до области определения Х, т.е.
Этот вывод дает возможность находить множество истинности отрицания высказывательной формы по множеству истинности данной высказывательной формы.
Например, дана форма А(х): «х
Таким образом, для построения отрицания высказывания с кванторами нужно:
1) квантор общности заменить на квантор существования или, наоборот, квантор существования заменить на квантор общности;
2) для высказывательной формы (предиката) сформулировать отрицание.
В символах это правило можно записать:
= ( х ÎХ) Ā(х);
= ( х ÎХ) Ā(х).
1. Дано высказывание: ( xÎZ)(x+5=8), оно истинно. Образуем его отрицание: ( xÎZ)(х+5≠8) – это высказывание ложно.

2. Для ложного высказывания ( xÎR) (х
Высказывательные формы (предикаты), так же как и высказывания, бывают элементарными и составными. Составные высказывательные формы образуются из элементарных при помощи тех же логических связок, которые используются в составных высказываниях.
Пусть на множестве Х задана высказывательная форма А(х).
Отрицанием высказывательной формы (предиката) А(х), заданной на множестве Х, называется высказывательная форма Ā(х), заданная на том же множестве, которая истинна при тех значениях хÎХ, при которых данная форма А(х) ложна, и, наоборот, ложна при тех значениях хÎХ, при которых данная форма А(х) истинна.
Таким образом, сформулируем правило нахождения множества истинности отрицания высказывательной формы Ā(х), если известно множество истинности данной формы А(х).
Если ТА - множество истинности высказывательной формы А(х), хÎХ, то множеством истинности ТĀ - высказывательной формы Ā(x), хÎX, является дополнение к множеству ТА до области определения Х, т.е.
Этот вывод дает возможность находить множество истинности отрицания высказывательной формы по множеству истинности данной высказывательной формы.
Вы можете изучить и скачать доклад-презентацию на тему Высказывания. Отрицание высказываний. Пример и контрпример. Основные логические. Презентация на заданную тему содержит 32 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!



























Высказывания. Отрицание высказываний. Пример и контрпример. Основные логические операции. Высказывания. Отрицание высказываний. Пример и контрпример. Основные логические операции. План Высказывания и высказывательные формы. Значение истинности высказываний и высказывательных форм. Простые и составные высказывания и высказывательные формы. Логическая структура составного предложения. Конъюнкция и дизъюнкция высказываний Таблица истинности высказываний. Конъюнкция и дизъюнкция высказывательных форм. Высказывания с кванторами. Квантор общности и значение истинности. Квантор существования и значение истинности. Отрицание высказываний и высказывательных форм. Отношения следования и равносильности. Структура и виды теорем. Теорема, правила, формулы Виды теорем. Закон контрпозиции Основные выводы
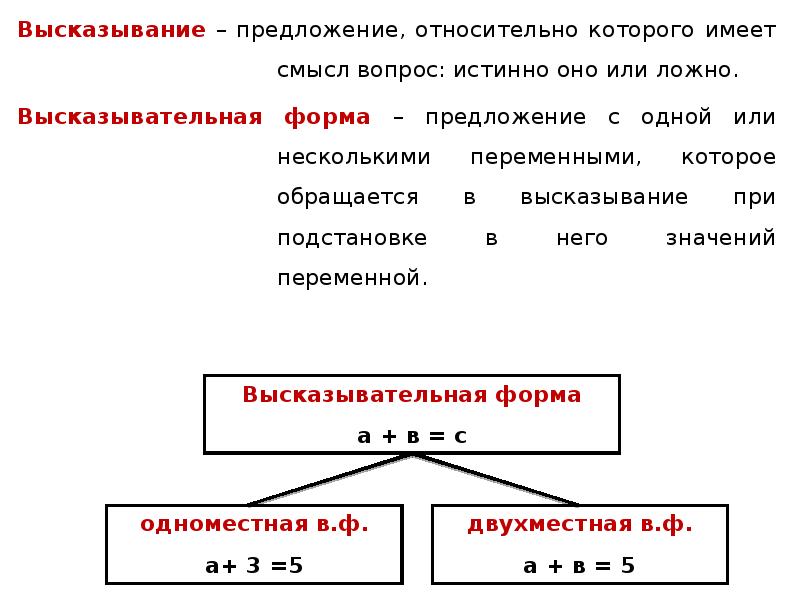
Высказывание – предложение, относительно которого имеет смысл вопрос: истинно оно или ложно. Высказывание – предложение, относительно которого имеет смысл вопрос: истинно оно или ложно. Высказывательная форма – предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке в него значений переменной.
Составим таблицу истинности конъюнкции и дизъюнкции Составим таблицу истинности конъюнкции и дизъюнкции
Конъюнкцию одноместных высказывательных форм обозначают: Конъюнкцию одноместных высказывательных форм обозначают: А(х) В(х) Высказывательная форма А(х) В(х) обращается в истинное высказывание, если обращаются в истинное высказывание обе высказывательные формы А(х) и В(х) при значениях х из области определения Х. Пример: х + 3 13 А(х) – х+313 3х 15 В(х) – 3х 15 Логическая структура А(х) В(х) х 10 х 5
Определение. Отрицанием высказывания А называется высказывание Ā, которое ложно, если высказывание А истинно, и истинно, если высказывание А- ложно. Определение. Отрицанием высказывания А называется высказывание Ā, которое ложно, если высказывание А истинно, и истинно, если высказывание А- ложно.
Определение. Предложения А(х) и В(х) равносильны, если из предложения А(х) следует предложения В(х), а из предложения В(х) следует предложение А(х). Определение. Предложения А(х) и В(х) равносильны, если из предложения А(х) следует предложения В(х), а из предложения В(х) следует предложение А(х). Обозначение: А(х)В(х) Читают: А(х) равносильно В(х) А(х) тогда и только тогда, когда В(х) А(х) – необходимое и достаточное условие В(х) В(х) – необходимое и достаточное условие А(х)
Теорема – это высказывание, истинность которого устанавливается путем доказательства. Теорема – это высказывание, истинность которого устанавливается путем доказательства. Логическая структура теоремы: АВ, где А и В – высказывательные формы с одной или несколькими переменными. Предложение А – условие теоремы; В – заключение. Теорема. Если а – любое число и n, k – натуральные числа, то справедливо равенство

Определение. Отрицанием высказывания А называется высказывание , которое ложно, когда высказывание А истинно, и истинно, когда высказывание А – ложно.
Таблица истинности отрицания имеет вид:

Из данного определения следует, что предложение и его отрицание не могут быть ни одновременно истинны, ни одновременно ложны.
а) Число 28 не делится на 9.
б) Неверно, что число 28 делится 9.
Высказывания, которые мы получили, истинные. Значит, отрицание данного предложения построено правильно.
Можно доказать, что отрицание конъюнкции двух высказываний А и В является дизъюнкцией их отрицаний. Для этого надо убедится в том, что значения истинности высказываний вида и совпадают при любых значениях истинности высказываний А и В. Сделать это можно при помощи таблицы истинности:



Про высказывания вида и говорят, что ониравносильны, и пишут .
Аналогично можно доказать, что имеет место равносильность .
Эти равносильности носят название законов де Моргана.
Решение (два способа).
Вообще если дано предложение (х) А(х), то его отрицанием будут предложения и (х) , также имеющие один и тот же смысл (и одно и то же значение истинности).
Получаем две равносильности: (х) ;
х) .
Из них вытекает правило: для того чтобы построить отрицание высказывания, начинающегося с квантора общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора.
Решение. Сделать это можно двумя способами.
Последнее, о чем пойдет речь, - это отрицание высказывательных форм.
Доказательство этого равенства мы опускаем.
Читайте также:
- Сценарий праздника про насекомых в детском саду
- Концепция профильного обучения в школе
- Сценарий сказки 12 месяцев для детского сада подготовительная группа
- Выбор родительского комитета на родительском собрании в детском саду старшая группа
- Методическая разработка викторина по познавательному развитию в доу

