По какой формуле можно определить объем тела кратко

Обновлено: 02.07.2024

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Объемы геометрических тел

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

V сохраняется при движениях.
V удовлетворяет принципу Кавальери.
Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

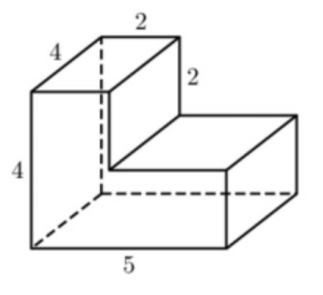
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

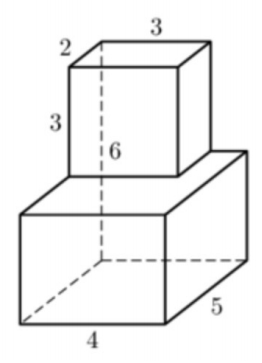
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Разберем, как можно вычислять объемы изучаемых в школе фигур.

Объем призмы

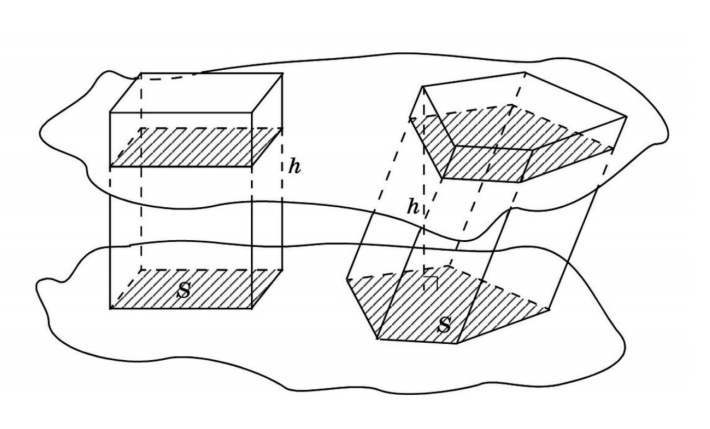
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

V S_осн h

Задачник является Частью УМК для 10-11 классов, предназначенного для изучения предмета на углубленном уровне, и содержит более 1000 задач разной степени трудности, помогающих изучению и усвоению материала, изложенного в учебнике. Пособие соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования.

Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

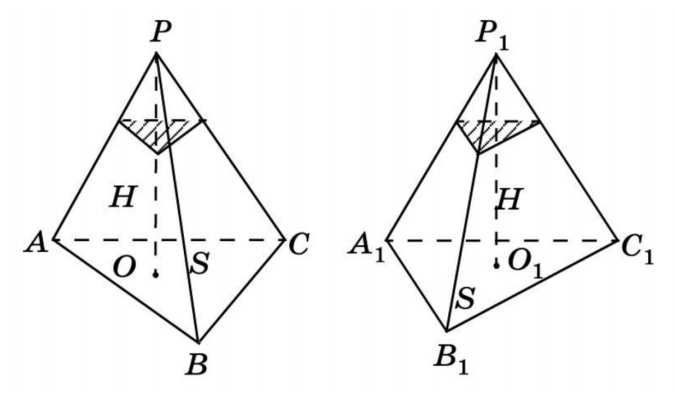
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V ₁/V₂ = 1 V₁= V₂

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

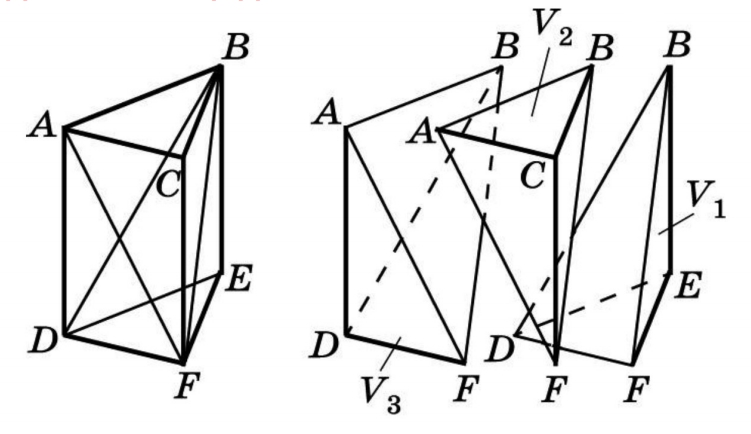
V_призмы S h = 3V

Объем цилиндра

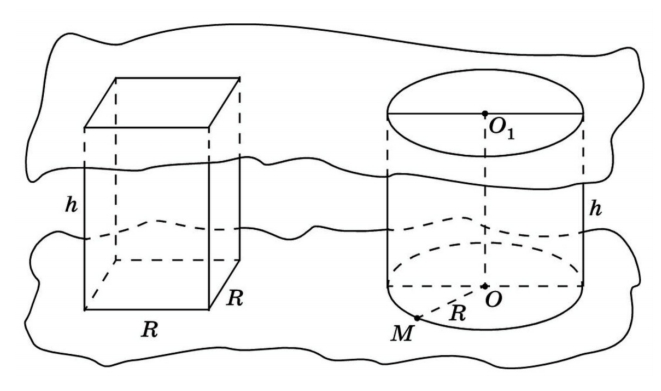
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

V_цил = πh × R 2

Объем конуса

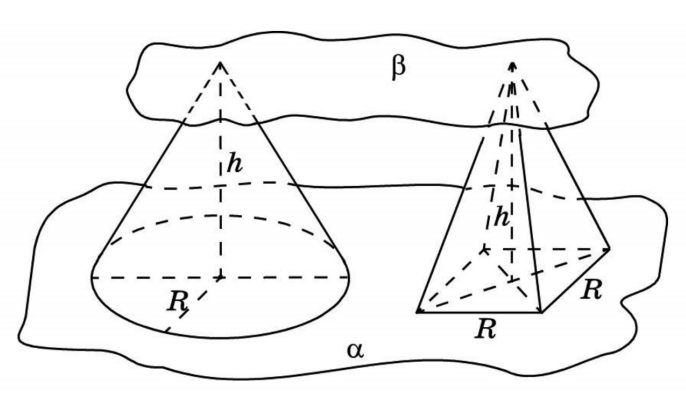
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

S_Ф1/S_Ф2 = π

V_конуса = 1/3 πR 2 h

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR 2 . Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x 2 . Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R 2 — x 2 ).

Заметим, что: πR 2 + πR 2 — πR 2 = πR 2

V_цил = πR 2 × R = πR 3 = 1/3 R 3 π + V_шара

V_шара = 4/3 πR 3

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

- количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба:

Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

Объем параллелепипеда

Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

Объем пирамиды

Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды:

Объем правильного тетраэдра

Формула объема правильного тетраэдра:

Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра:

где V - объем цилиндра,
S_o - площадь основания цилиндра,
R - радиус цилиндра,
h - высота цилиндра,
π = 3.141592.

Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса:

где V - объем конуса,
S_o - площадь основания конуса,
R - радиус основания конуса,
h - высота конуса,
π = 3.141592.

Объем шара

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.

Формула объема шара:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Все формулы объема геометрических тел

Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба:

V = a 3

V - объем куба,
a - длина грани куба.

Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

V- объем призмы,
S_o - площадь основания призмы,
h - высота призмы.

Объем параллелепипеда

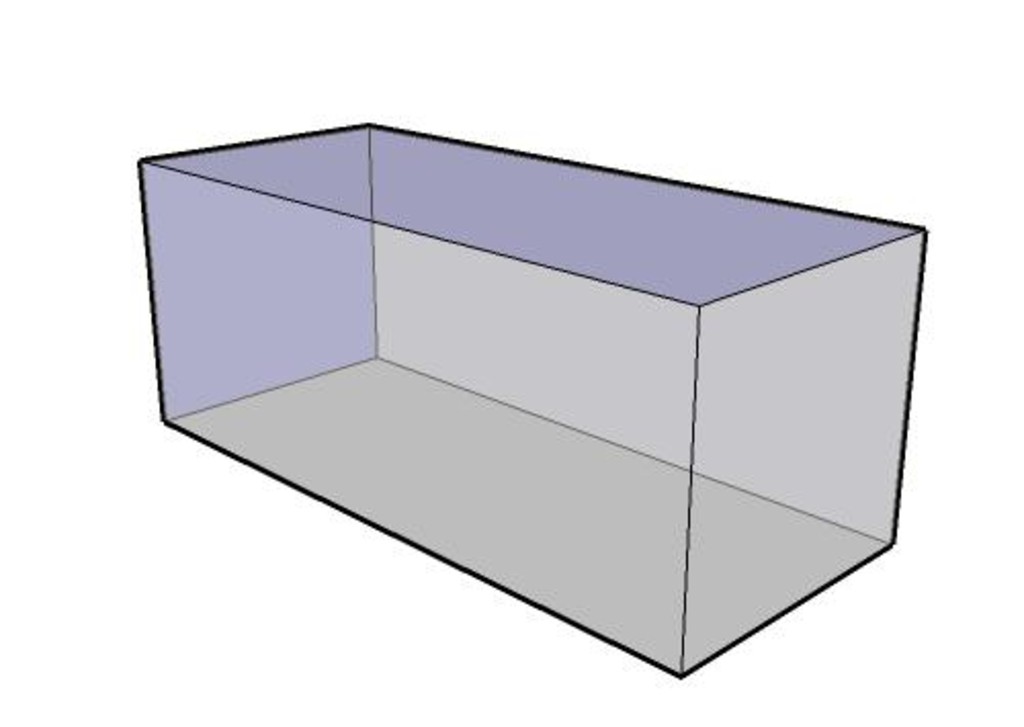
Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

V- объем параллелепипеда,
S_o - площадь основания,
h - длина высоты.

Объем пирамиды

Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).

Формула объема пирамиды:

V - объем пирамиды,
S_o - площадь основания пирамиды,
h - длина высоты пирамиды.

Объем усеченной пирамиды

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S₁(abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

Формула объема усеченной пирамиды:

S1 - площадь верхнего основания усеченной пирамиды,
S2 - площадь нижнего основания усеченной пирамиды,
h - высота усеченной пирамиды.

Объем цилиндра

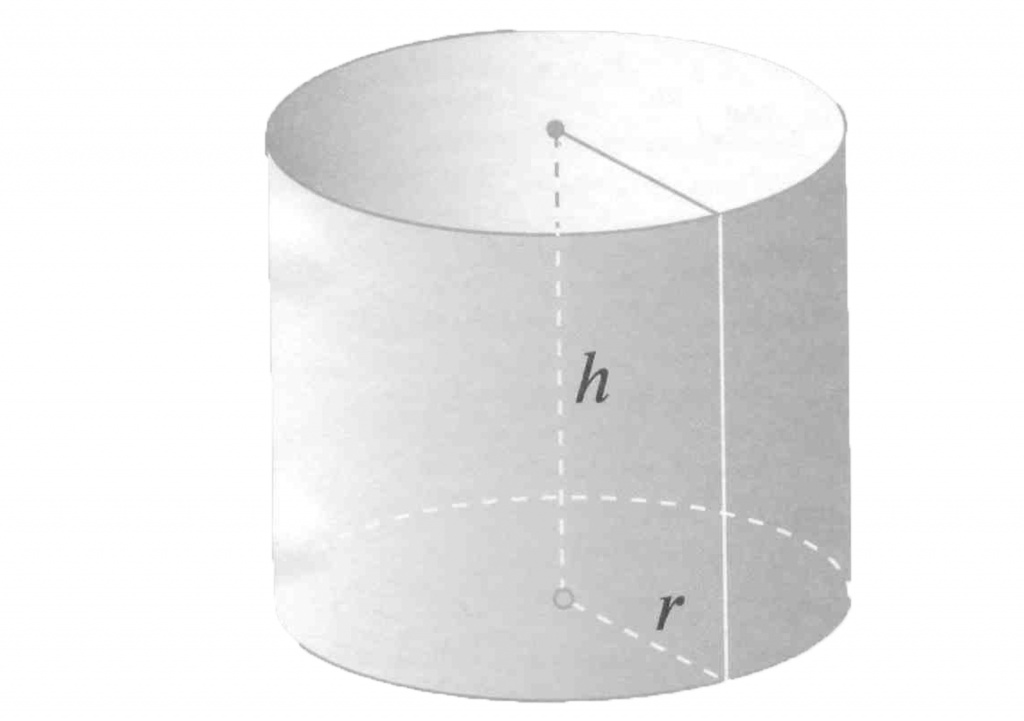
Объем цилиндра равен произведению площади его основания на высоту.

Формула объема цилиндра:

V= π R 2 h

V= S_оh

V - объем цилиндра,
S_o - площадь основания цилиндра,
R - радиус цилиндра,
h - высота цилиндра,
π = 3.141592

Объем правильной треугольной пирамиды

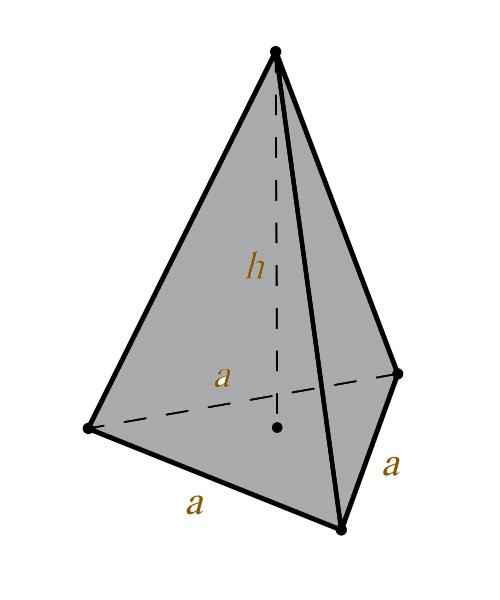
Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS).

Формула объема правильной треугольной пирамиды:

V - объем пирамиды;
h - высота пирамиды;
a - сторона основания пирамиды.

Объем конуса

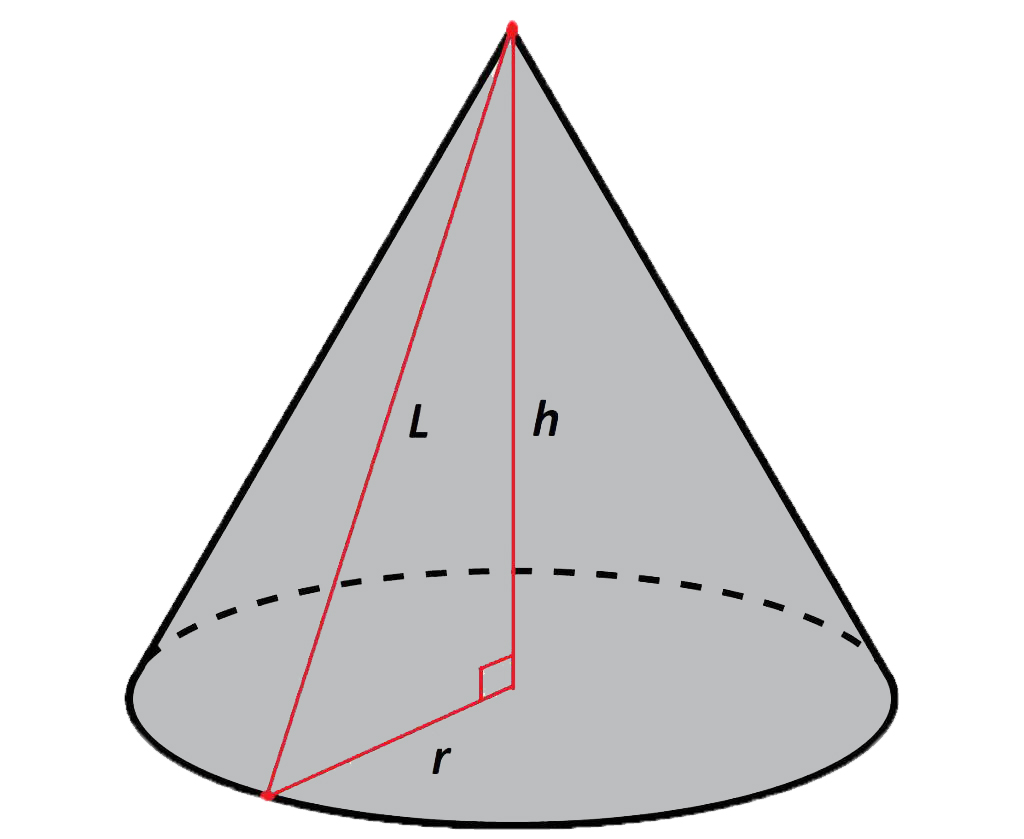
Объем круглого конуса равен трети произведения площади основания S на высоту H.

Формула объема конуса:

V - объем конуса;
R - радиус основания;
H - высота конуса;
I - длина образующей;
S - площадь боковой поверхности конуса.

Объем усеченного конуса

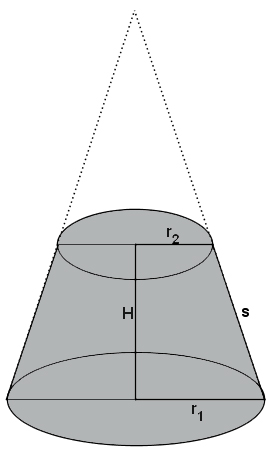
Объем усеченного конуса равен разности объемов двух полных конусов.

Формула объема усеченного конуса:

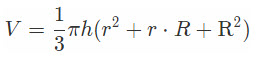
V - объем усеченного конуса;
H - высота усеченного конуса;
R и R 2 - радиусы нижнего и верхнего оснований.

Объем тетраэдра

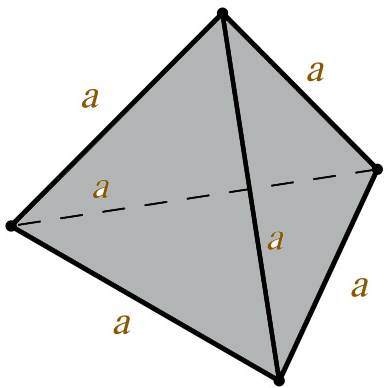
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

Формула тетраэдра:

V - объем тетраэдра;
a - ребро тетраэдра.

Объем шара

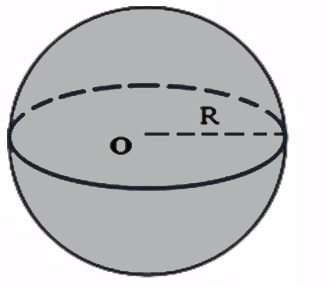
Объем шара равен четырем третьим от его радиуса в кубе перемноженного на число пи.

Формула объема шара:

V - объем шара;
R - радиус шара;
S - площадь сферы.

Объем шарового сегмента и сектора

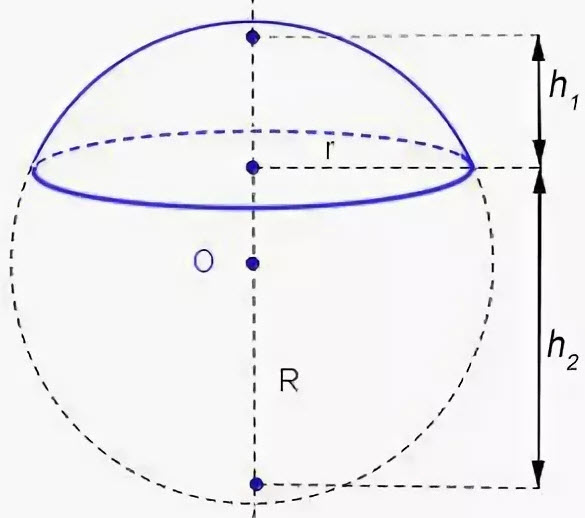
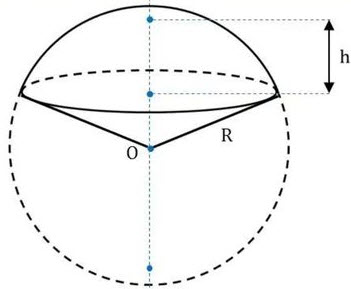
Шаровый сегмент - это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

Формула объема шарового сегмента:

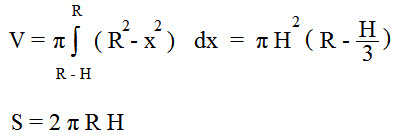
R - радиус шара
H - высота сегмента
π ≈ 3,14

Формула объема шарового сектора:

h - высота сегмента
R - радиус шара
π ≈ 3,14

Объем прямоугольного параллелепипеда

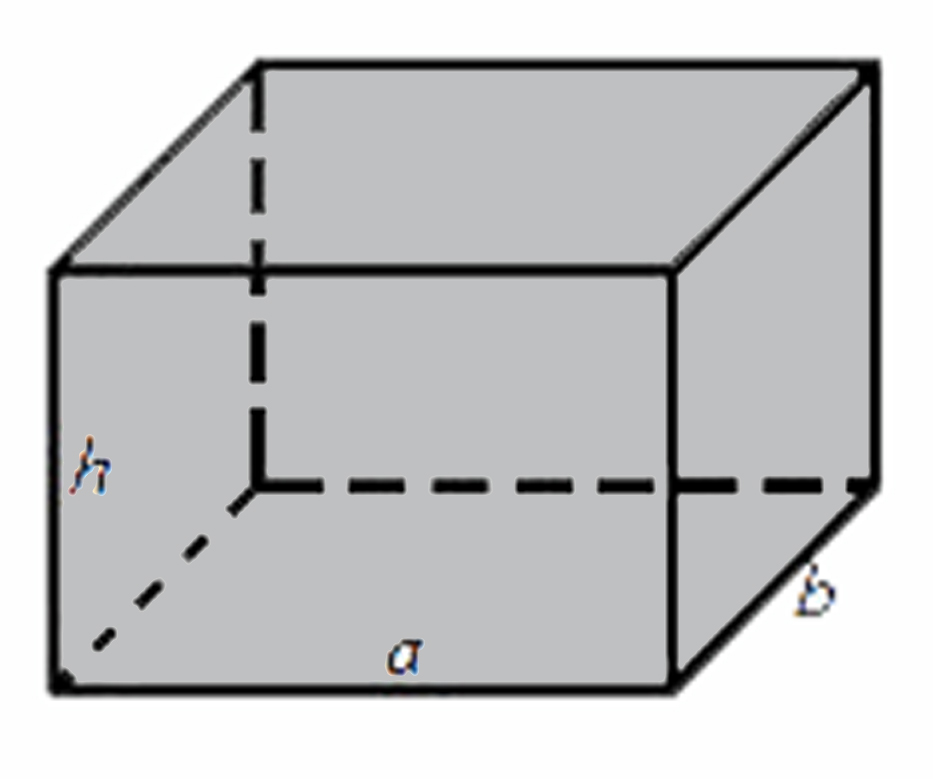
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

V - объем прямоугольного параллелепипеда,
a - длина,
b - ширина,
h - высота.

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 27 человек(а).

Количество источников, использованных в этой статье: 11. Вы найдете их список внизу страницы.

Объем – это количество занимаемого телом пространства, а плотность равна массе тела, поделенной на его объем. [1] X Источник информации Прежде чем вычислить плотность тела, необходимо найти его объем. Если тело имеет правильную геометрическую форму, его объем можно рассчитать при помощи простой формулы. Объем измеряется обычно в кубических сантиметрах (см 3 ) или кубических метрах (м 3 ). Используя найденный объем тела, легко рассчитать его плотность. Для измерения плотности служат граммы на кубический сантиметр (г/см 3 ) или граммы на миллилитр (г/мл).

Читайте также: