Около какого правильного многоугольника можно описать окружность кратко

Обновлено: 04.07.2024

Дано: А₁А₂А₃. А_n - правильный многоугольник.

Доказательство:

Пусть точка О - точка пересечения биссектрис углов А₁ и А₂. Соединим точку О отрезками с остальными вершинами многоугольника и докажем, что ОА₁ = ОА₂ = . = ОА_n.

А₁А₂А₃. А_n - правильный многоугольник, значит, А₁ = А₂, тогда 1 = 3 (т.к. ОА₁ и ОА₂ биссектрисы равных углов А₁ и А₂), следовательно,

А₁ОА₂ - равнобедренный (по признаку равнобедренного треугольника), поэтому ОА₁ = ОА₂.

А₁ОА₂ = А₂ОА₃ по двум сторонам и углу между ними (А₁А₂ = А₂А₃ как стороны правильного многоугольника, ОА₂ - общая, 3 = 4, т.к. ОА₂ биссектриса угла А₂), следовательно,

ОА₁ = ОА₃. Аналогично можно доказать, что ОА₂ = ОА₄, ОА₃ = ОА₅ и т.д.

Итак, ОА₁ = ОА₂ = . = ОА_n, значит, точка О равноудалена от всех вершин многоугольника. Поэтому окружность с центром О и радиусом ОА₁ является описанной около многоугольника А₁А₂А₃. А_n.

Докажем, что описать можно только одну окружность.

Рассмотрим какие-нибудь три вершины многоугольника А₁А₂А₃. А_n, например, А₁, А₂, А₃. Мы можем начертить только одну окружность одновременно проходящую через три точки А₁, А₂, А₃ (смотри доказательство), т.е. другой окружности проходящей через три данные точки не существует, значит, около многоугольника А₁А₂А₃. А_n можно описать только одну окружность, т.к. точки А₁, А₂, А₃ - вершины данного многоугольника. Теорема доказана.

Этот урок поможет вспомнить, какую окружность называют описанной около многоугольника. Будет доказана теорема об окружности, описанной около правильного многоугольника. А также рассмотрены задачи на применение полученных знаний.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Окружность, описанная около правильного многоугольника"

На этом уроке мы вспомним, какую окружность называют описанной около многоугольника. Докажем теорему об окружности, описанной около правильного многоугольника.

Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны. Так как у правильного многоугольника все углы равны, то угол правильного n-угольника можно вычислить по формуле: альфа энное равно 180 градусов умножить на эн минус два деленное на н, где n – количество сторон (углов) правильного n-угольника.

И вспомним еще определение описанной окружности.

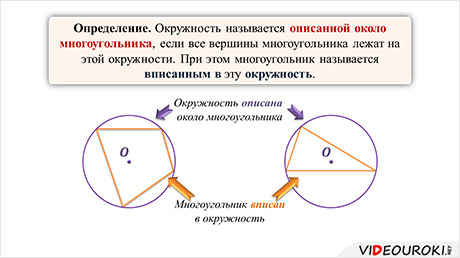
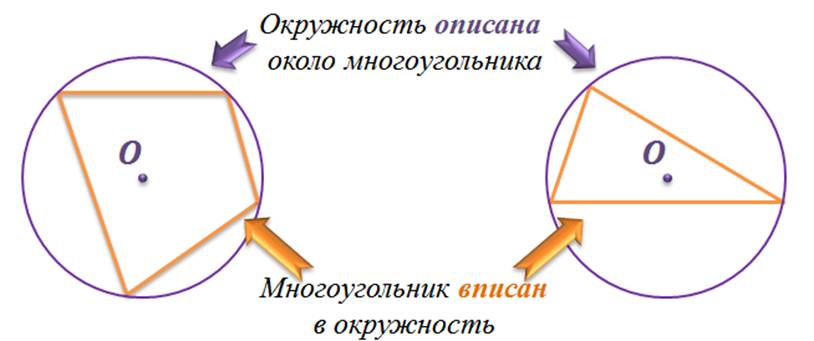
Определение. Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на этой окружности. При этом многоугольник называется вписанным в эту окружность.

Докажем теорему об окружности, описанной около правильного многоугольника.

Теорема. Около любого правильного многоугольника можно описать окружность, и притом только одну.

Доказательство.

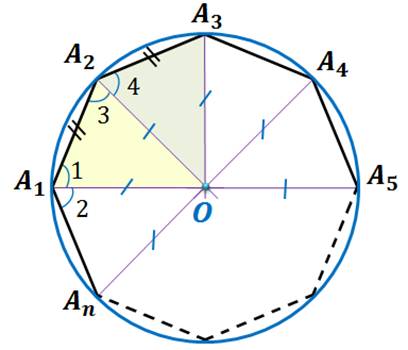
Пусть – правильный многоугольник.

Рассмотрим .

Так как ,то .

Следовательно, – равнобедренный.

Значит, .

Рассмотрим и .

– общая сторона и .

Следовательно, по двум сторонам и углу между ними.

Отсюда, .

Тогда точка равноудалена от всех вершин многоугольника.

Значит, окружность с центром в точке и радиусом является описанной

Тогда точка равноудалена от всех вершин многоугольника.

Значит, окружность с центром в точке и радиусом является описанной около многоугольника.

Рассмотрим вершины , и .

Так как через эти точки проходит только одна окружность, можно описать только одну окружность.

Теорема доказана.

Задача. Правильный многоугольник вписан в окружность с центром в точке . Длина одной стороны многоугольника равна см. Найдите периметр правильного многоугольника , если .

Решение. Так как у правильного многоугольника все стороны равны, то для нахождения периметра нужно знать число его сторон.

Пусть многоугольник имеет сторон.

Рассмотрим .

Точка равноудалена от всех вершин многоугольника.

Значит, .

Следовательно, – равнобедренный.

(см)

Ответ: (см).

Подведем итоги урока. На этом уроке доказали теорему об окружности, описанной около правильного многоугольника. А именно, что около любого правильного многоугольника можно описать окружность, и притом только одну.

Например, на рисунке 8.106 .

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.

$LaTeX formula: \angle A+\angle C=\angle B+\angle D=180^<\circ> Например, на рисунке 8.107$
.

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);

3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Радиус окружности, описанной около многоугольника, как правило, обозначают , а радиус окружности, вписанной в многоугольник, обозначают :

1) для равностороннего треугольника со стороной :

$LaTeX formula: R=\frac<\sqrt<3> >$
, (8.34)

$LaTeX formula: r=\frac<2\sqrt<3> >$
; (8.35)

2) для произвольного треугольника со сторонами и площадью :

$LaTeX formula: r=\frac<2S> $
; (8.37)

3) для прямоугольного треугольника с катетами и гипотенузой :

$LaTeX formula: R=\frac<c> $
, (8.38)

4) для квадрата со стороной и диагональю :

$LaTeX formula: R=\frac<d> $
, (8.40)

$LaTeX formula: r=\frac<2> $
; (8.41)

5) для прямоугольника с диагональю :

$LaTeX formula: R=\frac<d> $
; (8.42)

6) для ромба с высотой :

$LaTeX formula: r=\frac<h> $
; (8.43)

7) для трапеции с высотой , при условии, что в трапецию можно вписать окружность:

$LaTeX formula: r=\frac<h> $
. (8.44)

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами и площадью , по формуле " height="" />
найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);

8) для правильного шестиугольника со стороной :

, (8.45)

Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка является центром вписанной в него и описанной около него окружностей.

$LaTeX formula: 2\pi -8$

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна .

Решение. Так как площадь круга радиуса находят по формуле 8.32 , а площадь квадрата со стороной находят по формуле " height="" />
, то согласно условию задачи запишем: -S_=12" height="" />
, -a^=2\pi -8" height="" />
.

$LaTeX formula: 2\sqrt<2> Ответ:$
.

Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами и находят по формуле .

Пусть , тогда (рис. 8.118).

Получим: , +3x-4=0" />
, откуда , следовательно, , .

По теореме Пифагора найдем диагональ прямоугольника: =1+16=17" />
, " />
. Согласно формуле 8.42 " />
.

$LaTeX formula: 0,5\sqrt<17> Ответ:$
.

=\left (\frac> \right )^+\left ( \frac \right )^" />
, =3^+4^" />
, .

По формуле d_d_" />
найдем площадь ромба: \cdot 6\cdot 8=24" />
.

Но площадь ромба можно найти и по формуле , а так как , то . Тогда , а .

$LaTeX formula: 4\sqrt<3> Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна$
.

Решение. Площадь правильного треугольника со стороной находят по формуле: a^>" />
.

Зная площадь треугольника, найдем его сторону: a^>=4\sqrt" />
, =16" />
, .

$LaTeX formula: r=\frac<4> По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: >=\frac>$
.

$LaTeX formula: C=\frac<4\pi > По формуле 8.30 найдем длину окружности: >$
.

$LaTeX formula: \frac<4\sqrt Ответ: \pi >$
.

Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.

Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой находят по формуле 8.38 . Тогда .

Так как треугольник равнобедренный, то его катеты и раны и по теореме Пифагора =2a^" height="" />
, откуда <\sqrt>" height="" />
, <\sqrt>=2\sqrt" height="" />
.

Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае " />
, -4>=2\sqrt-2" />
.

$LaTeX formula: 2\sqrt<2> Ответ: -2$
.

Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник . Точка является центром вписанной в треугольник окружности (рис. 8.120).

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат со стороной 3. Если катет , а сторона квадрата , то .

Пусть отрезок . По свойству касательных и .

Тогда по теореме Пифагора =AC^+AB^" height="" />
или =64+9+6x+x^" height="" />
, откуда , .

Найдем катет : .

Найдем площадь треугольника: =\frac\cdot AC\cdot AB" />
, =\frac\cdot 8\cdot 15=60" />
.

Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).

Решение. Согласно свойству биссектрисы треугольника запишем: =\frac" />
, откуда .

В свою очередь по формуле Герона " />
найдем площадь треугольника. Так как , то =9\sqrt" />
.

$LaTeX formula: r=\frac<18\sqrt Тогда >=\frac>=0,6\sqrt$
.

$LaTeX formula: 0,6\sqrt<15> Ответ:$
.

Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.

Решение. Согласно условию задачи и рисунку 8.122, запишем: , .

По свойству четырехугольника, описанного около окружности, получим: , , .

Согласно формуле (a+b)h" />
найдем площадь трапеции: \cdot 15\cdot 6=45" />
.

Пример 9. Длины оснований равнобедренной трапеции относятся как , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.

Решение. Рассмотрим равнобедренную трапецию (рис. 8.123) и проведем диагональ трапеции .

Радиус окружности, описанной около треугольника , найдем по формуле 8.36 :

>=\frac\cdot AD\cdot BN>" />
, " />
.

Зная, что и вводя коэффициент пропорциональности , получим , .

Так как длина средней линии трапеции равна высоте трапеции, то (5k +12k)=17" />
, откуда . Тогда , .

Поскольку четырехугольник является прямоугольником, то , тогда (24-10)=7" height="" />
.

+ND^>" />
, +17^>=17\sqrt" />
.

По формуле 8.36 найдем радиус окружности, описанной около треугольника , а, следовательно, и около трапеции :

$LaTeX formula: R=\frac<\sqrt<338> \cdot 17\sqrt>=\frac=13$
.

$LaTeX formula: S=169\pi$

Согласно формуле 8.32 найдем площадь круга: .

$LaTeX formula: 169\pi$

Ответ: .

$LaTeX formula: \sqrt<3> Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна$
.

$LaTeX formula: R=a=\sqrt<3> Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника:$
.

По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как " />
, то " />
.

Площадь круга находят по формуле 8.32. Тогда =3\pi" />
, а =\frac<9\pi>" />
.

Найдем площадь кольца: =S_-S_" />
, =3\pi -\frac<9\pi >=\frac<3\pi >" />
.

$LaTeX formula: 0,75\pi$

Ответ: .

1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.

3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.

5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.

Длину окружности радиуса находят по формуле:

$LaTeX formula: C=2\pi R$

. (8.30)

Площадь круга радиуса находят по формуле:

$LaTeX formula: S=\pi R^<2> $
. (8.32)

Вокруг любого правильного многоугольника можно описать окружность и только одну.

Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам многоугольника.

Площадь многоугольника будет максимальной, если он вписан в окружность.

Свойства окружности, описанной около треугольника

Вокруг любого треугольника можно описать окружность, причем только одну.
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.

$R=\frac<AB> =\frac=\frac$

Свойства окружности, описанной около четырехугольника

$S=\sqrt<(p-a)(p-b)(p-c)(p-d)> $

Примеры решения задач

$BC=\sqrt<A< ^>+A^>>=\sqrt=5 \ cm$

$R=\frac<1> Тогда BC=2,5$
см.

Задание	Вокруг четырехугольника описана окружность. Угол меньше угла в 2 раза, а угол больше угла в три раза. Найти углы четырехугольника.
Решение	Введем обозначения: пусть , тогда и , тогда . Так как четырехугольник вписан в окружность, то сумма его противоположных углов равна :

$\begin & x+3y=180, \\ & 2x+y=180. \\ \end$

Решив эту систему, получим . Следовательно,

$\angle A= ^>,\ \angle B=2\cdot ^>=^>,\ \angle D=^>,\ \text\ \angle C=3\cdot ^>=^>$

Читайте также: