Что такое синус кратко определение
Обновлено: 04.07.2024
У многих учеников возникают проблемы с этой темой, в основном, из-за непонимания общего смысла тригонометрии. В этой статье я постараюсь помочь вам разобраться зачем нужна тригонометрия и расскажу про лайфхак, чтобы не учить значения синуса и косинуса.
К моменту начала изучения тригонометрии Вы, скорее всего, уже знаете: определение прямоугольного треугольника и окружности — этого вполне достаточно для понимания темы.
*прошу заметить, что некоторые формулировки могут не соответствовать действительности - это сделано для того, чтобы вы лучше запомнили основы. Точные понятия и определения расскажет ваш учитель математики.
Что такое синус и косинус?
Изначально не было никакой окружности. Изучая треугольники, древние ученые выражали углы через соотношение сторон. То-есть синусы и косинусы появились раньше градусной меры углов.
Поскольку угол может быть найден через разные соотношения сторон, решили дать им названия: синус и косинус.
Синус - это отношение стороны треугольника, лежащей напротив данного угла, к гипотенузе (большей стороне).
Косинус - это отношение прилежащей стороны к гипотенузе.
Думаю не ошибусь, если скажу, что теорема Пифагора - самая полезная теорема в геометрии. Давайте применим её для данного треугольника:
Понятия синуса, косинуса, тангенса, котангенса неразрывно связаны с понятием угла.
Звучит ужасно, да?
Не так страшен черт, как его малюют!
Чтобы хорошо разобраться в этих понятиях (нет, не в чёрте! в тригонометрии 🙂 ), начнём с самого начала.
Синус, косинус, тангенс, котангенс — коротко о главном.
Синус угла — это отношение противолежащего (дальнего) катета к гипотенузе
Косинус угла — это отношение прилежащего (близкого) катета к гипотенузе
Тангенс угла — это отношение противолежащего (дальнего) катета к прилежащему (близкому)
Котангенс угла — это отношение прилежащего (близкого) катета к противолежащему (дальнему).
Понятие угла: радиан, градус
Давай для начала разберёмся в понятии угла.
Посмотрим на рисунок.
![]()
Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!
Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.
Углом в \( 1<>^\circ \) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную \( \frac\) части окружности.
![]()
То есть на рисунке выше изображён угол \( \beta \), равный \( 50<>^\circ \), то есть этот угол опирается на круговую дугу размером \( \frac\) длины окружности.
Углом в \( 1\) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.
Ну что, разобрался? Если нет, то давай разбираться по рисунку.
![]()
Итак, на рисунке изображён угол \( \gamma \), равный \( 1\) радиану.
То есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина \( AB\) равна длине \( BB’\) или радиус \( r\) равен длине дуги \( l\)).
Таким образом, длина дуги вычисляется по формуле:
\( l=\theta \cdot r\), где \( \theta \) — центральный угол в радианах.
Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью?
Да, для этого надо вспомнить формулу длины окружности. Вот она:
Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен \( 2\pi \).
То есть, соотнеся величину в градусах и радианах, получаем, что \( 2\pi =360<>^\circ \).
Соответственно, \( \pi =180<>^\circ \).
А сколько радиан составляют \( 60<>^\circ \)?
Уловил? Тогда вперёд закреплять:
Тогда смотри ответы:
Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике
Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?
Давай разбираться. Для этого нам поможет прямоугольный треугольник.
![]()
Как называются стороны прямоугольного треугольника?
Всё верно, гипотенуза и катеты.
Гипотенуза — это сторона, которая лежит напротив прямого угла (в нашем примере это сторона \( AC\))
Катеты – это две оставшиеся стороны \( AB\) и \( BC\) (те, что прилегают к прямому углу).
Причём, если рассматривать катеты относительно угла \( \angle BAC\), то катет \( AB\) – это прилежащий катет, а катет \( BC\) — противолежащий.
Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.
В нашем треугольнике \( \sin \beta =\frac\).
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.
В нашем треугольнике \( \cos \beta =\frac\).
Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
В нашем треугольнике \( tg\beta =\frac\).
Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).
В нашем треугольнике \( ctg\beta =\frac\).
Эти определения необходимо запомнить!
Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе.
А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:
В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).
Тогда убедись, посмотрев на рисунок:
![]()
Рассмотрим, к примеру, косинус угла \( \beta \).
По определению, из треугольника \( ABC\): \( \cos \beta =\frac=\frac=\frac\).
Но ведь мы можем вычислить косинус угла \( \beta \) и из треугольника \( AHI\): \( \cos \beta =\frac=\frac=\frac\).
Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.
Если разобрался в определениях, то вперёд закреплять их!
Для треугольника \( ABC\), изображённого ниже на рисунке, найдём \( \sin \ \alpha ,\ \cos \ \alpha ,\ tg\ \alpha ,\ ctg\ \alpha \).
![]()
Тогда пробуй сам: посчитай то же самое для угла \( \beta \).
Ответы: \( \sin \ \beta =0,6;\ \cos \ \beta =0,8;\ tg\ \beta =0,75;\ ctg\ \beta =\frac\).
Единичная (тригонометрическая) окружность
Разбираясь в понятиях градуса и радиана, мы рассматривали окружность с радиусом, равным \( 1\).
Такая окружность называется единичной. Еще ее называют тригонометрической. Это одно и тоже.
Эта окружность — универсальная шпаргалка для решения уравнений и даже неравенств, если уметь ей пользоваться!
Здесь мы тоже ее разберем довольно подробно.
![]()
Как можно заметить, данная окружность построена в декартовой системе координат.
Радиус окружности равен единице.
При этом центр окружности лежит в начале координат, начальное положение радиус-вектора зафиксировано вдоль положительного направления оси \( x\) (в нашем примере, это радиус \( AB\)).
Каждой точке окружности соответствуют два числа: координата по оси \( x\) и координата по оси \( y\).
А что это за числа-координаты? И вообще, какое отношение они имеют к рассматриваемой теме?
Для этого надо вспомнить про рассмотренный прямоугольный треугольник.
На рисунке, приведённом выше, можно заметить целых два прямоугольных треугольника.
Рассмотрим треугольник \( ACG\). Он прямоугольный, так как \( CG\) является перпендикуляром к оси \( x\).
Чему равен \( \cos \ \alpha \) из треугольника \( ACG\)?
Всё верно \( \cos \ \alpha =\frac\).
Кроме того, нам ведь известно, что \( AC\) – это радиус единичной окружности, а значит, \( AC=1\).
Подставим это значение в нашу формулу для косинуса. Вот что получается:
А чему равен \( \sin \ \alpha \) из треугольника \( ACG\)?
Ну конечно, \( \sin \alpha =\frac\)!
Подставим значение радиуса \( AC\) в эту формулу и получим:
Так, а можешь сказать, какие координаты имеет точка \( C\), принадлежащая окружности? Ну что, никак?
А если сообразить, что \( \cos \ \alpha \) и \( \sin \alpha \) — это просто числа?
Какой координате соответствует \( \cos \alpha \)?
Ну, конечно, координате \( x\)!
А какой координате соответствует \( \sin \alpha \)?
Всё верно, координате \( y\)!
Таким образом, точка \( C(x;y)=C(\cos \alpha ;\sin \alpha )\).
![]()
А чему тогда равны \( tg \alpha \) и \( ctg \alpha \)?
Всё верно, воспользуемся соответствующими определениями тангенса и котангенса и получим, что \( tg \alpha =\frac=\frac\), а \( ctg \alpha =\frac=\frac\).
А что, если угол будет больше \( 90<>^\circ =\frac<\pi >\)?
Вот, к примеру, как на этом рисунке:
![]()
Что же изменилось в данном примере?
Давай разбираться. Для этого опять обратимся к прямоугольному треугольнику.
Чему равно значение синуса, косинуса, тангенса и котангенса для угла \( _><_>G=180<>^\circ -\beta \ \)?
Всё верно, придерживаемся соответствующих определений тригонометрических функций:
Ну вот, как видишь, значение синуса угла всё так же соответствует координате \( y\); значение косинуса угла – координате \( x\); а значения тангенса и котангенса соответствующим соотношениям.
Таким образом, эти соотношения применимы к любым поворотам радиус-вектора.
Уже упоминалось, что начальное положение радиус-вектора – вдоль положительного направления оси \( x\).
До сих пор мы вращали этот вектор против часовой стрелки, а что будет, если повернуть его по часовой стрелке?
Ничего экстраординарного, получится так же угол определённой величины, но только он будет отрицательным.
Таким образом, при вращении радиус-вектора против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке – отрицательные.
Итак, мы знаем, что целый оборот радиус-вектора по окружности составляет \( 360<>^\circ \) или \( 2\pi \).
А можно повернуть радиус-вектор на \( 390<>^\circ \) или на \( -1140<>^\circ \)?
Ну конечно, можно!
В первом случае, \( 390<>^\circ =360<>^\circ +30<>^\circ \), таким образом, радиус-вектор совершит один полный оборот и остановится в положении \( 30<>^\circ \) или \( \frac<\pi >\).
Во втором случае, \( -1140<>^\circ =-360<>^\circ \cdot 3-60<>^\circ \), то есть радиус-вектор совершит три полных оборота и остановится в положении \( -60<>^\circ \) или \( -\frac<\pi >\).
Таким образом, из приведённых примеров можем сделать вывод, что углы, отличающиеся на \( 360<>^\circ \cdot m\) или \( 2\pi \cdot m\) (где \( m\) – любое целое число), соответствуют одному и тому же положению радиус-вектора.
Ниже на рисунке изображён угол \( \beta =-60<>^\circ \).
Это же изображение соответствует углу \( -420<>^\circ ,-780<>^\circ ,\ 300<>^\circ ,660<>^\circ \) и т.д.
Этот список можно продолжить до бесконечности.
Все эти углы можно записать общей формулой \( \beta +360<>^\circ \cdot m\) или \( \beta +2\pi \cdot m\) (где \( m\) – любое целое число)
![]()
Теперь, зная определения основных тригонометрических функций и используя единичную окружность, попробуй ответить, чему равны значения:
Вот тебе в помощь единичная окружность:
![]()
Возникли трудности? Тогда давай разбираться.
Итак, мы знаем, что:
Отсюда мы определяем координаты точек, соответствующих определённым мерам угла.
Ну что же, начнём по порядку: углу в \( 90<>^\circ =\frac<\pi >\) соответствует точка с координатами \( \left( 0;1 \right)\), следовательно:
\( \text\ 90<>^\circ =\frac=\frac\Rightarrow \text\ 90<>^\circ \) — не существует;
Дальше, придерживаясь той же логики, выясняем, что углам в \( 180<>^\circ ,\ 270<>^\circ ,\ 360<>^\circ ,\ 450<>^\circ (=360<>^\circ +90<>^\circ )\ \) соответствуют точки с координатами \( \left( -1;0 \right),\text< >\left( 0;-1 \right),\text< >\left( 1;0 \right),\text< >\left( 0;1 \right)\), соответственно.
Зная это, легко определить значения тригонометрических функций в соответствующих точках. Сначала попробуй сам, а потом сверяйся с ответами.
Ответы:
\( \displaystyle \sin \ 180<>^\circ =\sin \ \pi =0\) \( \displaystyle \cos \ 180<>^\circ =\cos \ \pi =-1\) \( \text\ 180<>^\circ =\text\ \pi =\frac=0\)
\( \text\ 180<>^\circ =\text\ \pi =\frac\Rightarrow \text\ \pi \) — не существует
\( \sin \ 270<>^\circ =-1\) \( \cos \ 270<>^\circ =0\)
\( \text\ 270<>^\circ =\frac\Rightarrow \text\ 270<>^\circ \) — не существует
\( \text\ 270<>^\circ =\frac=0\) \( \sin \ 360<>^\circ =0\) \( \cos \ 360<>^\circ =1\) \( \text\ 360<>^\circ =\frac=0\)
\( \text\ 360<>^\circ =\frac\Rightarrow \text\ 2\pi \) — не существует
\( \sin \ 450<>^\circ =\sin \ \left( 360<>^\circ +90<>^\circ \right)=\sin \ 90<>^\circ =1\) \( \cos \ 450<>^\circ =\cos \ \left( 360<>^\circ +90<>^\circ \right)=\cos \ 90<>^\circ =0\)
\( \text\ 450<>^\circ =\text\ \left( 360<>^\circ +90<>^\circ \right)=\text\ 90<>^\circ =\frac\Rightarrow \text\ 450<>^\circ \) — не существует
\( \text\ 450<>^\circ =\text\left( 360<>^\circ +90<>^\circ \right)=\text\ 90<>^\circ =\frac=0\).
Таким образом, мы можем составить следующую табличку:
![]()
Нет необходимости помнить все эти значения!
Достаточно помнить соответствие координат точек на единичной окружности и значений тригонометрических функций:
А вот значения тригонометрических функций углов в \( 30<>^\circ =\frac<\pi >,\ 45<>^\circ =\frac<\pi >\) и \( 30<>^\circ =\frac<\pi >,\ 45<>^\circ =\frac<\pi >\), приведённых ниже в таблице, необходимо запомнить:
![]()
Не надо пугаться, сейчас покажем один из примеров довольно простого запоминания соответствующих значений:
Синусом (sin) называют один из показателей угла, характеризующий отношение лучей, его образующих. Помимо него, в тригонометрии применяется также косинус (cos) , тангенс (tg) и котангенс (ctg) . Он обладает своими уникальными чертами характеристиками, которые и будут рассмотрены в этой статье.
Определение

Рис. 1. Прямоугольный треугольник У этой фигуры мы видим три угла, каждый со своим значением. Также каждый из них имеет свой показатель (sinx) , представляющий собой соотношение определенных сторон, например: \( \sin\gamma=\frac ba \) Таким образом, в случае если треугольник прямоугольный, синусом называют отношение противолежащего катета к гипотенузе.
Свойства и их формульное выражение
При работе с синусами используются различные их свойства. Проще всего распределить их по группам: Основное тождество :
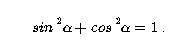
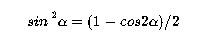
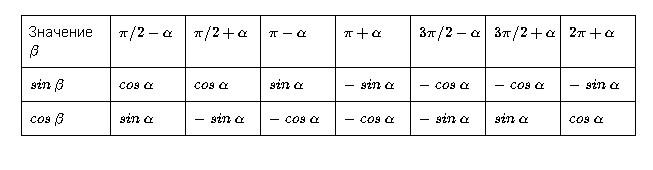
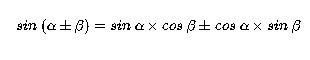
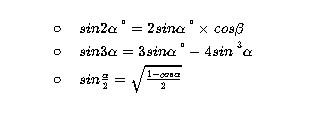
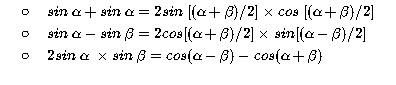
На тригонометрическом круге (рис.2) синус вычисляется по оси y. Соответственно - косинус по оси x, а тангенс и котангенс находятся через соотношение синуса и косинуса, по соответствующим формулам (о них подробнее рассказано в отдельных статьях).
Синус острого угла α (sin α) – это отношение противолежащего катета (a) к гипотенузе (c) в прямоугольном треугольнике.

График синуса
Функция синуса пишется как y = sin (x) . График называется синусоидой и в общем виде выглядит следующим образом:

Синусоида – это периодическая функция с периодом .
Свойства синуса
Ниже в табличном виде представлены основные свойства синуса с формулами:
| Свойство | Формула |
| Симметричность | sin (-α) = -sin α " data-order math">sin (-α) = -sin α "> |
| Симметричность | sin (90°- α) = cos α " data-order math">sin (90°- α) = cos α "> |
| Пифагорейская тригонометрическая идентичность | sin 2 α + cos 2 α = 1 " data-order math">sin 2 α + cos 2 α = 1 "> |
| sin α = cos α tg α " data-order math">sin α = cos α tg α "> | |
| sin α = 1 / csc α " data-order math">sin α = 1 / csc α "> | |
| Синус двойного угла | sin 2α = 2 sin α cos α " data-order math">sin 2α = 2 sin α cos α "> |
| Синус суммы углов | sin (α+β) = sin α cos β + cos α sin β " data-order math">sin (α+β) = sin α cos β + cos α sin β "> |
| Синус разности углов | sin (α-β) = sin α cos β - cos α sin β " data-order math">sin (α-β) = sin α cos β - cos α sin β "> |
| Сумма синусов | |
| Разность синусов | |
| Произведение синусов | |
| Произведение синуса и косинуса | |
| Закон синуса | a / sin α = b / sin β = c / sin γ " data-order math">a / sin α = b / sin β = c / sin γ "> |
| Производная синуса | sin' x = cos x " data-order math">sin' x = cos x "> |
| Интеграл синуса | ∫ sin x dx = -cos x + C " data-order math">∫ sin x dx = -cos x + C "> |
| Формула Эйлера | sin x = (e ix - e -ix ) / 2i " data-order math">sin x = (e ix - e -ix ) / 2i "> |
Обратная к синусу функция
Если синус угла у равняется х ( sin y = x ), значит арксинус x равен у :
Читайте также:





