Что такое пространство эйлера кратко

Обновлено: 03.07.2024

В математикаособенно в алгебраическая топология, то Класс Эйлера это характеристический класс из ориентированный, настоящий векторные пучки. Как и другие характеристические классы, он измеряет, насколько "скручено" векторное расслоение. В случае касательный пучок гладкой многообразие, оно обобщает классическое понятие Эйлерова характеристика. Он назван в честь Леонард Эйлер из-за этого.

Содержание

Формальное определение

В Класс Эйлера е(E) является изображением ты под состав этих карт.

Характеристики

Класс Эйлера удовлетворяет этим свойствам, которые являются аксиомами характеристического класса:

Функциональность: Если F → Y < displaystyle F to Y>- другое ориентированное действительное векторное расслоение и ж : Y → Икс < displaystyle f двоеточие от Y до X>непрерывна и покрывается сохраняющим ориентацию отображением F → E < displaystyle F to E>, тогда е ( F ) = ж ∗ ( е ( E ) ) < Displaystyle е (F) = е ^ (е (E))> . Особенно, е ( ж ∗ ( E ) ) = ж ∗ ( е ( E ) ) < Displaystyle е (е ^ (Е)) = е ^ (е (Е))> .
Уитниформула суммы: Если F → Икс < displaystyle F to X>является еще одним ориентированным вещественным векторным расслоением, то класс Эйлера их прямая сумма дан кем-то е ( E ⊕ F ) = е ( E ) ⌣ е ( F ) .
Нормализация: Если E < displaystyle E>имеет секцию нигде-ноль, тогда е ( E ) = 0 < Displaystyle е (Е) = 0>.
Ориентация: Если E ¯ < displaystyle < overline >> является E < displaystyle E>с противоположной ориентацией, то е ( E ¯ ) = − е ( E ) < Displaystyle е (< overline >) = - е (E)> .

Исчезающее геометрическое место общего сечения

Самопересечение

Связь с другими инвариантами

В особом случае, когда комплект E речь идет о касательном расслоении компактного ориентированного р-мерного многообразия класс Эйлера является элементом верхних когомологий многообразия, который естественным образом отождествляется с целыми числами, вычисляя классы когомологий на фундаментальный класс гомологии. При таком отождествлении класс Эйлера касательного расслоения равен эйлеровой характеристике многообразия. На языке характеристические числа, эйлерова характеристика - характеристическое число, соответствующее классу Эйлера.

Модифицирование на 2 вызывает карту

Любое сложное векторное расслоение E сложного ранга d можно рассматривать как ориентированное действительное векторное расслоение E реального ранга 2d. Класс Эйлера E задается классом Черна наивысшей размерности е ( E ) = c d ( E ) ∈ ЧАС 2 d ( Икс ) < Displaystyle е (Е) = c_ (E) в H ^ (X)>

Квадраты наверх Понтрягина класс

Нестабильность

Интуитивно это можно увидеть в том, что класс Эйлера - это класс, степень которого зависит от размерности расслоения (или многообразия, если касательное расслоение): класс Эйлера является элементом ЧАС d ( Икс ) < displaystyle H ^ (X)> куда d < displaystyle d>- размерность связки, в то время как другие классы имеют фиксированную размерность (например, первый класс Штифеля-Уитни является элементом ЧАС 1 ( Икс ) < displaystyle H ^ (X)> ).

Примеры

Сферы

Эйлерова характеристика п-сфера S п является:

Таким образом, не существует ненулевого сечения касательного пучка четных сфер (это известно как Теорема о волосатом шарике). В частности, касательное расслоение четной сферы нетривиально, т. Е. S 2 п < displaystyle S ^ > это не параллелизируемое многообразие, и не может допустить Группа Ли структура.

Для нечетных сфер S 2п−1 ⊂ р 2п , нигде не исчезающий участок задается

что показывает, что класс Эйлера обращается в нуль; это просто п копии обычного раздела по кругу.

Поскольку касательное расслоение сферы стабильно тривиально, но не тривиально, все остальные характеристические классы обращаются в нуль на нем, а класс Эйлера является единственным обычным классом когомологий, который обнаруживает нетривиальность касательного расслоения сфер: для доказательства дальнейших результатов один должен использовать вторичные когомологические операции или же K-теория.

Эйлерова характеристика или характеристика Эйлера — Пуанкаре — характеристика топологического пространства. Эйлерова характеристика пространства обычно обозначается .

Содержание

Определения

Для конечного клеточного комплекса (в частности для конечного симплициального комплекса) эйлерова характеристика может быть определена как знакопеременная сумма

Эйлерова характеристика произвольного топологического пространства может быть определена через числа Беттикак знакопеременная сумма:

Последнее определение обобщает предыдущее и обобщается на другие гомологии с произвольными коэффициентами.

Свойства

Эйлерова характеристика является гомотопическим инвариантом; то есть сохраняется при гомотопической эквивалентности топологических пространств.

В частности, эйлерова характеристика есть топологический инвариант.

Эйлерова характеристика полиэдров

Эйлерова характеристика двумерных топологических полиэдров может быть посчитана по формуле: +\hbox" width="" height="" />
где Г, Р и В суть числа граней, рёбер и вершин соответственно. В частности, для выпуклого многогранника верна формула Эйлера: +\hbox=\chi(S^2)=2." width="" height="" />

Теорема Гаусса — Бонне

Для компактного двумерного ориентированного риманова многообразия (поверхности) без границы существует формула Гаусса — Бонне, связывающая эйлерову характеристику с гауссовой кривизной многообразия:

$\int\limits_S K\;d\sigma = 2\pi\chi(S),$

где — элемент площади поверхности .

$2\pi$

Существует обобщение формулы Гаусса-Бонне для двумерного многообразия с краем.
Существует обобщение формулы Гаусса — Бонне на чётномерное римановых многообразий многообразия известная, как Теорема Гаусса — Бонне — Черна или Обобщённая формула Гаусса — Бонне.
Существует также дискретный аналог теоремы Гаусса — Бонне, гласящий, что Эйлерова характеристика равна сумме дефектов полиэдра, делённой на . [1]

Существует комбинаторные аналоги формулы Гаусса — Бонне.

Ориентированные и неориентированные поверхности

Величина эйлеровой характеристики

Название	Вид	Эйлерова характеристика
Отрезок		1
Окружность		0
Круг		1
сфера		2
Тор (произведение двух окружностей)		0
Двойной тор		−2
Тройной тор		−4
Проективная поверхность		1
Лист Мёбиуса		0
Бутылка Клейна		0
Две сферы(несвязные)		2 + 2 = 4
Три сферы		2 + 2 + 2 = 6

История

В 1752 году Эйлер [2] опубликовал формулу, связывающую между собой количество граней трёхмерного многогранника. В оригинальной работе формула приводится в виде

где S — количество вершин, H — количество граней, A — количество рёбер.

Ранее эта формула встречается в рукописях Р. Декарта, опубликованных в XVIII в.

В 1899 году Пуанкаре [3] обобщил эту формулу на случай N-мерного многогранника:

$\sum_<i=0> ^^i A_i =1+^,$

где — количество i-мерных граней N-мерного многогранника.

Если формально считать сам многогранник своей собственной единственной гранью размерности N, формулу можно записать в более простом виде:

$\sum_<i=0> ^^i A_i =1.$

Примечания

↑Practical Polygonal Mesh Modeling with Discrete Gaussian-Bonnet Theorem
↑L. EulerDemonstratio nonnullarum insignium proprietatum, quibus solida hedris planis inclusa sunt praedita. Novi Commentarii Academiae Scientiarum Petropolitanae 4:140–160, 1758. Представлено Санкт-Петербургской Академии 6 апреля1752 года. Opera Omnia 1(26): 94–108.
- Перевод на английский язык: Leonhard EulerProof of Some Notable Properties with wich Solids Enclosed by Plane Faces are Endowed. (Translated by Christopher Francese and David Richeson)
↑ H. Poincaré, Sur la généralisation d'un théorème d'Euler relatif aux polyèdres, Compt. Rend. Acad. Sci., 117 (1893), 144-145; Oeuvres, Vol. XI, 6-7.

Литература

Долбилин Н.Три теоремы о выпуклых многогранниках // Квант. — 2001. — № 5. — С. 7-12.
Лакатос И.Доказательства и опровержения. Как доказываются теоремы / Пер. И. Н. Веселовского. — М .: Наука, 1967.
Шашкин Ю. А.Эйлерова характеристика. — М .: Наука, 1984. — Т. 58. — (Популярные лекции по математике).

См. также

Проставив сноски, внести более точные указания на источники.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Эйлерова характеристика" в других словарях:

Эйлерова характеристика — многогранника, число αo α1 +α2, где αo число вершин, α1 число рёбер и α2 число граней многогранника. Если многогранник выпуклый или гомеоморфен (см. Гомеоморфизм) выпуклому, то его Э. х. равна двум (теорема Л. Эйлера, 1758, известная ещё… … Большая советская энциклопедия

ЭЙЛЕРОВА ХАРАКТЕРИСТИКА — конечного клеточного комплекса К целое число где число k мерных клеток комплекса. Названа в честь Л. Эйлера (L. Enler), к рый доказал в 1758, что число вершин В, ребер Р и граней Г. выпуклого многогранника связаны формулой В Р+Г=2. В неявном виде … Математическая энциклопедия

Характеристика Эйлера — В алгебраической топологии, эйлерова характеристика есть топологический инвариант (и даже гомотопический инвариант) определённый на большом классе топологических пространств. Обычно эйлерова характеристика пространства X обозначается χ(X).… … Википедия

МНОГОГРАННИК — часть пространства, ограниченная совокупностью конечного числа плоских многоугольников (см. ГЕОМЕТРИЯ), соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого… … Энциклопедия Кольера

ТОПОЛОГИЯ — в широком смысле область математики, изучающая топологич. свойства разл. матем. и физ. объектов. Интуитивно, к топологич. относятся качественные, устойчивые свойства, не меняющиеся при деформациях. Матем. формализация идеи о топологич. свойствах… … Физическая энциклопедия

Глоссарий общей топологии — Эта страница глоссарий. См. также основную статью: Общая топология В этом глоссарии приведены определения основных терминов, используемых в общей топологии. Курсивом выделены ссылки внутри глос … Википедия

Круги Эйлера (другое название — диаграммы Венна) — это геометрическая схема, которую можно применять для наглядного отображения отношений между множествами. Диаграммы разработал известный математик и механик, чьим именем и назван метод. Учёный считал, что его подход облегчает размышления человека.

Множества в математике

Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:

конечное, например, множество стран;
бесконечное — множество звёзд во вселенной;
пустое — множество острых углов в прямоугольнике.

Группа элементов, составляющая множество, входящее в другое, более обширное множество называется подмножеством. Такое отношение получается между множеством действительных чисел и входящим в его состав подмножеством натуральных чисел.

дополнение ¯A в калькуляторе имеет вид A';
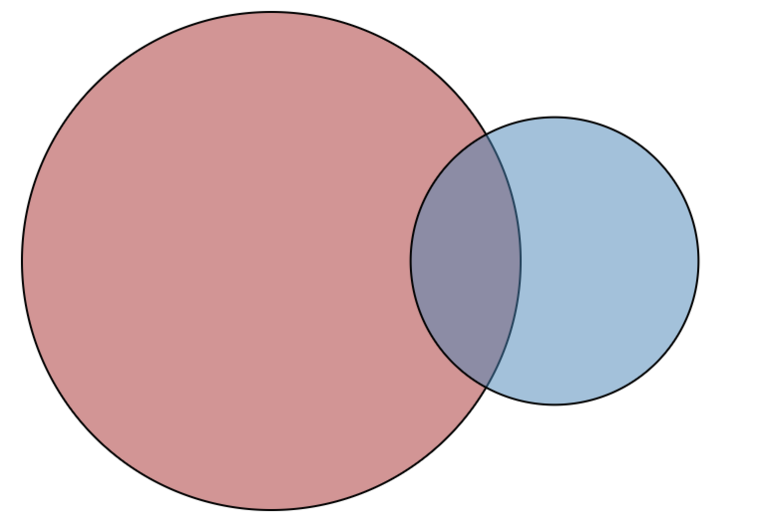
пересечение A∩B представлено как A intersection B;
объединение А⋃B обозначено A union B;
симметрическая разность A∆B — symmetric difference of A and B;
Относительное дополнение A\B — A\B.

Калькулятор выдаёт результат и подробное решение с правильным порядком операций при подстановке конкретных множеств.

Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.

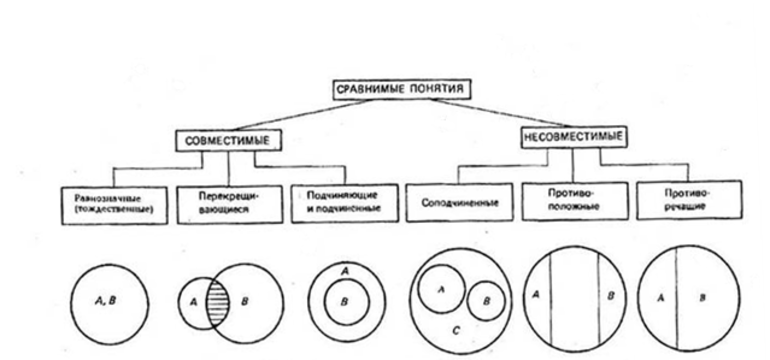
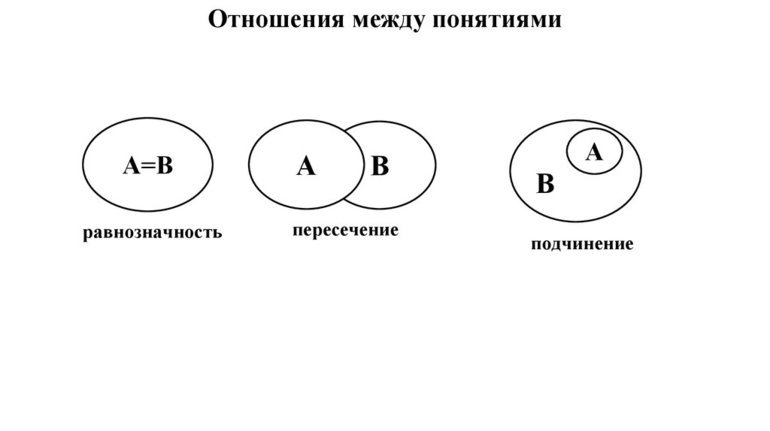
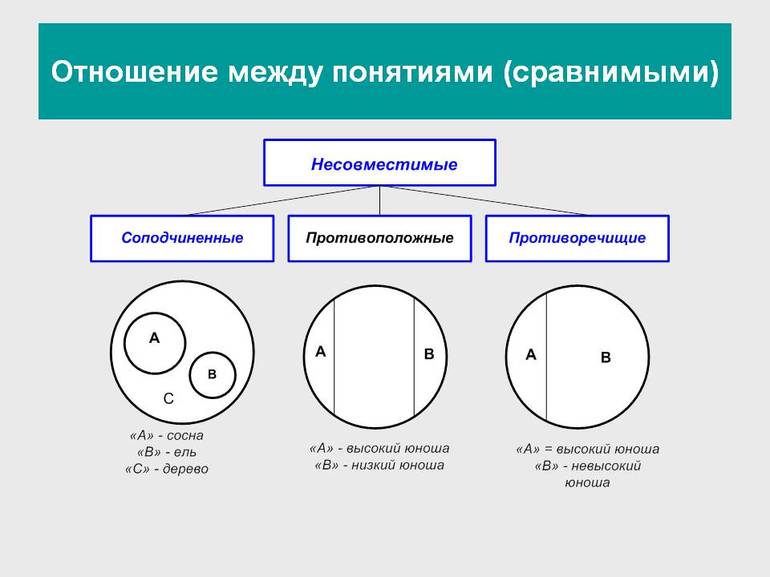
Отношения между понятиями

Рисунок 1

Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:

равнозначные (тождественные);
перекрещивающиеся;
подчиняющие и подчинённые.

Несовместимыми называют понятия, не имеющие общих элементов:

соподчинённые;
противоположные;
противоречащие.

Решение задач, примеры

Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.

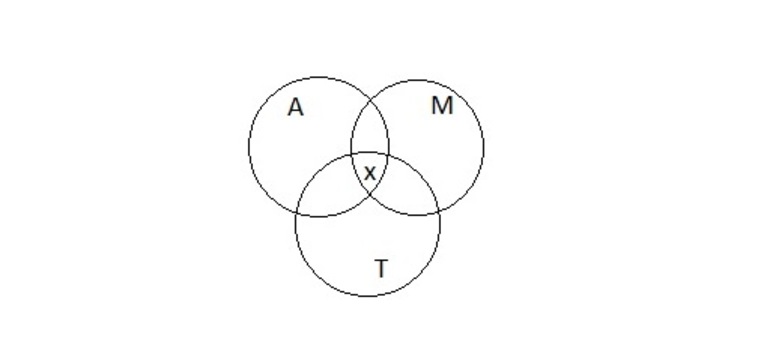
Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?

Рисунок 2

Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.

Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…

Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…

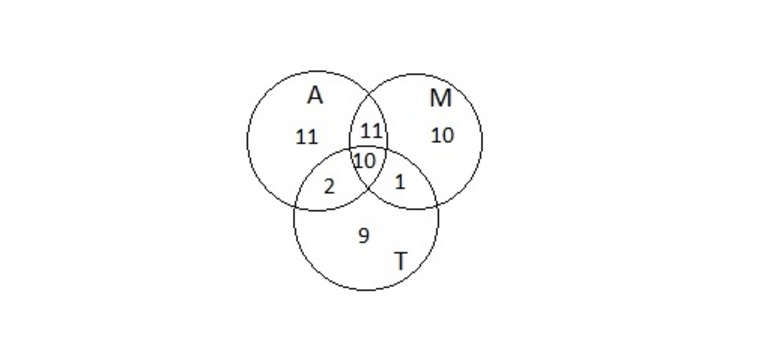
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).

54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.

Рисунок 3

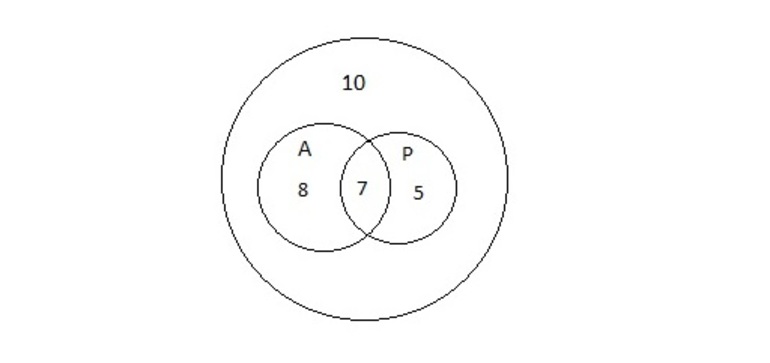
Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?

Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.

Рисунок 4

Соединим теперь основания высот A₁ и C₁ отрезком. И докажем, что треугольник C₁BA₁ подобен треугольнику ABC. Ну, действительно. У них есть общий угол B. Кроме того, если рассмотреть прямоугольный треугольник CC₁B, то косинус угла B в нём равен отношению прилежащего катета BC₁ к гипотенузе BC: " width="115" height="42" />
. С другой стороны, из прямоугольного треугольника ABA₁ мы получаем, что косинус того же самого угла B равен отношению прилежащего катета BA₁ к гипотенузе BA: " width="115" height="42" />
:

$\dfrac<BC_1> Ну и теперь мы видим, что общий угол B образован в наших треугольниках пропорциональными сторонами: = \dfrac$
. Значит, треугольники C₁BA₁ и ABC подобны. Причём их коэффициент подобия равен .

$\angle GA_1B = \angle GC_1B = 90^<\circ> Обратим теперь внимание на то, что$
. Это означает, что сумма противоположных углов четырёхугольника GC₁BA₁ равна 180 градусам. Значит, вокруг него можно описать окружность:

При этом отрезок BG будет являться диаметром этой окружности, поскольку на него опирается вписанный угол BA₁G, который равен 90 градусов.

Проведём теперь серединные перпендикуляры к сторонам AB и AC. Они пересекутся в точке O, которая, как хорошо известно, является центром описанной около треугольника ABC окружности. То есть треугольник AOC будет равнобедренным, причём его боковые стороны по длине будут равны радиусу описанной окружности:

$\cos B = \dfrac<r> То есть мы получили, что вокруг подобных треугольников BC1A1 и ABC описаны окружности. Но коэффициент их подобия равен косинусу угла B. Но в подобных треугольниках одинаковым образом относятся все элементы, в том числе и радиусы описанных окружностей, поэтому$
.

Проведём теперь высоту OD в треугольнике AOC. Обратим внимание, что угол B является вписанным и опирается на дугу AC. Но на эту же дугу опирается и центральный угол AOC, который поэтому должен быть вдвое больше угла B. Но высота OD делит этот угол ровно пополам, так как она является одновременно и биссектрисой, проведённой к основанию равнобедренного треугольника. Значит, ∠B = ∠DOC:

$\cos B = \dfrac<OD> Но тогда косинус угла B мы можем расписать, используя треугольник DOC. В нём этот косинус равен отношению прилежащего катета OD к гипотенузе OC, которая равна радиусу описанной окружности R. И этот же косинус, как мы выяснили, равен отношению r к R: = \dfrac$
. Из последнего равенства получаем, что или иначе .

Проведём теперь отрезок BD, который будет являться медианой. Проведём также прямую через точки O и G. То есть через эти две точки проходит прямая, что, конечно, не удивительно, ведь мы знаем, что через две точки можно провести прямую, притом только одну. Эта прямая пересекает медиану BD в некоторой точке M:

Как вы думаете, что это за точка? Уже догадались? А может быть уже знали и раньше? Если нет, то настало время удивляться! Посмотрите на треугольник OMD. Он подобен треугольнику MGB по двум углам: вертикальным и накрест лежащим при параллельных прямых. И мы даже знаем коэффициент подобия этих треугольников. Он равен 1:2. А значит, все стороны этих треугольников относятся как 1:2, в том числе и стороны DM и MB.

И что же у нас получилось? А получилось то, что точка M делит медиану BD в отношении 2:1, считая от вершины. А значит, точка M – это точка пересечения медиан треугольника или, как её по-другому называют, цетроид треугольника.

Таким образом мы доказали, что ортоцентр треугольника, центр описанной около него окружности и центроид этого треугольника лежат на одной прямой. Эта прямая и называется прямой Эйлера!

Анимация прямой Эйлера

Факт существования прямой Эйлера насколько удивителен, что даже не всегда укладывается в голове. Специально для вас я подготовил поясняющую анимацию. Посмотрите её в видео на моём Youtube-канале.

Вне зависимости от типа треугольника, как угодно можно над ним издеваться, но эти три точки всегда будут лежать на одной прямой. Возможны, правда, случаи, когда эти точки совпадают. Например, для правильного треугольника все они сливаются в одну точку. Но если мы имеем дело не с этим тривиальным случаем, то все эти точки лежат на одной прямой. Прямой Эйлера.

И у этой прямой очень много других интересных свойств. Пишите в комментариях, стоит ли написать на эту тему отдельную статью. Успехов!

Проблемы в определении

Фигуры, не являющиеся многогранниками

Правильный

Первые шаги к теореме Эйлера для многогранников

Полиэдральная формула

Систематическое исследование этих фигур началось сравнительно рано в истории математики. Леонард Эйлер был первым, кто заметил, что для выпуклых трехмерных многогранников справедлива формула, связывающая число их вершин, граней и ребер.

Она выглядит так:

где V – число многогранных вершин, F — число ребер многогранников, а E — число граней.

Леонард Эйлер – швейцарский математик, который считается одним из величайших и производительных ученых всех времен. Он большую часть жизни был слеп, но потеря зрения послужила ему поводом стать еще более продуктивным. Существует несколько формул, названных в его честь, и ту, которую мы только что рассмотрели, иногда называют формулой многогранников Эйлера.

Есть одно уточнение. Формула Эйлера, однако, работает только для многогранников, которые следуют определенным правилам. Они заключаются в том, что форма не должна иметь никаких отверстий. И недопустимо, чтобы она пересекала саму себя. Многогранник также не может состоять из двух частей, соединенных вместе, например, двух кубов с одной вершиной. Эйлер упомянул о результате своего исследования в письме к Христиану Гольдбаху в 1750 году. Позднее он опубликовал две работы, в которых описал, как попытался найти доказательство своего нового открытия. На самом деле существуют формы, которые дают другой ответ на V + F - E. Ответ на сумму F + V - E = Х называется эйлеровой характеристикой. У нее есть еще один аспект. Некоторые формы могут даже иметь характеристику Эйлера, которая является отрицательной

Теория графов

Доказательства формулы Эйлера

Эйлер сначала сформулировал полиэдральную формулу как теорему о многогранниках. Сегодня ее часто трактуют в более общем контексте связанных графов. Например, как структуры, состоящие из точек и отрезков линий, соединяющих их, которые находятся в одной части. Огюстен Луи Коши был первым человеком, который нашел эту важную связь. Она и послужила доказательством теоремы Эйлера. Он, в сущности, заметил, что граф выпуклого многогранника (или то, что сегодня называется таковым) топологически гомеоморфен сфере, имеет плоский связный граф. Что это такое? Плоский граф — это тот, который был нарисован в плоскости таким образом, что его ребра встречаются или же пересекаются только в вершине. В этом и была найдена связь теоремы Эйлера и графов.

Одним из признаков важности результата является то, что Дэвид Эпштейн смог собрать семнадцать различных доказательств. Существует много вариантов обоснования полиэдральной формулы Эйлера. В некотором смысле наиболее очевидными доказательствами являются методы, использующие математическую индукцию. Результат можно доказать, проводя ее по числу либо ребер, граней либо вершин графа.

Доказательство Радемахера и Теплица

Иордановая кривая. Теорема

Основной тезис, который прямо или косвенно используется при доказательстве формулы многогранников теоремы Эйлера для графов, зависит от Иордановой кривой. Эта идея связана с обобщением. Она гласит, что любая простая замкнутая кривая делит плоскость на три множества: точки на ней, внутри и вне ее. Поскольку интерес к многогранной формуле Эйлера развился в девятнадцатом веке, было сделано много попыток обобщить ее. Это исследование заложило основу для развития алгебраической топологии и связало ее с алгеброй и теорией чисел.

Группа Мебиуса

Диаграмма Эйлера

Ученый совершил еще одно открытие, которое используется до сих пор. Это так называемая диаграмма Эйлера — графическое изображение, состоящее из кругов, обычно используемое для иллюстрации отношений между множествами или группами. Диаграммы обычно включают цвета, которые смешиваются в областях, где круги перекрываются. Множества же изображаются именно кругами или овалами, хотя для них также могут быть использовать другие фигуры. Включение представлено перекрытием эллипсов, называемых эйлеровыми кругами.

Они представляют множества и подмножества. Исключение составляют неперекрывающиеся круги. Диаграммы Эйлера тесно связаны с другим графическим изображением. Их часто путают. Это графическое изображение называется диаграммами Венна. В зависимости от рассматриваемых множеств обе версии могут выглядят одинаково. Однако на диаграммах Венна перекрывающиеся круги необязательно указывают на общность между множествами, а только на возможную логическую связь, если их метки не находятся в пересекающемся круге. Оба варианта были приняты для преподавания теории множеств в рамках нового математического движения 1960-х годов.

Теоремы Ферма и Эйлера

Эйлер оставил заметный след в математической науке. Алгебраическая теория чисел обогатилась теоремой, названной в его честь. Она также является следствием другого важного открытия. Это так называемая общеалгебраическая теорема Лагранжа. Имя Эйлера также связано с малой теоремой Ферма. В ней говорится, что если p — простое число и a — целое число, не делящееся на p, то:

а p-1 - 1 делится на p.

Иногда это же открытие носит другое название, чаще всего встречающееся в иностранной литературе. Звучит оно как "рождественская теорема Ферма". Все дело в том, что открытие стало известно благодаря письму ученого, отправленного в канун 25 декабря 1640 года. Но само утверждение встречалось и раньше. Его использовал другой ученый по имени Альбер Жирар. Ферма лишь пытался доказать его теорию. Автор намекает в другом своем письме на то, что его вдохновил метод бесконечного спуска. Но никаких доказательств он не привел. Позже к этому же методу обратиться и Эйдер. А после него - множество других известных ученых, в том числе Лагранж, Гаусс и Минкоский.

Особенности тождеств

Малая теорема Ферма называется также частным случаем теоремы из теории чисел, принадлежащей Эйлеру. В этой теории функция тождества Эйлера подсчитывает положительные целые числа до заданного целого числа n. Они взаимно просты по отношению к n. Теорема Эйлера в теории чисел записывается с использованием греческой буквы φ и выглядит как φ (n). Ее можно более формально определить как число целых чисел k в диапазоне 1 ≤ k ≤ n, для которого наибольший общий делитель gcd (n, k) равен 1. Запись φ (n) также может называться фи-функцией Эйлера. Целые числа k этой формы иногда называются тотативными. В основе теории чисел функция тождества Эйлера является мультипликативной, означающей, что если два числа m и n взаимно просты, то φ(mn) = φ(m)φ(n). Она также играет ключевую роль в определении системы шифрования RSA.

Читайте также: