Что такое ориентированный граф кратко
Обновлено: 30.06.2024
Ориентированные графы или, для краткости, орграфы используются для моделирования ситуаций, в которых есть отношение частичного порядка между объектами. Возникающие при этом схемы служат для изображения схем информационных потоков, сетевого планирования и планирования заданий.
Основные положения
Ориентированный граф или орграф представляет собой пару G = (V, Е), где V — конечное множество вершин, а Е — отношение на V. Графическое изображение графа состоит из множества помеченных вершин с ориентированными ребрами (называемых дугами), соединяющими пары вершин. Совокупность всех дуг образует множество Е.
Дугу, соединяющую пару (и, v) вершин и и v орграфа G, будем обозначать через uv. В простом орграфе отсутствуют петли и кратные дуги. Следовательно, для любой пары вершин и и v в орграфе найдется не более одной дуги uv из вершины u и v, и не более одной дуги vu из v в и. Если uv — дуга орграфа, то и называют антецедентом v.
На рис. 8.1 приведен пример простого орграфа с множеством вершин V = и множеством дуг Е = .
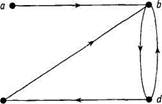
c
Рисунок 8.1. Пример орграфа
Матрицей смежности данного графа служит (несимметричная) матрица
| а | b | с | d | |
| a | Л | и | л | Л |
| b | Л | л | л | и |
| с | Л | и | л | л |
| d | л | и | и | л |
(вершины а, с и d здесь — антецеденты 6).
Путем длины к в орграфе называют последовательность различных вершин vо, v1,…, vk, каждая пара vi-1vi которой образует дугу( i = 1. k).
Контуром в орграфе G принято называть последовательность вершин vo, v1, . vk, образующую путь, в которой первая вершина vо совпадает с последней vk , а других повторяющихся вершин в ней нет. Орграф G называют бесконтурным, если в нем нет контуров.
Пример 8.1.Для получения степени магистра биологии студенту университета, в частности, необходимо прослушать восемь курсов, которые некоторым образом зависят друг от друга. Эта зависимость представлена в табл. 8.1. Изобразите систему ПЕРТ, иллюстрирующую приоритетную структуру курсов.
| Предварительные курсы | ||
| (А) | Биотехнология | В |
| (В) | Начальный курс биотехнологии | С |
| (С) | Цитология | н |
| (D) | Структура ДНК | с |
| (Е) | Этимология | D, G |
| (F) | Диетология | Е |
| (G) | Генная инженерия | С |
| (Н) | Биология человека | Никаких требований |
Решение.Система ПЕРТ (см. рис. 8.2) — это просто орграф, представляющий данную приоритетную структуру. Вершины орграфа в данном случае — восемь курсов. Для краткости ссылок мы обозначим курсы буквами латинского алфавита от А до Н. Дуги орграфа отражают представленные в таблице требования, необходимые для усвоения данного курса.
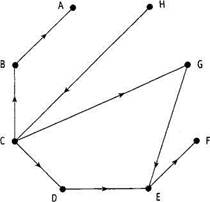
Рисунок 8.2. Система ПЕРТ: приоритетная структура курсов
Предположим, что студент из примера 8.1 намерен определить порядок, в котором ему следует изучать предметы, учитывая их, зависимость друг от друга. Он может сделать это с помощью алгоритма топологической сортировки. Алгоритм создает последовательность согласованных меток для вершин бесконтурного орграфа таким образом, что если 1, 2, 3, . п — метки вершин и uv — дуга орграфа, идущая от вершины и с меткой iк вершине v с меткой j, то i - (v) и d + (v)
d + (a)=1, d + (b)=0, d + (c)=1, d + (d)=2.
d - (a)=1, d - (b)=2, d - (c)=1, d - (d)=0.
Теорема(лемма о рукопожатиях):Сумма степеней всех вершин обыкновенного графа равна удвоенному количеству ребер, Сумма полустепеней исхода и захода орграфа равна удвоенному количеству ребер.
Ориентированные графы
Ориентированные графы или, для краткости, орграфы используются для моделирования ситуаций, в которых есть отношение частичного порядка между объектами. Возникающие при этом схемы служат для изображения схем информационных потоков, сетевого планирования и планирования заданий.

Основные положения
Ориентированный граф или орграф представляет собой пару G = (V, Е), где V — конечное множество вершин, а Е — отношение на V. Графическое изображение графа состоит из множества помеченных вершин с ориентированными ребрами (называемых дугами), соединяющими пары вершин. Совокупность всех дуг образует множество Е.
Дугу, соединяющую пару (и, v) вершин и и v орграфа G, будем обозначать через uv. В простом орграфе отсутствуют петли и кратные дуги. Следовательно, для любой пары вершин и и v в орграфе найдется не более одной дуги uv из вершины u и v, и не более одной дуги vu из v в и. Если uv — дуга орграфа, то и называют антецедентом v.
На рис. 8.1 приведен пример простого орграфа с множеством вершин V = и множеством дуг Е = .

c
Рисунок 8.1. Пример орграфа
Матрицей смежности данного графа служит (несимметричная) матрица
| а | b | с | d | |
| a | Л | и | л | Л |
| b | Л | л | л | и |
| с | Л | и | л | л |
| d | л | и | и | л |
(вершины а, с и d здесь — антецеденты 6).
Путем длины к в орграфе называют последовательность различных вершин vо, v1,…, vk, каждая пара vi-1vi которой образует дугу( i = 1. k).
Контуром в орграфе G принято называть последовательность вершин vo, v1, . vk, образующую путь, в которой первая вершина vо совпадает с последней vk , а других повторяющихся вершин в ней нет. Орграф G называют бесконтурным, если в нем нет контуров.
Пример 8.1.Для получения степени магистра биологии студенту университета, в частности, необходимо прослушать восемь курсов, которые некоторым образом зависят друг от друга. Эта зависимость представлена в табл. 8.1. Изобразите систему ПЕРТ, иллюстрирующую приоритетную структуру курсов.
| Предварительные курсы | ||
| (А) | Биотехнология | В |
| (В) | Начальный курс биотехнологии | С |
| (С) | Цитология | н |
| (D) | Структура ДНК | с |
| (Е) | Этимология | D, G |
| (F) | Диетология | Е |
| (G) | Генная инженерия | С |
| (Н) | Биология человека | Никаких требований |
Решение.Система ПЕРТ (см. рис. 8.2) — это просто орграф, представляющий данную приоритетную структуру. Вершины орграфа в данном случае — восемь курсов. Для краткости ссылок мы обозначим курсы буквами латинского алфавита от А до Н. Дуги орграфа отражают представленные в таблице требования, необходимые для усвоения данного курса.

Рисунок 8.2. Система ПЕРТ: приоритетная структура курсов
Предположим, что студент из примера 8.1 намерен определить порядок, в котором ему следует изучать предметы, учитывая их, зависимость друг от друга. Он может сделать это с помощью алгоритма топологической сортировки. Алгоритм создает последовательность согласованных меток для вершин бесконтурного орграфа таким образом, что если 1, 2, 3, . п — метки вершин и uv — дуга орграфа, идущая от вершины и с меткой iк вершине v с меткой j, то i - (v) и d + (v)
d + (a)=1, d + (b)=0, d + (c)=1, d + (d)=2.
d - (a)=1, d - (b)=2, d - (c)=1, d - (d)=0.
Теорема(лемма о рукопожатиях):Сумма степеней всех вершин обыкновенного графа равна удвоенному количеству ребер, Сумма полустепеней исхода и захода орграфа равна удвоенному количеству ребер.

В этой статье мы познакомимся с основными терминами и определениями Теории графов. Каждый термин схематично показан на картинках.
Граф - это топологичекая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.
Например, граф на рисунке состоит из 8 вершин и 8 рёбер.

Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними - за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.
В этой статье мы познакомимся с основными терминами и определениями теории графов. На курсе “Алгоритмы и Структуры данных” в компании Отус “Теория графов” изучается в самом объёмном модуле из 6 вебинаров, где мы изучаем десяток самых популярных алгоритмов.
Вершина - точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения.
Ребро - неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге - не имеет значения; однако рёбра может быть присвоен “вес”, что позволит говорить о “нагруженном графе” и решать задачи оптимизации.
Инцидентность - вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин “инцидентность” применим только к вершине и ребру.
Смежность вершин - две вершины называются смежными, если они инцидентны одному ребру.
Смежность рёбер - два ребра называются смежными, если они инцедентны одной вершине.
Говоря проще - две вершины смежные, если они соединены ребром, два ребра смежные - если они соединены вершиной.

Петля - ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине.
Псевдограф - граф с петлями. С такими графами не очень удобно работать, потому что переходя по петле мы остаёмся в той же самой вершине, поэтому у него есть своё название.

Кратные рёбра - рёбра, имеющие одинаковые концевые вершины, по другому их называют ещё параллельными.
Мультиграф - граф с кратными рёбрами.
Псевдомультиграф - граф с петлями и кратными рёбрами.

Степень вершины - это количество рёбер, инцидентных указанной вершине. По-другому - количество рёбер, исходящих из вершины. Петля увеливает степень вершины на 2.
Изолированная вершина - вершина с нулевой степенью.
Висячая вершина - вершина со степенью 1.

Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы получим подграф исходного графа.

Идея подграфов используется во многих алгоритмах, например, сначала создаётся подграф их всех вершин без рёбер, а потом дополняется выбранными рёбрами.
Полный граф - это граф, в котором каждые две вершины соединены одним ребром.

Сколько рёбер в полном графе? Это известная задача о рукопожатиях: собралось N человек (вершин) и каждый с каждым обменялся рукопожатием (ребро), сколько всего было рукопожатий? Вычисляется как сумма чисел от 1 до N - каждый новый участник должен пожать руку всем присутствующим. Сумму нужно разделить на два, так как в этом случае каждое рукопожатие посчитается дважды: N * (N - 1) / 2.
Регулярный граф - граф, в котором степени всех вершин одинаковые.

Двудольный граф - если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера.

Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется “планарным графом” или “плоским графом”.

Если это невозможно сделать, то граф называется “непланарным”.
Минимальные непланарные графы - это полный граф К5 из 5 вершин и полный двудольный граф К3,3 из 3+3 вершин (известная задача о 3 соседях и 3 колодцах). Если какой-либо граф в качестве подграфа содержит К5 или К3,3, то он является непланарным.

Путь или Маршрут - это последовательность смежных рёбер. Обычно путь задаётся перечислением вершин, по которым он пролегает.
Длина пути - количество рёбер в пути.
Цепь - маршрут без повторяющихся рёбер.
Простая цепь - цепь без повторяющихся вершин.

Цикл или Контур - цепь, в котором последняя вершина совпадает с первой.
Длина цикла - количество рёбер в цикле.
Самый короткий цикл - это петля.

Цикл Эйлера - цикл, проходящий по каждому ребру ровно один раз. Эйлер доказал, что такой цикл существует тогда, и только тогда, когда все вершины в связанном графе имеют чётную степень.

Цикл Гамильтона - цикл, проходящий через все вершины графа по одному разу. Другими словами - это простой цикл, в который входят все вершины графа.

Взвешенный граф - граф, в котором у каждого ребра и/или каждой вершины есть “вес” - некоторое число, которое может обозначать длину пути, его стоимость и т. п. Для взвешенного графа составляются различные алгоритмы оптимизации, например поиск кратчайшего пути.

Пока ещё не придуман алгоритм, который за полиномиальное время нашёл бы кратчайший цикл Гамильтона в полном нагруженном графе, однако есть несколько приближённых алгоритмов, которые за приемлимое время находят если не кратчайший, то очень короткий цикл, эти алгоритмы мы также рассматриваем на курсе Отуса - “Алгоритмы и структуры данных”.
Связный граф - граф, в котором существует путь между любыми двумия вершинами.
Дерево - связный граф без циклов.
Между любыми двумя вершинами дерева существует единственный путь.
Деревья часто используются для организации иерархической структуры данных, например, при создании двоичных деревьев поиска или кучи, в этом случае одну вершину дерева называют корнем.

Лес - граф, в котором несколько деревьев.

Ориентированный граф или Орграф - граф, котором рёбра имеют направления.
Дуга - направленные рёбра в ориентированном графе.

Полустепень захода вершины - количество дуг, заходящих в эту вершину.
Исток - вершина с нулевой полустепенью захода.
Полустепень исхода вершины - количество дуг, исходящих из этой вершины
Сток - вершина с нулевой полустепенью исхода.

Компонента связности - множество таких вершин графа, что между любыми двумя вершинами существует маршрут.

Компонента сильной связности - максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам.
Компонента слабой связности - максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам без учёта направления (по дугам можно двигаться в любом направлении).

Мост - ребро, при удалении которого, количество связанных компонент графа увеличивается.

Это только основные термины и определения теории графов, которые мы рассматриваем на первом вебинаре модуля “Теория графов”. Цель статьи - дать наглядное и понятное представление об этих терминах, для чего и были нарисованы эти картинки.
В графе ребро, концы которого совпадают, то есть [math]e=(v, v)[/math] , называется петлей (англ. loop).
Два ребра, имеющие общую концевую вершину, то есть [math]e_1=(v, u_1)[/math] и [math]e_2=(v, u_2)[/math] , называются смежными (англ. adjacent).
Если имеется ребро [math] (v, u) \in E [/math] , то говорят:
- [math] v [/math] — предок (англ. direct predecessor) [math] u [/math] .
- [math] u [/math] и [math] v [/math] — смежные.
- Вершина [math] u [/math] инцидентна ребру [math] (v, u) [/math] .
- Вершина [math] v [/math] инцидентна ребру [math] (v, u) [/math] .
Инцидентность (англ. incidence) — понятие, используемое только в отношении ребра и вершины. Две вершины или два ребра не могут быть инцидентны.
Граф с [math] p [/math] вершинами и [math] q [/math] рёбрами называют [math] (p, q) [/math] -графом. [math] (1, 0) [/math] -граф называют тривиальным.
Заметим, что по определению ориентированного графа, данному выше, любые две вершины [math]u,~v[/math] нельзя соединить более чем одним ребром [math](u, v)[/math] . Поэтому часто используют другое определение.
Данное определение разрешает соединять вершины более чем одним ребром. Такие рёбра называются кратными (иначе — параллельные, англ. multi-edge, parallel edge). Граф с кратными рёбрами принято называть мультиграфом (англ. multigraph). Если в мультиграфе присутствуют петли, то такой граф называют псевдографом (англ. pseudograph).
Граф — абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин.
В теории графов вершиной называется фундаментальная единица, образующая графы — неориентированный граф состоит из множества вершин и множества рёбер (неупорядоченных пар вершин), в то время как ориентированный граф состоит из множества вершин и множества дуг (упорядоченных пар вершин). На рисунках, представляющих граф, вершина обычно обозначается кружком с меткой, ребро — линией, дуга — стрелкой, соединяющей вершины.
Дерево — это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.
Связный граф — граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует как минимум один путь. Другими словами, нет изолированной вершины ( такой, которая не имеет соответствующих ей рёбер (называется "ребра, инцидентные вершине 1" (или 2) ).
Упоминания в литературе
Элементов множество. Возьмем пример, что связи между элементами системы являются направленными по линии воздействия одного элемента на другой. Представим систему в виде ориентированного графа (рисунок 2), где элементы представлены вершинами, а связи между ними – дугами. Воздействующий элемент является предшествующим, и начало стрелки связи, идущей от него (начало дуги), – выходом этого элемента. Элемент, испытывающий воздействие, является последующим, и конец стрелки связи, поступающей в него (конец дуги), есть вход этого элемента. Частными случаями являются: взаимодействие двух элементов (b и d на рисунке 2 а), когда соединяющие две смежные вершины дуги образуют контур, и самосопряжение элемента, когда его выход возвращается на вход, т.е. образуется петля (с на рисунке 2а). У замкнутой системы элементы взаимодействуют лишь внутри системы. Для варианта незамкнутой системы такая однозначная идентификация невозможна. Здесь элементы могут быть отнесены либо к системе, либо к среде, т.е. к другой системе: вершина b на рисунке 2a стала входом х2' и выходом y2' на рисунке 2 в. В реальной действительности нет абсолютно обособленных систем, но пользоваться этой абстракцией удобно. Число связей, их направление и разветвленность являются структурными характеристиками системы.
Связанные понятия (продолжение)
Двудо́льный граф или бигра́ф — это математический термин теории графов, обозначающий граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.
Орграф называется сильно связным (англ. strongly connected), если любые две его вершины сильно связны. Две вершины s и t любого графа сильно связны, если существует ориентированный путь из s в t и ориентированный путь из t в s.
Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице).
Визуализация или отображение графов, как ответвление теории графов, относящееся к топологии и геометрии — двумерное представление графа. В основном, это графическое представление укладки графа на плоскость (как правило, допускается пересечение рёбер), направленное, обычно, на удобное отображение некоторых свойств графа, или моделируемого объекта.
Остовное дерево графа состоит из минимального подмножества рёбер графа, таких, что из любой вершины графа можно попасть в любую другую вершину, двигаясь по этим рёбрам.
Ориентация неориентированного графа — это назначение направлений каждому ребру, что превращает исходный граф в ориентированный граф.
Плана́рный граф — граф, который может быть изображён на плоскости без пересечения рёбер. Иначе говоря, граф планарен, если он изоморфен некоторому плоскому графу, то есть графу, изображённому на плоскости так, что его вершины — это точки плоскости, а рёбра — непересекающиеся кривые на ней. Области, на которые граф разбивает плоскость, называются его гранями. Неограниченная часть плоскости — тоже грань, так называемая внешняя грань.
В теории графов паросочетание или независимое множество рёбер в графе — это набор попарно несмежных рёбер.
Раскраска графов находит применение и во многих практических областях, а не только в теоретических задачах. Помимо классических типов проблем, различные ограничения могут также быть наложены на граф, на способ присвоения цветов или на сами цвета. Этот метод, например, используется в популярной головоломке Судоку. В этой области всё ещё ведутся активные исследования.
Гамильто́нов граф — математический объект теории графов. Представляет собой граф (набор точек и соединяющих их линий), который содержит гамильтонов цикл. При этом гамильтоновым циклом является такой цикл (замкнутый путь), который проходит через каждую вершину данного графа ровно по одному разу.
Мост — ребро в теории графов, удаление которого увеличивает число компонент связности. Такие рёбра также известны как разрезающие рёбра, разрезающие дуги или перешейки. Эквивалентное определение — ребро является мостом в том и только в том случае, если оно не содержится ни в одном цикле.
Полный двудольный граф (биклика) — специальный вид двудольного графа, у которого любая вершина первой доли соединена со всеми вершинами второй доли вершин.
Зада́ча о незави́симом мно́жестве относится к классу NP-полных задач в области теории графов. Эквивалентна задаче о клике.
Порождённый подграф графа — это другой граф, образованный из подмножества вершин графа вместе со всеми рёбрами, соединяющими пары вершин из этого подмножества.
В теории графов графом-циклом называется граф, состоящий из единственного цикла, или, другими словами, некоторого числа вершин, соединённых замкнутой цепью. Граф-цикл с n вершинами обозначают как Cn. Число вершин в Cn равно числу рёбер и каждая вершина имеет степень 2, то есть любая вершина инцидентна ровно двум рёбрам.
Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь.
В теории графов рёберным графом L(G) неориентированного графа G называется граф L(G), представляющий соседство рёбер графа G.
Кликой неориентированного графа называется подмножество его вершин, любые две из которых соединены ребром. Клики являются одной из основных концепций теории графов и используются во многих других математических задачах и построениях с графами. Клики изучаются также в информатике — задача определения, существует ли клика данного размера в графе (Задача о клике) является NP-полной. Несмотря на эту трудность, изучаются многие алгоритмы для поиска клик.
Эйлеров цикл — эйлеров путь, являющийся циклом, то есть замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.
В теории графов графом пересечений называется граф, представляющий схему пересечений семейства множеств. Любой граф можно представить как граф пересечений, но некоторые важные специальные классы можно определить посредством типов множеств, используемых для представления в виде пересечений множеств.
В теории графов графом гиперкуба Qn называется регулярный граф с 2n вершинами, 2n−1n рёбрами и n рёбрами, сходящимися в одной вершине. Его можно получить как одномерный скелет геометрического гиперкуба. Например, Q3 — это граф, образованный 8 вершинами и 12 рёбрами трёхмерного куба. Граф можно получить другим образом, отталкиваясь от семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества.
Полиэдральный граф — неориентированный граф, образованный из вершин и рёбер выпуклого многогранника, или, в контексте теории графов — вершинно 3-связный планарный граф.
В теории графов стягивание ребра — это операция, которая удаляет ребро из графа, а до этого связанные ребром вершины сливаются в одну вершину. Стягивание ребра является фундаментальной операцией в теории о минорах графов. Отождествление вершин — другая форма этой операции с более слабыми ограничениями.
Автоморфизм графа есть отображение множества вершин на себя, сохраняющее смежность. Множество таких автоморфизмов образует вершинную группу графа или просто группу графа. Группа подстановок на множестве ребер называется реберной группой графа, которая тесно связана с вершинной.
Поиск в ширину (англ. breadth-first search, BFS) — метод обхода графа и поиска пути в графе. Поиск в ширину является одним из неинформированных алгоритмов поиска.
Хромати́ческое число́ гра́фа G — минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Обычно обозначается χ(G).
В теории графов граф сравнимости — это неориентированный граф, в котором пары элементов соединены ребром, если эти элементы сравнимы в некотором частичном порядке. Графы сравнимости также называют транзитивно-ориентируемыми графами, частично упорядочиваемыми графами и графами вложенности.
Окрестность часто обозначается как NG(v) или (если известно, о каком графе идёт речь) N(v). То же самое обозначение окрестности может использоваться для ссылки на множество смежных вершин, а не на соответствующий порождённый подграф. Окрестность, описанная выше, не включает саму вершину v и об этой окрестности говорят как об открытой окрестности вершины v. Можно определить окрестность, включающую v. В этом случае окрестность называется закрытой и обозначается как NG. Если не указано явно, окрестность.
Кубический граф — граф, в котором все вершины имеют степень три. Другими словами, кубический граф является 3-регулярным. Кубические графы называются также тривалентными.
Задача поиска изоморфного подграфа — это вычислительная задача, в которой входом являются два графа G и H и нужно определить, не содержит ли G подграф, изоморфный графу H.
Кососимметрический граф — это ориентированный граф, который изоморфен своему собственному транспонированному графу, графу, образованному путём обращения всех дуг, с изоморфизмом, который является инволюцией без неподвижных точек. Кососимметрические графы идентичны двойным покрытиям двунаправленных графов.
Гомоморфизм графов — это отображение между двумя графами, не нарушающее структуру. Более конкретно, это отображение между набором вершин двух графов, которое отображает смежные вершины в смежные.
Сильно регулярный граф является дистанционно-регулярным с диаметром 2, но только в том случае, когда μ не равно нулю.
В теории графов неориентированный граф H называется минором графа G, если H может быть образован из G удалением рёбер и вершин и стягиванием рёбер.
Характеризация запрещёнными графами — это метод описания семейства графов или гиперграфов путём указания подструктур, которым запрещено появляться внутри любого графа в семействе.
В теории графов глубина дерева связного неориентированного графа G — это числовой инвариант G, минимальная высота дерева Тремо для суперграфа графа G. Этот инвариант и близкие понятия встречаются под различными именами в литературе, включая число ранжирования вершин, упорядоченное хроматическое число и минимальная высота исключения дерева. Понятие близко также к таким понятиям, как циклический ранг ориентированных графов и высота итерации языка регулярных языков ; . Интуитивно, если древесная ширина.
Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном взвешенном неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.
В теории графов псевдолес — это неориентированный граф , в котором любая связная компонента имеет максимум один цикл. То есть это система вершин и рёбер, соединяющих пары вершин, такая, что никакие два цикла не имеют общих вершин и не могут быть связаны путём. Псевдодерево — это связный псевдолес.
Число очередей графа — это инвариант графа, определённый аналогично стэковому числу (толщине книги) и использующий упорядочение FIFO (первый вошёл, первый вышел, очередь) вместо упорядочения LIFO (последним вошёл, первым вышел, стэк).
Задача о гамильтоновом пути и задача о гамильтоновом цикле — это задачи определения, существует ли гамильтонов путь (путь в неориентированном или ориентированном графе, который проходит все вершины графа ровно один раз) или гамильтонов цикл в заданном графе (ориентированном или неориентированном). Обе задачи NP-полны.
Симметричный граф (или транзитивный относительно дуг граф) — граф G, для любых двух пар смежных вершин которого u1—v1 и u2—v2 имеется автоморфизм.
Читайте также:

