Что такое мнимая единица кратко

Обновлено: 02.07.2024

Введение мнимой единицы позволяет расширить поле вещественных чисел до поля комплексных чисел. Одной из причин введения мнимой единицы является то, что не каждое полиномиальное уравнение f ( x ) = 0 с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x 2 + 1 = 0 +1=0> не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — об этом говорит основная теорема алгебры. Существуют и другие области, в которых комплексные числа приносят большую пользу.

Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: при наличии трёх вещественных корней для получения двух из них формула Кардано требовала извлечения квадратных корней из отрицательных чисел.

числа i и −i являются одновременно противоположными и обратными: последнее верно потому, что произведение этих чисел равно 1 ;
i и −iкомплексно сопряжены, так что их сумма (ноль) и произведение (единица) вещественны одновременно (свойства сопряжённых чисел).

Ранее мы с вами разобрали пару крайне важных, в нашем мире, чисел: число Эйлера и число ПИ . Сегодня мы с вами узнаем еще об одном интересном и важном числе.

Мнимая единица , по сути, его нельзя назвать числом в привычном нам понимании. Это число не вещественное, а комплексное. Давайте пойдем по порядку.

Сперва история

Первые заметки о нем были обнаружены в записях Джероламо Кардано - итальянский математик живший в 16 веке. Он ввел его, когда решал кубические уравнения . Позже, когда ученые обнаружили эти записи, они начали производить с ним различные действия.

Основной вклад в развитие этой теории вложил ранее знакомый нам Леонард Эйлер . Тогда родился комплексный анализ, а позже и теория функций комплексного переменного ( ТФКП ). Леонард распространил основные функции в комплексную плоскость. Было сформулировано множество принципов, алгебраические действия не отличались от привычного вещественного анализа, но было сделано одно существенное допущение: в этой теории есть число, квадрат которого равен отрицательному числу . И это мнимая единица. Обозначается она как i , и такое название она получила благодаря все тому же Эйлеру (в некоторых других науках, таких как электротехника , встречается обозначение j , так как буква i занята для обозначения тока).

По определению мнимая единица - это число, квадрат которого равен -1 (i^2 = -1). Давайте попробуем поразмыслить, что это значит.

Для нахождения площади квадрата , мы возводим длину стороны этого квадрата в квадрат. То есть, мнимая единица - это сторона квадрата, у которого отрицательная площадь . Да, на реальности мы такого не встретим, именно по этому она называется мнимой. Но какой от нее тогда толк? Об этом немного позже.

Немного введу в курс дела

В комплексном анализе числовая прямая расширяется до комплексной плоскости , где осью абсцисс представлена вещественная прямая, а осью ординат - мнимая. Существует несколько способов записи комплексного числа: в виде пары чисел, в алгебраической форме, тригонометрической и вытекающей отсюда показательной.

Самая красивая формула математики

Я хочу показать вам одну красивую формулу в математике, а для этого необходимо немного разобраться в комплексном анализе.

Давайте взглянем на комплексную плоскость поподробнее. На ней числа отмечаются точками, и каждой соответствует своя координата .

Но так же возможно векторное представление , где начало вектора лежит в начале координат, а конец на точке.

Благодаря этому возможно ввести показательное представление . Где число перед экспонентой показывает длину вектора, а угол в показателе равен углу между вещественной осью и этим вектором.

А теперь давайте рассмотрим следующий случай: пусть длина вектора равняется 1 , а угол будет равен пи, то есть, пол оборота. Так мы попадем в точку -1 на вещественной оси.

То есть e^(i*pi) = -1. Переписав ее в несколько другом виде можно получить следующее выражение:

Это так называемая формула Эйлера (на самом деле это лишь частный случай этой формулы). И вся ее красота состоит в том, что она содержит в себе все знаменитые константы и числа .

Важность этого числа

Так же, современная аэродинамика не обходится без ТФКП , где функции Жуковского могут давать необходимые профили крыла.

И это еще не все. Во многих отраслях так или иначе могут присутствовать элементы этой теории, поэтому ее важность нельзя отрицать.

Если данная статья была вам интересна, то не забывайте ставить пальцы вверх, я постарался написать для вас наиболее понятно. Так же подписывайтесь на канал, если еще не сделали этого! До скорых встреч и всего доброго! :)

Мнимая единица — в основном комплексное число, квадрат которого равняется отрицательной единице: .

Число называется мнимой единицей.

Мнимая единица не относится к привычному нам множеству действительных чисел, а используется для расширения этого множества.

Мнимая единица — это число, у которого квадрат равняется минус единице. То есть i — это одно из решений уравнения:

или .

И тогда его вторым решением уравнения будет , что можно проверить подстановкой.

Комплексная плоскость. Все точки на плоскости соответствуют комплексному числу. Координаты a и b соответствуют действительной и мнимой части комплексного числа.

Примеры расчетов с мнимой единицей.

Интересно то, что все многочлены имеют корни, если брать в расчет мнимую единицу, если точнее, количество корней равняется степени многочлена, с точностью до кратности корней.

Степени мнимой единицы .

Степени i повторяются циклично:

Это можно записать для любой степени таким образом:

где n — всякое целое число.

Отсюда: , где mod 4 это остаток от деления на 4.

Число оказывается вещественным числом:

Корни из мнимой единицы .

В поле комплексных чисел корень n-ой степени имеет n решений. На комплексной плоскости корни из мнимой единицы расположены в вершинах правильного n-угольника, который вписан в окружность единичного радиуса.

Это следует из формулы Муавра и того, что мнимую единицу можно представить в тригонометрическом виде:

В частности, и

Кроме того, корни из мнимой единицы можно представить в показательном виде:

Человеку не сведущим в математике и физике рассуждения о мнимой единице представляется полным бредом. Например, квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Отсюда ясно, что квадратные корни из отрицательных чисел не могут находиться среди возможных действительных чисел. Следовательно, нам не остается ничего другого, как признать их невозможными числами.

Все учились в школе и изучали математику, для кого-то это был скучный предмет, а для кого-то математика в списке любимых школьных предметов. В начальной школе изучали арифметику (азы математики), в основной школе алгебру и геометрию (что-то уже по круче), и в старшей школе начала математического анализа и во всех этих школьных периодах разговор начинался с понятия числа. Натуральные числа это: 1,2,3,4…, точнее, множество натуральных чисел ( они нужны при счёте, всегда применяем в повседневной жизни). Потом познакомились с множеством целых чисел: -4,-3,-2,-1,0,1,2,3… Здесь нужно заметить, что множество целых чисел содержит в себе ряд натуральных чисел, нуль и отрицательные числа.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел. Это было сделано китайскими математиками во II веке до н. э. Отрицательные числа не так просты. Представьте, сколько будет 3 – 4? Как можно отнять 4 барана от 3? Отрицательные числа рассматривались как полная чушь. Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число Е и много еще чего, не понимал отрицательные числа так же хорошо, как

Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Эти числа называли иррациональными, объединяя все предыдущие множества (натурально, целое, рациональное и иррациональное), получили множество - действительных чисел.

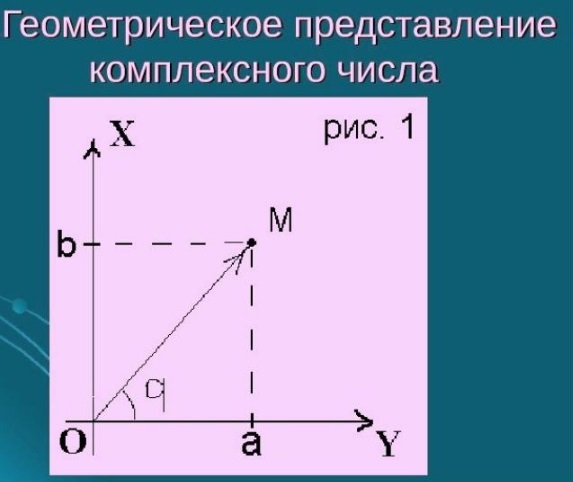
Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс означает связь, сочетание, совокупность понятий, предметов, явлений образующих единое целое. В конце XVIII века, в начале XIX века было получено геометрическое истолкование комплексных чисел. Датчанин К. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изобразить комплексное число z = a + b × i точкой m (a, b) на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой M, а вектором, идущим в эту точку из начала координат. Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения. В дальнейшем Леонард Эйлер (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) получил знаменитую формулу, и открыл комплексным числам дорогу в самые различные области математики и ее приложений.

Комплексные числа – расширили понятие числа. В 1843 году ирландский математик Уильям Гамильтон предложил четырехмерную систему комплексных чисел, которая стала первой гиперкомплексной системой, названную кватернионами. Теория кватернионов вскоре стала одним из источников дальнейшего развития математики и ее приложений.

Значение математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения.

Сейчас уже нельзя назвать такой области деятельности людей, где математика не играла бы существенной роли. Она стала незаменимым орудием во всех науках о природе, в технике, в обществоведении. Даже юристы и историки берут на своё вооружение математические методы. Инженер, не владеющий математическими методами, - это не инженер, а монтёр. Ничего нельзя сделать без математики: мост построить нельзя, плотину – нельзя, гидростанцию – нельзя. Сокращать объём преподавания математики в школах – преступление! Надо изучать её как можно в большем объёме, а главное – как можно основательнее.

Читайте также: