Простые числа в криптографии сообщение

Обновлено: 04.07.2024

Рис.2. Древнегреческий математик Евклид

Конечно, способ Эратосфена не смог удовлетворить ученых, и они пытались найти формулу простых чисел. На протяжении многих столетий это сделать не удавалось. В ряду простых чисел были найдены многие интересные закономерности, но поставленная задача оставалась без ответа. Над поиском максимально больших простых чисел в своё время бились Катальди, Декарт, Ферма, Мерсенн, Лейбниц, Эйлер и многие другие математики. В математике широко известен термин простые числа Мерсенна. Простые числа Мерсена являются простыми числами специального вида

где р — другое простое число.

До 1750 года было найдено всего 8 простых чисел Мерсенна: М2, М3, М5, М7, М13, М17, М19, М31. То, что М31 - простое число, доказал в 1750 году Л. Эйлер. В 1876 году французский математик Эдуард Люка установил, что число М127=170141183460469231731687303715884105727 - простое. В 1883 г. сельский священник Пермской губернии И.М.Первушин доказал, что число М61=2305843009213693951 является простым. Позднее было установлено, что числа М89 и М107 простые. 12 простых чисел Мерсена были вычислены с помощью только карандаша и бумаги, а для вычисления следующих уже использовались механические настольные счетные машины.

Масштабный проект по поиску простых чисел GIMPS был запущен в 1997 году, и ныне считается самым длительным непрерывным процессом распределённых вычислений в истории человечества: он продолжается уже почти 20 лет. Сейчас в пиковые моменты в GIMPS участвует 360.000 процессоров с суммарной производительностью 150 трлн операций в секунду. За время работы GIMPS участники этого проекта нашли 14 простых чисел Мерсенна. Последнее из них 274 207 281-1 было обнаружено 07 января 2016 года. Всего на данный момент известно 49 простых чисел Мерсена. В списке самых больших простых чисел, известных на сегодняшний день, десять первых мест занимают числа Мерсенна.

Поиск простых чисел — по крайней мере больших простых чисел — довольно сложная задача, потому что еще никому не удалось найти точную формулу или алгоритм, позволяющий генерировать любые простые числа.

Применение простых чисел в криптографии.

Актуальны ли простые числа сегодня? Еще как! Простые числа являются основой современной криптографии, так что большинство людей пользуются ими каждый день, даже не задумываясь об этом. Любой процесс аутентификации, например, регистрация телефона в сети, банковские платежи и прочее, требуют криптографических алгоритмов.

Алгоритм шифрования RSA

Алгоритм, представленный Гарднером, известен как RSA — буквенная аббревиатура от фамилий Rivest (Ривест), Shamir (Шамир) и Adleman (Адлеман). Это первое практическое применение придуманной Диффи системы шифрования с открытым ключом, которая повсеместно используется и по сей день. Надежность ее практически гарантирована, потому что процесс расшифровки является невероятно сложным, почти невозможным делом.

На сегодняшний день разложить числа, состоящие из тысячи и более цифр, за соизмеримое с человеческой жизнью время, способны только суперкомпьютеры! Именно с их помощью ученные находят все новые и новые, наибольшие из известных, простые числа.

Представим, что один человек, зашифровав важную информацию, установил на нее пароль (P) равный одному из простых делителей числа (А), сказав другому человеку, что число (А) содержит только два простых делителя и дав ему ключ для расшифровки – число (B), являющееся вторым делителем числа (А). Не трудно понять, что для расшифровки необходимо разделить А на B, чтобы получить пароль Р. Например в элементарном варианте А=111, ключ B=3 тогда пароль равен А/B=37.

Допустим, число А попало к злоумышленнику, и он знает условие о том, что А состоит из 2-х простых делителей. При условии, что А=111 злоумышленнику не составит особого труда даже в уме взломать пароль. Теперь представим ситуацию, когда число А состоит из 2 простых чисел, каждое из которых состоит из тысячи цифр… Если злоумышленник не знает ключа (одного из делителей), для факторизации числа А, состоящего из двух тысяч цифр, ему потребуется, как минимум, суперкомпьютер и большое количество времени его работы. Если попытаться попытается разложить произведение — даже при помощи самого быстрого суперкомпьютера — это не получится. Просто не существует такого алгоритма, который справился бы с этой задачей за время жизни Вселенной.

Для применения алгоритма RSA требуется построить открытый и секретный ключи следующим образом.

1. Выбрать два больших простых числа, p и q.

2. Найти их произведение n = p • q и значение ϕ =(р-1)-(q-1)

3. Выбрать число e (1 C = Т e mod n

(e, n) — открытый ключ,

Где применяют алгоритм RSA на практике? Криптосистема RSA используется в самых различных продуктах, на различных платформах и во многих отраслях. В настоящее время криптосистема RSA встраивается во многие коммерческие продукты, число которых постоянно увеличивается. Также ее используют операционные системы Microsoft, Apple, Sun и Novell. В аппаратном исполнении RSA алгоритм применяется в защищенных телефонах, на сетевых платах Ethernet, на смарт-картах, широко используется в криптографическом оборудовании. Кроме того, алгоритм входит в состав всех основных протоколов для защищенных коммуникаций Internet, в том числе S/MIME, SSL и S/WAN, а также используется во многих учреждениях, например, в правительственных службах, в большинстве корпораций, в государственных лабораториях и университетах. На осень 2000 года технологии с применением алгоритма RSA были лицензированы более чем 700 компаниями.

Технологию шифрования RSA BSAFE используют около 500 миллионов пользователей всего мира. Так как в большинстве случаев при этом используется алгоритм RSA, то его можно считать наиболее распространенной криптосистемой общего (public) ключа в мире и это количество имеет явную тенденцию к увеличению по мере роста Internet.

На начало 2001 года криптосистема RSA являлась наиболее широко используемой асимметричной криптосистемой (криптосистемой открытого (public) ключа) и зачастую называется стандартом де факто. Вне зависимости от официальных стандартов существование такого стандарта чрезвычайно важно для развития электронной коммерции и вообще экономики. Единая система открытого (public) ключа допускает обмен документами с электронно-цифровыми подписями между пользователями различных государств, использующими различное программное обеспечение на различных платформах; такая возможность насущно необходима для развития электронной коммерции. Распространение системы RSA дошло до такой степени, что ее учитывают при создании новых стандартов. При разработке стандартов цифровых подписей, в первую очередь в 1997 был разработан стандарт ANSI X9.30, поддерживающий Digital Signature Standard (стандарт Цифровой подписи). Годом позже был введен ANSI X9.31, в котором сделан акцент на цифровых подписях RSA, что отвечает фактически сложившейся ситуации, в частности, для финансовых учреждений.

Проведение анкетирования

Объясняем, почему простые числа важны в криптографии. Для этого мы рассмотрим конкретную криптосистему, а именно алгоритм RSA и сосредоточимся на его основных аспектах.

Свойства простых чисел

Каждое число можно разложить на простые множители. В некоторых случаях факторизация целых чисел представляет из себя сложный процесс. В первую очередь потому, что для больших чисел задача факторизации является вычислительно сложной. Подойдем к вопросу теоретически: для того чтобы найти все простые факторы (множители) числа n , нужно разделить данное число на все возможные множители вплоть до √n .

С другой стороны, вычислить значение гораздо легче, когда простые числа нам заранее известны:

x из простых чисел 1 и 2. Но сложно вычислить простые числа 1 и 2 из x ." data-src="https://media.proglib.io/posts/2022/01/19/2ed794022eaa0e480e954dd6fb23cca0.jpg" > Легко вычислить x из простых чисел 1 и 2. Но сложно вычислить простые числа 1 и 2 из x .

Криптографические системы

То есть, на практике реализация данного случая затруднена. Ведь, если мы хотим написать кому-то зашифрованное письмо, в наши планы не входит личная встреча с человеком для обмена секретными ключами.

Используем простые числа для шифрования

Теперь, когда у нас имеется четкое представление о двух различных системах шифрования, давайте рассмотрим, каким образом мы создадим открытый и закрытый ключ в случае асимметричного шифрования.

Для начала следует отметить, что мы не можем зашифровать текст напрямую, а должны сначала преобразовать его в число. Этот процесс называется подстановкой и происходит с помощью списка, в котором каждому символу присваивается число.

Затем мы соединяем каждое число, чтобы создать другое (назовем его m), которое мы потом зашифруем. Самым простым примером списка является присвоение каждой букве ее позиции в алфавите, например, A – 1, Б – 2 и т. д. Несмотря на то, что данный список позволяет использовать только крайне простые слова, его достаточно для понимания теории, лежащей в основе RSA .

Создаем ключ

Как было ранее сказано, некоторое большое число легко вычислить при условии, что простые числа уже известны. С другой стороны, очень трудно определить множители (факторы) известного нам большого числа. Чтобы создать два ключа – закрытый и открытый, – мы осуществляем следующий процесс:

Выберите два случайных, стохастически независимых и простых числа, p и q .
Вычислите их произведение: N = p * q
Далее вычислите φ-функцию: φ(N) = (p – 1) * (q – 1)
Выберите простое натуральное число e, которое меньше значения φ(N) и является кратным по отношению к нему.
Вычислите мультипликативную обратную величину k от e по модулю φ(N) , то есть: e * k + d * φ(N) = 1

И расшифруем его:

Из выражений выше следует, что мы можем инвертировать наше шифрование только если нам известна мультипликативная обратная k от e по модулю φ(N) . Эти данные возможно получить, если у нас есть:

Приватный (закрытый) ключ
Простые множители N

Практический пример

Пусть буква, которую мы хотим зашифровать – O . Преобразуем ее в число m=15 , так как это пятнадцатая буква латинского алфавита. Теперь мы выбираем случайные простые числа. Чтобы упростить задачу, выберем простые числа p = 13 и q = 17 .

Таким образом, функция: φ(N) = (p – 1) * (q – 1) = 192

Мы также выбираем число e , которое кратно φ(N) . Пусть это будет 29 .

Осталось вычислить обратное k от e . С помощью алгоритма Евклида мы узнаем, что оно равно 53 .

Таким образом, у нас есть открытый ключ N = p * q = 221 и закрытый ключ k = 53 .

Далее мы зашифруем наше число:

Теперь нам нужно наше обратное k , которое равно 53 :

Из данного материала вы узнали об алгоритме RSA (Rivest, Shamir и Aldeman – создатели алгоритма) и о том, как правильно его применять для шифрования данных.

Мы можем использовать другие, более объемные числа. Их невозможность разложения на простые множители поможет созданию безопасной и асимметричной криптографической системы.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

1 2 3 9 4 5 6 7 8 10

Справка о предмете исследования Просто́е число́ — это натуральное число, которое имеет ровно два различных натуральных делителя: единицу и самого себя. Все остальные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. Число 1 не относится ни к простым, ни к составным числам. Последовательность простых чисел начинается так: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, …

Более двух тысяч лет назад великий древнегреческий математик Евклид доказал, что ряд простых чисел бесконечен. Одной из самых больших загадок математики является расположение простых чисел в ряду всех натуральных чисел. Простые числа следуют одно за другим по закону, который еще не найден. Иногда два простых числа идут через одно (например, 17 и 19, 29 и 31), а иногда подряд идет миллион составных чисел. Сейчас ученые знают уже довольно много о том, сколько и какие простые числа содержатся среди натуральных чисел. Но остаётся ещё много неподтверждённых гипотез, несовершённых открытий в этой области исследований.

Для людей поиск простых чисел превратился в целенаправленный отбор отдельных представителей этого ряда. Один из рекордов поставил в своё время Эйлер, найдя простое число 231 − 1 = 2147483647. Наибольшим известным простым числом по состоянию на февраль 2011 года является 243112609 − 1. Оно содержит 12 978 189 десятичных цифр и является простым числом Мерсенна (M43112609). Его нашли 23 августа 2008 года на математическом факультете университета UCLA в рамках проекта по распределённому поиску простых чисел Мерсенна GIMPS. Назначение простых чисел

За нахождение простых чисел из более чем 100 000 000 и 1 000 000 000 десятичных цифр организация за свободу в интернете (EFF) назначила денежные призы соответственно в 150 000 и 250 000 долларов США. Ранее EFF уже присуждала призы за нахождение простых чисел из 1 000 000 и 10 000 000 десятичных цифр. Так зачем люди так настойчиво продолжают искать простые числа? Большие простые числа (порядка 10300) используются в криптографии с открытым ключом. Простые числа также используются в хеш-таблицах и для генерации псевдослучайных чисел

Криптография - наука о способах преобразования (шифрования) информации с целью ее защиты от незаконных пользователей (разработка шифров). Все используемые сегодня криптосистемы (с открытым ключом) опираются на алгоритмы разложения больших чисел на простые множители, работы с простыми числами. Таким образом, простые числа являются одной из неотъемлемых частей современных асимметричных криптосистем, то есть систем, использующих два ключа: открытый и секретный. Для того, чтобы криптосистема была стойкой к вскрытию, в ней необходимо использовать простые числа большой длины (и выше). Для того, чтобы использовать большие простые числа, их необходимо сначала построить.

Напомню, что математикам до сих пор не удавалось обнаружить какой-либо системы в характере распределения простых чисел. Так, считается, что в окрестности целого числа х среднее расстояние между последовательными простыми числами пропорционально логарифму х. Тем не менее, уже давно известны так называемые парные простые числа (простые числа-близнецы, разность между которыми равна 2: 11 и 13, 29 и 31, 59 и 61). Иногда они образуют целые скопления, например 101, 103, 107, 109 и 113. У математиков давно существовало подозрение, что такие скопления существуют и в области очень больших простых чисел, однако ни доказать, ни опровергнуть это утверждение до сих пор не удавалось.

Эратосфен придумал для поиска простых чисел следующий способ: Сначала вычеркивают все числа, делящиеся на 2 (исключая само число 2). Потом берут первое из оставшихся чисел (а именно 3). Ясно, что это число - простое. Вычеркивают все идущие после него числа, делящиеся на 3. Первым оставшимся числом будет 5. Вычеркивают все идущие после него числа, делящиеся на 5, и т.д. Числа, которые уцелеют после всех вычеркиваний, и являются простыми: 2, 3, 5, 7, 11, 13, …

В поисках истины Первый алгоритм поиска простых чисел, приходящий в голову, примерно таков. Каждое число из интервала от 1 до N проверить на "простоту" по определению: оно должно делиться только на 1 и себя. Подсчитаем сколько раз оно делится нацело и получим ответ: … For I:=1 to N do begin K:=0; For J:=1 to I do If I mod J = 0 then K:=K+1; If K=2 then Writeln(‘ ‘,I); end; …

Рассмотрим недостатки данного алгоритма: В Паскале по некоторым причинам результат компиляции Inc(K), работает быстрее, чем K:=K+1. Нет смысла делить I на все числа, большие, чем половина I - все равно нацело не разделится. Кроме того, подсчёт количества делений сам по себе не нужен: любое удачное деление нацело на число, не равное 1 и самому себе свидетельствует о том, что число не является простым. Но самый главный недостаток алгоритма – большое количество итераций (повторений) цикла, примерно n*(n/2).

Суть дальнейшего и главного улучшения алгоритма вычисления множества простых чисел заключается в следующем: нет необходимости производить деления на составные числа, так как каждое составное число есть произведение простых его составляющих. Постепенно такого рода рассуждения приводят к наиболее оптимальному алгоритму поиска простых чисел как в небольшом, так и достаточно большом интервале. Огромную роль играют ограничения, накладываемые на алгоритм поиска. Если имеется ограничение по времени (что очень вероятно), то алгоритм Эратосфена с заданием справляется очень хорошо, особенно для больших чисел. Если имеется очень узкое ограничение по занимаемой памяти компьютера (очень маловероятно), то простая проверка перебором - достаточно удобный способ.

C помощью множества Множество целых чисел не превышает значения 255. Если число не простое - исключаем его из множества. Перед работой присваиваем множеству диапазон чисел от 2 до N: Var M:set of byte; i,k,N:byte; begin readln(N); M:=[2..N]; k:=2; repeat for i:=k+1 to N do if (i in M) and (i mod k=0) then M:=M-[i]; inc(k); while (k N; for i:=2 to N do if i in M then write(' ',i); readln; end.

C помощью массива Лучше использовать массив с элементами логического типа. Будем считать, что на i-ом месте массива P стоит true (или 1) если число простое, иначе false (или 0). Перед работой массив нужно "проинициализировать" значениями true (или 1), т.е. считаем, что все числа простые (как при доказательстве от противного): Var P:array [2..65535] of boolean; i,k,N:word; begin readln(N); fillchar(P,N,1); k:=2; repeat for i:=k+1 to N do if P[i] and (i mod k=0) then P[i]:=false; inc(k); while (k N; for i:=2 to N do if P[i] then write(' ',i); readln; end.

C помощью строк Будем считать, что на i-ом месте строки S стоит '*' если число простое, иначе ' ' (пробел). Перед работой со строкой нужно ее "инициализировать" символами '*', т.е. считаем, что все числа простые (как при доказательстве от противного). Кроме этого нужно знать, что строка содержит не более 255 символов (как сделать еще больше? Создать массив символов - это другой способ): Var S:string[255]; i,k,N:byte; begin readln(N); fillchar(S,N,'*'); S[1]:=' '; k:=2; repeat for i:=k+1 to N do if (S[i]='*')and(i mod k=0) then S[i]:=' '; inc(k); while (k N; for i:=2 to N do if S[i]='*' then write(' ',i); readln; end.

Выясняем, как и откуда можно получить электронную подпись на примере криптосистемы RSA.

Содержание

Определения и обозначения

Описание криптосистемы RSA

Асимметричные криптографические системы

Шифрование и дешифрование

Электронная подпись документов

Введение

Наверняка вы сталкивались с таким понятием, как "электронная подпись". Если обратиться к федеральному закону, то можно найти следующее её определение:

Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2012, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.

Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.

Теорминимум

Сформируем небольшой словарик терминов, которые нам пригодятся далее:

Открытый текст – данные, подлежащие шифрованию или полученные в результате расшифрования

Шифртекст – данные, полученные в результате применения шифра к открытому тексту

Шифр – совокупность обратимых преобразований, зависящая от некоторого параметра (ключа)

Ключ – параметр шифра, определяющий выбор одного преобразования из совокупности.

Факторизация – процесс разложения числа на простые множители.

НОД – наибольший общий делитель.

Числа a и b называются взаимно простыми, если НОД этих чисел равен 1.

Функция Эйлера φ(n) – функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним.

Хочу отметить, что на данном этапе подразумевается, что вы знакомы с арифметическими операциями по модулю. Если нет, то здесь можно о них почитать.

Как оно устроено

Прежде, чем ~~окунуться в необъятный мир математики~~ рассмотреть, как именно устроена RSA, обратимся к тому, как работают

Асимметричные криптосистемы

Рассмотрим задачу сохранности содержимого посылки при передаче от отправителя к адресату. Вот картинка с многим полюбившимся Алисой и Бобом:

Теперь к математике

Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция я y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно. Аналогично, односторонней функцией с секретом называется функция y=f(x, k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.

Подобным свойством обладает операция возведения числа в степень по модулю:

Что есть что разобрались, теперь перейдём к конкретике, а именно – генерации ключей Боба. Давайте выберем число n такое, что:

где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид:

Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является вычислительно сложной задачей, ровно как и нахождение обратного элемента по модулю. Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).

Возвращаемся к генерации ключей. Выберем целое число e:

Для него вычислим число d:

Для отыскания числа, обратного по модулю, можно воспользоваться алгоритмом Евклида.

Мы завершили с этапом генерации ключей. Теперь Боб публикует свой открытый ключ (e, n), прячет закрытый d, а мы переходим к Алисе.

Шифруем, дешифруем.

Здесь за с обозначен шифртекст, который Алиса будет должна передать Бобу. Отметим также, что c ∈ [1, n − 1], как и m. Расшифруем шифртекст, возведя его в степень закрытого ключа Боба d:

А теперь ответим на вопрос, почему m ≡ m′ . Ниже я приведу доказательство данного утверждения, но если оно (доказательство) вам не сильно интересно, то можете его пропустить и просто поверить, что это так.

Здесь нам понадобится теорема Эйлера:

Также полезной будет китайская теорема об остатках:

Ещё раз напишем две ключевые формулы шифрования и расшифрования соответственно:

Если Алиса получила, что m ≡ m′, то подпись считается правильной.

Дочитавших до этого места хочу поздравить с получением первой цифровой подписи "на бумаге"!

Подпись документов

Рассмотренный алгоритм получения подписи изящен и прост в осознании, однако операция возведения в степень несколько "мешается". Наша текущая задача – подписать объёмный документ. Чтобы сэкономить время, мы не будем подписывать содержимое документа, а прибегнем к помощи хэш-функций (если вы не знаете, что такое хэш-функция, рекомендую почитать википедию). Скажу лишь то, что выходная последовательность хэш-функции имеет небольшую (по сравнению с размером ключей) длину, а также по имеющемуся хэшу нельзя однозначно восстановить исходные данные.

На картинках наглядно показано, в какой момент мы используем хэширование. Создание подписи:

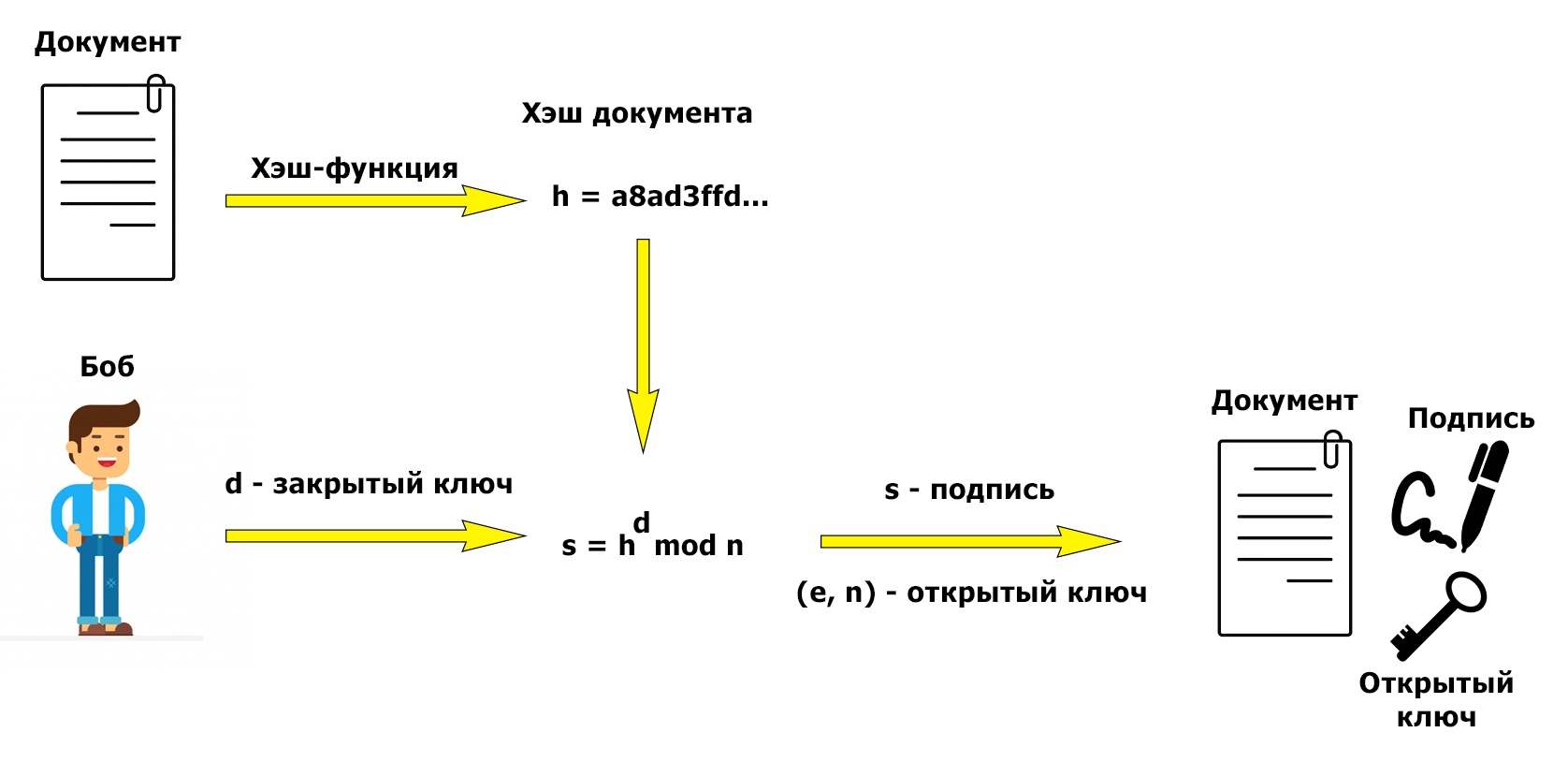
В качестве хэш-функции можно использовать SHA-256, как это сделано, например, в PGP. По теме практического создания электронной подписи с использованием PGP на хабре уже написана статья, поэтому на этом месте имеет смысл поставить точку и перейти к заключению.

Заключение

Вот мы и прошли все стадии создания электронной подписи, начиная с простой модульной арифметики и заканчивая, собственно, получением подписи. Обладая этими знаниями, вы можете попробовать перевести их на ваш любимый язык программирования и написать свою защищенную аську, например. В том, как именно их применить, вас ограничит только ваше воображение.

Отмечу, что другие существующие алгоритмы создания ЭП основаны на схожих принципах, поэтому надеюсь, что после прочтения этой статьи вам будет проще разобраться в них. "Следующей по сложности" я обозначу криптосистему Эль-Гамаля, но о ней уже не в этом посте.

Спасибо за внимание!

Источники

Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone

Криптографические методы защиты информации: учеб. пособие / С. М. Владимиров, Э. М. Габидулин, А. И. Колыбельников, А. С. Кшевецкий; под ред. А. В. Уривского. – М.: МФТИ, 2016

Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006.

NIST Special Publication 800-57 Part 3 Revision 1

Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. – СПб.: БХВ-Петербург, 2010. - Учебное пособие

Читайте также: