Центральная симметрия сообщение 11 класс
Обновлено: 30.06.2024
Центральная симметрия — это свойство фигуры, у которой есть некоторые точки В и В1, соединяющие отрезок и совпадающие в пространстве относительно фиксированного элемента — центральной точки С.
Симметричными могут быть и части фигуры. Для этого они должны быть соразмерными относительно центра. То есть при предполагаемом сгибе фигуры по центру все точки двух половин должны совпасть в пространстве.
Свойства
Одно из свойств симметрии — движение. Это значит, что при изменении положения все точки окажутся на том же расстоянии друг от друга, что и были, то есть симметрия сохранится.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Изменение в пространстве предполагает поворот фигуры на 180°.
Центральная точка симметрии всегда неподвижна.
Прямая, проходящая через центр, симметрична сама себе.
Если прямая не проходит через центр, то она является параллельной. Это можно доказать путем построения двух прямых параллельных друг другу с центральной точкой, не лежащей ни на одной из линий. Соединяя симметричные точки, получим два равнобедренных треугольника, которые лежат накрест, а основания их останутся параллельными.
Формула
Так как точка симметрии является центральной, то отрезки прямой, симметричные относительно этой точки, должны быть равны. Представим линию, соединенную точками А и В. Центром пусть будет Х. Верным можно считать равенство АХ=АВ. Если происходит движение, то А переходит в точку А1, а В в В1. Центральная точка Х остается неподвижной. В этом случае АВ = А1В1.
Фигуры с центральной симметрией
К таким фигурам относится параллелограмм, так как в центральной точке пересекаются его диагонали. Каждая из фигур, получившаяся в результате пересечения, является симметричной.
У окружности центр находится посередине, а точки, лежащие на ней, являются симметричными.
Аналогичными свойствами обладают ромб и квадрат.
Как построить
Для построения симметрии относительно центральной точки, нужно начертить линию. Затем от одной из точек отложить отрезок, равный расстоянию между двумя первыми точками, и отметить третью. В результате вторая точка станет центром симметрии.
Примеры
Центральная симметрия часто встречается в окружающих нас предметах. В природе это любые круглые предметы: плоды кокоса, арбуза, томата, шапка одуванчика. Цветы симметричны относительно своей центральной части. Пчелиные соты представляют собой идеальные шестиугольники. Микроскопические капли воды, замерзая, образуют симметричные снежинки.
Симметрия свойственна многим предметам, созданным человеком: колесо, дорожные знаки, начертание букв.
Все виды симметрии, и центральная в частности, находят применение в строительстве и архитектуре. Принципа соразмерности придерживались все сторонники классицизма в искусстве.

В этом уроке мы вспомним понятия отображения плоскости на себя и движения плоскости, а также повторим основные понятия центральной симметрии. Затем введем аналогичные понятия и для пространства. Ответим на вопрос, будет ли центральная симметрия в пространстве являться движением пространства.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Центральная симметрия"
Сегодня на уроке мы вспомним понятия отображения плоскости на себя, движение плоскости, вспомним основные понятия центральной симметрии. Введём понятия отображения пространства и движение пространства, центральной симметрии в пространстве. Определим, будет ли центральная симметрия в пространстве – движением пространства.
Мы уже с вами знакомы с таким понятием, как движение. Давайте вспомним, что мы называли движением.
Движением мы называли любое отображение плоскости, которое сохраняет расстояние между точками.
Отображение плоскости на себя определяли так: если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причём любая точка плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение плоскости на себя.
Эти определения мы давали для движения на плоскости. Но в стереометрии мы говорим о пространстве, значит, надо определить, что называется движением пространства.
Но сначала давайте определим, что такое отображение пространства на себя.
Определение:
Пусть каждой точке пространства поставлена в соответствие некоторая точка , причем любая точка пространства оказалась поставленной в соответствие какой-то точке . Тогда говорят, что задано отображение пространства на себя. При данном отображении точка переходит (отображается) в точку .
Определение:
Под движением пространства понимается отображение пространства на себя, при котором любые две точки пространства и отображаются в какие-то точки и так, что .
По-другому можно сказать, что движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.
Теперь давайте вспомним, какие фигуры обладают центральной симметрией.
Определение:
Фигура называется симметричной относительно точки , если для каждой точки фигуры симметричная ей точка относительно точки также принадлежит этой фигуре. Точка называется центром симметрии фигуры.
Примерами центрально симметричных фигур можно назвать некоторые цветы:
В геометрии яркими примерами центрально симметричных фигур являются окружность (центр симметрии – центр окружности) и параллелограмм (центром симметрии является точка пересечения диагоналей).
Ещё мы давали такое определение:
Точки и называются симметричными относительно точки , если – середина отрезка .
В курсе планиметрии мы доказывали, что центральная симметрия является движением.
Напомним это доказательство.
Рассмотрим точки М и N и точки М1 и N 1 симметричные точкам М и N относительно точки О.
Рассмотрим треугольники М NО и М1ОN1.
То есть при центральной симметрии сохраняется расстояние между точками. Тогда по определению движения, получим, что и центральная симметрия является движением.
Определение:
В пространстве центральной симметрией мы назовём отображение пространства на себя, при котором любая точка переходит в симметричную ей точку относительно данного центра .
Теперь давайте докажем, что и в пространстве центральная симметрия является движением.
Пусть О – центр симметрии. Введём прямоугольную систему координат Оxyz с началом в точке О. Теперь давайте попробуем установить связь между координатами двух точек М (x, y, z) и М1(x1, y1, z1), симметричных относительно точки О.
Если точка М не совпадает с точкой О, то по определению центральной симметрии О – середина отрезка ММ1. Тогда координаты точки О можно вычислить по формулам координат середины отрезка. С другой стороны, поскольку О – начало координат, значит, точка О имеет координаты 0, 0, 0. То есть получим, что , , .
Если точки М и О совпадают, тогда точка М1 также совпадает с точкой О, потому что точка О – центр симметрии, а, значит, она отображается сама на себя. И в этом случае будут выполнятся равенства, , .
Теперь давайте рассмотрим две точки и .
По только что доказанным формулам для координат симметричных точек получим, что точка . Точка .
Теперь давайте найдём расстояние . Получим, что расстояние между точками , равно:
Теперь давайте найдём расстояние между точками и .
Вывод: расстояние между точками при центральной симметрии в пространстве сохраняется, значит, центральная симметрия в пространстве также является движением, но уже не плоскости, а пространства.
Рассмотрим несколько задач.
Задача: найти координаты точек, в которые переходят точки , , при центральной симметрии относительно начала координат.
Решение: воспользуемся формулами для вычисления координат симметричных точек.
Если точка симметрична точке то справедливы формулы:
Тогда получим, что точка отобразится в точку .
Точка отобразится в точку .
Точка отобразится в точку .
Решим ещё одну задачу.
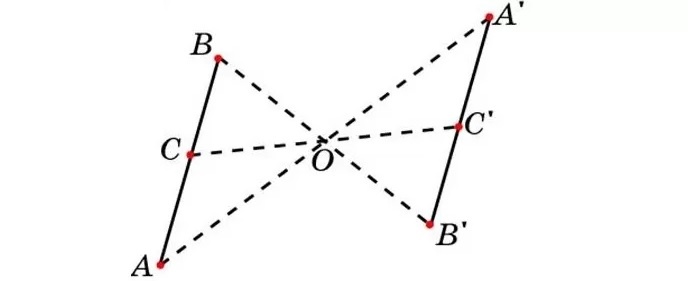
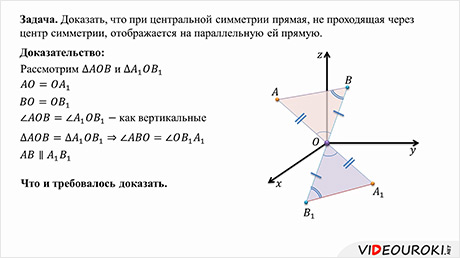
Задача: доказать, что при центральной симметрии прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.
Доказательство. Пусть прямая не проходит через центр симметрии О. Построим точки симметричные точкам и относительно точки О.
Рассмотрим и . По определению центральной симметрии точка О – середина отрезков АА1 и ВВ1, то есть и .
Тогда получим, что . Эти углы являются накрестлежащими для прямых и при секущей . Тогда по признаку параллельности прямых получим, что прямые . Что и требовалось доказать.
Сегодня на уроке мы вспомнили понятия отображения плоскости на себя, движение плоскости, вспомнили основные понятия центральной симметрии. Ввели понятия отображения пространства и движение пространства, центральной симметрии в пространстве. Показали, что и в пространстве центральная симметрия будет примером движения.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:


Содержание Центральная симметрия Задачи Построение Заключение

Центральная симметрия Точки М и М1 называются симметричными относительно точки А, если A – середина MM1 . A – центр симметрии A M M1

Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

Центральная симметрия Преобразование, переводящее каждую точку А фигуры в точку А1 , симметричную ей относительно центра О, называется центральной симметрией. ОПРЕДЕЛЕНИЕ: О О – центр симметрии (точка неподвижна) А А1 B B1 C C1

Фигуры, обладающие центром симметрии прямоугольник квадрат круг правильный шестиугольник параллелограмм ромб равносторонний треугольник правильный восьмиугольник

Фигуры,не обладающие центральной симметрией Неправильный многоугольник Произвольный треугольник Угол трапеция

Построение точки, симметричной данной отрезка, симметричного данному треугольника, симметричного данному

Построение точки, симметричной данной Определение ОМ = ОМ1 М1 – искомая точка О M M1

Построение отрезка, симметричного данному Определение А А1 О B B1 1. АО = А1О 2. ВО = В1О 3. А1В1 – искомый отрезок

Построение треугольника, симметричного данному Определение О А А1 B B1 C C1 2. ВО = В1 О 1. АО = А1О 3. СО = С1О 4. А1В1С1 – искомый треугольник

Задачи 1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О так, что АО≠ОВ. Симметричны ли точки А и В относительно точки О? 2. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат? А В С О 3. Постройте угол, симметричный углу ABC относительно центра О. Проверь себя

5. Для каждого из случаев, представленных на рисунке, постройте точки А1 и В1, симметричные точкам А и В относительно точки О. В А А В А В О О О О С М Р 4. Постройте прямые, на которые отображаются прямые a и b при центральной симметрии с центром О. Проверь себя Помощь

6. Постройте треугольники, симметричные данным, относительно точки О. О О Проверь себя Помощь

7. Постройте произвольный треугольник и его образ относительно точки пересечения его высот. 8. Отрезки АВ и А1В1 центрально симметричны относительно некоторого центра С. Постройте с помощью одной линейки образ точки М при этой симметрии. А В А1 В1 М 9. Найти на прямых a и b точки, симметричные относительно друг друга. a b O Проверь себя Помощь

Проверь себя! 1. Нет, т.к. по условию АО≠ОВ. 2. а) да, середина отрезка; б) нет; в) да, точка пересечения прямых; г) да, точка пересечения диагоналей. 3. А В С О В1 А1 В1 назад

Проверь себя! О С М Р 4. С1 Р1 М1

Проверь себя! В А О А В А В О О В1 А1 В1 А1 А1 В1 5. назад

Проверь себя! О О назад 6.

Проверь себя! А В А1 В1 М М1 8. a b O 9. Х Х1 b1 назад

Краткое описание документа:
Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Преобразование, переводящее каждую точку А фигуры в точку А1 , симметричную ей относительно центра О, называется центральной симметрией.
Центральная симметрия – самая интересная и познавательная тема в геометрии, которую изучают в начальных классах школы и более тщательно — в 8 — 11 классах. Знания по этой теме обязательно пригодятся ученику в жизни.
Что такое центральная симметрия
Начнём с определения: центральная симметрия — одно из свойств определённой геометрической фигуры, при котором точке В соответствует некая точка В1, находящая в таком же пространственном положении относительно точки С. Точка С лежит на середине отрезка ВВ1. Точка С называется центром симметрии. Это определение соответствует курсу планиметрии.

Центральную симметрию можно построить и в пространстве. В пространстве центральной симметрией называется словно зеркальное отображение какой-либо геометрической фигуры. Она представляет собой две одинаковые фигуры, соответственные точки которых попарно симметричны относительно точки пространства О.
Свойства центральной симметрии
Основные свойства следующие:
1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.
Посмотрим на рисунок. Треугольники АВС и А1В1С1
симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А1О, ВО=В1О, СО=С1О. Значит, картинка остаётся той же.

Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;
2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;
3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;
4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.
Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А1В1 относительно точки О.

Далее соединяем симметричные точки и получаем отрезки АА1 и ВВ1. Далее легко заметить, что отрезки АО и А1О будут равны. Соответственно равны и отрезки ВО и В1О. Углы, которые образуются при пересечении двумя прямыми точки О также равны.
Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А1 и В,В1. Значит они являются накрест лежащими при секущих АА1 и ВВ1. Задача решена, АВ и А1В1 параллельны;
5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.
Примеры фигур, обладающих центральной симметрией

Фигур, как имеющих углы, так и без углов, но при этом обладающих центральной симметрией не так уж мало:
различные правильные многоугольники.
Интересные факты о центральной симметрии
Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией.

Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке.
Ещё один очевидный пример – бабочка.

Великолепные узоры на её крылышках – четкая и яркая симметрия.
Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.
Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия.

Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.
Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.
Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.
Читайте также:

