Сообщение на тему объем тела

Обновлено: 02.07.2024

Презентация на тему: " Объёмы тел Понятие объёма Понятие объёма Свойства объёмов Свойства объёмов Объём прямоугольного параллелепипеда Объём прямоугольного параллелепипеда Объём." — Транскрипт:

1 Объёмы тел Понятие объёма Понятие объёма Свойства объёмов Свойства объёмов Объём прямоугольного параллелепипеда Объём прямоугольного параллелепипеда Объём прямой призмы Объём прямой призмы Объём наклонной призмы Объём наклонной призмы Объём пирамиды Объём пирамиды Объём цилиндра Объём цилиндра Объём конуса Объём конуса Объём шара Объём шара Объём шарового сегмента Объём шарового сегмента Объём шарового сектора Объём шарового сектора

2 Понятие объёма За единицу измерения объёмов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называют кубическим сантиметром и обозначают см 3. Аналогично определяются кубический метр (м 3 ), кубический миллиметр (мм 3 ). При выбранной единице измерения объём каждого тела выражается положительным числом, которое показывает, сколько единиц измерения объёмов и частей единицы содержится в данном теле. 1 м 3 1 см 3 1 мм 3

3 Свойства объёмов I свойство Равные тела имеют равные объёмы. (Два тела называются равными, если их можно совместить наложением). a b c a b c h a h a

4 Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел. Свойства объёмов II свойство F Q V = V F + V Q L P V = V L + V P

5 Объём прямоугольного параллелепипеда Объём прямоугольного параллелепипеда равен произведению трёх его измерений. a b c V = abc

6 Следствие I Объём прямоугольного параллелепипеда равен произведению площади основания на высоту. Объём прямоугольного параллелепипеда a b c ab = S c = h V = Sh h S

7 Следствие II Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. Объём прямоугольного параллелепипеда C A A1A1 B B1B1 C C1C1 D D1D1 S h A1A1 A B B1B1 C1C1 S h V = Sh

8 Объём прямой призмы Объём прямой призмы равен произведению площади основания на высоту. S h V = Sh

9 Объём наклонной призмы Объём наклонной призмы равен произведению площади основания на высоту. S h V = Sh

10 Объём пирамиды Объём пирамиды равен одной трети произведения площади основания на высоту. h S

11 Следствие Объём V усечённой пирамиды, высота которой равна h, а площади оснований равны S и S 1, вычисляется по формуле: Объём пирамиды h S S1S1

12 Объём цилиндра Объём цилиндра равен произведению площади основания на высоту. r h

13 Объём конуса Объём конуса равен одной трети произведения площади основания на высоту. r h

14 Следствие Объём V усечённого конуса, высота которого равна h, а площади оснований равны S и S 1, вычисляется по формуле: Объём конуса r1r1 r h S S1S1

15 Объём шара Объём шара радиуса R равен. R

16 Объём шарового сегмента Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. R шаровой слой h шаровой сегмент

17 Объём шарового сектора Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 90, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов. R r h

ГОСТ

Понятие объема

Понятие объема тел будем связывать с такой геометрической фигурой, как куб. За единицу объема фигуры будем принимать объем куба с ребром, равным единице. Из этого очевидно, что объем куба будет равняться кубу длины его ребра. Введем несколько свойств, для понятия объема геометрических фигур.

У равных геометрических тел равные объемы.

Тело, состоящее из нескольких тел, имеет своим объемом сумму объемов тел, из которых оно состоит.

Одной из основных формул для вычисления объемов тел является формула вычисления объема тел с помощью определенного интеграла:

Здесь $S\left(x\right)$ - функция площади сечения фигуры плоскостью, перпендикулярной оси $Ox$ (рис. 1).

Выведем теперь объемы фигур, хорошо известных в курсе стереометрии. Для это будем рассматривать поиск объемов как задачи на использование формулы нахождения объема с помощью интеграла.

Объем прямоугольного параллелепипеда

Доказать, что объем прямоугольного параллелепипеда определяется как произведение ширины, высоты и длины данного параллелепипеда.

Доказательство.

Обозначим высоту параллелепипеда через $c$, ширину через $b$ и длину через $a$. Выберем одну из вершин как начало координат и проведем ось $Ox$ через длину параллелепипеда (рис. 2.).

Проводя сечения, перпендикулярно $Ox$ будем получать прямоугольники с площадью $S\left(x\right)=bc$. Используя формулу для вычисления объема тел, получим

Объем призмы

Доказать, что объем призмы определяется как произведение площади основания этой призмы на высоту.

Доказательство.

Рассмотрим произвольную призму, проведем в ней высоту и построим ось $Ox$ через эту высоту, считая началом координат точку $O$ основания высоты (рис. 3).

Проводя сечения, перпендикулярно $Ox$ будем получать многоугольники с $S\left(x\right)=S_$. Используя формулу для вычисления объема тел, получим

Готовые работы на аналогичную тему

Объем цилиндра

Доказать, что объем цилиндра определяется как произведение площади основания цилиндра на его высоту.

Рассмотрим произвольный цилиндр, проведем в нем высоту и построим ось $Ox$ через эту высоту, считая началом координат точку $O$ основания высоты (рис. 4).

Проводя сечения, перпендикулярно $Ox$ будем получать окружности с $S\left(x\right)=\pi r^2$. Используя формулу для вычисления объема тел, получим

Объем шара

Доказать, что объем шара определяется следующей формулой

Доказательство.

Пусть нам дан шар с радиусом, равным $R$. Проведем через центр сферы произвольно ось $Ox$ (рис. 5).

Проведем через произвольную точку $O_1$ сечение, перпендикулярное оси $Ox.$ Данное сечение является окружностью. Обозначим ее радиус через $r$. Так как точка выбрана произвольно, то площадь окружности можно считать функцией от абсциссы $x$. Обозначим её через $S(x)$. Нам известно, что $S\left(x\right)=\pi r^2$. По теореме Пифагора, получим

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Лекция 13. Объем геометрического тела и его измерение.

Объем– это положительная скалярная величина, характеризующая размер геометрического тела.

Объемом тела называется положительная скалярная величина, определенная для каждого геометрического тела так, что:

1. равные тела имеют равные объемы;

2. если тело составлено из нескольких тел, то его объем равен сумме их объемов.

Будем объем тела Q обозначать V(Q).

Чтобы измерить объем тела, нужно выбрать единицу объема. Таковой является куб со стороной, равной единице длины, его объем равен е 3 . Измерение объема состоит в сравнении объема данного тела с объемом единичного куба. Результатом этого сравнения является такое число х такое, что V(Q) = х ∙ е 3 , которое называют численным значением объема при данной единице объема.

Свойства численных значений объема

1. Если тела равны, то равны и численные значения их объемов:

Q ₁ = Q ₂ V(Q ₁ ) = V(Q ₂ ).

2. Если тело Q состоит из тел Q ₁ , Q ₂ ,…, Q _n , то численное значение объема тела равно сумме численных значений объемов этих тел.

3. При замене единицы измерения объема численное значение объема увеличивается (уменьшается) во столько раз, во сколько раз уменьшается (увеличивается) единица объема.

Выразим, например, 9 дм 3 в кубических сантиметрах. Известно, что 1 дм 3 = 1000 см 3 , и, следовательно, 9 дм 3 = 9 ∙ 1 дм 3 = 9 ∙ (1000 см 3 ) = (9 ∙ 1000) ∙ см 3 = = 9000 см 3 .

Для измерения объемов площадей используют стандартные единицы площади: м 3 , дм 3 , см 3 , мм 3 . Основная единица измерения объема – кубический метр. Соотношения между единицами объема: 10 -9 км 3 = 1 м 3 = 10 3 дм 3 = 10 6 см 3 = 10 9 мм 3 .

Объем прямоугольного параллелепипеда равен произведению трех его измерений.

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

Объем прямой призмы равен произведению площади основания на высоту.

Объем наклонной призмы равен произведению площади основания на высоту.

Объем пирамиды равен одной трети произведения площади основания на высоту.

Объем прямого цилиндра равен произведению площади основания на высоту.

Объем конуса равен одной трети произведения площади основания на высоту.

Объем усеченного конуса, высота которого равна , а площади оснований и , вычисляется по формуле .

Объем шара радиуса равен.

Задания для самостоятельной работы по теме:

Ребро данного куба равно 1/3 ребра единичного куба. Чему равен объем данного куба?

Найдите объем правильной четырехугольной пирамиды, сторона которого 5см., а высота 8 см.

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Объемы геометрических тел

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

V сохраняется при движениях.
V удовлетворяет принципу Кавальери.
Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

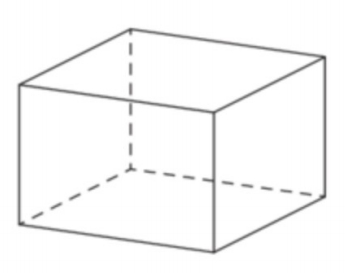
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

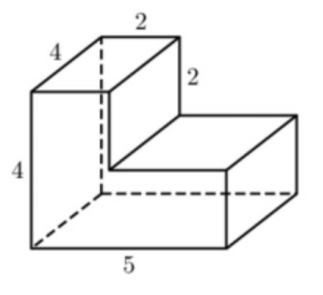
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

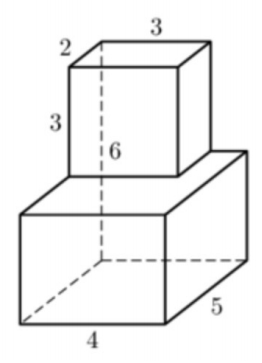
Разберем, как можно вычислять объемы изучаемых в школе фигур.

Объем призмы

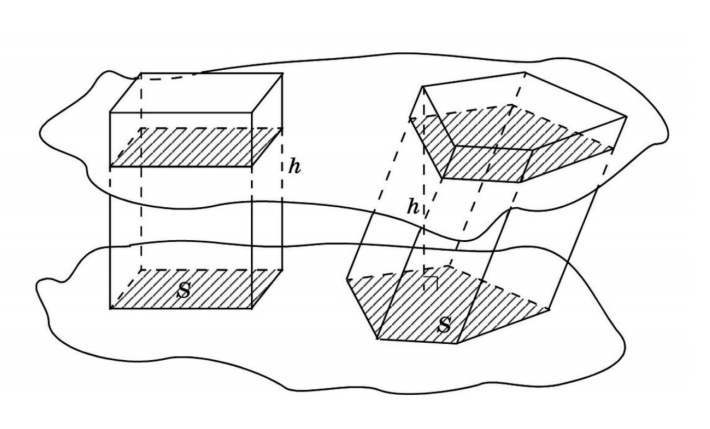
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

V S_осн h

Задачник является Частью УМК для 10-11 классов, предназначенного для изучения предмета на углубленном уровне, и содержит более 1000 задач разной степени трудности, помогающих изучению и усвоению материала, изложенного в учебнике. Пособие соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования.

Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

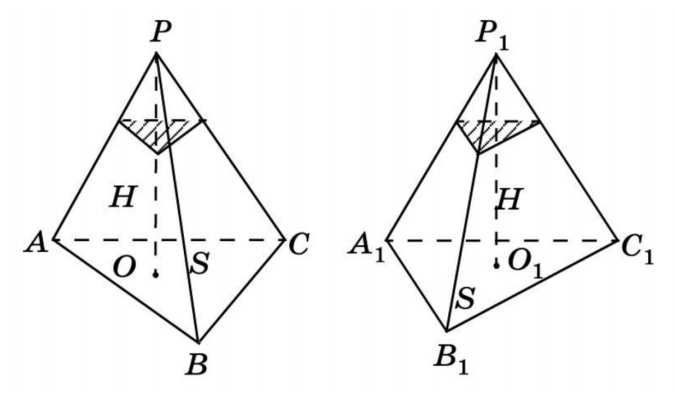
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V ₁/V₂ = 1 V₁= V₂

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

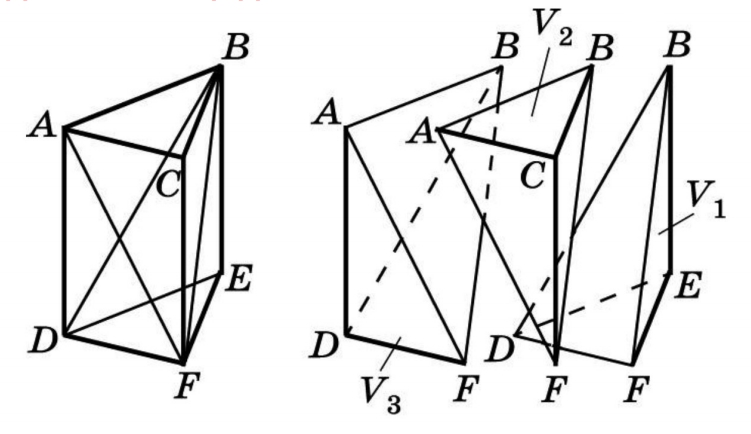
V_призмы S h = 3V

Объем цилиндра

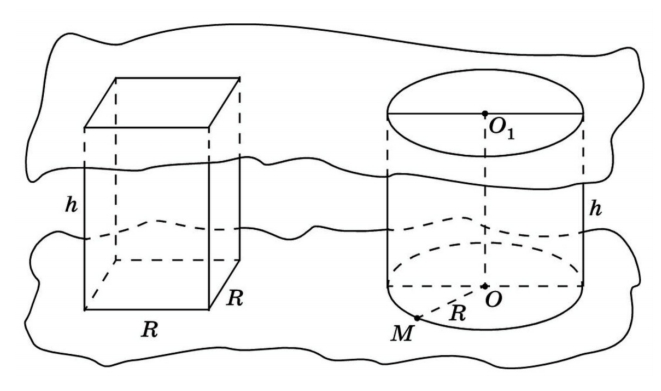
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

V_цил = πh × R 2

Объем конуса

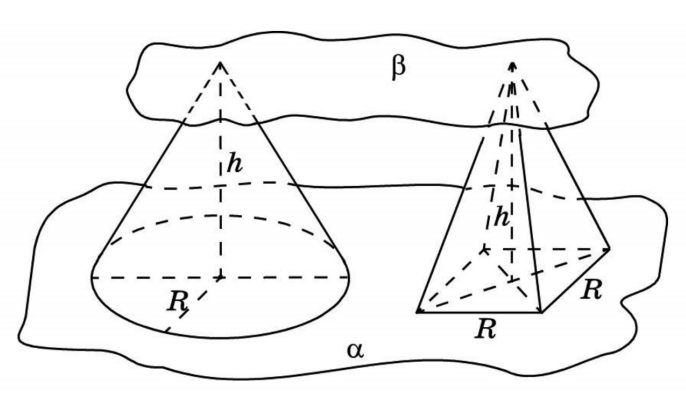
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

S_Ф1/S_Ф2 = π

V_конуса = 1/3 πR 2 h

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR 2 . Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x 2 . Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R 2 — x 2 ).

Заметим, что: πR 2 + πR 2 — πR 2 = πR 2

V_цил = πR 2 × R = πR 3 = 1/3 R 3 π + V_шара

V_шара = 4/3 πR 3

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

Читайте также: