Задача о диете реферат

Обновлено: 31.05.2024

Предприятие может выпускать определенные виды продукции, используя для этого различные виды ресурсов. Известны затраты каждого вида ресурса на производство единицы каждого вида продукции и прибыль от реализации единицы каждого вида продукции. Требуется составить план выпуска продукции, чтобы при данных запасах ресурсов получить максимальную прибыль.

Составим математическую модель данной задачи.

i - номер i -го вида ресурса, ;

b _i - запасы i -го вида ресурса, ;

j - номер j -го вида продукции, ;

a _ij - затраты i -го вида ресурса на производство единицы j -го вида продукции;

c _j - прибыль от реализации единицы j -го вида продукции.

Все данные занесем в таблицу:

1 2 … j … n

Прибыль от реализации

Обозначим через x _j - планируемый выпуск j -го вида продукции; - план выпуска продукции. Тогда прибыль от реализации всей выпускаемой продукции составит

Составим ограничения по ресурсам. Найдем расход первого вида ресурса:

Первый вид ресурса имеется в наличии b ₁ условных единиц, т.е. получаем ограничение a ₁₁ x ₁ + a ₁₂ x ₂ +…+ a _{1 j} x _j +…+ a _{1 n} x _n £ b ₁ .

Аналогично составляем ограничения по всем остальным видам ресурсов.

Кроме того, x _j ³ 0, , так как количество продукции не может быть отрицательным числом.

Получим ЗЛП: найти наибольшее значение функции при ограничениях:

Таким образом, математической моделью данной задачи является ЗЛП.

Задача о диете

В продаже имеются различные виды продуктов. Известны содержания питательных веществ в единице каждого вида продукта, цена продуктов, медицинские требования на содержание питательных веществ в суточной диете. Требуется определить, какие продукты и в каком количестве нужно включить в диету, чтобы она соответствовала всем медицинским требованиям и чтобы стоимость диеты была минимальной.

Составим математическую модель данной задачи.

j - номер j -го продукта, ;

i - номер i -го питательного вещества, ;

a _ij -содержание i -го питательного вещества в единице j -го продукта;

b _i - минимальное содержание i -го питательного вещества в суточной диете;

c _j - цена единицы j -го продукта.

Все данные занесем в таблицу:

1 2 … j … n

Цена единицы продукта

Пусть x _j единиц j -го продукта включается в суточную диету, тогда - суточная диета.

Если в диету включаем x ₁ , x ₂ , …, x _n единиц каждого продукта, то содержание первого питательного вещества в диете составит

и это должно быть не менее чем b ₁ единиц, т.е. получаем неравенство

Аналогично составляем ограничения по всем видам питательных веществ.

Кроме того, x _j ³ 0, так как количество продуктов не может быть отрицательным числом.

Математическая модель задачи: найти минимум функции

Таким образом, математической моделью данной задачи является ЗЛП.

Задача на оптимальный раскрой материала (по длине)

Имеются прутки одинаковой длины, из которых нужно нарезать определенное количество заготовок заданной длины. Прутки можно нарезать на заготовки по различным вариантам. При каждом варианте нарезания прутков остаются концевые отрезки.

Требуется определить, какое количество прутков следует разрезать по каждому варианту, чтобы получить заданное количество заготовок различной длины и чтобы общая длина концевых отрезков была минимальной.

Составим математическую модель данной задачи.

i - номер i -го вида заготовки, ;

j - номер j -го варианта раскроя прутка, ;

a _ij - количество заготовок i -го вида, получаемых из одного прутка, разрезаемого по j - му варианту;

b _i - требуемое число заготовок i -го вида;

c _j - длина концевого отрезка, оставшегося от одного прутка при разрезании прутка по j - му варианту.

Все данные занесем в таблицу:

1 2 … j … n

Длина концевого отрезка

Обозначим через х _j - число прутков, разрезаемых по j - му варианту, тогда - план раскроя прутков. Найдем общую длину концевых отрезков.

По первому варианту планируем разрезать x₁ прутков, концевой отрезок от одного прутка будет иметь длину с₁, тогда общая длина концевых отрезков от х₁ прутков составит c₁ x₁. Аналогично, общая длина концевых отрезков от х₂ прутков, разрезанных по второму варианту, будет равна c₂x₂ и т.д.

Следовательно, общая длина концевых отрезков при разрезании прутков по всем вариантам

Составим ограничения по заготовкам.

Заготовок первого вида получают из одного прутка, разрезаемого по первому варианту, a ₁₁ штук, а из x ₁ прутков - a ₁₁ x ₁ ; по второму варианту из одного прутка получают a ₁₂ штук, а из x ₂ прутков - a ₁₂ x ₂ и т.д., по n - му варианту - a _{1 n} x _n штук. Отсюда получаем первое ограничение

Аналогично получаем ограничения по всем заготовкам.

Кроме того, так как число прутков не может быть отрицательным.

Математическая модель задачи: найти наименьшее значение функции

Таким образом, математической моделью данной задачи является ЗЛП.

Пример 1 . Имеются прутки длиной 1 м . Требуется нарезать 200 заготовок длиной 25 см , 250 заготовок длиной 30 см и 150 заготовок д линой 35 см . Количество заготовок, которые можно нарезать из одного прутка по различным вариантам, а также длина концевых отрезков даны в таблице:

Дама просто приятная решила похудеть и, как это нередко случается, обратилась за советом к подруге. Подруга – дама приятная во всех отношениях, посоветовала ей перейти на рациональное питание, состоящее из двух новомодных продуктов Р и Q.

Дневное питание этими новинками должно давать не более 14 единиц жира (чтобы похудеть), но и не менее 300 калорий (чтобы не сойти с дистанции раньше). На банке с продуктом Р написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150 калорий, а на банке с продуктом Q – 4 единицы жира и 200 калорий соответственно. При этом цена 1 кг продукта Р равна 15 у.е., а 1 кг продукта Q – 25 у.е.

Так как дама просто приятная в это время была несколько стеснена в средствах, то ее интересовал ответ на следующий вопрос: в какой пропорции нужно брать эти удивительные продукты Р и Q для того, чтобы выдержать условия диеты и истратить как можно меньше денег?

1. Построение модели. Обозначим через х количество продукта Р, а через у количество продукта Q, требуемые для выполнения условий диеты.

Количество единиц жира, содержащегося в х кг продукта Р и в у кг продукта Q, равно 15х + 4у и по условию диеты не должно превосходить 14. Поэтому .

В свою очередь, количество калорий, содержащихся в х кг продукта Р и в у кг продукта Q, равно 150х + 200у и должно быть не меньше 300. Значит, .

Теперь о стоимости продуктов. Она равна z(х; у) = 15x + 25y и в соответствии с высказанными пожеланиями должна быть минимальной. Последнее записывается так: z(х; у) = 15x + 25y → min.

Итак, мы получили систему неравенств

которая является математической моделью задачи.

Полученная система неравенств называется системой ограничений задачи, а функция z(х; у) называется целевой функцией задачи.

2. Решение математической задачи, к которой приводит модель. Для решения применим координатно-графический метод.

Решением системы ограничений является многоугольник, полученный путем пересечения областей решений всех неравенств системы. Решением линейного неравенства является одна из полуплоскостей, на которые прямая, соответствующая данному неравенству, делит координатную плоскость. Для определения искомой полуплоскости берется точка, не лежащая на прямой, ее координаты подставляются в неравенство. Если в результате получается верное числовое неравенство, то решением является полуплоскость, содержащая выбранную точку. В противном случае, решением является другая полуплоскость.

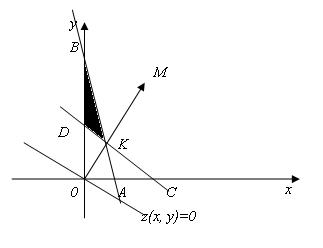
Введем на плоскости прямоугольную систему координат хОу и построим многоугольник решений системы ограничений нашей задачи.

Из условий х ≥ 0 и у ≥ 0 вытекает, что все точки, которые удовлетворяют системе ограничений, лежат в первой координатной четверти.

Теперь решим неравенство . Ему соответствует прямая, заданная уравнением , которая проходит через точки и . Для проверки возьмем точку О(0; 0): 15 · 0 + 4 · 0 = 0 ≤ 14. Так как 0 ≤ 14 – верное неравенство, то решением неравенства является полуплоскость, содержащая точку О.

Обращаясь подобным же образом с неравенством , находим точки пересечения прямой с осями координат – точки С(2; 0) и D(0; 1,5). Для проверки также возьмем точку О(0; 0): 150 · 0 + 200 · 0 = 0 ≥ 300. Так как 0 ≥ 300 – неверное числовое неравенство, то решением неравенства является полуплоскость, не содержащая точку О.

Пересечением всех полуплоскостей является треугольник BDK. Точка К является точкой пересечения прямых АВ и CD и имеет координаты .

Теперь среди всех точек треугольника найдем ту, координаты которой удовлетворяют условию минимальности целевой функции z.

Для этого построим так называемую линию нулевого уровня функции z, которая задается уравнением z(x; y) = 0. Будем двигать эту прямую в направлении вектора , координаты которого являются соответствующие коэффициенты целевой функции, до места первой встречи этой прямой с треугольником BDK. Искомой точкой будет точка К . То есть искомые значения х = , у = 1.

3. Интерпретация полученных следствий из математической модели. Таким образом, чтобы выполнить условия диеты и истратить при этом как можно меньше средств, продукты Р и Q нужно брать в отношении х : у = : 1 = 2 : 3. То есть на 2 части продукта Р брать 3 части продукта Q.

Выводы

Модель – это условный образ объекта, построенный для упрощения его исследования.

Конечно, при попытке упрощенного описания ситуации некоторыми обстоятельствами приходится пренебрегать, считая их несущественными. Однако единого взгляда на то, что именно существенно, а что не очень, по-видимому, нет. Можно, например, не обращать внимания на то, что начался дождик. Но одно дело пробежать под накрапывающим дождем сотню метров, и совсем другое – часовая прогулка под таким дождем без зонта.

Предлагая построенную или выбранную нами модель, мы непременно должны указывать пределы, в которых ею можно пользоваться, и предупреждать о том, что нарушение этих ограничений приводит (и, скорее всего, приведет) к серьезным ошибкам. Коротко говоря, у каждой модели есть свой ресурс.

Покупая блузку или рубашку, мы привыкли к наличию меток, на которых указаны максимально допустимая температура глажения, дозволенные виды стирки и т.п. Это, конечно, ни в коей мере не означает, что нам запрещается, взяв докрасна раскаленный утюг, пройтись им по ткани раз-другой. Такое мы сделать можем. Но вот захотим ли мы носить блузку или рубашку после такого глажения?

Таким образом, построение модели опирается на значительное упрощение изучаемой ситуации и, следовательно, к получаемым на ее основе выводам нужно относиться достаточно осторожно – модель может не все.

Вместе с тем, даже весьма грубая на вид идеализация нередко позволяет глубже вникнуть в суть проблемы. Пробуя как-то влиять на параметры модели (выбирать их, управлять ими), мы получаем возможность подвергнуть исследуемое явление качественному анализу и сделать выводы общего характера.

Контрольные вопросы:

1.Что такое модель, моделирование?

2.Какие два подхода различают в моделировании? В чем их особенность?

3.Перечислите типы моделей. Дайте им краткую характеристику.

4.В чем важность математического моделирования?

5. Перечислите этапы математического моделирования. Охарактеризуйте каждый этап.

6.Как можно классифицировать математические модели?

7.Приведите пример задачи математического моделирования.

8. Почему нужно с осторожностью относиться к выводам, полученным на основе модели?

Сформулированная задача является задачей линейного программирования общего типа. Поставленную здесь задачу выбора оптимального рациона питания часто называют также задачей о диете или задачей о смесях. [c.177]

Противоположна изложенной другая задача Л.п. поиск минимума функции при заданных ограничениях. Такая задача возникает, напр., когда требуется найти наиболее дешевую смесь некоторых продуктов, содержащих необходимые компоненты (см. Задача о диете). При этом известно содержание каждого компонента в единице исходного продукта — а. ее себестоимость — с задается потребность в искомых компонентах — Ъ.. [c.172]

Задачи Л.п., в которых нормативы (или коэффициенты), объемы ресурсов (константы ограничений) или коэффициенты целевой функции содержат случайные элементы, называются задачами линейного стохастического программирования когда же одна или несколько независимых переменных могут принимать только целочисленные значения, то перед нами задача линейного целочисленного программирования. В экономике широко применяются линейно-программные методы решения задач размещения производства (см. Транспортная задача), расчета рационов для скота (см. Задача диеты), наилучшего использования материалов (см. Задача о раскрое), распределения ресурсов по работам, которые надо выполнять (см. Распределительная задача) и т.д. [c.172]

ЗАДАЧА ДИЕТЫ (или задача о рационе) — задача линейного программирования, состоящая в определении такого рациона, который удовлетворял бы потребности человека или животного в питательных веществах при минимальной общей стоимости используемых продуктов. Это частный (наиболее распространенный) случай более общей задачи об оптимальном составе смеси. [c.119]

Задача о смесях (диете). Имеются нек-рые исходные продукты в заданных объёмах. Применяется неск. видов смесей из этих продуктов, известны отпускные цены каждой смеси. Требуется подобрать их так, чтобы они получались из заданных объёмов исходных продуктов и суммарная отпускная цена была наименьшей. Эта задача встречается при составлении кормовых рационов в сельском х-ве, при выпуске нефтепродуктов, при составлении плана выпуска тканей. [c.356]

Если бы эта книга была о соблюдении диеты, представьте себе, как вы радовались бы, когда сбросили бы первые килограммы своего веса. Взгляните на управление временем под этим углом зрения. Каждая задача, вычеркнутая из вашего списка, приближает вас к поставленной цели. На чашу весов может быть брошена не только тяжесть задачи, вы стараетесь совершить нечто более сложное - избавиться от излишней потери времени. Ваша цель - добиться хорошо спланированного дня со свободным временем. [c.43]

Необходимо разработать путь достижения этих целей, иметь четкие представления о том, как вы собираетесь добиваться этого, поставить перед собой конкретные задачи и работать над ними. Не раздумывайте - приступайте к делу тотчас же. Поставьте себе несколько задач самостоятельно и посмотрите, как вы с ними справитесь. Если сразу не получается или вы чувствуете, что зашли в тупик, сядьте и подумайте. Поищите то, что помогает вам сэкономить несколько минут в день. Вспомним пример с человеком, сидящим на диете даже в первую неделю, если он следует инструкциям и своим собственным целям, он сможет почувствовать разницу. [c.44]

Становление современного математического аппарата оптимальных экономических решений началось в 40-е годы, благодаря первым работам Н. Винера, Р. Беллмана, С. Джонсона, Л. Канторовича. Задача линейного программирования впервые математически сформулирована Л. В. Канторовичем в 1939 г. на примере задачи раскроя материалов для Ленинградского фанерного треста. В 1947 г. Дж. Данциг предложил универсальный алгоритм решения задач линейного программирования, названный им симплекс-методом. В 1941 г. Хичкок и независимо от него в 1947 г. Купсман формулируют транспортную задачу, в 1945 г. Стиглер — задачу о диете. В 1952 г. было проведено первое успешное решение задачи линейного программирования на ЭВМ Sea в Национальном бюро стандартов США. [c.102]

Задача о диете или задача об оптимизации смеси (упрощенный вариант). Предположим, что необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ (тиамина Т и ниацина Н). Пищевая ценность рациона (в калориях) должна быть не меньше заданной. Пусть для простоты смесь для цыплят изготавливается из двух продуктов К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Какое количество К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу (или больше) веществ Н и Т и калорий, а стоимость порции была минимальна Исходные данные для расчетов приведены в табл. 1.7. [c.165]

Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, как былб в задаче о диете, можно похожим, но несколько более сложным образом выделить его обращенную к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед. [c.169]

ЗАДАЧА ДИЕТЫ [nutrient problem] (или задача о рационе питания) — задача линейного программирования, состоящая в определении такого рациона, который удовлетворял бы потребности человека или животного в питательных веществах при минимальной общей стоимости используемых продуктов. Это частный (наиболее распространенный) случай более общей задачи об оптимальном составе смеси. Задача составления оптимального рациона для человека сложна, так как приходится учитывать много дополнительных, не всегда формализуемых факторов вкусовые привязанности, разнообразие блюд и т.д. Однако в животноводстве определение рационов для скота с помощью задачи линейного программирования сегодня не просто реально, но и необходимо. Опыт показывает, что кормление скота рационами, рассчитанными по этому методу, дает существенную экономию (напр., в США ими пользуются многие фермеры). Это не означает, разумеется, что каждый сам решает задачу линейного программирования в разных районах [c.99]

Современная вычислительная техника дает возможность применения экономико-математических методов для решения указанной проблемы. Формализация данной задачи чащв всего осуществляется согласно математической модели классической задачи линейного программирования "о диета". [c.47]

Член-корреспондент АН СССР А. Г. Аганбегян рассказывал о том, как, будучи еще студентом, он задумал с noMoaibio математики рассчитать себе наиболее дешевый бюджет питания. Из работ по рациональному питанию он выбрал, показатели, характеризующие количество различных питательных веществ (жиров, белков, углеводов и т. п.), необходимых для здорового человека, затем по поваренной книге выписал примерно 60 продуктов и их питательный состав и приступил к решению. Он составил модель линейного программирования, в которой переменными служили виды продуктов и их цены, а целевой функцией — стоимость рациона. Результаты поразили молодого экономиста. Оказалось, что в оптимальный набор попали только пять продуктов, в том числе 800 г ржаной муки, около 3 кг капусты и т. д. Это показало, что для человека не так-то проста задача составления диеты — надо участь много дополнительных, не всегда формализуемых факторов вкусовые привязанности, разнообразие блюд и т. д. [c.119]

Смотреть страницы где упоминается термин Задача о диете

Математические методы моделирования экономических систем Изд2 (2006) -- [ c.196 ]

Предположим, что в дневной рацион животных должны входить питательные вещества двух видов в количестве, заданном в таблице.

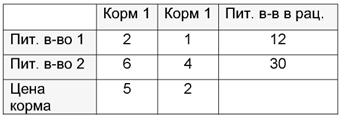
Имеется возможность составлять рацион из кормов двух видов, для которых задано содержание питательных веществ в единице корма и цена одной единицы каждого из видов кормов. При удовлетворении условий по необходимому содержанию питательных веществ в данном рационе требуется достичь его минимальной стоимости.

Пусть х1 и х2 - содержание в данном рационе единиц корма 1-го и 2-го вида соответственно. Общую стоимость дневного рациона запишем, используя цены на корма:

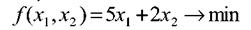
Ограничения имеют следующую структуру:

содержание пит, веществ в рационе ≥ min кол-во пит, в-в.

Используя для записи левой части введенные неизвестные, получим

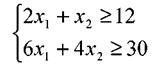
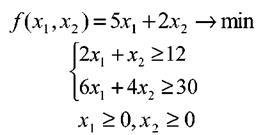
Добавив к полученным ограничениям условия неотрицательности (х1 равно нулю, если корм i не используется в рационе), окончательно запишем ЗЛП.

В приведенных примерах все ограничения имеют вид линейных неравенств. Это, так называемые, нежесткие ограничения (ресурс может быть израсходован полностью, а может и частично). Однако можно ставить и жесткие ограничения в виде линейных уравнений. Так, в первом примере, требование полного использования ресурса 1-го вида

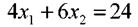
приводит к ограничению:

Теория графов и графовые сети (или просто графы) используются практически во всех областях знаний, в том числе, в компьютерной науке и практике. Основное достоинство графов в том, что их можно рисовать на бумаге или экранах компьютеров в виде точек соединенных стрелками и/или линиями. Вместе с тем, связанный граф представляется формально с помощью наборов бинарных отношений и/или множеств, каждое их которых состоит из двух элементов. Графы рисуют на бумаге не только те кто понимают теорию графов, но и люди, которые никогда о ней не слышали. К примеру, любой администратор, изображающий структуру, подчиненных ему подразделений в виде прямоугольников и стрелок между ними, по сути дела, рисует связанный ориентированный граф, хотя он и не знает об этом.

Графом называется набор точек (эти точки называются вершинами), некоторые из которых объявляются смежными (или соседними). Считается, что смежные вершины соединены между собой ребрами (или дугами).

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Таким образом, ребро определяется парой вершин. Два ребра, у которых есть общая вершина, также называются смежными (или соседними).

Граф называется ориентированным (или орграфом), если некоторые ребра имеют направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Геометрически граф часто изображают точками плоскости, причем соседние вершины соединены дугами (для орграфа некоторые дуги имеют направление, что обычно отмечают стрелкой).

Помимо этого, в теории графов рассматриваются также мультиграфы – это такие графы, в которых могут быть петли (т. е. некоторая вершина соединена сама с собой ребром) или некоторые пары вершины могут быть соединены между собой несколькими ребрами.

Маршрут в графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежных ребер (в этом случае ребра приобретают направление). Заметим, что в маршруте могут повторяться вершины, но не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней.

Путь в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер).

Контур – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.

Последовательности вершин (рис. 1): 1–2–3–4–2–5 не простой путь, а маршрут; последовательности 1–2–3–4–7–5 и 1–2–5 – простые пути; 1–2–3–4–2–5–6–1 –это цикл (но не контур); 1–2–5–6–1 – это контур.

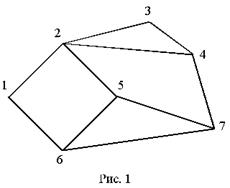
Если имеется некоторый маршрут из вершины t в вершину s, заданный в виде последовательности ребер, которые в этом случае приобрели направление, и если в этот маршрут входит ребро, соединяющее вершины (i, j), то это ребро по отношению к вершине i называют иногда прямой дугой, а по отношению к вершине j – обратной дугой (или обратным ребром).

Граф называется связным, если любые две его вершины можно соединить маршрутом (или путем). На рис. 1 изображен связный граф.

Ребро, при удалении которого граф перестает быть связным, иногда называют мостом или перешейком.

Следующее определение имеет смысл только для графов или мультиграфов без петель (но не для орграфов).

Степень вершины – это число ребер, входящих в эту вершину. Вершина называется висячей, если ее степень равна единице.

Лемма 1. Если степень всех вершин в графе больше или равна двум, то граф обязательно содержит контур.

Читайте также:

  
• Логика пор рояля реферат
  
• Психология личностный конструктор реферат
  
• Потерпевший в уголовном процессе реферат
  
• Реферат т с элиот
  
• Собственность в ссср реферат