Векторное поле определение привести пример реферат
Обновлено: 30.06.2024
Примеры векторных полей: 1) поле скоростей текущей жидкости;
2) силовые поля: электрическое, магнитное, гравитационное.
Векторное поле считается заданным, если в каждой его точке М определена векторная функция . Если векторное поле отнесено к декартовой системе координат, то векторную функцию можно записать в виде:
Простейшей геометрической характеристикой векторного поля являются векторные линии.
Векторные линии – это линии, в каждой точке которой касательная имеет направление соответствующего ей вектора.
Примеры векторных линий: 1) если рассматривается поле скоростей текущей жидкости, то векторные линии суть линии тока этой жидкости, т.е. траектории движения частиц жидкости; 2) для геометрического представления магнитного поля используются магнитные силовые линии (для экспериментального изображения магнитных силовых линий используют металлические опилки, насыпанные на лист бумаги, в магнитном поле эти опилки выстраиваются вдоль силовых линий).
Замечание. Наряду с понятием векторной линией, часто используется также и понятие векторной трубки. Векторной трубкой называется поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой, не совпадающей (даже частично) с какой-либо векторной линией.
В вопросах, связанных с изучением полей важную роль играет задача о нахождении векторной линии поля , проходящей через заданную точку M. Пусть уравнение векторной линии имеет вид
или в векторной форме
По условию в каждой точке этой линии вектор поля направлен по касательной к ней. Из геометрического смысла производной известно, что производная любой функции определяет направление касательной к этой функции. Поэтому, производная направлена по касательной к векторной линии. Следовательно, векторы и – коллинеарны. Два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны. В результате получаем
Это есть система дифференциальных уравнений для нахождения уравнений векторных линий.
Пример 1.2. Найти уравнение векторных линий векторного поля
Решение. Для двухмерных полей система дифференциальных уравнений векторных линий принимает вид
В данном случае ; . Поэтому
Разделяя переменные и интегрируя, получим
Таким образом, векторные линии представляют собой совокупность окружностей (см. рис. 1.2).
Математическая теория поля занимается изучением его свойств, отвлекаясь от его конкретного физического смысла. Поэтому получаемое в этой теории понятие и закономерности относятся ко всем конкретным полям.
Полем называется совокупность значений той или иной величины (скорость, плотность, давление и т.п.), заданных в каждой точке рассматриваемой области.
Если рассматриваемая величина
а) скаляр , то поле называется скалярным, например

– поле плотности
б) вектор , то поле называется векторным

– поле скоростей
в) тензор , то поле называется тензорным

– поле напряжений.

Если значения рассматриваемых величин не изменяются во времени , то поле называется стационарным (установившимся), если же они изменяются во времени , то поле называется нестационарным.
Здесь мы остановимся на рассмотрении свойств стационарных полей.
Характеристики скалярного поля

1) Скалярное поле характеризуется поверхностью уровня (см. рис.)
2) Градиент поля определяется как вектор, составленный из частных производных

(1)

Он направлен по нормали к поверхностям уровня и характеризует величину и направление наибыстрейшего изменения величины поля. Полный дифференциал скалярного поля можно представить в виде:

, (2)

где .

3) Производная по направлению (см. рис. 2) определяется как проекция градиента на данное направление

(3)
Частный случай: производная по нормали :

(4)
4) Частные и полные производные по времени
Рассмотрим нестационарное скалярное поле:

Скорость изменения r в фиксированной точке равна и называется частной производной (локальной производной). Пусть задана некоторая траектория в пространстве, где определено скалярное поле (рис. 3)


Скорость изменения r вдоль траектории определяется как полная производная по t от сложной функции и равна:

(5)

– конвективная производная, она связана с перемещением точки (частицы) из одной точки пространства в другую.

Характеристики векторного поля
1) Векторная линия – кривая, направление которой в каждой ее точке совпадает с направлением вектора , отвечающего этой точке (см. рис. 4)
и
– коллинеарные (параллельные) векторы и, следовательно,
|| =
= lÞ= l

(6)
2) Производная от вектора по направлению определяется следующим образом:

(7)
– направляющие косинусы вектора , в декартовой системе координат.
Доказательство :


и так далее, подставим в , получим:


+

+

Итак, мы доказали

.
3) Частная и полная производные по времени от вектора

(9)
Доказательство :



4) Поток вектора через поверхность. Дивергенция

– поток векторной величины через элементарную площадку (элементарный поток)

(11)
векторный поток через незамкнутую площадку;

(12)
поток вектора через замкнутую площадку.

–
поток вектора скорости через поверхность S равен объему жидкости, протекающей через эту площадку поверхности за единицу времени.
По теореме Остроградского-Гаусса (рис. 7)

(13)
Сжимая объем и, следовательно получим, используя теорему осреднения

(14)

Следовательно, можно определить как предел

(15)

В гидродинамике поле скоростей имеет

дивергенция равна количеству жидкости, рассчитанному на единицу объема, вытекающему из данной точки пространства за одну секунду, т.е. равна мощности источника жидкости (если > 0).
Теория поля является разделом математики, однако понятие поля лежит в основе многих представлений современной физики. В общем случае говорят, что в пространстве задано поле некоторой величины u , если в каждой точке пространства (или некоторой его части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать несколько полей: температурное поле (в каждой точке температура имеет определённое значение), поле давлений, поле скоростей и другие поля.
Поле величины u называется стационарным, (или установившимся), если u не зависит от времени t . В противном случае поле называется нестационарным (или неустановившимся). Таким образом, величина u есть функция точки M и времени t .
В задачах физики чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные.
Скалярное поле: определение, поверхности уровня и линии уровня
Пусть D - некоторая область на плоскости или в пространстве.
Определение скалярного поля. Если в области D каждой точке M(x,y,z) пространства или точке M(x,y) плоскости в каждый момент времени t по определённому закону ставится в соответствие значение скалярной величины u , то функция u(x,y,z,t) в случае пространства или u(x,y,t) в случае плоскости называется скалярным полем.
Понятия скалярного поля и функции, определённой в области D , совпадают.
Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику тепла, температура выше, чем в точках, расположенных дальше от источника тепла. Можно привести и такие примеры, как поле освещённости, поле плотности массы и тому подобные.
Для получения более полного представления о скалярном поле используется его графическое изображение - поверхности уровня в пространстве и линии уровня на плоскости.
Линии уровня широко используются при составлении топографических и метеорологических карт. На топографических картах линия уровня - линия, в точках которой отмечена одна и та же высота над уровнем моря. На метеорологических картах строят два вида линий уровня - изотермы (линии одинаковой температуры) и изобары (линии одинакового давления).
Определение. Поверхностью уровня скалярного поля называется множество всех тех точек пространства, в которых скалярное поле постоянно.
Уравнение поверхности уровня скалярного поля u(x,y,z) :
При постоянном изменении значения C поверхности уровня заполняют всю область пространства. Если поверхности уровня размещены плотно, скалярное поле изменяется быстро. Если же поверхности уровня расположены редко, скалярное поле изменяется медленно.
Определение. Линией уровня скалярного поля называется множество всех тех точек на плоскости, в которых скалярное поле постоянно.
Уравнение линии уровня скалярного поля u(x,y) :
Пример 1. Определить поверхности уровня скалярного поля и их вид.
Решение. Уравнением поверхностей уровня данного скалярного поля является

Поверхностями уровня являются конусы с вершиной в начале координат и осью вращения Oy . Так как по области определения , то одновременно не может быть x = 0 и z = 0 . Поэтому следует исключить вершину конусов.
Пример 2. Определить линии уровня скалярного поля и их вид.
Решение. Уравнением линий уровня данного скалярного поля является
Из этого уравнения выразим "игрек":
Так как arcsinC - также константа, обозначим её C 1 . Тогда

Графиками этих линий являются параболы с вершиной в точках и ветвями вниз. На рисунке изображены линии уровня в трёх случаях: C 1 = 1 - красная линия, C 1 = 2 - зелёная линия, C 1 = 3 - синяя линия.
Векторное поле: определение, векторные линии
Понятие векторного поля во многом аналогично понятию скалярного поля.
Определение векторного поля. Если в некоторой области пространства каждой точке M по определённому закону ставится в соответствие вектор , то векторная функция называется полем вектора или векторным полем.
Таким образом, векторным полем является векторная функция точки пространства
Примерами векторного поля являются поля скорости и ускорения в текущей жидкости или газе, поле силы гравитации, поле интенсивности электростатического поля и тому подобные. Вообще, примером векторного поля может служить поле сил любой природы.
Мы будем рассматривать только стационарные векторные поля, то есть поля, не зависящие от времени.
Проекции вектора , соответствующего точке M , на координатные оси обозначим P = P(x,y,z) , Q = Q(x,y,z) , R = R(x,y,z) . Тогда векторное поле сможем задать через компоненты:
Таким образом, векторное поле можно определить тремя скалярными функциями P , Q , R . Пусть эти функции и их частные производные по переменным x,y,z являются непрерывными функциями.
Определение. Векторной линией называется линия, направление которой в каждой точке касательной совпадает с направлением вектора поля в этой точке (рисунок ниже).

Векторные линии поля силы обычно называют линиями силы, векторные линии поля скоростей потока жидкости или газа - векторами потока. У стационарного потока жидкости линии потока совпадают с траекториями частиц жидкости.
Уравнения векторных линий можно найти, решив систему дифференциальных уравнений
Известная также, как векторный анализ. А кому-то векторный анализ, известный как теория поля =) Наконец-то мы добрались до этой интереснейшей темы! Данный раздел высшей математики язык не поворачивается назвать простым, однако ж, в грядущих статьях я постараюсь достигнуть двух целей:
а) чтобы все понимали, о чём вообще идёт разговор;
Весь материал будет изложен в популярном стиле, и если вам нужна более строгая и полная информация, то можно взять, например, 3-й том Фихтенгольца или заглянуть в Вики.
Поле с травой, футбольное поле…. Ещё? Поле деятельности, поле экспериментов. Приветствую гуманитариев! …Из школьного курса? Электрическое поле, магнитное, электромагнитное…, так, хорошо. Гравитационное поле Земли, в котором мы находимся. Отлично! Так, кто это там сказал о поле действительных и комплексных чисел? …совсем какие-то монстры здесь собрались! =) Благо, алгебра уже пройдена.
На ближайших уроках мы познакомимся со специфическим понятием поля, конкретными примерами из жизни, а также научимся решать тематические задачи векторного анализа. Теорию поля лучше всего изучать, как вы правильно догадываетесь, на поле – природе, где есть лес, речка, озеро, деревенский домик, и я приглашаю всех погрузиться если и не в тёплую летнюю реальность, то в приятные воспоминания:
Во-первых, скаляр. Довольно-таки часто этот термин ошибочно отождествляют с числом. Нет, всё обстоит немного не так: скаляр – это величина, каждое значение которой может быть выражено лишь одним числом. В физике примеров масса: длина, ширина, площадь, объём, плотность, температура и др. Всё это скалярные величины. И, кстати, масса – тоже пример.
Во-вторых, вектор. Алгебраического определения вектора я коснулся на уроке о линейных преобразованиях и одну из его частных ипостасей не знать просто невозможно =) Типичный вектор выражается двумя или бОльшим количеством чисел (своими координатами). И даже для одномерного вектора лишь одного числа не достаточно – по той причине, что у вектора есть ещё направление. И точка приложения, если вектор не свободен. Векторами характеризуют силовые физические поля, скорость и многие другие величины.
Ну что же, теперь можно приступить к сбору алюминиевых огурцов урожая:
Скалярное поле
Если каждой точке некоторой области пространства поставлено в соответствие определённое число (чаще действительное), то говорят, что в этой области задано скалярное поле.
Рассмотрим, например, исходящий из земли перпендикулярный луч. Воткните для наглядности лопату =) Какие скалярные поля можно задать на этом луче? Первое, что напрашивается – это поле высоты – когда каждой точке луча поставлена в соответствие её высота над уровнем земли. Или, например, поле атмосферного давления – здесь каждой точке луча соответствует числовое значение атмосферного давления в данной точке.
Важнейшим свойством скалярного поля является его инвариантность относительно системы координат. Если перевести на человеческий язык, то с какой бы стороны мы на лопату / озеро ни посмотрели – скалярное поле (высота, глубина, температура и т.д.) от этого не изменятся. Более того, скалярное поле, скажем, глубины можно ведь задать и на другой поверхности, например, на подходящей полусфере, или непосредственно на самой водной поверхности. А почему нет? Разве нельзя каждой точке полусферы, расположенной над озером, поставить в соответствие число? Плоскость я предложил исключительно ради удобства.
Добавим ещё одну координату. Возьмите в руку камень. Каждой точке этого камня можно поставить в соответствие его физическую плотность. И опять – в какой бы системе координат мы его ни рассмотрели, как бы ни крутили в руке – скалярное поле плотности останется неизменным. Впрочем, некоторые люди могут оспорить этот факт =) Такой вот философский камень.
Надо сказать, ловким получился переход к следующему параграфу:
Векторное поле
Если каждой точке некоторой области пространства поставлен в соответствие вектор с началом в данной точке, то говорят, что в этой области задано векторное поле.
Большую группу векторных полей образуют так называемые поля скоростей. Посмотрите на поле (которое с травкой) и мысленно очертите над ним произвольную пространственную область. Представьте, что над полем дует ветер – небольшой такой ураганчик для пущей наглядности. Теперь зафиксируем некоторый момент времени и каждой точке построенной области поставим в соответствие несвободный вектор, который характеризует:
а) направление движения воздуха в данной точке;
б) и скорость его движения в данной точке – чем выше скорость, тем длиннее вектор. Если в какой-то точке штиль, то ей сопоставляется нулевой вектор.
Множество этих векторов и образует векторное поле скорости ветра в данный момент времени.
Аналогично устроено поле скоростей течения жидкости – так, например, каждой точке реки в некоторый момент времени можно поставить в соответствие вектор, указывающий направление и скорость течения жидкости в этой точке.
Да чего там ветер и река, поле скорости можно смоделировать собственноручно, для этого достаточно взмахнуть рукой. Или даже моргнуть глазом.
* Далее по умолчанию считаем, что все дела происходят в декартовой системе координат
! Обозначения: векторные поля также обозначают буквой либо , а их компоненты через либо соответственно.
Из вышесказанного давно и очевидно следует, что, по меньшей мере математически, скалярные и векторные поля можно определить и во всём пространстве. Однако с соответствующими физическими примерами я всё же поостерёгся, поскольку таких понятий, как температура, гравитация (или других) ведь где-то может и вовсе не существовать. Но это уже не ужасы, а научная фантастика =) И не только фантастика. Ибо внутри камней ветер, как правило, не дует.
Векторные линии
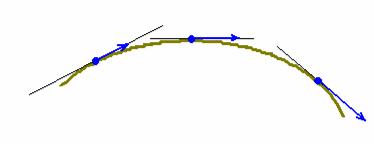
Постараюсь сформулировать попроще: каждая точка векторной линии является началом вектора поля, который лежит на касательной в данной точке:
Разумеется, векторы линии в общем случае имеют разную длину, так на приведённом рисунке, при перемещении слева направо их длина растёт – здесь можно предположить, что мы приближаемся, например, к магниту. В силовых физических полях векторные линии так и называют – силовыми линиями. Другой, более простой пример – это гравитационное поле Земли: его силовые линии представляют собой лучи с началом в центре планеты, причём векторы силы тяжести расположены прямо на самих лучах.
Векторные линии скоростных полей называются линями тока. Множество линий тока даёт нам представление о потоке жидкости или газа в данный момент времени. К слову, линия тока и траектория движения частицы – это не одно и то же. Если поле скоростей не меняется с течением времени (например, река с устоявшимся течением), то, да – мусоринки будут плыть по линиям тока. Такое поле называют стационарным, и в нём траектории движения частиц совпадают с линиями тока. Но представьте пыльную бурю – здесь линии тока в каждый момент разные, и поэтому мусоринка будет лететь по своей уникальной траектории, а вовсе не по какой-то конкретной линии тока.
Вообще, многие понятия теории поля пришли из гидродинамики, с чем мы ещё не раз столкнёмся.
если , то нужно решить систему ;
если , то систему ;
и если , то .
И что-то непозволительно давно у нас не было практики:
Найти силовые линии векторного поля
Решение: в данной задаче , поэтому решаем систему:
Первый диффур вообще халява:
– семейство плоскостей, параллельных координатной плоскости (представили в уме!).
Второй диффур – почти она же:), ну а зачем нам скоропостижные трудности?
– семейство (внимание!) параболических цилиндров, параллельных оси .
Ответ: искомое множество векторных линий:
Аналогичная задачка для самостоятельного решения:
Найти силовые линии векторного поля
Охарактеризуйте получившееся множество линий. Кстати, в условии явно не сказано, о каком поле идёт речь – плоском или пространственном. В подобных ситуациях рекомендую решать задачу для пространства – не ошибётесь ;-)
Краткое решение и ответ в конце урока.
Векторное поле градиентов
В каких отношениях вы находитесь с производной по направлению и градиентом? …ничего страшного, от ненависти до любви – один шаг =) Напоминаю, что градиент функции в точке – это несвободный вектор, указывающий направление максимального роста функции в данной точке и определяющий скорость этого роста.
Нахождение векторной функции градиентов – есть популярный и распространённый способ получить из скалярного поля поле векторное. При условии существования соответствующих частных производных функции двух и трёх переменных:
Смысл очень прост. Так, если функция задаёт скалярное поле глубины озера, то соответствующая векторная функция определяет множество несвободных векторов, каждый из которых указывает направление наискорейшего подъёма дна в той или иной точке и скорость этого подъёма.
Если функция задаёт скалярное поле температуры некоторой области пространства, то соответствующее векторное поле характеризует направление и скорость наибыстрейшего прогревания пространства в каждой точке этой области.
Разберём общую математическую задачу:
Дано скалярное поле и точка . Требуется:
1) составить градиентную функцию скалярного поля;
2) найти градиент поля в точке и вычислить его длину;
3) вычислить производную по направлению нормального вектора к поверхности в точке , образующего с положительной полуосью тупой угол.
Непосредственно к решению задачи это не относится, но сразу обратим внимание, что скалярное поле не определено на всех трёх координатных плоскостях .
1) Быстренько вспоминаем, как находить частные производные функции трёх переменных:
Составим функцию, которая определяет векторное поле градиентов:
И ещё раз – в чём её смысл? Полученная векторная функция каждой точке области определения скалярного поля ставит в соответствие вектор , указывающий направление и максимальную скорость роста функции в данной точке.
И один из таких векторов нам предстоит найти в следующем пункте:
2) Вычислим частные производные в точке :
Мерилом же этой максимальной скорости как раз является длина градиента:
3) Вычислим производную по направлению нормального вектора к поверхности в точке , образующего с положительной полуосью тупой угол.
Получено верное равенство. ОК.
Что это за поверхность – нас не интересует, нам важен её нормальный вектор в точке , да не абы какой, а образующий с полуосью тупой угол.
Вспоминаем материал ещё одного урока: вектор нормали к поверхности в точке задаётся следующим образом:
В данном случае:
, следовательно, угол между этими векторами острый, что нас не устраивает!
И поэтому нужно выбрать противоположно направленный нормальный вектор:
Заметим заодно, что нормальные векторы в отличие от градиентов – свободны, их задача лишь указать направление.
Вычислим направляющие косинусы данного направления, или, что то же самое – координаты единичного вектора, сонаправленного с вектором :
Таким образом, искомая производная по направлению:
Напоминаю, что это значение характеризует скорость роста функции в точке по направлению вектора , и оно не может оказаться больше, чем (максимальной скорости роста в данной точке).
Ответ:
Небольшой пример для самостоятельного решения:
Найти угол между градиентами скалярных полей и в точке
Потенциальное векторное поле
В физике есть конкретная математическая модель, описывающая гравитационные силы, но в соответствии с направленностью сайта, я приведу только общие формулы. Итак:
Векторное поле является потенциальным, если оно представляет собой поле градиентов некоторого скалярного поля . Функцию называют потенциальной функцией или просто потенциалом.
Работа потенциального векторного поля по перемещению материальной точки из точки в точку не зависит от траектории её движения и выражается следующим криволинейным интегралом 2-го рода:
, который равен разности потенциалов .
Иными словами, в потенциальном поле имеет значение лишь начальная и конечная точка маршрута. И если эти точки совпадают, то суммарная работа сил по замкнутому контуру будет равна нулю:
Давайте поднимем пёрышко с земли и доставим его в исходную точку. При этом траектория нашего движения опять же произвольная; можно даже бросить перо, снова его поднять и т.д.
Почему итоговый результат нулевой?
Таким образом, суммарная работа сил равна нулю:
Как я уже отмечал, физическое и обывательское понятие работы отличаются. И это различие вам хорошо поможет понять не пёрышко и даже не кирпич, а, например, пианино :)
Дружно поднимите пианино и спустите его по лестнице вниз. Потаскайте по улице. Сколько захочется и где захочется. И если никто не вызвал дурку занесите инструмент обратно. Вы поработали? Конечно. До седьмого пота. Но с точки зрения физики никакой работы не совершено.
Ротор векторного поля
Или его вихревая составляющая, которая тоже выражается векторами.
Снова возьмём в руки пёрышко и аккуратно отправим его в плавание по реке. Для чистоты эксперимента будем считать, что оно однородно и симметрично относительно своего центра. Ось торчит вверх.
Рассмотрим векторное поле скорости течения (считаем, что оно неизменно во времени), и некоторую точку водной поверхности, над которой находится центр пера.
Если векторное поле задано функцией , то его роторное поле задаётся следующей векторной функцией:
И, наконец, отвечаем на поставленный выше вопрос: в любой точке потенциального поля его ротор равен нулю:
, а точнее, нулевому вектору.
Потенциальное поле также называют безвихревым полем.
После чего с чистой совестью и повышенным тонусом можно вернуться к практическим задачам:
Показать, что векторное поле является потенциальным и найти его потенциал
Решение: условие прямо утверждает потенциальность поля, и наша задача состоит в доказательстве этого факта. Найдём роторную функцию или, как чаще говорят – ротор данного поля:
Для удобства выпишем компоненты поля:
Таким образом:
, следовательно, поле потенциально, а значит, представляет собой градиентную функцию некоторого скалярного поля, заданного потенциалом .
Функцию обычно находят одним из следующих способов:
1) Способ первый. Коль скоро так (см. выше), то:
Дальнейший алгоритм напоминает решение дифференциального уравнения в полных дифференциалах, только с бОльшим количеством шагов:
Но, с другой стороны . Приравниваем и упрощаем:
Но с другой стороны, . Приравниваем и упрощаем:
– получаем тем самым, искомую потенциальную функцию.
Проверку тут выполнить легче лёгкого, находим частные производные 1-го порядка:
которые совпали с соответствующими компонентами исходного поля , в чём и требовалось убедиться.
2) Способ второй. Потенциальную функцию можно найти при помощи формулы:
, где – точка с переменными координатами, а – некоторая фиксированная точка скалярного поля .
Легко видеть, что этот криволинейный интеграл определяет работу векторного поля от точки до точки и численно равен разности потенциалов , откуда, собственно, и получается нужная функция
Запишем сумму трёх интегралов для поля :
И на этом шаге я по возможности рекомендую выбрать точку (если функция и её производные в ней определены). После чего решение значительно упрощается:
Ответ:
Если начало координат выбрать нельзя, то задачу придётся решать в общем виде, в результате чего должна получиться разность . Любители трудностей могут вернуться к примеру и прийти к разности . Разумеется, это легальный и рабочий вариант – можно решать и так.
Пара полей для самостоятельного решения:
Выяснить, является ли следующие векторные поля потенциальными, и если да, то найти их потенциалы:
Обязано ли поле быть потенциальным в таких задачах? Конечно, нет, и отрицательный ответ – это тоже полноценный ответ. Примерный образец чистового оформления заданий внизу страницы.
Ну что же, теперь пришло время немного отдохнуть и увеличить ротор реки =) А именно нырнуть, искупаться и позагорать на солнце. Чтобы с новыми силами вернуться к столь увлекательной теме, а именно к потоку и циркуляции векторного поля
Спасибо за внимание и до скорых встреч!
Решения и ответы:
Пример 2: Решение: составим и решим систему:
Из 1-го уравнения:
Из 2-го уравнения:
Константу переобозначим через
Ответ: – семейства эллипсов, расположенные в плоскостях , параллельных плоскости .
Пример 4: Решение: вычислим частные производные функции в точке :
Составим градиент данного скалярного поля в точке и вычислим его длину:
Аналогично найдём градиент второго скалярного поля:
В результате:
Угол между градиентами найдём по формуле:
Таким образом:
Пример 6: Решение:
а) проверим, равен ли нулю ротор векторного поля:
.
В данном случае:
Следовательно,
Ответ: поле не потенциально.
Ответ: поле потенциально,
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Читайте также:

