Скорости и ускорения точек вращающегося тела реферат

Обновлено: 04.07.2024

Тело вращается вокруг точки О. Определим параметры дви­жения точки А, расположенной на расстоянии r _а от оси вращения (рис. 11.6, 11.7).

Путь точки A: S_A = ωr_А

Линейная скорость точки A: v_A = ωr_А

Ускорения точки A: a_tA = εr_А — касательное;

а_пA = ω 2 r_А — нормальное, где r_А — радиус окружности, траектории точки А.

Примеры решения задач

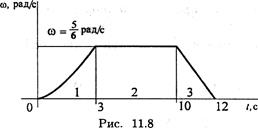
Пример 1. По заданному графику угловой скорости (рис.11.8)определить вид вращательного движения.

Решение

1. Участок 1 — неравномерное ускоренное движение,

ω = φ / ; е = ω / .

2. Участок 2 — скорость постоянна — движение равномерное, ω = const.

3. Участок 3 — скорость убывает равномерно — равнозамедленное движение, е = ω /

Число оборотов за 30 с:

2. Определяем время до полной остановки.

Скорость при остановке равна нулю, ω = 0.

Таким образом, ω = ω₀ + et 0 = ω₀ + et

Пример 5. Маховое колесо вращается равномерно со скоро­стью 120 об/мин (рис. 11.10). Радиус колеса 0,3 м. Определить ско­рость и полное ускорение точек на ободе колеса, а также скорость точки, находящейся на расстоянии 0,15 м от центра.

Решение

Касательное ускорение точки A a_tA = 0; нормальное ускорение точки А а_nA = ω 2 r_A

а_пA = (12,56) 2 • 0,3 = 47,3м/с 2 . 5. Полное ускорение точек на ободе колеса

Пример 6. Точка начала двигаться равноускорено по прямой из состояния покоя и через 25 с ее скорость стала равна 50 м/с. С этого момента точка начала равнозамедленное движение по дуге окружности радиуса г = 200 м и через 20 с ее скорость снизилась до 10 м/с. После этого точка продолжила свое движение с этой скоростью по прямой и через 5 с внезапно остановилась.

Определить: 1) среднюю скорость точки на всем пути;

2) полное ускорение точки через 10 с после начала ее равнозамедленного движе­ния по окружности.

Решение

1. Представим траекторию движения точки, как пока­зано на рис. 5. Весь путь, пройденный точкой, разбиваем на участки равноускоренного (по отрезку АВ), равнозамедленного (по дуге ВС) и равномерного (по отрезку CD) движения.

2. Рассмотрим движения точки по отрезку АВ:

3. Рассмотрим движение точки по дуге ВС:

4. Рассмотрим движение точки на отрезке CD:

5. Определим среднюю скорость точки на всем пути по траектории движения ABCD (см. рис. 5):

t_ABCD = t_AB + t_BC + t_CD = 25 + 20 + 5 = 50 c

6. Определим значение полного ускорения точки через 5 с после начала равнозамедленного движения (см. положение К на рис. 5)

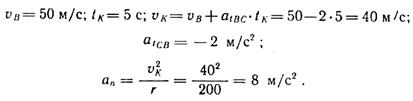
Пример 7.Тело начало вращаться из состояния покоя и через 15 с его угловая скорость достигла 30 рад/с. С этой угловой скоростью тело вращалось 10 с равномерно, а затем стало вращаться равнозамедленно в течение 5 с до полной остановки.

1) число оборотов и среднюю угловую скорость тела за все время вращения;

2) окружную скорость точек тела, расположен­ных на расстоянии r = 0,5 м от оси вращения тела через 5 с после начала движения.

Решение

1. Разграничим вращательное движение данного тела на участки равноускоренного, равномерного и равнозамедленного дви­жения. Определим параметры вращательного движения тела по этим участкам.

2. Равноускоренное вращение (участок 1):

3. Равномерное вращение (участок II):

4. Равнозамедленное вращение (участок III):

5. Определим полное число оборотов тела за все время вращения:

6. Определим среднюю угловую скорость тела за все время враще­ния:

7. Определим окружную скорость точек тела, расположенных на расстоянии r = 0,5 м от оси вращения через 5 с после начала движения тела:

Пример 8. Диск радиусом R = 2 м вращается вокруг неподвижной оси согласно уравнению

(φ — в радианах, t — в секундах). Определить скорость и ускорение точки поверхности диска в моменты времени t₁ = 0 и t₂ = 2 с.

Решение

Для определения скорости и ускорения точки необходимо знать угловую скорость и угловое ускорение диска.

Уравнение изменения угловой скорости диска:

Уравнение изменения углового ускорения диска:

Определим угловую скорость и угловое ускорение диска в моменты времени t₁ = 0 и t₂ = 2 с:

Определим скорость точки поверхности диска в ука­занные моменты времени:

Определим нормальное и касательное ускорения точки поверхности диска в моменты времениt₁ и t₂:

Пример 9. Точка А, лежащая на ободе равно­мерно вращающегося шкива, движется со скоростью v = 2 м/с и нормальным ускоре­нием а_п = 5 м/с 2 . Определить ра­диус шкива OA и величину угло­вой скорости (рис. 1.46).

Решение

Здесь для решения следует воспользоваться известны­ми соотношениями для линейной скорости и нормального ускорения точек вращающегося тела:

Если второе уравнение разделить на первое, найдем угловую скорость вращения шкива:

Пример 10. Шарик А (рис. 1.47), подвешенный на стержне OA, колеблется в вертикальной плоскости около неподвижной горизонтальной оси О согласно уравнению

(φ — в радианах, t — в секундах).

1. Ближайшие моменты времени, соответствующие максимальным отклонениям стержня OA от вертикали OC вправо и влево, а также значение максимальных углов отклонения.

2. Ближайший момент времени после начала движе­ния, при котором нормальное ускорение шарика равно нулю.

3. Ближайший момент времени, при котором касатель­ное ускорение шарика равно нулю.

4. Полное ускорение шарика при t = 1,5 с и угол, образованный вектором ускорения со стержнем OA.

Решение

Стер­жень OA совершает вращательное (коле­бательное) движение. Максимальные углы отклонения стержня от вертикали соот­ветствуют наиболь­шим абсолютным значениям функции sin (πt/6). Очевидно, это имеет место при sin (πt/6) = ± 1:

При t₁ = 3 с φ_тах = π/4, при t₂ = 9 с φ_тах = -- π/4.

Крайние положения стержня OA на рис. 1.47 пока­заны штриховыми линиями OA₁ и ОА₂.

Напомним, что за положительное направление считаем вращение по часовой стрелке.

Уравнение изменения угловой скорости стержня OA

Уравнение изменения углового ускорения стержня OA

Направления ω и ε показаны на рис. 1.47. В приве­денном примере направления ω и ε противоположны. Следовательно, стержень OA совершает замедленное вра­щательное движение.

Нормальное и касательное ускорения шарика опреде­ляются по формулам:

В рассматриваемом примере касательное ускорение шари­ка направлено к точке С (рис. 1.47).

Определим момент времени, при котором а_п равно нулю. Для этого выражение а_п приравняем нулю:

Записанное условие выполняется при

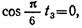
Нормальное ускорение шарика равно нулю, когда стержень OA занимает крайние положения.

Определим момент времени, при котором a_t равно нулю. Для этого выражение a_t приравняем нулю:

Это условие выполняется при

Касательное ускорение шарика обращается в ноль в тот момент, когда стержень OA совпадает с линией OC. Вычислим а_n и a_t при t = 1,5 с:

Ускорение шарика при t = 1,5 с

Угол между вектором ускорения шарика и стержнем OA определяется из соотношения

Пример 11. Через 30 с равномерного вращательного движения с частотой n₀ = 600 об/мин тело начало равнозамедленное движение и в течение последую­щих 20 с частота вращения тела уменьшилась до n = 450 об/мин.

Определить угловое ускорение тела при равнозамедленном вращательном движении, а также количество оборотов тела за время равномерного и равнозамедленного движения.

Решение

1. Переведем начальную и конечную частоты вращения тела в еди­ницы угловой скорости:

2. За время t₁ = 30 с тело, вращаясь равномерно с угловой скоростью ω₀ = 20π рад/с, повернулось на угол

3. По формуле угловое ускорение, с которым тело вращалось в те­чение времени t₂ = 20 с

4. За время равнозамедленного движения тело повернулось на угол

5. За весь промежуток времени t₁ + t₂ = 50 с тело повернулось на угол

следовательно, тело сделало

Для определения количества оборотов, сделанных телом, можно было частоту вращения и не переводить в единицы угловой скорости. За время t₁ = 30 с = 0,5 мин при равномерном движении тело сделало

За время t₂ = 20 с = 1/3 мин при равнозамедленном вращении тело сделало

Контрольные вопросы и задания

1. Какими кинематическими параметрами характеризуется по­ступательное движение и почему?

2. Запишите уравнение равномерного поступательного движе­ния твердого тела.

3. Запишите уравнение равнопеременного поступательного дви­жения твердого тела.

4. Запишите уравнения равномерного и равнопеременного вра­щательного движений твердого тела.

5. Задано уравнение движения тела S = f(t). Как определяют скорость и ускорение?

6. Для заданного закона (уравнения) движения

φ = 6,28 + 12t + 3t 2 выберите соответствующий кинематический график движения (рис. 11.11).

7. Для движения, закон которого задан в вопросе 6, определите угловое ускорение в момент t = 5 с.

Линейные скорости и ускорения точек вращающегося тела

• Линейная скорость и ускорение точки ротатора-произвольная точка ротатора на расстоянии R от оси вращения, описывающая окружность радиуса/?. Центр этого круга находится на оси вращения, а плоскость, на которой он расположен, Q, перпендикулярна оси вращения(рис. 11.5). Скорость и ускорение любой точки

вращающегося тела называют линейными. Для их определения достаточно одной точки М(рис. 11.5). Как уже указывалось, траектория его движения представляет собой дугу окружности. В первый момент точка м находится в положении Л40, и время с позиции Афи. Возьмем начало координат в точке Mo,

Например. Шестерня / Шестерня 2 (Рис. 11.7) из оставшегося состояния начинает вращаться равномерно ускоренно с угловым ускорением 81=0,1 Радиана / сек. Решение. Так как начальная угловая скорость первой передачи равна нулю(Oi=ei/+0, l-T. Закон равного вращения первой шестерни равен= Людмила Фирмаль

последнего уравнения, то получим закон вращения шестерни 2\CP2=f в первый раз(P2=0,15/(// = 0,15-/2/2-=0,075/2. б Вращение 104-й шестерни равномерно ускоряется, как видно из законов движения. В этом случае тангенциальное ускорение E2=2(p2l2= = 0,075 -2/2//2=0,15 Радиан / С2. Найти линейную скорость точки N: Y нет. (O2/?л=0.15/-0.1= = 0.015/. Суммарный коэффициент ускорения для точки N=e24′(Y1= = 0,11/ 0,152+(0,150 4 = 0,015 К1 + 0,0225/. Следует отметить, что в точке контакта м только линейное ускорение колеса остается одинаковым, а линейное нормальное и полное ускорения различны(рис. 11.8). Итак, в нашем случае знание- 105чения тангенциального

Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Если тело вращается вокруг оси, то его точки перемещаются по окружностям (рис. а), радиусы которых г равны расстоя­ниям точек от оси вращения.

Рассмотрим точку М, которая за время dt прошла путь ds = ММ₁. В данном случае путь ds можно определить как произве­дение угла поворота на радиус окружности, т. е.

Линейная скорость определится как производная пути по вре­мени

Подставив вместо ds его значение по (10), получим

v = ds/dt = d(rφ)/dt = r_* dφ/dt = rω11

Подставив в формулу для линейной скорости точек тела, вра­щающегося вокруг неподвижной оси, значение частоты вращения в оборотах в минуту (об/мин), получим

v = r =

Касательное ускорение точки вращающегося тела определяется из выражения

a_t = dv/dt = d(rω)/dt = r _* dω/dt = rε

Нормальное ускорение точки равно отношению квадрата ско­рости к радиусу окружности

Пример7. Скорость точки за 15 с. возрастает от 20 км/ч до 80 км/ч. Определить какой путь пройдет точка за время разгона и каково будет ее ускорение в конце 15 – ой секунды если движение происходит по дуге r = 50 м.

v₀ = 20 км/ч = 5,6 м/с

v₁ = 80 км/ч = 22,3 м/с R

a_t = v – v₀ /t = 22,3 – 5,6 /15 = 1,12 м/с

а_п = v 2 /r = 22,3 2 / 50 = 10 м/с 2

a = 2 _t +a 2 _n = √1,12 2 + 10 2 = √1,25 + 100 = 10м/с 2

Пример 8. Автомобиль движется со скоростью v = 54 км/ч при торможении он получает замедление a_t = - 0,5 м/с 2 . Найти какой путь он прошел от начала торможения до полной остановке и сколько времени продолжалось торможение.

Определить S;t

t = v – v₀ / a_t = 0-15 / -0,5 = 30 c

Пример 9. На пути 600 м скорость точки уменьшается с 30 до 10 м/с. Определить время этого движения, а также полное ускорение в начале и в конце движения если точка двигалась по дуге r = 400м.

t = 2S / v₀ + v₁ = 2 _* 600 / 30+10 = 30c

а_п1 = v ₀ 2 /r = 30 2 /400 = 2,25 м/с 2

a₁ = 2 _t1 +a 2 _n1 = √ -0,67 2 + 2,25 2 = √0,45 + 5,062 = 2,35 м/с 2

а_п2 = v ₁ 2 /r = 10 2 /400=0,25м/с 2

a₂ = 2 _t2 +a 2 _n2 = √ -0,67 2 + 0,25 2 = √0,45 + 0,062 = 0,715 м/с 2

Пример 10. Точка начала прямолинейное равноускоренное движение из состояния покоя и ч/з 5сек приобрела скорость 10 м/с с этого момента точка стала двигаться равномерно по окружности r = 10 м, ч/з 15 сек движение по окружности точка внезапно остановилась. Определить: 1. Путь пройденный точкой за все время движения; 2. Среднюю скорость на этом пути; 3. Ускорение точки на прямолинейном и криволинейном участке пути.

S = S₁ + S₂ = 25 + 150 = 175 м

v_ср = S / t₁ + t₂ = 175 / 20 = 8,75 м/с = 8,75 _* 3,6 = 31,5 км /ч

a_n = v₂ / r = 10 2 / 10 = 100 / 10 = 10 м/с

Пример 11. Автомобиль, имея начальную скорость 72 км/ч проходит за 20 сек путь 600 . Найти скорость и ускорение (полное) в конце 20 сек, считая движение равнопеременным по дуге окружности радиуса r = 1200 м

v₀ = 72 км/ч= 20 м/с

Определить v; a

v = 2S / t – v₀ = 2 _* 600 / 20 – 20 = 40м/с

a_t = v – v₀ /t = 40 – 20 / 20 = 1 м/с 2

а_п = v 2 /r = 40 2 / 1200 = 1,3 м/с 2

а = √а_t 2 + a_n 2 = √1 2 + 1,3 2 = 1,6 м/с 2

Пример 12. Точка прошла за время 20 сек с касательным ускорением a_t = 4 м/с 2 путь 1400 м по дуге r = 100 м. Определить v₀ , а

S = 1400 м r

S = v_{0 *} t + a_{t *} t 2 / 2 =>v₀ = S - a_{t *} t 2 / 2 _/t = 1400 – 4_* 20 2 _/20 = 30м/с

а_п = v 2 /r = 110 2 / 100 = 121 м/с 2

а = √а_t 2 + a_n 2 = √121 2 + 4 2 = 121,1м/с 2

Пример 1. Равномерно вращающееся тело делает 10800 оборотов в час. Определить его угловую скорость.

n = 10800 об/час = 10/800 : 60 = 180 об/мин ω = π _* n / 30 = 6 π рад / сек

___________

Пример 2. Угловая скорость равномерно вращающегося тела ω = 8 рад / сек. Определить сколько оборотов в час делает тело.

ω = 8 рад / сек

__________ ω = π _* n / 30 => n = 30 _* ω / π=76,4 об/мин = 60 _* 76,4 = 4585 об/ч

Пример 3. Расстояние от Луны до Земли рано 384000 км. Найти скорость движения Луны по своей орбите, если полный оборот около Земли она совершает в 27 суток. Орбиту Луны принять за окружность, а движение считать равномерным.

Дано: 27 суток = 27 * 24 * 3600 = 2332800 сек

r = 384000 км Sкруга = π D = 2π r = 2 * 3,14 * 384000000м = 2411520000 м

t = 27 суток v = s / t = 2411520000 / 2332800 = 1034м / c

Пример 4.

r = 149600000 км – расстояние от земли до солнца

t = 365 дней = 365 _* 24 _* 3600 = 31536000 сек

v - ? – земли вокруг солнца

Sкруга = π D = 2π r = 2 _* 3,14 _* 149600000000м

v = s / t = 29791 м / сек

Пример 5. Вал, начинает вращаться равноускоренно из состояния покоя, в первые 10 сек совершает 30 оборотов. Какова его угловая скорость по истечению 5 сек?

t₁ = 10 сек φ_об = φ / 2π => φ = φ_{об *} 2π = 188,4 рад

t₂ = 5 сек φ = ω _* t / 2 => ω = 2φ / t = 2 _* 188,4 / 10 = 37,68 рад/сек(при10 сек)

___________

ω - ? ω = 37,68 / 2 = 18,84 рад / сек (при 5 сек)

Пример 6. Вал, начинает вращаться равноускоренно из состояния покоя, делает 4800 об в первые 2 мин. Найти угловое ускорение вала.

φ = 4800 об φ_об = φ / 2π => φ = φ_{об *} 2π = 4800 _* 2 _* 3,14 = 30144 рад.

t = 2 мин φ = ε _* t 2 / 2 => ε = 2φ / t 2 = 2 _* 30144 / 120 2 = 4,18 рад / сек 2

Пример 7. Колесо начинает вращаться равноускоренно из состояния покоя, Через 20 мин после начала движения колесо имело угловую скорость, соответствующую 240 об / мин. Сколько оборотов сделало колесо за эти 20 мин.

t = 20 мин φ = ω _* t / 2 = 240 * 20 / 2 = 2400 об

ω = 240 об / мин

Пример 8. Колесо, вращающееся вокруг неподвижной оси с угловой скоростью ω = 4π рад/сек, было затем отключено от привода, поддерживавшего заданную рабочую скорость вра­щения. Сделав 25 оборотов, колесо вследствие трения в под­шипниках остановилось. Полагая вращение равнозамедленным, определить угловое ускорение колеса.

ω₀ = 4π рад/с ε = ω – ω₀ / t = 0 - 4π / t = - 4π / t

φ = 25 об φ = φ_{об *} 2π = 25 * 2 * 3,14 = 157 рад

ω = 0 φ = ω + ω₀ / 2 * t = ω₀ * t / 2 => t = 2φ / ω₀ = 2 * 157 /4π = 25 сек

ε - ? ε = -4π / t = 4 * 3,14 / 25 = - 0,5 рад / сек 2

Пример 9. При посадке самолета пропеллер вращается с угло­вой скоростью, соответствующей п = 900 об/мин. После выключения мотора пропеллер сделал до остановки 60 обо­ротов. Считая вращение пропеллера после выключения мо­тора равнозамедленным, определить, сколько времени про­шло с момента выключения мотора до остановки. Опреде­лить ускорение пропеллера.

n = 900 об/мин φ_об = φ / 2π => φ = φ_{об *} 2π = 60 * 2 * 3,14 = 376,8 рад

φ = 60 об ω₀ = π n / 30 = 3,14 * 900 / 30 = 94,2 рад / сек

ω = 0 φ = ω + ω₀ / 2 _* t = 0 + ω₀ * t / 2 => t = 2φ / ω₀ = 2 * 376,8 / 94,2 = 8 сек

t - ? ε - ? ε = ω – ω₀ / t = 0 – ω₀ / t = 94,2 / 8 = 11,775 рад / сек 2

Пример 10. Маховое колесо радиуса R = 2 м вращается равно­ускоренно из состояния покоя; через t =10 сек точки, ле­жащие на ободе, обладают линейной скоростью v = 50 м/сек. Найти скорость, нормальное и касательное ускорения точек обода колеса для момента t = 25 сек.

r = 2 м v₁ = r _* ω => ω = v / r = 50 / 2 = 25 рад/сек

ω₀ = 0 ε = ω₁ / t₁ = 25 / 10 = 2,5 рад/сек 2

t_{1 =} 10 с ε = ω₂ / t₂ => ω₂ = ε * t = 2,5 * 25 = 62,5 рад / сек

t₂ = 25 с a_t = r * ε = 2 * 2,5 = 5 м/с 2

v₂ - ? a_n - ? a_t - ? a_n = v₂ 2 / r = 125 2 / 2 = 7812,5м/с 2

Пример 11. Точка пробегает в минуту 200 раз окружность, диаметр которой 3 м. Вычислить ускорение точки.

Дано: ω = π n / 30 = 3,14 * 200 / 30 = 20,9 рад/сек

n = 200 об/мин v = r * ω = 1,5 * 20,9 = 31,4 м/с

D = 3м a_n = v₂ 2 / r = 31,4 2 / 1,5 = 660м/с

Пример 12. Частота вращения маховика составляет 300 об/мин затем маховик бал заторможен и ч/з 3 с частота его вращения уменьшилась до 120 об/мин. Определить ч/з сколько времени маховик остановится и сколько оборотов он совершит от начала торможения до полной остановки.

n₀ = 300об/мин ω₀ = πn₀ / 30 = 300π / 30 = 10π рад/сек

t₁ = 3c ε = const ω₁ = πn₁/ 30 = 120π / 30 = 4π рад/сек

n₁ = 120об/мин ε = ω₁ - ω₀ / t₁ = 4π - 10π / 3 = - 2π рад/сек 2

_________ φ = ω_{ср *} t = (ω₀ + ω₂) _* t /2 = 10π _* 5 / 2 = 25π рад

t₂ - ? φ - ? φ_об = φ / 2π = 25π / 2π = 12,5 об

Пример 13. Ротор эл двигателя делает 2700 об/мин. После выключения ротор останавливается совершив 675 об. Определить время вращения ротора с момента выключения до полной остановки.

n₀ = 2700об/мин ω₀ = πn₀ / 30 = 2700π / 30 = 90π рад/сек

t₁ = 3c φ_об = φ / 2π => φ = 2π φ₀ = 2π675 = 1350 рад

ω₁ = 0 t = 2φ / ω₀ + ω₁ = 2 _* 1350 / 90π = 30с

Пример 14. Тело при вращении с постоянным угловым ускорением 24 рад/с 2 в течении 105 сек сделано 2100 об. Определить угловую скорость тела в начале и конце равнозамедленного вращения.

t = 105 сек φ = 2π φ₀ =2π _* 2100 = 4200π рад

ε = 24 рад/с 2 4200 – 24 _* 105 2 / 2_/105 = 1220 рад/сек

ω₀ - ? ω - ? ω = ω₀ + ε _* t = 1220 + 24 _* 105 = 3740 рад/сек

Подставив в выражение нормального ускорения а_п = v 2 / r зна­чение скорости v = ωr, получим

a_n = v 2 /r = (ωr) 2 /r = rω 2

Значение полного ускорения вычисляется как диагональ прямоугольника, построенного на составляющих ускорениях a_t и а_п (рис. б). Подставив значения касательного и нормального ускорений, получим

Направление вектора полного ускорения точки вращающегося тела можно определить по углу а, образованному этим вектором с радиусом

Если точка за равные промежутки времени проходит неравные пути, тоee движение называется неравномерным.

Скорость неравномерного движения есть величина переменная и является функцией времени

Рассмотрим точку М, которая перемещается по заданной траек­тории по некоторому закону s = f (t). За промежуток времени Δt точка М переместится в положение М₁ по дуге ММ₁. Если промежуток времени Δt мал, то дугу можно заменить ее хордой и найти в первом приближении среднюю скорость движе­ния точки

Средняя скорость направлена по хорде от точки М к точке М₁. Если постепенно уменьшать промежуток времени Δt , то уменьшается и пройденный путь Δs, т. е. в пределе при Δt → 0 значение средней скорости приближается к значению скорости в заданный момент t т. е. истинную скорость найдем путем перехода к пределу при Δt →0

v = lim Δs/Δt = ds/dt 6

При Δt → О направление хорды в пределе совпадает с направ­лением касательной к траектории в точке М, т. е. значение ско­рости точки определяется как производная пути по времени, а направление ее совпадает с касательной к траектории в данной точке.

Если известны проекции скорости на оси координат, можно определить ее значение и направление:

Если точка за равные промежутки времени проходит неравные пути, тоee движение называется неравномерным.

Скорость неравномерного движения есть величина переменная и является функцией времени

Часто бывает необходимо определить среднюю ско­рость неравномерного движения за некоторый промежуток времени, т. е. скорость такого воображаемого равномер­ного движения, при котором точка проходит за опреде­ленный промежуток времени такой же путь, как и при неравномерном движении.

Пусть S — путь, проходимый точкой при неравномер­ном движении, и t — время, за которое точка проходит этот путь. Средняя скорость определится по формуле

Рассмотрим точку М, за промежуток времени Δt точка М переместится в положение М₁ по дуге ММ₁. Если промежуток времени Δt мал, то дугу можно заменить ее хордой и найти в первом приближении среднюю скорость движе­ния точки

Средняя скорость направлена по хорде от точки М к точке М₁. Если постепенно уменьшать промежуток времени Δt , то уменьшается и пройденный путь Δs (хорда стремится к дуге), т. е. в пределе при Δt → 0 значение средней скорости приближается к значению истиной скорости в момент t т. е. истинную скорость найдем путем перехода к пределу при Δt →0

v = lim Δs/Δt = ds/dt 6

При Δt → О направление хорды в пределе совпадает с направ­лением касательной к траектории в точке М, т. е. значение ско­рости точки определяется как производная пути по времени, а направление ее совпадает с касательной к траектории в данной точке.

Если известны проекции скорости на оси координат, можно определить ее значение и направление:

Выберем произвольную точку М твер­дого тела ( ), вращающегося вокруг неподвижной оси OZ (рис. 10.5). Движение точки М можно описать радиусом-век­тором , который имеет постоянный мо­дуль для выбранной точки:

Дифференцируя (10.5) по времени, нахо­дим скорость:

где , так как вектор постоянен по величине и направлению как производная вектора постоянного модуля по скалярному аргументу.

(h — расстояние от точки до оси вращения).

Вектор скорости будет направлен по касательной к траекто­рии точки М в соответствии с направлением угловой скорости.

Пример 4. Точка А, лежащая на ободе диска, имеет скорость = 40 см/с. Точка В, принадлежащая диску, имеет скорость = 10 см/с (рис. 10.6). Определить угловую скорость диска и его радиус, если расстояние АВ = 15 см.

Решение. Применим формулу (8)

Ответ. R=20 см, ω=2 рад/с.

Получим векторную формулу Эйлера для скорости любой точ­ки твердого тела, вращающегося вокруг неподвижной оси. Из рис. 10.5 видно, что . Тогда . Это выра­жение является модулем векторного произведения , т.е. . Направление вектора скорости определяется век­торным произведением. Следовательно:

Это выражение называют векторной формулой Эйлера.

Скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости на радиус-вектор этой точки, проведенный из произвольной точки на оси вращения.

Определим ускорение точки М:

Рассмотрим слагаемые, входящие в это выражение. Вектор в соответствии с правилом векторного произведения направлен по касательной к траектории точки М, т. е. как касательное уско­рение точки М, которое во вращатель­ном движении называют вращательным ускорением (рис. 10.7):

Величина вращательного ускорения

Вектор находится в плоскости окружности радиуса КМ = h, направлен от точки М к оси вращения и является нормальным ускорением точки М. При вращательном движении это ускорение называют центростремительным ускорением:

Величина центростремительного ускорения:

Модуль полного ускорения точки, вращающегося твердого тела

Угол между полным ускорением и центростремительным равен:

Выражения (10.8) и (10.15) показывают, что скорости и ускорения точек вращающегося твердого тела пропорциональны расстояни­ям от этих точек до оси вращения, а из формулы (10.16) следует, что угол отклонения полного ускорения от центростремительно­го в каждый момент времени один и тот же для всех точек тела.

Уравнение равномерного вращения тела. Вращение тела с постоянной угловой скоростью называется равномерным. Составим уравнение равномерного вращения тела с угловой скоростью ω, принимая направление этоговращения за положительное направление отсчета угла поворота φ.

Положим, что в начальный момент t_o=0 угол поворотаимеет значение φ₀. Тогда

Проинтегрируем уравнение в пределах, соответствующих начальному моменту t₀ = 0 и произвольному моменту времени t:

Выражение (10.17) является уравнением равномерного вращения тела. Если в начальный момент времени подвижная полуплоскость Q совпадает с неподвижной полуплоскостью Р, т. е. φ₀ = 0, то уравнение равномерного вращения тела (10.17) принимает вид

Из уравнения равномерного вращения тела при

т. е. угловая скорость равномерного вращения тела равна отношению приращения угла поворота за некоторый промежуток времени к этому промежутку времени.

Число оборотов, совершаемых вращающимся телом за единицу вре­мени (обычно за минуту), называется частотой вращения и обозна­чаетсяn. Так как один оборот равен 2π радиан, то зависимость между угловой скоростью ω (рад/с) и частотой вращения n (об/мин) имеет вид

Уравнение равнопеременного вращения тела.Вращение тела, при кото­ром угловое ускорение постоянно,называют равнопеременным враще­нием.При этом, если абсолютнаявеличина угловой скорости увеличи­вается, вращениеназывают равноускоренным, иесли уменьшается - равнозамедленным.

Составим уравнение равнопеременного вращения, полагая, что в начальный момент t₀ = 0 начальная угловая скорость , а начальное значение угла поворота φ₀. Тогда

Проинтегрируем уравнение в пределах, соответствующих началь­ному моменту t₀=0 н произвольному моменту времени t:

Проинтегрируем это уравнение в соответствующих пределах:

Уравнение (10.19) является уравнением равнопеременного вращения тела.

Так как равнопеременное вращение происходит обычно в одном направлении, то где знак плюс соответствует уско­ренному вращению, а знак минус - замедленному. Учитывая это, формулам (18) и (19 можно придать более удобный для решения задач вид:

Из формулы угловой скорости находим , т. е. при равно­переменном вращении абсолютное значение углового ускорения тела равно отношению изменения угловой скорости тела за некоторый промежуток времени к числовой величине этого промежутка.

Пример 5. Вал начинает вращаться равноускоренно из состояния покоя; в первые 20 с он совершает 100 оборотов. Каковы егоугловые скорость и ускорение по истечении 20 с?

Решение. Так как вал начинает вращаться из состояния покое, то ω₀=0. В этом случае при φ₀=0

Из уравнения (1) находим

Подставляяв (3) числовые значения, находим

Передаточные механизмы

Передаточные механизмы предназначены для передачи вращения от одною вала. называемого ведущим, к другому, называемому ведо­мым. Если оси ведущего и ведомого валов параллельны или пересекают­ся, то вращение можно передать с помощью фрикционной или зубчатой передачи (рис. 10.8 – 10.11).

Во фрикционной передаче вращение передается вследствие действия силы сцепления на поверхности соприкасающихся колес, в зубчатой передаче - от зацепления зубьев. Вращательная скорость в точке соприкасания колес относится к точкам обоих колес, т. е. ее модуль определяется как

Таким образом, угловые скорости колес фрикционной или зубчатой передачи обратно пропорциональны радиусам колес.

Отношение угловой скорости ведущего колеса к угловой скорости ведо­мого колеса называется передаточным числам:

Рис. 10.8 Рис. 10.9

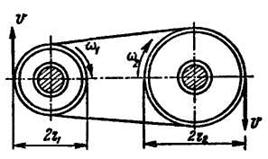
Рис. 10.10 Рис. 10.11

Передаточное число можно вычислить как обратное отношение радиусов колес:

Так как числа зубьев пропорциональны длинам окружностей и, следовательно, радиусам, то передаточное число определяется и по числу зубьев:

При внешнем зацеплении (рис. 10.8) направление вращения ведущего и ведомого колес противоположное, а при внутреннем (рис. 10.9) - одинаковое.

Кроме фрикционной и зубчатой передач существует передача на расстоянии с помощью гибкой связи (ремня, троса, цепи) (рис. 10.11).

Taк как скорости всех точек ремня одинаковы и ремень не скользит по поверхности шкива, то к ременной передаче относятся те же соот­ношения:

Применяются также серии колес с неподвижными осями вращения в виде последовательного ряда с паразитными колесами (рис. 10.12) и последовательного ряда с кратным зацеплением (рис. 10.13), называемые рядовыми соединениями колес.

Рис. 10.12 Рис. 10.13

Определим передаточное число фрикционной передачи в виде рядо­вого соединения с паразитными колесами:

Перемножаем левые и правые части, получаем

Для зубчатых колес

Передаточное число рядового соединения с паразитными колесами равно отношению радиусов (чисел зубьев) ведомого и ведущего колес и не зависит от радиусов (чисел зубьев) паразитных колес.

Определим передаточное число рядового соединения с кратным зацеплением.

Частное передаточное число для колес 1-2

Частное передаточное число для колес 3-4

Так как колеса 2—3 соединены жестко, т. е. то общее передаточное число равно произведению передаточных чисел:

Для зубчатых колес

Таким образом, общее передаточное число рядового соединения колес с кратным зацеплением равно произведению чисел зубьев ведомых колес, деленному на произведение чисел зубьев ведущих колес.

В рассмотренных выше передачах при равномерном вращении ведущего вала ведомый вал вращается тоже равномерно.

Для получения переменной угловой скорости ведомого вала приме­няются передачи, в которых расстояние от точки соприкасания колес до оси одного из валов или обоих валов изменяется.

Рис. 10.14 Рис. 10.15

Во фрикционной передаче, изображенной на рис. 10.14, колесо 1 пере­мещается вдоль его оси и отношение угловых скоростей зависит от переменного расстояния х:

На рис.10.15 изображены эллиптические колеса, оси вращения которых находятся в фокусах эллипсов. Отношение угловых скоростей зависит от переменных расстояний

Пример 1. Вал начинает вращаться равноускоренно из состояния покоя. В первые 20 с он совершает 100 оборотов. Каковы егоугловые скорость и ускорение по истечении 20 с?

Решение. Так как вал начинает вращаться из состояния покое, то ω₀=0. В этом случае уравнения при имеютвид

, (1)

Из уравнения (1) находим

Пример 2. Лебедка (рис. 2.2.1), поднимающая груз по наклонной плоскости, состоит из двух валов 1 л 2 с шестернями (зубчатыми колесами), числа зубьев которых равны соот­ветственно z₁ = 12 и z₂= 48. К валу 2 прикреплен барабан радиусом r= 0,3 м, на который наматывается грузовой трос. Вал 1 вращается равноускоренно с угловым ускоре­нием ε₁ = 8 с –2 . Определить скорость, ускорение и переме­щение груза, а также ускорение точки В барабана в мо­мент времени t = 1 с. В начальный момент времени систе­ма находилась в покое.

Решение. Найдем угловую скорость ω₁ ведущего вала 1 из условия, что оно вращается с угловым ускорени­ем ε₁ = const, учитывая, что . Интегрируя послед­нее уравнение по времени, получаем .

Постоянную интегрирования получаем из начального условия: при t= 0 ω₁ = 0 (система находилась в покое), следовательно C₁ = 0.

Итак, угловая скорость вала 1 определяется уравнени­ем .

При t = 1 с получаем .

Шестерни 1 и 2 взаимодействуют без проскальзыва­ния. Поэтому скорости точек их касания (точка А) будут одинаковы: .

Отсюда находим угловую скорость ω₂ вала 2, учитывая, что :

Угловое ускорение вала 2 равно .

Поскольку трос нерастяжим и относительно барабана не проскальзывает, то скорость груза v будет равна скоро­сти любой из точек на ободе барабана, в частности, скоро­сти точки В: v = v_B = ω₂r = 0,6t=|_{t=1 c} =0,6 м/с.

Ускорение точки В равно векторной сумме касатель­ного (вращательного) и нормального (центростремитель­ного) ускорений: .

Направление вращательного ускорения определяется направлением углового ускорения ε₂, а его модуль равен м/с 2 . Центростремительное ускорение на­правлено к оси вращения вала 2 и равно по модулю м/с 2 .

Модуль ускорения точки В

м/с 2 .

Ускорение груза можно найти, взяв производную по времени от его скорости, так как это касательное ускоре­ние: м/с 2 .

Перемещение груза определяется интегрированием модуля скорости по времени:

Ответ: v = 0,6 м/с; а = 0,6 м/с 2 ; s = 0,3 м; а_B = = 1,34 м/с 2 .

Пример 3. Маховик радиусом R = 0,5 м вращается так, что его угловая скорость меняется в соответствии с уравнением . Для момента времени t = 0,5 с после нача­ла движения определить скорость и ускорение точки на ободе маховика. Установить, за какое время маховик сде­лает 100 полных оборотов.

Решение. Для момента времени t = 0,5 с получаем ω = 0,680 с –1 , и скорость точки на ободе маховика равна v = ωR = 0,340 м/с.

Угловое ускорение маховика

Ускорение точки на ободе маховика равно сумме двух составляющих ускорений: , где и — каса­тельное (вращательное) и нормальное (центростремитель­ное) ускорения точки.

Учитывая, что вращательное ускорение равно по мо­дулю , найдем =0,680 м/с 2 ; центростремительное ускорение . Модуль полного ускорения точки

Направления скорости и ускорений по­казаны на рис. 2.2.2.

Поскольку значения величин угловой скорости и углового ускорения имеют одинаковые знаки, вращение тела уско­ренное. Соответственно, совпадают по направлению угловая скорость и угловое ускорение тела, а также скорость точки и вращательное ускорение.

Поворот маховика на 100 полных оборотов соответ­ствует углу его поворота φ = 200π рад. Выражение для угла поворота найдем из уравнения .

Итак, , откуда находим t = 2,19 с.

Пример 4.Вращение маховикав периодпуска машины определяется уравнением где t–в с, φ - в рад. Определить модуль и направление ускорения точки, отстоящей от оси вращения на расстоянии 50 см, в тот момент, когда ее ско­рость равна 8 м/с.

Решение. По уравнению вращения маховика находим его угловые скорость и ускорение согласно формулам:

Пользуясь формулой, находим момент времени t₁, когда скорость точки М равна 8 м/с:

По этому значению из (1) находимt₁:

По уравнению (2) вычисляем ε, а затем по формулам модуливращательного, центростремительногои полного ускорений точки М в этот момент времена:

Как видно, модуль полного ускорения точки весьма мало отличается от модуля центростремительного ускорения точки (рис. 2.2.3).

Направление ускоренияточки определяетсяуглом β, образованным уско­рениеми радиусом СМ:

Пример 5. Груз А, подвешенный к нити АВ, намотанной на барабан, опу­скается равноускоренно из состояния покоя, приводя во вращение барабан. За первые 3 с барабан совершает 9 оборотов. Определить в конце 5-й секунды скорость и ускорение точки обода барабана, а также груза А, если диаметр барабана D = 30 см (рис. 2.2.4, а).

Решение. Барабан вращается равноускоренно согласно уравнению:

Формула угловой скорости имеет вид:

Для того чтобы начальное значение угла поворота было равно нулю, следует неподвижную полуплоскость поместить в начальном положении под­вижной полуплоскости, вращающейся с барабаном. Выполним это и получим .

При вращении из состояния покоя начальная угловая скорость барабана равна нулю . При этих условиях

Так как при t = 3 с рад, то из уравнения (1) определим угловое ускорение :

Из уравнения (2) найдем угловую скорость барабана в конце 5-й секунды:

Определим в точке В обода барабана (рис. 2.2.4, б) модули вращательной скорости, вращательного и центростремительного ускорений в этот же момент времени по формулам:

(модуль вращательного ускорения точки тела при равнопеременном вращении одинаков для всех моментов времени);

Модуль полного ускорения точки обода барабана определяется по формуле:

Вследствие незначительной величины модуля вращательного ускорения по сравнению с модулем центростремительного ускорения полное ускорение прибли­женно равно центростремительному.

Ускорение груза (рис. 2.2.4, б) равно вращательному ускорению точки обода:

Пример 6. Центробежный регулятор вращается с постоянной угловой скоростью ω вокруг вертикальной оси. Угол АСВ равен 60 о , а ускорение шаров А и В равно по величине 100g, где g=980 см/с 2 . Стержни АС, ВС, АD и BD одинаковой длины l=10 см. Сколько оборотов в минуту делает регулятор (рис. 2.2.5)?

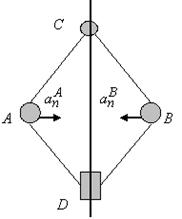
Решение. Для того чтобы найти величину угловой скорости регулятора, напишем зависимость ускорения шара от параметров регулятора. Так как регулятор вращается с постоянной скоростью, то ускорение шара будет центростремительным ускорением, модуль которого определяется формулой

где r – кратчайшее расстояние шара до оси вращения.

С другой стороны, согласно условию, . Приравнивая эти два выражения нормального ускорения шара, находим:

Читайте также:

  
• Электромагнитное воздействие на пласт реферат
  
• Реферат сенсорное воспитание в истории педагогики
  
• Интеллигенция и революция реферат
  
• Право проживания в чужом жилом помещении реферат
  
• Инвестиционная привлекательность финансовых инструментов реферат