Реферат замена переменных в тройном интеграле
Обновлено: 07.07.2024
1. Тройной интеграл в цилиндрических координатах. В случае так называемых цилиндрических координат положение точки Р в пространстве определяется тремя числами , где — полярные координаты проекции точки Р на плоскость Оху — аппликата точки Р, т. е. расстояние точки до плоскости взятое со знаком плюс, если точка лежит выше плоскости и со знаком минус — если ниже (рис. 336).
Пределы интегрирования определяются формой области V.
Если дан тройной интеграл от функции в прямоугольных координатах, то его легко преобразовать в тройной интеграл в цилиндрических координатах. В самом деле, заметив, что
Пример Определить массу М полушара радиуса R с центром в начале координат, если плотность F его вещества в каждой точке пропорциональна расстоянию этой точки от основания, т. е.
Решение. Уравнение верхней части полусферы
в цилиндрических координатах имеет вид
2. Тройной интеграл в сферических координатах, В сферических координатах положение точки Р в пространстве определяется тремя числами где — расстояние точки от начала координат, так называемый радиус вектор точки, угол между радиус-вектором и осью между проекцией радиус-вектора на плоскость Оху и осью Ох, отсчитываемый от этой оси в положительном направлении (т. е. против часовой стрелки) (рис. 338). Для любой точки пространства имеем
Разобьем данную область V на элементарные частй координатными поверхностями поверхности с вершинами в начале координат), (полуплоскости, проходящие через ось точностью до бесконечно малых высшего порядка элементарный объем Ди можно считать параллелепипедом с ребрами длины Тогда элементарный объем равен (рис. 339)
Тройной интеграл от функции по области V имеет вид
Границы интегрирования определяются формой области V.
Из рис. 338 легко устанавливаются выражения декартовых
координат через сферические:
Поэтому формула преобразования тройного интеграла от декартовых координат к сферическим имеет вид
3. Общая замена переменных в тройном интеграле. Переходы от декартовых координат к цилиндрическим и сферическим в тройном интеграле — это частные случаи общего преобразования координат в пространстве.
взаимно однозначно отображают область V в декартовых координатах х, на область V в криволинейных координатах . Пусть элемент объема области V переходит в элемент области V и пусть
Аналогично тому, как это имело место в двойном интеграле, I называется якобианом; подобно тому как это делалось для
двойных интегралов, можно доказать, что якобиан численно равен определителю третьего порядка:
Пусть преобразование,, отображает область Е взаимно однозначно на область G в пространства с переменными u, v, w, причём обратное отображение области G на область Е осуществляеется преобразованием, ,. Функции, , — непрерывные вместе с частными производными, а якобиан на области G неравен нулю: Замечание 1. Рассмотренное отображение называется регулярным. Можно доказать, что при регулярном… Читать ещё >
- интегрирование функций нескольких переменных
Замена переменной в тройном интеграле ( реферат , курсовая , диплом , контрольная )
Пусть функция есть непрерывная на ограниченым области Е.
Пусть преобразование, , отображает область Е взаимно однозначно на область G в пространства с переменными u, v, w, причём обратное отображение области G на область Е осуществляеется преобразованием, ,. Функции, , — непрерывные вместе с частными производными, а якобиан на области G неравен нулю:

Рассуждая аналогично тому, как и при выводе формулы замены переменных в двойном интеграле, получаем формулу замены переменных в тройном интеграле:



Замечание 1. Рассмотренное отображение называется регулярным. Можно доказать, что при регулярном отображении образом гладкой поверхности является гладкая поверхность; образом границы — граница; образом области является область, а также имеет место следующая теорема.
Теорема 1. Если функция f непрерывная на теле ЕOxyz и = — регулярное отображение тела Ouvw на тело Е, где тела Е и G — замкнутые кубируемые, то имеет место равенство (1) § 5, которое называют формулой замены переменных в тройном интеграле.
Тройка чисел однозначно характеризует положение точки в пространстве 0xyz и называется кривалинейными координатами этой точки. Поверхности в пространстве 0xyz, определяемые равенствами v=const, u=const, w=const, называются координатными поверхностями. Через каждую точку области Е проходит по одной поверхности из каждого семейства координатных поверхностей.
Рассмотрим два частных случая кривалинейных координат в пространстве R 3 , которые широко используются при вычислении тройных интегралов методом замены переменных.
Цилиндрические координаты Пусть точека М в прямоугольной декартовай системе координат 0xyz имеет координаты. Задавая проекцию точки М на плоскость при помощью полярных координат r, положение точки М можно определить с помощью трёх чисел, которые называт цилиндрическими координатами точки М. Если полярная ось совпадает с положительным направлением оси 0х, то формулы:
Координатной поверхностью в цилиндрической системе координат являются: цилиндрические поверхности r=const, полуплоскости =const, которая проходит через ось 0z, и плоскость z=const, параллельная х0у.
Пусть система координат отображается на систему координат 0xyz по формулам (2), т. е. , тогда якобиан этогоотображения:

Замечание 2. Если область Е в пространстве 0xyz можно задать в цилиндрических координатах неравенствами, , то тройной интеграл сводится к повторному интегралу.



Пусть точка М (x, y, z) в прямоугольной системе координат 0xyz знаходится на расстоянии от начала координат О. Обозначим через угол между положительным направлением оси 0z и вектором. Пусть есть полярный угол проекции точки М на плоскость х0у. Тогда положение точки М можно задать с помощью трёх чисел, которые называют сферическими координатами точки М. Сферические координаты связаны с декартовыми следующими формулами:
Координатными поверхностями в сферических координатах являются: сфера, полуплоскость, которая проходит через ось 0z, и коническая поверхность с осью 0z.
Найдём якобиан преобразования (5):

На основании равенства (1) § 3 выводим формулу замены переменных в сферических координатах:

Замечание 3. Если область Е в пространстве 0xyz можно задать в сферических координатах неравенствами, то тройной интеграл (5) сводится к повторному интегралу.
Пусть в пространстве $\mathbf < \textit < Ouvw >> $ задана область $\mathbf < \textit < G >> $, и пусть отображение $F(M)=M^\ast $ преобразует эту область в область $\mathbf < \textit < V >> $ пространства $\mathbf < \textit < Oxyz >> . $ Будем считать, что отображение $\mathbf < \textit < F >> $ задаётся функциями $F:\left[ < \begin < l >x=x(u,v,w) \\ y=y(u,v,w) \\ z=z(u,v,w) \\ \end >\right.$.
Доказательство этой теоремы аналогично доказательству теоремы о замене переменных в двойном интеграле.
Рассмотрим наиболее часто употребляемые криволинейные системы координат в пространстве - цилиндрические и сферические.
Тройной интеграл в цилиндрических координатах
В этой координатной системе положение точки в пространстве характеризуется тремя числами: $\mathbf < \textit < r >> $, $\varphi $ и $\mathbf < \textit < z >> $, где $\mathbf < \textit < r >> $ и $\varphi $ - полярные координаты проекции $\mathbf < \textit < M >> ^ < 1 >$
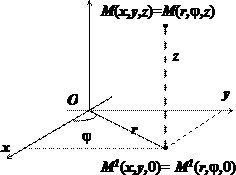
точки $\mathbf < \textit < М >> $ на плоскость$\mathbf < \textit < Оху >> $, $\mathbf < \textit < z >> $ - аппликата точки $\mathbf < \textit < M >> $. Формулы перехода от цилиндрических координат к декартовым: $ \begin < l >x=r\cos \varphi , \\ y=r\sin \varphi , \\ z=z. \\ \end $
Тройной интеграл в сферических координатах
В этих координатах положение точки $\mathbf < \textit < M >> $ в пространстве характеризуется тремя числами: $\mathbf < \textit < r >> $, $\varphi $ и $\theta $, где $\mathbf < \textit < r >> $ - длина радиуса-вектора точки $\mathbf < \textit < M >> $, $\varphi $ - полярный угол проекции $\mathbf < \textit < M >> ^ < 1 >$точки $\mathbf < \textit < М >> $ на плоскость$\mathbf < \textit < Оху >> $, $\theta $ - угол между радиусом-вектором точки $\mathbf < \textit < M >> $ и осью $\mathbf < \textit < Oz >> $. Формулы перехода от сферических координат к декартовым: $ \begin < l >x=r\sin \theta \cos \varphi , \\ y=r\sin \theta \sin \varphi , \\ z=r\cos \theta . \\ \end $
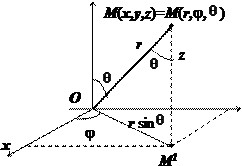
Вычислим якобиан этого преобразования:
$=\left| < \begin < l >\;\;\sin \theta \cos \varphi \quad \;\;\;\;\;\sin \theta \sin \varphi \;\;\quad \cos \theta \\ -r\sin \theta \sin \varphi \quad \;\;r\sin \theta \cos \varphi \;\;\;\;\;\quad 0 \\ \;\;r\cos \theta \cos \varphi \quad r\cos \theta \sin \varphi \;\;-r\sin \theta \\ \end >\right|=r^2\sin \theta \left| < \begin < l >\sin \theta \cos \varphi \;\;\;\;\sin \theta \sin \varphi \;\;\quad \cos \theta \\ \;-\sin \varphi \quad \;\;\;\;\cos \varphi \;\;\;\;\;\;\;\;\;\quad 0 \\ \cos \theta \cos \varphi \quad \cos \theta \sin \varphi \;\;-\sin \theta \\ \end >\right|= \\ =r^2\sin \theta \left[ < \cos \theta (-\cos \theta \sin ^2\varphi -\cos \theta \cos ^2\varphi )-\sin \theta (\sin \theta \cos ^2\varphi +\sin \theta \sin ^2\varphi ) >\right]=-r^2\sin \theta ,$ следовательно, $\iiint\limits_V < f(x,y,z)dxdydz >=\iiint\limits_ < V_ < r,\varphi ,\theta >> < f(r\sin \theta \cos \varphi ,r\sin \theta \sin \varphi ,r\cos \theta )\cdot r^2\sin \theta \cdot drd\varphi d\theta >$.
Далее:
Теорема о заведомо полныx системаx
Нахождение потенциала
Теорема об алгоритме распознавания полноты
Примеры применения цилиндрических и сферических координат
Логические следствия
Вычисление криволинейного интеграла второго рода. Примеры.
Вычисление объёмов
Теорема об аналоге СДНФ в Pk
Вычисление криволинейного интеграла первого рода. Плоский случай
Лемма о построении множества $[F]_$
Формула Грина
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Если ограниченная замкнутая областьПространстваВзаимно однозначно отображается на областьПространстваС помощью непрерывно дифференцируемых функций

(20.4)

В областиНе обращается в нуль, т. е.То замена переменных в тройном
Интеграле осуществляется по формуле

(20.6)

В частности, при переходе от декартовых координатК цилиндрическим
Координатам(см. п. 1.14), связанным сФормулами

При переходе от декартовых координатК сферическимСвязан

Ным сСоотношениями

(20.9)

Якобиан преобразованияИ формула (20.6) принимает вид

(20.10)

Пример 20.4. Вычислить тройной интеграл,
Где областьЕсть шар
Перейдем к сферическим координатам по формулам (20.9). В области, являющейся образом областиПри преобразовании (20.9) переменныеМеняются. в следующих пределах:ОтДоОтДо,ОтДо Так как подынтегральная функция

, а якобиан преобразования

(20.9) равен, то по формуле (20.10) получим

Пример 20.5. Вычислить тройной интегралГде-

Область, ограниченная верхней частью конусаИ плос

Костью
Введем цилиндрическиекоординаты по формулам (20.7). Уравнение конуса принимает вид, или
Новые переменные в областиИзменяются в следующих пределах:ОтДо ОтДоОтДо
По формуле (20.8) получаем


Пример 20.6. Вычислить, где
ОбластьОграничена эллипсоидом
Введем так называемые обобщенные сферические координаты по формулам

(20.11)
Якобиан преобразования (20.11), определяемый формулой


РавенПодынтегральная функция по формулам (20.11) преобразуется к

Виду, а уравнение эллипсоида запишется так:
, или
В областиПеременныеИзменяются в следующих пределах:ОтДо
ОтДоОтДо По формуле (20.6) получаем


С помощью подстановкиНаходим первый интеграл:


Далее,Поэтому


Пример 20.7. Вычислить тройной интеграл
Где областьОграничена цилиндромИ плоскостями
Перейдем к цилиндрическим координатам по формулам * = pcos
Тогда уравнение цилиндраПримет вид
А подынтегральная функция запишется так:

При таком переходе к цилиндрическим координатам замена переменных в тройном интеграле будет осуществляться по формуле





Грал где- шар

Данный интеграл является несобственным, так как подынтегральная функция не ограничена в рассматриваемой области (она обращается в бесконечность на границе области, т. е. на сфере _).
Выражаем этот интеграл в сферических координатах. Так как в данном случае

То по формуле (20.10) получаем
Изложенная теория двойного интеграла без каких-либо осложнений и новых идей переносится на случай тройного интеграла. Остановимся лишь на формуле повторного интегрирования для тройного интеграла.
Пусть – плоская область, ограниченная кусочно-гладкой кривой и–цилиндрический брус, ограниченный снизу - поверхностью,сверху -поверхностью,, с боку - цилиндрической поверхностью с образующей, параллельной осии направляющей-границей области.
Если функция непрерывна в, то справедливо равенство

.
§ 8. Замена переменных в двойном и тройном интегралах.
Формула замены переменных является одним из важнейших средств вычисления кратных интегралов.
1) Замена переменных в двойном интеграле.
Предположим, что функция интегрируема в области. Предположим далее, что от переменныхмы переходим к переменным, то есть совершаем преобразование

; (*)
Обозначим через ту область в, которая при преобразовании (*) переводится в.
Если преобразование (*) переводит область ви является взаимно однозначным и если функции (*) имеют внепрерывные частные производные первого порядка по всем переменным и отличный от нуля якобиан, то для каждой интегрируемой вфункциисправедлива формула замены переменных:

.
Замечание 1. В условиях теоремы можно допустить обращение в нуль якобиана на некотором принадлежащем множестве точек, имеющем площадь нуль, а также допустить неоднозначность отображения на таком же множестве.
Наиболее часто при вычислении двойных интегралов переходят от декартовых к полярным координатам.
, ,,.

.
2) Замена переменных в тройном интеграле.
В случае тройных интегралов справедлива аналогичная теорема. Отметим две наиболе важных замены переменных.
1. Сферические координаты.
, ,,

.
2. Цилиндрические координаты.
, ,,

.
§ 9. Криволинейные интегралы.
, .


Называют длиной траектории Г, или длиной годографа вектор-функции . С этим понятием связано понятие криволинейного интеграла 1-го типа.
Определение. Пусть вектор-функция имеет на отрезкенепрерывную производную. Пусть функцияопределена на множестве Г. Тогда интеграл

,
если он существует, называется интегралом от функции по длине дуги траектории Г и обозначается. Этот интеграл называют также криволинейным интегралом 1-го типа.
Криволинейному интегралу 1-го типа можно дать физическое истолкование. Прежде всего, напомним, что если материальная точка единичной массы перемещается из точки в точкупод действием постоянной силы . Если действующая сила не является постоянной, а зависит от положения точки, то производимую работу естественно считать по формуле

.
В обоих этих примерах мы считали, что действующая сила направлена в сторону движения точки. Пусть теперь материальная точка единичной массы перемещается вдоль траектории Г, заданной уравнением ,, под действием силы, зависящей от положения точки и направленной вдоль Г, то есть в направлении вектора. Тогда эта материальная точка производит работу, которую можно вычислить по формуле

.

Таким образом, криволинейный интеграл 1-го типа можно истолковать как работу, производимую при перемещении точки вдоль траектории Г под действием силы , направленной по касательной к Г.
Ту же задачу вычисления работы, которую производит перемещающаяся точка, можно решать с векторной точки зрения. Пусть материальная точка единичной массы под действием постоянного вектора силы перемещается вдоль вектора, то есть перемещается, например, из начала координат в точку с координатами. Как известно, при этом будет произведена работа. Пусть теперь вектор силы зависит от положения точки на векторе. Обозначим координаты векторадля удобства через. Тогда можно считать, что. Работу, которую производит перемещающаяся точка, естественно вычислять по формуле

Здесь через обозначен векторПусть, наконец, материальная точка единичной массы перемещается вдоль траектории Г, заданной уравнением,, под действием силы, зависящей от положения точки. Тогда эта материальная точка производит работу, которую можно вычислить по формуле

С этим понятием работы связано понятие криволинейного интеграла 2-го типа.
Определение. Пусть вектор-функция имеет на отрезкенепрерывную производную и пусть Г есть годограф вектор-функцииили, другими словами, траектория, заданная уравнением,. Пусть вектор-функцияопределена на множестве Г.
Тогда интеграл


Если он существует, называется криволинейным интегралом 2-го типа от вектор-функции по траектории Г и обозначается
, или .
Как видим физическое истолкование криволинейных интегралов 1-го и 2-го типов отличается лишь тем, что в первом случае работа вычисляется при условии, что действующая сила направлена по касательной к траектории Г, а во втором случае вектор силы имеет произвольное направление. Разумеется, нетрудно свести один случай к другому. В самом деле, если вектор силы, а траектория Г имеет касательную, составляющую с осями координат углыи, то в направлении этой касательной будет действовать сила величиной. Это дает повод установить связь между криволинейными интегралами 1-го и 2-го типа.
Теорема. Пусть вектор-функция имеет на отрезкенепрерывную производнуюи пусть Г есть траектория, заданная уравнением,. Пусть вектор-функциянепрерывна на можестве Г. Тогда имеет место равенство

,
где и- это углы, образуемые касательной к траектории Г с координатными осямии, причем направление касательной соответствует возрастанию дуг траектории от точкидо точки.
Доказательство. Прежде всего заметим, что в силу непрерывности вектор-функции оба криволинейных интеграла, указанных в теореме существуют. Далее, еслии- это углы, указанные в теореме, то они вычисляются из соотношений
, ,
где - единичные векторы, соответствующие координатным осями. Отсюда следует, что
Читайте также:

