Реферат по теме параллельные прямые и углы образованные ими

Обновлено: 07.07.2024

Параллельные прямые — две прямые, которые лежат в одной плоскости и не пересекаются, а || b.

Аксиома параллельности:
Через точку, не лежащую на данной прямой, на плоскости можно провести только одну прямую , параллельную данной прямой.

Выделенная синим цветом часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского. В геометрии Лобачевского через точку, лежащую за прямой, проходит множество прямых, которые не пересекают данную прямую.

Иногда Аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.

Примечание. В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Свойства и признаки параллельных прямых

Свойства и признаки параллельных прямых:

Две прямые, параллельные третьей, параллельны.
Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Если две параллельные прямые пересечены секущей, то:
– сумма внутренних односторонних углов равна 180°,
– накрест лежащие углы равны,
– соответственные углы равны,

Теорема Фалеса:
Если на одной из двух прямых отложено несколько равных отрезков и через их концы проведены параллельные прямые, не пересекающие другую прямую, то и на ней отложатся равные отрезки.

Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Параллельность Прямых на Плоскости

Качанова И.А 11.02.2014г

1.Параллельность прямых на плоскости

Учение о параллельности прямых в курсе планиметрии можно разделить на следующие части:

- определение параллельных прямых;

- существование параллельных прямых;

- построение параллельных прямых;

- свойства параллельных прямых;

- признаки параллельности прямых;

- применение изученной теории к решению задач.

Резко очерченных границ между выделенными частями не может быть, последний раздел, безусловно, присутствует во всех предыдущих.

Формулировки определений параллельных прямых в учебных пособиях, так же как и подходы к их изучению, различны.

В учебном пособии по геометрии А.В. Погорелова и в пробном учебнике Л.С. Атанасяна рассматриваются только два случая взаимного расположения прямых на плоскости: прямые пересекаются (имеют только одну общую точку) и прямые не пересекаются (совсем не имеют общих точек). Поэтому и определения параллельных прямых в этих пособиях даются соответствующим образом:

Опр. Две прямые называются параллельными, если они не пересекаются.

Опр. Прямые на плоскости не имеющие общих точек называются параллельными.

Эти определения параллельных прямых на плоскости эквивалентны друг другу.

В учебном пособии по геометрии под редакцией А.Н. Колмогорова рассматриваются три случая взаимного расположения двух прямых на плоскости:

- прямые имеют только одну общую точку;

- прямые совпадают (все точки общие);

- прямые совсем не имеют общих точек.

Два последних случая входят в определение параллельных прямых в этом учебнике.

В процессе работы над определением параллельных прямых следует особо выделить, что они лежат в одной плоскости, и требовать этого постоянно от учащихся; такая работа поможет избежать нежелательных ошибок в дальнейшем при изучении соответствующих вопросов в курсе стереометрии. В качестве контр примера полезно наглядно показать прямые пространства, которые не лежат в одной плоскости, не имеют общих точек и не являются параллельными (скрещивающиеся прямые).

Две прямые называются параллельными, если они:

2) не пересекаются.

1) лежат в одной плоскости;

2) не имеют общих точек.

1) лежат в одной

2) не имеют общих точек.

Вопрос о существовании параллельных прямых также решается неодинаково в имеющихся учебных пособиях. К примеру в учебнике А.В. Погорелова "Геометрия7-11" этот вопрос рассматривается следующим образом: рассматривается аксиома параллельных, а затем доказывается теорема, показывающая существование таких прямых

Аксиома. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Существование параллельных прямых обосновывается в школе двумя путями, а именно на основе центральной симметрии или на основе свойств углов, образованных при пересечении двух прямых третьей.

Доказательство теоремы везде ведется методом от противного. Однако предложения, на основе которых делается окончательный вывод, различны: в одних случаях это свойство двух различных прямых не иметь двух и более различных общих точек; в других случаях это свойство внешнего угла треугольника не быть меньшим или равным внутреннему углу этого треугольника, не смежному с ним. Доказательство теоремы опирается на представление учащихся о неограниченности и бесконечности прямой, что сопряжено с большими трудностями, связанными с потерей наглядности чертежа, противоречием правильным интуитивным представлениям учащихся.

Вследствие этого чертежу желательно уделить особое внимание при доказательстве теоремы, при изображении точки пересечения прямых желательно не делать изломов.

Теоремы - признаки параллельности прямых требуют тщательной методической разработки, их доказательство надо сопровождать соответствующими записями. В качестве примера рассмотрю соответствующую теорему по учебному пособию под редакцией А.Н. Колмогорова:

Теорема. "Если две прямые симметричны относительно некоторого центра, то они параллельны".

Запись этой теоремы с ее доказательством может

выглядеть следующим образом:

Признак параллельности прямых.

Дано: прямые а и b, b=Z0(a).

Доказательство(метод от противного)

1. Пусть а и b различны и

непараллельные, т.е. а и b имеют

2. С отлична от O, так как b и

3. С и Z0(C)=C1 различны, так как С не совпадает с О.

4. C1 принадлежит прямым а и b, так как С принадлежит этим прямым.

5. Прямые а и b имеют две различные общие точки С и C1, что

6. Предположение, что а и b непараллельные, неверно. Значит, а и b параллельны.

7. Если а и b центрально-симметричны и совпадают то они параллельны, по определению.

Раздел об углах, образующихся

при пересечении двух прямых третьей.

Рисунок к введению этих понятий

не должен отражать частных случаев: две

прямые не должны изображаться параллельными,

а секущая не должна быть к ним перпендикулярной (рис-2).

Прямые а и b разбивают плоскость на три части: две внешние и одну внутреннюю.

Из восьми углов, образующихся при пересечении прямых а и b прямой с, некоторые лежат по одну сторону от прямой с, другие по разные стороны от прямой с. Некоторые из углов, расположенных по разные стороны от прямой с, получили название накрест лежащих;

некоторые углы, расположенные по одну сторону от прямой с, получили название или односторонних или соответственных. В зависимости от того, в каких из названных частей расположены углы, различают внутренние и внешние накрест лежащие углы (3 и 6, 4 и 5, 1 и 8, 2 и 7), внутренние или внешние односторонние углы (4 и 6, 3 и 5, 1 и 7, 2 и 8), соответственные углы (2 и 6, 1 и 5, 4 и 8, 3 и 7).

Большую роль в изучении параллельных прямых играет аксиома параллельных прямых.

В имеющейся учебной литературе приведены различные формулировки аксиомы параллельных:

1.Аксиома. Через данную точку проходит не более одной прямой, параллельной данной прямой.

2.Аксиома. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

3.Аксиома. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной .

Требование, чтобы точка не лежала на данной прямой, связано с тем, что в этих учебных пособиях совпадающие прямые не считаются параллельными и вообще не рассматриваются. Надо отметить, что в третьем случае аксиома является более сильной, чем в первом и во втором случае. Утверждение, что через точку проходит только одна прямая, параллельная данной прямой, в первом случае можно доказать:

"Через данную точку можно провести не более одной прямой, параллельной данной" - на основе аксиомы;

"Через данную точку можно провести одну прямую, параллельную данной" - на основе теоремы существования и построения.

Следовательно, через данную точку проходит только одна прямая, параллельная данной прямой. Эти рассуждения приводятся не во всех учебных пособиях для средней школы.

В процессе изучения параллельности прямых весьма важно обращать внимание на раскрытие роли аксиомы параллельности при построении темы. При доказательстве соответствующих теорем, где явно используется аксиома параллельных, этот пункт доказательства

желательно особо выделить.

Теорема. Две прямые, параллельные третьей, параллельны. .

Дано: а, b и с - прямые, а││с и b││с.

Доказательство (рис. 3).

1. Пусть прямые а и b не параллельны, т.е. а и b пересекаются в некоторой точке С.

2. Через точку С проходят две прямые а и b, параллельные прямой С, что противоречит аксиоме параллельных.

3. Предположение, что прямые а и b не параллельны, неверно. Значит, а││b. Ч.т.д.

При изложении курса геометрии большое значение имеют как

теоремы - признаки параллельности, так и теоремы, им обратные.

Достаточно доказать один из признаков параллельности прямых, основанных на углах, образованных при пересечении двух прямых третьей, а остальные признаки параллельности свести к уже доказанному.

Особый интерес представляет методика работы над теоремами - признаками параллельности прямых в соответствии с учебным пособием по геометрии А.В. Погорелова и пробным учебником по геометрии Л.С. Атанасяна (Рис-4):

Дано: с - секущая для прямых а и b;

угол 1 и угол 2 - внутренние накрест лежащие; 1=2.

Доказательство: (метод от противного).(Таблица-2)

Доказательства признака параллельности прямых

По учебному пособию

По пробному учебнику

т.е. пересекаются в точке с.

Точку Е на прямой b.

3. ∆ВАD=∆АВС по первому признаку

4. ABD=BAC, так как

5. ABE=BAC, так как 1=2.

6. ABD=ABE как равные одному и тому же ВАС.

7. Лучи BD и BE совпадают, так как ABD=ABE (аксиома откладывания углов)

8. D принадлежит прямой b, так как лучи BD и BE совпадают.

9. Прямые а и b имеют две различные общие точки D и С, что невозможно.

10. Предположение, что а и b

пересекаются, неверно. Значит, а││b.

1. Пусть а и b не параллельны,

т.е. имеют общую точку С.

2. 2 внутренний в ∆АВС, а

1 внешний в ∆АВС.

1>2 по теореме о внешнем

Это противоречит условию

4. Предположение, что а и b

не параллельны, неверно.

Перед доказательством признаков параллельности прямых необходима специальная работа по организации повторения тех вопросов, которые составляют основу доказательства, а именно: Организация повторения вопросов которые составляют основу доказательства признака параллельных прямых.(Таблица-3)

Организация повторения вопросов которые составляют основу доказательства признака параллельных прямых

По учебному пособию

а) признаки равенства

треугольников и определение

б)аксиома откладывания углов;

в) углы, образуемые при пересечении двух прямых третьей;

г) свойство смежных углов.

а) углы, образуемые при пересечении двух прямых третьей;

б) нахождение на рисунке внутренних углов треугольника и внешних его углов;

в) нахождение на рисунке внутренних углов треугольника, не смежных с данным внешним его углом;

г) свойства внешнего угла треугольника.

Повторение проводится по рисункам, при этом предполагается их варьирование во избежание частных случаев.

По содержанию задачи по этой теме можно разделить на три группы:

1) Задачи на прямое применение аксиомы параллельности:

"Доказать, что две прямые, параллельные третьей прямой, параллельны";

2) Задачи на применение признаков параллельности прямых:

"Доказать, что биссектрисы соответственных углов, образованных при пересечении двух параллельных прямых третьей прямой, параллельны";

3) Задачи на применение теорем, обратных признакам

параллельности прямых: "Через вершину А треугольника АВС проведена

прямая, параллельная противоположной стороне его. Зная углы треугольника, вычислить углы, образовавшиеся при вершине А".

2. Параллельность прямых в пространстве. Скрещивающиеся прямые

Учение о параллельности прямых в курсе стереометрии можно разделить на следующие части.

- Определение параллельных и скрещивающихся прямых;

- Теорема о параллельных прямых;

- Признак параллельных прямых;

- Применение изученной теории к решению задач.

Так как данная геометрическая линия более подробно мной рассмотрена во второй главе в третьем пункте данной работы, то ограничусь в своем рассуждении в данном пункте, сравнением двух учебников: учебник "Геометрия 7-11" под редакцией А.В. Погорелова и учебником "Геометрия 10-11" под редакцией Л.С. Атанасяна.

Определения параллельных и скрещивающихся прямых в обоих учебниках звучат одинаково и являются ключевыми во всей теме, но вводятся они по разному (Таблица-4 ). В учебнике А.В. Погорелова определение параллельных и скрещивающихся прямых дается сразу в течении первого урока, а в учебнике Л.С. Атанасяна на первом уроке дается определение параллельных прямых и только после того как пройдет изучение признака параллельных прямых дается понятие скрещивающихся прямых в виде небольшой темы.

Определение параллельных и скрещивающихся прямых

"Геометрия 7-11" под редакцией

"Геометрия 10-11" под редакцией

Опр. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Опр. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.

Теорема о параллельных прямых и ее доказательство в обоих

учебниках рассматривается на первом занятии и представляется в

следующем виде (Таблица-5):

Теорема о параллельных прямых и ее доказательство

"Геометрия 7-11" редакцией

"Геометрия 10-11" под редакцией Л.С. Атанасяна

Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну

Через любую точку пространства,

не лежащую на данной прямой,

ходит прямая, параллельная данной и притом только одна

1) Пусть а - данная прямая и А - точка, не лежащая на этой прямой. Проведем через прямую а и точку А плоскость z. Проведем через точку А в плоскости z прямую а1, параллельную а. Докажем, что прямая а1, параллельная а, единственна. Рис-а

2) Допустим, что существует другая прямая а2, проходящая через точку А и параллельная прямой а. Через прямые а и а2 можно провести плоскость z2.

3) Плоскость z2 проходит через прямую а и точку А; следовательно, по теореме (Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну) она совпадает с z

4) Теперь по аксиоме параллельных прямые а1 и а2 совпадают. ч.т.д.

1) Рассмотрим прямую а и точку М, не лежащую на этой прямой. Через прямую а и точку М проходит плоскость, и притом только одна. Обозначим эту плоскость буквой z.

2) Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. должна лежать в плоскости z.

3) Но в плоскости z, как известно из курса планиметрии через точку М проходит прямая, параллельная прямой а, и притом только одна. На рис-б эта прямая обозначена буквой b.

4) Итак, b-единственная прямая, проходящая через точку М параллельно прямой

В учебнике Л.С. Атанасяна разбирается такое понятие, как параллельность трех прямых. И выдается следующие утверждение в виде леммы.

Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Признак параллельных прямых и его доказательство в обоих учебниках рассматривается на втором занятии и представляется в следующем виде (Таблица-6):

Признак параллельных прямых.

Геометрия 7-11" под редакцией А.В. Погорелова

"Геометрия 10-11" под редакцией Л.С. Атанасяна.

Две прямые, параллельные третей прямой, параллельны.

Если две прямые параллельны

третей прямой, то они параллельны.

1)Пусть z - плоскость, в которой

Лежат прямые а и b, а v плоскость, в которой лежат прямые а и с. Плоскости z и v различны.(Рис-в)

2)Отметим на прямой b какую ни будь точку В и и проведем плоскость v1 через прямую с и точку В. Она пересечет плоскость z по прямой b1. Прямая b1 не пересекает плоскость v. 3)Действительно, точка пересечения должна принадлежать прямой а, так как прямая b1 лежит в плоскости z. С другой стороны, она должна лежать и на прямой с, так как прямая b1 лежит в плоскости v1. Но прямые а и с как параллельные не пересекаются. Так как прямая b1 лежит в плоскости z и не пересекает прямую а, то она параллельна а, а значит совпадает с b по аксиоме параллельных.

4)Таким образом, прямая b, совпадя с прямой b1, лежит в одной плоскости с прямой с (в плоскости v1) и не пересекает ее. Значит, прямые b и с параллельны. ч.т.д.

Пусть а││с и b││c. Докажем, что

а││b. Для этого нужно доказать,

что прямые а и b: 1) лежат в

одной плоскости и 2)не пересекаются.

1) Отметим какую-нибудь точку К

на прямой b и обозначим буквой z

плоскость, проходящую через прямую а и точку К (рис-г). Докажем, что прямая b лежит в этой плоскости. Действительно, если допустить, что прямая b пересекает плоскость z, то по лемме о пересечении плоскости параллельными прямыми прямая с также пересекает плоскость z. Но так как с││а, то и прямая а пересекает плоскость z

что невозможно, ибо прямая а лежит в плоскости z.

2) Прямые а и b не пересекаются,

так как в противном случае через

точку их пересечения проходили бы

две прямые (а и b), параллельные

прямой с, что невозможно. ч.т.д.

Не безынтересно в конце данной геометрической линии провести сравнение на плоскости и в пространстве прямых, не имеющих общих точек. (Схема-1) [5]

На плоскости

Прямые не имеют общих точек

Лежат в одной плоскости

Параллельные прямые

Лежат в одной плоскости

Не лежат в одной плоскости

Узнать стоимость написания работы -->

При пересечении двух прямых образуются вертикальные и смежные углы.

Вертикальные углы — равны.

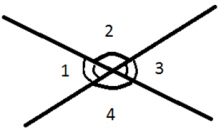
Сумма смежных углов равна 180°.

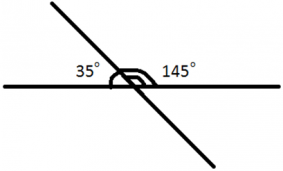
Параллельные прямые

Прямые называются параллельными, если они не пересекаются, сколько бы их не продолжать.

О параллельных прямых:

Если одна из пары параллельных прямых параллельна третьей прямой, то все прямые параллельны между собой.
На плоскости через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.

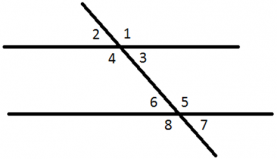
При пересечении двух параллельных прямых секущей образуются следующие углы:

внутренние накрест лежащие (4 и 5, 3 и 6) — попарно равны;
внешние накрест лежащие (1 и 8, 2 и 7) — попарно равны;
соответственные (1 и 5, 2 и 6, 3 и 7, 4 и 8) — попарно равны;
внутренние односторонние (3 и 5, 4 и 6) — сумма таких углов равна 180°;
внешние односторонние (1 и 7, 2 и 8) — сумма таких углов равна 180°.

Часто для использования свойств углов, полученных при пересечении двух параллельных прямых секущей, необходимо применять дополнительные построения.

Пример: Даны углы с попарно параллельными сторонами. Что можно сказать об углах 1 и 2? Что можно сказать об углах 3 и 4?

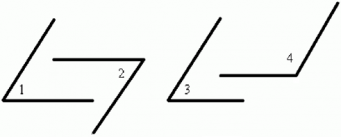
Продолжим стороны углов до пересечения:

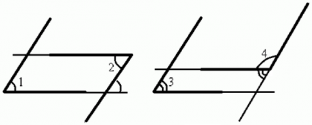
Получаем, что углы 1 и 2 равны, т. к. являются накрест лежащими при параллельных прямых.

Сумма углов 3 и 4 равна 180°, т. к. они являются односторонними при параллельных прямых.

Теорема Фалеса: При пересечении сторон угла параллельными прямыми стороны угла делятся на пропорциональные отрезки (образуются подобные треугольники).

Параллельные прямые — две прямые, которые лежат в одной плоскости и не пересекаются, а || b.

Свойства и признаки параллельных прямых

Свойства и признаки параллельных прямых:

Две прямые, параллельные третьей, параллельны.
Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Если две параллельные прямые пересечены секущей, то:
– сумма внутренних односторонних углов равна 180°,
– накрест лежащие углы равны,
– соответственные углы равны,

Будь умным!

Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.

«>Параллельность Прямых на Плоскости

«>1.Параллельность прямых на плоскости

«>Учение о параллельности прямых в курсе планиметрии можно разделить на следующие части:

«> — определение параллельных прямых;

«> — существование параллельных прямых;

«> — построение параллельных прямых;

«> — свойства параллельных прямых;

«> — признаки параллельности прямых;

«> — применение изученной теории к решению задач.

«> Резко очерченных границ между выделенными частями не может быть, последний раздел, безусловно, присутствует во всех предыдущих.

«> Формулировки определений параллельных прямых в учебных пособиях, так же как и подходы к их изучению, различны.

«> В учебном пособии по геометрии А.В. Погорелова и в пробном учебнике Л.С. Атанасяна рассматриваются только два случая взаимного расположения прямых на плоскости: прямые пересекаются (имеют только одну общую точку) и прямые не пересекаются (совсем не имеют общих точек). Поэтому и определения параллельных прямых в этих пособиях даются соответствующим образом:

«>Опр. Две прямые называются параллельными, если они не пересекаются.

«>Опр. Прямые на плоскости не имеющие общих точек называются параллельными.

«> Эти определения параллельных прямых на плоскости эквивалентны друг другу.

«> В учебном пособии по геометрии под редакцией А.Н. Колмогорова рассматриваются три случая взаимного расположения двух прямых на плоскости:

«> — прямые имеют только одну общую точку;

«> — прямые совпадают (все точки общие);

«> — прямые совсем не имеют общих точек.

«> Два последних случая входят в определение параллельных прямых в этом учебнике.

«>В процессе работы над определением параллельных прямых следует особо выделить, что они лежат в одной плоскости, и требовать этого постоянно от учащихся; такая работа поможет избежать нежелательных ошибок в дальнейшем при изучении соответствующих вопросов в курсе стереометрии. В качестве контр примера полезно наглядно показать прямые пространства, которые не лежат в одной плоскости, не имеют общих точек и не являются параллельными (скрещивающиеся прямые).

«>Две прямые называются параллельными, если они:

«>2) не пересекаются.

«>1) лежат в одной плоскости;

«>2) не имеют общих точек.

«>1) лежат в одной

«>2) не имеют общих точек.

«> Аксиома. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Существование параллельных прямых обосновывается в школе двумя путями, а именно на основе центральной симметрии или на основе свойств углов, образованных при пересечении двух прямых третьей.

«> Доказательство теоремы везде ведется методом от противного. Однако предложения, на основе которых делается окончательный вывод, различны: в одних случаях это свойство двух различных прямых не иметь двух и более различных общих точек; в других случаях это свойство внешнего угла треугольника не быть меньшим или равным внутреннему углу этого треугольника, не смежному с ним. Доказательство теоремы опирается на представление учащихся о неограниченности и бесконечности прямой, что сопряжено с большими трудностями, связанными с потерей наглядности чертежа, противоречием правильным интуитивным представлениям учащихся.

«>Вследствие этого чертежу желательно уделить особое внимание при доказательстве теоремы, при изображении точки пересечения прямых желательно не делать изломов.

«>Теоремы — признаки параллельности прямых требуют тщательной методической разработки, их доказательство надо сопровождать соответствующими записями. В качестве примера рассмотрю соответствующую теорему по учебному пособию под редакцией А.Н. Колмогорова:

«> Запись этой теоремы с ее доказательством может

«>выглядеть следующим образом:

«> Признак параллельности прямых.

«> Дано: прямые а и b, b=Z0(a).

«> Доказательство(метод от противного)

«> 1. Пусть а и b различны и

«> непараллельные, т.е. а и b имеют

«> 2. С отлична от O, так как b и

«> 3. С и Z0(C)=C1 различны, так как С не совпадает с О.

«> 4. C1 принадлежит прямым а и b, так как С принадлежит этим прямым.

«> 5. Прямые а и b имеют две различные общие точки С и C1, что

«> 6. Предположение, что а и b непараллельные, неверно. Значит, а и b параллельны.

«> 7. Если а и b центрально-симметричны и совпадают то они параллельны, по определению.

«>Раздел об углах, образующихся

«>при пересечении двух прямых третьей.

«> Рисунок к введению этих понятий

«>не должен отражать частных случаев: две

«>прямые не должны изображаться параллельными,

«>а секущая не должна быть к ним перпендикулярной (рис-2).

«> Прямые а и b разбивают плоскость на три части: две внешние и одну внутреннюю.

«> Из восьми углов, образующихся при пересечении прямых а и b прямой с, некоторые лежат по одну сторону от прямой с, другие по разные стороны от прямой с. Некоторые из углов, расположенных по разные стороны от прямой с, получили название накрест лежащих;

«>некоторые углы, расположенные по одну сторону от прямой с, получили название или односторонних или соответственных. В зависимости от того, в каких из названных частей расположены углы, различают внутренние и внешние накрест лежащие углы (3 и 6, 4 и 5, 1 и 8, 2 и 7), внутренние или внешние односторонние углы (4 и 6, 3 и 5, 1 и 7, 2 и 8), соответственные углы (2 и 6, 1 и 5, 4 и 8, 3 и 7).

«> Большую роль в изучении параллельных прямых играет аксиома параллельных прямых.

«> В имеющейся учебной литературе приведены различные формулировки аксиомы параллельных:

«>1.Аксиома. Через данную точку проходит не более одной прямой, параллельной данной прямой.

«>2.Аксиома. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

«> 3.Аксиома. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной .

«> Требование, чтобы точка не лежала на данной прямой, связано с тем, что в этих учебных пособиях совпадающие прямые не считаются параллельными и вообще не рассматриваются. Надо отметить, что в третьем случае аксиома является более сильной, чем в первом и во втором случае. Утверждение, что через точку проходит только одна прямая, параллельная данной прямой, в первом случае можно доказать:

«> Следовательно, через данную точку проходит только одна прямая, параллельная данной прямой. Эти рассуждения приводятся не во всех учебных пособиях для средней школы.

«> В процессе изучения параллельности прямых весьма важно обращать внимание на раскрытие роли аксиомы параллельности при построении темы. При доказательстве соответствующих теорем, где явно используется аксиома параллельных, этот пункт доказательства

«>желательно особо выделить.

«>Теорема. Две прямые, параллельные третьей, параллельны. .

«>Дано: а, b и с — прямые, а││с и b││с.

«> Доказательство (рис. 3).

«> 1. Пусть прямые а и b не параллельны, т.е. а и b пересекаются в некоторой точке С.

«> 2. Через точку С проходят две прямые а и b, параллельные прямой С, что противоречит аксиоме параллельных.

«> 3. Предположение, что прямые а и b не параллельны, неверно. Значит, а││b. Ч.т.д.

«>При изложении курса геометрии большое значение имеют как

«>теоремы — признаки параллельности, так и теоремы, им обратные.

«>Достаточно доказать один из признаков параллельности прямых, основанных на углах, образованных при пересечении двух прямых третьей, а остальные признаки параллельности свести к уже доказанному.

«> Особый интерес представляет методика работы над теоремами — признаками параллельности прямых в соответствии с учебным пособием по геометрии А.В. Погорелова и пробным учебником по геометрии Л.С. Атанасяна (Рис-4):

«>Дано: с — секущая для прямых а и b;

«> угол 1 и угол 2 — внутренние накрест лежащие; 1=2.

«> Доказательство: (метод от противного).(Таблица-2)

«> Доказательства признака параллельности прямых

«>По учебному пособию

«>По пробному учебнику

«> т.е. пересекаются в точке с.

«>Точку Е на прямой b.

«>3. ∆ВАD=∆АВС по первому признаку

«>4. ABD=BAC, так как

«>5. ABE=BAC, так как 1=2.

«>6. ABD=ABE как равные одному и тому же ВАС.

«>7. Лучи BD и BE совпадают, так как ABD=ABE (аксиома откладывания углов)

«>8. D принадлежит прямой b, так как лучи BD и BE совпадают.

«>9. Прямые а и b имеют две различные общие точки D и С, что невозможно.

«>10. Предположение, что а и b

«> пересекаются, неверно. Значит, а││b.

«>1. Пусть а и b не параллельны,

«> т.е. имеют общую точку С.

«>2. 2 внутренний в ∆АВС, а

«> 1 внешний в ∆АВС.

«> 1>2 по теореме о внешнем

«>Это противоречит условию

«>4. Предположение, что а и b

«>не параллельны, неверно.

«> Перед доказательством признаков параллельности прямых необходима специальная работа по организации повторения тех вопросов, которые составляют основу доказательства, а именно: Организация повторения вопросов которые составляют основу доказательства признака параллельных прямых.(Таблица-3)

«> Организация повторения вопросов которые составляют основу доказательства признака параллельных прямых

«>По учебному пособию

«>а) признаки равенства

«>треугольников и определение

«>б)аксиома откладывания углов;

«>в) углы, образуемые при пересечении двух прямых третьей;

«>г) свойство смежных углов.

«>а) углы, образуемые при пересечении двух прямых третьей;

«>б) нахождение на рисунке внутренних углов треугольника и внешних его углов;

«>в) нахождение на рисунке внутренних углов треугольника, не смежных с данным внешним его углом;

«>г) свойства внешнего угла треугольника.

«>Повторение проводится по рисункам, при этом предполагается их варьирование во избежание частных случаев.

«> По содержанию задачи по этой теме можно разделить на три группы:

«> 1) Задачи на прямое применение аксиомы параллельности:

«> 2) Задачи на применение признаков параллельности прямых:

«> 3) Задачи на применение теорем, обратных признакам

«>параллельности прямых: «Через вершину А треугольника АВС проведена

«>2. Параллельность прямых в пространстве. Скрещивающиеся прямые

«> Учение о параллельности прямых в курсе стереометрии можно разделить на следующие части.

«> — Определение параллельных и скрещивающихся прямых;

«> — Теорема о параллельных прямых;

«> — Признак параллельных прямых;

«> — Применение изученной теории к решению задач.

«> Определения параллельных и скрещивающихся прямых в обоих учебниках звучат одинаково и являются ключевыми во всей теме, но вводятся они по разному (Таблица-4 ). В учебнике А.В. Погорелова определение параллельных и скрещивающихся прямых дается сразу в течении первого урока, а в учебнике Л.С. Атанасяна на первом уроке дается определение параллельных прямых и только после того как пройдет изучение признака параллельных прямых дается понятие скрещивающихся прямых в виде небольшой темы.

«> Определение параллельных и скрещивающихся прямых

«>Опр. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

«>Опр. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.

«>Теорема о параллельных прямых и ее доказательство в обоих

«>учебниках рассматривается на первом занятии и представляется в

«>следующем виде (Таблица-5):

«> Теорема о параллельных прямых и ее доказательство

«>Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну

«>Через любую точку пространства,

«>не лежащую на данной прямой,

«>ходит прямая, параллельная данной и притом только одна

«>1) Пусть а — данная прямая и А — точка, не лежащая на этой прямой. Проведем через прямую а и точку А плоскость z. Проведем через точку А в плоскости z прямую а1, параллельную а. Докажем, что прямая а1, параллельная а, единственна. Рис-а

«>2) Допустим, что существует другая прямая а2, проходящая через точку А и параллельная прямой а. Через прямые а и а2 можно провести плоскость z2.

«>3) Плоскость z2 проходит через прямую а и точку А; следовательно, по теореме (Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну) она совпадает с z

«>4) Теперь по аксиоме параллельных прямые а1 и а2 совпадают. ч.т.д.

«>1) Рассмотрим прямую а и точку М, не лежащую на этой прямой. Через прямую а и точку М проходит плоскость, и притом только одна. Обозначим эту плоскость буквой z.

«>2) Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. должна лежать в плоскости z.

«>3) Но в плоскости z, как известно из курса планиметрии через точку М проходит прямая, параллельная прямой а, и притом только одна. На рис-б эта прямая обозначена буквой b.

«>4) Итак, b-единственная прямая, проходящая через точку М параллельно прямой

«>В учебнике Л.С. Атанасяна разбирается такое понятие, как параллельность трех прямых. И выдается следующие утверждение в виде леммы.

«> Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

«> Признак параллельных прямых и его доказательство в обоих учебниках рассматривается на втором занятии и представляется в следующем виде (Таблица-6):

«> Признак параллельных прямых.

«>Две прямые, параллельные третей прямой, параллельны.

Параллельные прямые

Вы будете перенаправлены на Автор24

Понятие параллельных прямых

Параллельные прямые – прямые, которые лежат в одной плоскости, не совпадают и не имеют общих точек.

Если у прямых есть общая точка, тогда они пересекаются.

Если все точки прямых совпадают, то имеем по сути одну прямую.

Если прямые лежат в разных плоскостях, то условий их параллельности несколько больше.

При рассмотрении прямых на одной плоскости можно дать следующее определение:

Две прямые на плоскости называют параллельными, если они не пересекаются.

Зачастую рассматривается понятие параллельных отрезков.

Два отрезка называют параллельными, если они лежат на параллельных прямых.

Например, на рисунке параллельными являются отрезки $AB$ и $CD$, т.к. они принадлежат параллельным прямым:

Вместе с тем, отрезки $MN$ и $AB$ или $МN$ и $CD$ параллельными не являются. Этот факт можно записать с помощью символов следующим образом:

Готовые работы на аналогичную тему

$MN ∦ AB$ и $MN ∦ CD$.

Аналогичным образом определяется параллельность прямой и отрезка, прямой и луча, отрезка и луча или двух лучей.

Историческая справка

Параллельные прямые в жизни

Зачастую мы не замечаем, что в обычной жизни нас окружает огромное число параллельных прямых. Например, в нотной тетради и сборнике песен с нотами нотный стан выполнен с помощью параллельных линий. Также параллельные линии встречаются и в музыкальных инструментах (например, струны арфы, гитары, клавиши фортепиано и т.п.).

Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно. Рельсы линий метро и железных дорог располагаются параллельно.

Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий.

Параллельные прямые в архитектуре

На представленных изображениях архитектурные сооружения содержат параллельные прямые. Использование параллельности прямых в строительстве помогает увеличить срок службы таких сооружений и придает им необычайную красоту, привлекательность и величие. Линии электропередач также умышленно проводятся параллельно, чтобы избежать их пересечения или соприкосновения, что привело бы к замыканию, перебоям и отсутствию электричества. Чтобы поезд мог беспрепятственно перемещаться рельсы также выполнены параллельными линиями.

В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Читайте также: