Разбиение множества на классы реферат
Обновлено: 05.07.2024
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х , Х ,…, Х , если:
1) подмножества Х, Х,…, Х попарно не пересекаются;
2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
- математика: логика
- теория множеств и комбинаторика
Разбиение множества на классы ( реферат , курсовая , диплом , контрольная )
Два множества, содержащих одинаковые элементы, называются пересекающимися. В этом случае говорят, что множества пересекаются.
Два множества, нс имеющих общих элементов, называются непересекающимися. В этом случае говорят, что множества не пересекаются.
Пример 6.3.1. Множества , нс псрссскаются.
Непересекающимися являются множество треугольников и множество параллелограммов.
Также нс псрссскаются множества решений уравнений * 3 =3* 2 и *+3=0. •.
Пример 6.3.2. Пусть А - множество треугольников, площадь которых равна 6, В — множество прямоугольных треугольников.
А и В — пересекающиеся множества, так как существует треугольник, являющийся одновременно элементом множеств А и В, например треугольник со сторонами 3, 4, 5. Он прямоугольный и имеет площадь.
равную 6 (проверьте эти утверждения). Этот пример нс единственен. Приведите пример еще одного такого треугольника.
Пересекаются также множества решений уравнений х 2 +х=0 и х 2 -х=0, так как оба эти множества содержат число 0. •.
Пример 6.3.3. Множества , и не пересекаются в совокупности, то есть нет ни одного элемента, который принадлежал бы каждому из множеств. Однако любая пара этих множеств имеет общий элемент. •.
Пусть дана совокупность множеств. Говорят, что множества этой совокупности попарно не пересекаются, если никакие два (различных) множества совокупности нс псрссскаются.
Пример 6.3.4. Множества , , и попарно не пересекаются. •.
Два множества могут находиться в следующих отношениях:
- 1) множества могут быть пересекающимися,
- 2) множества могут быть нспсрссскающимися,
- 3) множества могут быть связаны отношением включения.
Пример 6.3.5. Рассмотрим два предложения:
Ясно, что РФ (). Оказывается, обратное утверждение в общем случае тоже неверно, то есть ()ФР. Контрпример: Л=0, В — любое. Как известно, 0сЯ, но это непересекающиеся множества.
Если же исключить случай пустого множества, то Q => Р. Действительно, берем любой элемент а из А. Так как A то аеВ. Значит, а общий элемент множеств А и В. •
Теперь введем важное понятие разбиения множества на классы (21, "https://referat.bookap.info").
Пусть дана система К непустых подмножеств некоторого множества S. Говорят, что множества системы К образуют разбиение множества 5, если выполняются два условия:
- 1) подмножества попарно не пересекаются;
- 2) каждый элемент множества S лежит в некотором подмножестве.
Подмножества системы К называются классами разбиения. Количество классов может быть любым, в том числе бесконечным.
Вначале ограничимся примерами разбиений на конечное число классов.
Пример 6.3.6. Множества всех четных чисел х2> = и всех нечетных чисел пеZJ образуют разбиение множества Z на два класса.
Множество всех простых чисел, множество всех составных чисел и множество образуют разбиение множества N на три класса.
Множество всех положительных чисел, множество всех отрицательных чисел и множество
Пример 6.3.7. Докажем, что множество всех треугольников можно разбить на три класса:
А — множество остроугольных треугольников (треугольник называется остроугольным, если все его углы острые);
А-у — множество прямоугольных греугольников (треугольник называется прямоугольным, если он имеет прямой угол);
Аз множество тупоугольных треугольников (треугольник называется тупоугольным, если он имеет тупой угол).
Действительно, каждый треугольник относится к одному из рассмотренных видов. При этом никакие два класса нс пересекаются. А нс пересекается ни с каким классом по определению. Покажем отсутствие общих элементов у множеств Л2 и А3. Предположим, что в треугольнике есть прямой угол и тупой угол. Тогда их сумма будет больше 180 фадусов, поэтому сумма всех трех углов треугольника будет больше 180 градусов. А эго противоречит теореме о сумме углов rpeyi ольника. •.
Пример 6.3.8. Разобьем множество всех десятичных цифр на 4 класса. Это можно сделать разными способами.
Подсчет числа всех разбиений л-элементного множества на определенное число классов является непростой задачей и решается средствами комбинаторного анализа.
При построении второго разбиения в примере мы использовали следующий принцип: вначале записали все цифры, кратные 4 (это числа вида 4/г), затем все цифры, дающие при делении на 4 остаток I (числа вида 4л+1), далее те цифры, которые дают остаток 2 (числа вида 4л+2) и, наконец, цифры, дающие остаток 3 (числа вида 4л+3).
Указанный принцип позволяет разбить на 4 класса все множество целых или натуральных чисел, при этом классы будут являться бесконечными множествами.
Теперь рассмотрим пример разбиения на бесконечное множество классов.

Пример 6.3.9. Возьмем числовую прямую. Тогда целые числа разделят прямую на промежутки. Однако это еще не совсем разбиение, нужны уточнения. Если рассмотреть отрезки, то, например, [2; 3] и [3; 4] будут иметь общий элемент 3. Не включить целые числа означает разбить не все множество R. Поэтому отнесем целое число к одному из концов промежутка, например к правому. Получим семейство промежутков вида (я;л+1], п — целое число.
Итак, семейство множеств К= образует разбиение множества R действительных чисел на классы.
Приведенный пример разбиения множества R на бесконечное число классов не единственен. Например, можно считать множество Z целых чисел отдельным классом, а все другие классы — это интервалы вида (л; п+1). Есть и другие примеры разбиений. •.
Заметим, что любая классификация вещей, процессов или понятий приводит к соответствующим разбиениям.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
КАРТА – СХЕМА УЧЕБНОГО ЗАНЯТИЯ
продолжительность - 90 минут
Тема занятия: Декартово произведение и разбиение множеств на классы
Цели занятия:
расширить знания студентов с темы действия с множествами, рассмотреть Декартово произведение, разбиение множеств на классы;
способствовать развитию памяти, внимания, логического мышления;
создать условия для применения полученных знаний при выполнении расчетных заданий.
Необходимое аппаратное и программное обеспечение:
Дидактическое обеспечение:
Карточки с заданиями самостоятельной работы
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. - 4-е изд., стер. - М. : Издательский центр "Академия", 2014.
Информационные источники:
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. - 4-е изд., стер. - М. : Издательский центр "Академия", 2014.
Тип и вид учебного занятия:
ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА
Этапы урока
Содержание и виды деятельности преподавателя
1. Организационный этап
Приветствие, выявление отсутствующих, информирование о теме и целях занятия.
2. Актуализация ЗУН
- Что такое множество? Что означает задать множество?
- Способы задания множеств
- Что такое подмножество?
-какие действия выполняем над множествами?
- Что такое пересечение? Объединение?
- Какие свойства пересечения, объединения?
Самостоятельная работа (с взаимопроверкой)
Найдите: а) А∩В; б) А∩С; в) С∩В.
Найдите: а) АUВ; б) АUС; в) СUВ.
Найдите а)(А∩В)∩С; б) )(АВ)С; в) (А В)∩С
3. Изучение нового материала
Теоретические сведения.
- разбиение множеств на классы
4. Первичное закрепление
Практическое выполнение заданий
5. Информация о домашнем задании
Методические рекомендации для самостоятельной работы
6. Подведение итогов урока
Подведение итогов работы группы, отдельных студентов.
Корректирование пробелов знаний.
Декартово произведение
В начальных классах ученики решают задачу: используя цифры 1, 2, 3 образовать всевозможные двузначные числа.
Путем перебора дети получают:
Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.
В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные пары (а; b), образованные из элементов а и b. Это (1; 2), (1; 3), (1; 4) и т.д. Первый элемент а называют первой координатой пары, элемент b – второй.
Значит, в нашей задаче мы оперировали множеством А=> и образовывали всевозможные пары.
Рассмотрим другой пример. Пусть А=, B=. Образуем всевозможные пары (а;b) так, что аА, bВ. Получим некоторое новое множество <(1; 5), (1; 4), (2; 4), (2; 5), (3; 4), (3; 5)>, элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств А и В.
Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают АВ. Таким образом АВ = | xA, yB>.
Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.
Рассмотрим следующий пример. Известно, что АВ= . Установим, из каких элементов состоят множества А и В. Так как первая компонента пары декартового произведения принадлежит множеству А, а вторая – множеству В, то данные множества имеют следующий вид: А=, B= 6>.
Перечислим элементы, принадлежащие множеству АВ, если
А= d>, B=A. Декартово произведение АВ=<(a, a), (a, b), (a, c),
(a, d), (b, a), (b, b), (b, c), (b, d), (c, a), (c, b), (c, c), (c, d), (d, a), (d, b) ,(d, c), (d, d)>.
Количество пар в декартовом прoизведении АВ будет равно произведению числа элементов множества А и числа элементов множества В: n(АВ)=n(A)n(B).
В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента.
Используя понятие кортежа, можно определить понятие декартового произведения n множеств.
Декартовым произведением множеств А, А,…, A называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А, вторая – А, …, n-ая – множеству А: АА…A.
Пусть даны множества А=; А=; A=. Декартово произведение ААА=< (2, 3, 7), (2, 3, 8), (2, 4, 7), (2, 4, 8), (2, 5, 7),
(2, 5, 8),(3, 3, 7), (3, 4, 7), (3, 3, 8), (3, 4, 8), (3, 5, 7), (3, 5, 8)>.
Понятие разбиения множества на классы
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х, Х,…, Х, если:
1) подмножества Х, Х,…, Х попарно не пересекаются;
2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Примеры
Приведем несколько примеров разбиения:
1. Множество четырехугольников разбито на два класса:
трапеции и прямоугольники. Данные подмножества попарно не пересекаются, а их объединения совпадают с множеством .
2. Множество четырехугольников разбито на три класса:
квадраты, параллелограммы, прямоугольники. Так как прямоугольник и квадрат – частные случаи параллелограмма, то данные подмножества пересекаются, значит, не выполнено первое условие классификации, и разбиение множества не получено.
3. Дано множество прямых в пространстве, которое разбито на классы по их взаимному расположению: параллельные, пересекающиеся, скрещивающиеся. Данные подмножества попарно не пересекаются, а их объединения совпадают с множеством .
4. Дано множество , которое можно разделить на два класса: и , где – множество натуральных четных чисел, а – множество натуральных нечетных чисел.
5. Множество разбито на три класса: , и . множество чисел, которые делятся на , – множество чисел, которые делятся на , множество чисел, которые делятся на . Но существуют числа, которые могут делится одновременно и на , и . Отсюда следует, что подмножества пересекаются, и разбиение не получено.
Практические задания
Пример 1. Даны множества: А1= , А2= , А3 = . Найти А1´ А2 ´А3.
Решение. Элементами множества А1´ А2 ´А3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству А1, вторая – множеству А2, третья – множеству А3.
Декартово произведение X Х может быть записано в виде множества из упорядоченных пар:
Большое значение для развития мышления ребенка и его практической деятельности имеет умение правильно выполнять классификацию, например, группировать предметы по заданному признаку.
Разбиение множества на классы — это действие распределения объектов по классам на основании сходств объектов внутри класса и их отличия от объектов других классов.
Условия правильной классификации
1. Подмножества (классы) попарно не пересекаются.
2. Объединение всех подмножеств (классов) совпадает с исходным множеством.
Другими словами, классификация будет правильной, если все элементы заданного множества будут распределены по классам и каждый элемент будет находиться только в одном классе.
Классификация применяется во всех науках и в быту. Например, в зоологии классифицируют животных, в ботанике — растения, в школе дети распределяются по классам. Далеко не каждая группировка является классификацией. В педагогике выделение двух видов наглядного материала: демонстрационного и раздаточного не является классификацией, так как один и тот же материал может менять свою функцию. Часто некорректно сформулированное задание ставит человека в затруднительное положение. Например, родители просят дочь: «Положи все книги на две полки: свои - на верхнюю полку, а книги брата — на нижнюю*. Если у детей есть общие или чужие книги, это задание не выполнимо.
Задание 27
1. Определите необходимые условия для правильной классификации в приведенном выше примере с кубиками.
2. Определите, является ли классификацией распределение треугольников на виды:
а) I - равносторонние, 6) I — остроугольные,
II — равнобедренные, II — тупоугольные,
III — разносторонние; III — прямоугольные.
Соответствия между двумя множествами
Изучая окружающий мир, математика рассматривает не только его объекты, но и связи между ними. При выполнении многих математических и бытовых задач устанавливают связи между двумя множествами, которые называют соответствиями. Например:
• Решите уравнения уравнения →числа, которые являются корнями уравнения).
• Измерьте длину отрезков отрезки → числа, характеризующие их длины).
• Сядьте на свои места (люди → стулья).
Одной из начальных задач математической подготовки детей является формирование умения устанавливать соответствия между двумя множествами.
Или такой пример: на пронумерованных стульях разложены куклы: одна, две, ни одной. На рисунке 37 игрушки обозначены буквами А, В, С, D.

• Подбери к каждой картинке соответствующую геометрическую фигуру. (Наглядный материал: карточки с изображением солнышка, конверта, носового платка и геометрические фигуры из картона: круг, квадрат, прямоугольник.)
• Дай белочкам по одной шишечке. (Наглядный материал: картинки или игрушки, количество которых одинаково.)
Ребенок каждому элементу одного множества ставит в соответствие только один элемент другого множества, охватывая все элементы. Такие соответствия называют взаимно однозначными.
Взаимно однозначное соответствие — это соответствие, при котором каждому элементу одного множества соответствует единственный элемент другого множества и каждый элемент второго множества соответствует только одному элементу первого множества.
В процессе формирования счетной деятельности дети учатся устанавливать взаимно однозначное соответствие между отрезком натурального ряда и множеством предметов, которые считают. Отсюда следуют те правила, без которых счет невозможен:

- Каждому предмету соотносить только одно число.
-Каждое число соотносить только одному предмету. Дети, не понимающие этого, совершают ошибки:
• пропускают при счете предметы,
• один и тот же предмет считают дважды,
• одно число повторяют дважды.
Предварительная практическая работа по составлению пар предметов из разных множеств (установление взаимно однозначных соответствий) дает впоследствии возможность осознанно выполнять счет, быстро и правильно сформировать навыки счетной деятельности.
Задание 29
Постройте графы четырех различных соответствий между множествами X = и У = тан, чтобы одно из них было взаимно однозначным.
Равномощные множества
Пусть даны два множества: А = и В = Не пересчитывая число их элементов, а лишь установив взаимно однозначное соответствие, можно сказать, что множество А содержит элементов столько же, сколько и множество В. Говорят, что эти множества имеют одинаковую мощность, или они равномощны. Пишут А -В.
Множества называются равномощными, если между их элементами можно установить взаимно однозначное соответствие.
Задание 30
Постройте графы взаимно однозначных соответствий, если это возможно, между множествами:
— дней недели и цветов спектра;
— времен года и цветов спектра.
Нетрудно убедиться в том, что если равномощные множества конечны, то они содержат поровну элементов.
Конечные равномощные множества называются равночисленными.
Бесконечные множества могут быть равномощными, например, множество действительных чисел и множество точек прямой, и не равномощными, например, множество натуральных чисел и множество точек прямой.
Задание 31
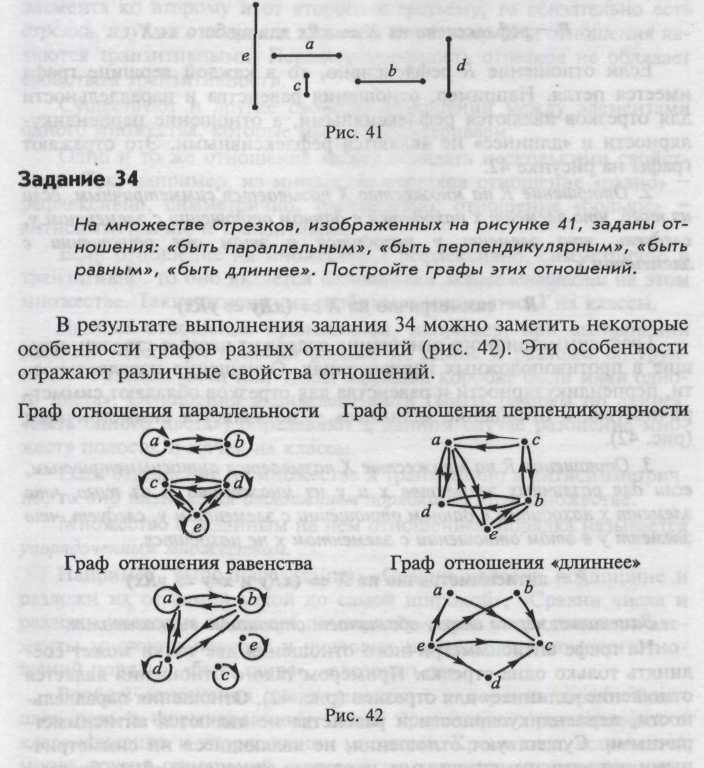
Приведите примеры множеств, равномощных множеству:
— времен года;
— углов у пятиугольника;
— ног у человека.
2.8. Отношения между элементами одного множества
Связи между элементами одного множества в математике называют отношениями.
Отношения очень многообразны, например:
Отношения могут быть заданы и на символическом языке, например, как в задании 32.

2. Перечисляют все пары элементов, взятых из множества и связанных этим отношением.
Полезно предлагать детям упражнения, выполняя которые они переходят от одного способа задания отношений на множестве к другому. Например.
1.Вставьте пропущенное число: (1;6), (8;13), (5;10), (7; 12), (3; . )-Здесь необходимо сначала выяснить характеристическое свойство всех пар чисел, а затем найти пропущенный элемент.
Выполняя данное упражнение, дети должны перейти от задания отношения с помощью характеристического свойства к перечислению пар элементов.
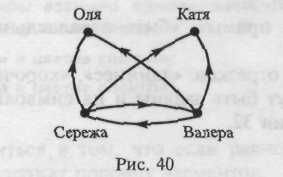
Задание 33
Придумайте различные отношения на множестве одной семьи (мама, папа, их дети — Оля, Катя, Сережа, Валера) и изобразите эти отношения с помощью графов.
В процессе игры или обучения детям постоянно приходится рассматривать элементы одного множества и устанавливать отношения между ними:
• сравнивать по величине;
• подбирать одинаковые по цвету или форме;
• делить на группы.
В математике изучают разнообразные отношения. Чтобы облегчить решение этой задачи, отношения классифицируют по свойствам.

В процессе изучения предметов и явлений окружающего мира мы постоянно сталкиваемся с классификацией. Классификация широко используется в биологии, химии, математике, языке и многих других науках. Она облегчает процесс усвоения знаний.
Классификация в любой области человеческой деятельности связана с разбиением множества на подмножества (классы). Например, классификация частей речи, членов предложения, чисел, геометрических фигур и так далее.
Полученные подмножества должны обладать некоторыми свойствами:
1) они не должны быть пустыми;
2) не должны содержать общих элементов;
3) объединение всех подмножеств должно равняться самому множеству.
Определение: Классификацией или разбиением множества на классы называется представление этого множества в виде объединения непустых попарно непересекающихся своих подмножеств.
Для примера рассмотрим классификацию с помощью двух свойств.
А –множество отличников;

–множество не отличников;
В –множество спортсменов;

–множество не спортсменов.

I I– множество отличников - не спортсменов;
IV– множество не отличников - не спортсменов;
Число элементов объединения и разности двух конечных множеств
Пусть A и B – конечные множества. Число элементов множества A условимся обозначать символом m(A) и называть численностью множества A.
Определим численность объединения множеств A и B.
Если множества A и B не пересекаются (см. рис. 1а), то m(AÈB) = m(A) + m(B). Таким образом, численность объединения конечных непересекающихся множеств равна сумме численностей этих множеств.
Если множества A и B пересекаются (см. рис. 1б), то в сумме m(A) + m(B) число элементов пересечения AÇB содержится дважды: один раз в m(A),а другой – в m(B). Поэтому, чтобы найти численность объединения m(AÈB), нужно из указанной суммы вычесть m(AÇB). Таким образом:
m(AÈB) = m(A) + m(B) - m(AÇB)
Определим теперь численность разности множеств A и B.
Если множества A и B не пересекаются (см. рис. 1а), то A \ B = A, и поэтому m(A\B) = m(A).
Если множества A и B пересекаются (см. рис. 1б), то m(A\B) = m(A) - m(AÇB).
Если В Ì А (см. рис. 1в), то AÇB = B, и, следовательно, m(A\B) = m(A) - m(B).
Читайте также:

