Итеративный метод брауна реферат
Обновлено: 02.07.2024
Также универсальным, но менее трудоемким по сравнению с методом линейного программирования в плане затрат вычислительных ресурсов является приближенный метод Брауна-Робинсона. Данный итерационный метод предназначен для решения любой игры G(m´n), не требуя никаких ограничений на элементы матрицы игры.
Метод базируется на многократном разыгрывании игры и подсчете верхней и нижней оценок цены игры с занесением результатов в таблицу специального вида (табл. 3.11):
| k | i | B1 | … | Bn | j | A1 | … | Am | V | V * |
Каждая строка таблицы соответствует однократному розыгрышу игры (партии игры).
Поясним записи в соответствующих позициях:
· k — номер партии (итерации);
· i и j — номера стратегий, выбранных соответственно игроками A и B в данной партии;
· B1, …, Bn — накопленный за k партий выигрыш игрока A при выборе им стратегии Ai в данной партии и ответе игроком B соответственно стратегиями B1, …, Bn;
· A1, …, Am — накопленный за k партий выигрыш игрока A при выборе игроком B стратегии Bj в данной партии и ответе игроком A соответственно стратегиями A1, …, Am;
· V —нижняя оценка цены игры (минимальный накопленный выигрыш, поделенный на k);
· — верхняя оценка цены игры (максимальный накопленный выигрыш, поделенный на k);
В [6] доказано, что при k à ¥: V * à V, , ,
где V – цена игры, Ni и Nj – число применений соответственно стратегий Аi и Bj за k партий, pi и qj – значения вероятностей в оптимальных стратегиях SA =(pi), i =1, …, m, SB =(qj), j =1, …, n,игроков A и B соответственно.
Проиллюстрируем метод на примере игры G(3´3), представленной табл. 3.12.
| Bj Ai | B1 | B2 | B3 |
| A1 | 7 | 2 | 9 |
| A2 | 2 | 9 | 0 |
| A3 | 9 | 0 | 11 |
Требуется найти решение – пару оптимальных смешанных стратегий (SA, SB), SA =(p1, p2, p3), SB =(q1, q2, q3), и цену игры V.
Будем искать пару смешанных стратегий SA =(p1, p2, p3), p1 + p2 + p3 = 1, SB =(q1, q2, q3), q1 + q2 + q3 = 1 и цену игры V.
Построим табл. 3.13 для первых десяти итераций.
| k | i | B1 | B2 | B3 | j | A1 | A2 | A3 | V | `V | V * |
| 1 | 3 | 9 | 0 | 11 | 2 | 2 | 9 | 0 | 0 | 9 | 4,5 |
| 2 | 2 | 11 | 9 | 11 | 2 | 4 | 18 | 0 | 4,5 | 9 | 6,75 |
| 3 | 2 | 13 | 18 | 11 | 3 | 13 | 18 | 11 | 3,67 | 6 | 4,84 |
| 4 | 2 | 15 | 27 | 11 | 4 | 22 | 18 | 22 | 2,75 | 5,5 | 4,13 |
| 5 | 1 | 22 | 29 | 20 | 3 | 31 | 18 | 33 | 4,0 | 6,6 | 5,3 |
| 6 | 3 | 31 | 29 | 31 | 2 | 33 | 27 | 33 | 4,84 | 5,5 | 5,17 |
| 7 | 1 | 38 | 31 | 40 | 2 | 35 | 36 | 33 | 4,43 | 5,14 | 4,79 |
| 8 | 2 | 40 | 40 | 40 | 2 | 37 | 45 | 33 | 5,0 | 5,61 | 5,30 |
| 9 | 2 | 42 | 49 | 40 | 3 | 46 | 45 | 44 | 4,45 | 5,11 | 4,78 |
| 10 | 1 | 49 | 51 | 49 | 1 | 53 | 47 | 53 | 4,90 | 5,30 | 5,1 |
Поясним процесс заполнения табл. 3.13.
Пусть начинает (k =1) игрок A и выбирает на первом шаге стратегию А1. Его выигрыш в зависимости от выбора игрока B может равняться 9 (при выборе стратегии B1), 0 (при выборе B2) или 11 (при выборе B3). Поскольку теперь выбор за игроком B (а он заинтересован в минимизации выигрыша игрока A), то выделим (жирным шрифтом) минимальный выигрыш 0, соответствующий стратегии B2. Следовательно игроку B выгоднее всего ответить стратегией B2, что, в свою очередь, может привести к выигрышу игрока A при его ответе в следующей партии, равному 2 (при выборе стратегии A1), 9 (A2) или 0 (A3). Так как игрок A заинтересован в максимизации выигрыша, то выделим максимальный выигрыш 9 (для A2). Соответствующие значения V, и V * равны 0; 9 и 4,5.
Во второй партии (k =2) игроку A,следовательно,выгодно выбратьстратегию A2,которая позволит ему накопить выигрыш, равный соответственно 11 (для B1), 9 (для B2) или 11 (для B3) и т.д. Заметим, что для k =4в столбцах А1и А3 получаются одинаковые накопленные выигрыши (22), поэтому игрок A в пятой партии может выбрать как стратегию А1, так и А3.
К сожалению (что видно и по табл. 3.12), сходимость данного метода довольно слабая, но существуют методы ее ускорения. Критерием останова можно выбрать достаточную стабильность величины V * при увеличении числа итераций.
Для рассматриваемого примера в итоге получим:
и , что соответствует точному решению, полученному, например, методом Лагранжа.
Как уже отмечалось, сравнительно невысокая трудоемкость данного метода часто делает его более предпочтительным по сравнению с методом линейного программирования (например, симплекс-методом) при решении задач линейного программирования (после их сведения к соответствующей теоретико-игровой задачи) большой размерности.
Практический пример
Рассмотрим следующую задачу. Проводится конкурс на реализацию двух проектов, в котором участвует два претендента – конструкторское бюро 1 (КБ1), имеющее 4 отдела, и конструкторское бюро 2 (КБ2), имеющее 3 отдела. Финансирование первого проекта – a денежных единиц, второго – b. Практика проведения данного конкурса показывает, что, как правило, проект достаётся тому КБ, которое выделяет большее число отделов на его выполнение. Если каждое КБ выделяет одинаковое число отделов на выполнение проекта, то они имеют одинаковую вероятность на его получение. Требуется определить, сколько отделов следует выделить каждому КБ на выполнение первого и второго проектов с целью максимизации их финансирования.
Если в качестве стратегии КБ взять пару (a, b), где a и b – количество отделов, выделяемых соответственно под первый и второй проекты, то у КБ1 (игрока A) имеется 5 стратегий: A1=(4; 0), A2=(3; 1), A3=(2; 2), A4=(1; 3), A5=(0; 4), а у КБ2 (игрока B) – 4 стратегии: B1=(3; 0), B2=(2; 1), B3=(1; 2), B4=(0; 3).
Так как целью каждого из игроков является максимизация собственного выигрыша (возможного финансирования), то соответствующая парная игра G(5´4)не является антагонистической (выигрыш одного игрока не равен проигрышу другого).
Для того чтобы свести данную игру к антагонистической необходимо из выигрышей aij игрока A вычесть средний выигрыш – (a + b)/2. В итоге получим антагонистическую игру G(5´4), представленную табл. 3.14.
| В1 | В2 | В3 | В4 | |
| А1 | а / 2 | (a – b) / 2 | (a – b) / 2 | (a – b) / 2 |
| А2 | b / 2 | a / 2 | (a – b) / 2 | (a – b) / 2 |
| А3 | (b – a) / 2 | b / 2 | a / 2 | (a – b) / 2 |
| А4 | (b – a) / 2 | (b – a) / 2 | b / 2 | a / 2 |
| А5 | (b – a) / 2 | (b – a) / 2 | (b – a) / 2 | b / 2 |
Рассмотрим случай а = b, представленный табл. 3.15. Упростим игру, удалив доминируемые и дублируемые стратегии A1, A5, B2, B3, A3. Получим игру G(2´2), представленную табл. 3.16.
| Bj Ai | В1 | В2 | В3 | В4 |
| А1 | a / 2 | 0 | 0 | 0 |
| А2 | a / 2 | a / 2 | 0 | 0 |
| А3 | 0 | a / 2 | a / 2 | 0 |
| А4 | 0 | 0 | a / 2 | a / 2 |
| А5 | 0 | 0 | 0 | a / 2 |
| Bj Ai | В1 | В4 |
| А2 | a / 2 | 0 |
| А4 | 0 | a / 2 |
Решив данную игру, например, методом Лагранжа, получим: p2= p4=0,5; q1= q4=0,5; V = a/4.
Тогда для исходной игры G(5´4)решением будет: SA =(0,0; 0,5; 0,0; 0,5; 0,0), SB =(0,5; 0,0; 0,0; 0,5), VКБ1= a / 4 + a =5a / 4, VКБ2=3a / 4.
Математическая теория игр способна не только указать оптимальный путь к решению некоторых проблем, но и прогнозировать их исход. Матричные игры серьёзно изучаются специалистами, так как они довольно просты и к ним могут быть сведены игры общего вида. Поэтому теория матричных игр хорошо развита, существуют различные методы поиска решения игр.
Но в большинстве случаев решение матричных игр представляет собой трудный и громоздкий процесс. Есть примеры, когда даже для матриц размера 3´3, процесс поиска решения довольно трудоёмкий.
Кроме того, выигрыши игроков в каждой ситуации не всегда определяются точными измерениями. В процессе сбора данных об изучаемом явлении, анализа этих данных и введения при построении модели различных предположений накапливаются ошибки. Они же могут выражаться числами в матрице выигрышей. Поэтому точность в определении значения игры и оптимальных стратегий игроков оправдана не всегда.
А также, следует заметить, что погрешность в оценке игроком своего выигрыша не может привести к практически серьёзным последствиям и небольшое отклонение игрока от оптимальной стратегии не влечёт за собой существенного изменения в его выигрыше.
Поэтому возникает потребность в разработке численных методов решения матричных игр. В настоящее время в теории игр известны несколько способов приближенного решения матричных игр.
Цель выпускной квалификационной работы изучить некоторые методы приближённого решения матричных игр, обосновать их алгоритмы, и, по возможности, реализовать на языке программирования.
Работа состоит из введения, трёх параграфов и приложения, в котором приведена программа на языке TurboPascal, позволяющая находить приближённое решение матричной игры.
В первом параграфе приведены основные понятия и утверждения теории матричных игр.
Параграф второй посвящён изложению приближённого решения игры методом Брауна-Робинсона (метод фиктивного разыгрывания) и его обоснованию. Приведён пример применения алгоритма для конкретной матричной игры.
В третьем параграфе рассмотрен ещё один метод – монотонный итеративный алгоритм приближённого решения матричных игр.
§1. Основные понятия
Будем рассматривать только парные антагонистические игры, т. е. игры в которых участвуют только два игрока – две противоборствующие стороны и выигрыш одного из игроков равен проигрышу другого. Кроме того, будем считать, что каждый игрок имеет лишь конечное число стратегий:
U1 =1 , a2 . am > – множество стратегий первого игрока;
U2 =1 , b2 , . bn > – множество стратегий второго игрока.
Будем называть эти стратегии чистыми в отличие от смешанных, которые будут введены далее.
Множество U1 ×U2 – декартово произведение множеств стратегий игроков называется множеством ситуаций в игре. Для каждой ситуации должен быть определён итог игры. Так как игра антагонистическая достаточно определить выигрыш а одного из игроков, скажем первого. Тогда выигрыш второго игрока будет равен (-а ). Таким образом, имеем матрицу выигрышей первого игрока ( для второго игрока матрица выигрышей будет -А):
A=
Определение. Система Г= U 1 , U 2 , A > называется матричной игрой двух лиц.
Разыгрывание матричной игры сводится к выбору игроком 1 i-ой строчки матрицы выигрышей, а игроком 2 - j-го столбца. После этого игрок 1 получает выигрыш равный а ij , а игрок 2 – (-а ij ).

При правильной игре игрок 1 может всегда гарантировать себе выигрыш, который назовём нижним значением цены игры. Обозначим его: .
В свою очередь, игрок 2 может гарантировать себе проигрыш, который назовём верхним значением цены игры. Обозначим его:

.

Чистые стратегии i * и j * , соответствующие называются максиминной и минимаксной стратегиями.

Лемма 1. В матричной игре . [17]
Определение. Ситуация ( i * , j * ) называется ситуацией равновесия, если для i Î 1,2,…, m , j Î 1,2,…, n выполняется неравенство:

.
Ситуация равновесия это такая ситуация, от которой ни одному из игроков не выгодно отклоняться. В этом случае стратегии i * , j * называют оптимальными стратегиями игроков.

Чтобы такая ситуация существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е. .[17]

Определение. Пусть( i * , j * ) - ситуацией равновесия в матричной игре. Тогда число называется значением или ценой игры.

Например, в игре ГА с матрицей А= существует не одна ситуация равновесия. В данной игре их две: (1, 1) и (1, 3).
Множество всех ситуаций равновесия в матричной игре обозначим через Z(Г).
Лемма о масштабе 1. Пусть Г и Г / - две матричные игры с матрицей выигрышей А= aij > и A / = a / ij >, причём А / = b А+ a , b = const , a = const .
Тогда Z (Г)= Z (Г / ) и n / = b n + a (где n / - значение цены игры Г / , n - значение цены игры Г). [17]
Эта лемма имеет большое практическое значение, так как большинство алгоритмов для решения матричных игр основано на предположении, что матрица игры положительна. В случае, когда матрица имеет неположительные элементы, следует прибавить ко всем элементам матрицы число наибольшее по абсолютной величине, из всех отрицательных элементов.
Существуют игры, в которых ситуации равновесия в чистых стратегиях не существует. Тогда игрокам бывает не выгодно придерживаться своих минимаксных и максиминных стратегий, так как они могут получить больший выигрыш, отклонившись от них. В этом случае игрокам разумно действовать случайно, т. е. выбирать стратегии произвольно и не сообщать о выборе сопернику. Такие стратегии игроков будем называть смешанными.
Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.
Так если игрок 1 имеет m чистых стратегий, то его смешанная стратегия x – это набор чисел x =( x 1 , x 2 ,…, xm ), которые удовлетворяют соотношениям , =1. Аналогичным образом определяется смешанная стратегия y игрока 2.
Определение. Оптимальными стратегиями игроков называются стратегии, которые при многократном повторении обеспечивают игрокам максимально возможный средний выигрыш (или минимально возможный средний проигрыш).
Таким образом, процесс игры при использовании игроками своих смешанных стратегий превращается в случайное испытание, которое назовём ситуацией в смешанных стратегиях. Она обозначается так ( x , y ), гдеx и y – смешанные стратегии игроков 1 и 2 соответственно.

Для ситуации в смешанных стратегиях каждый игрок определяет для себя средний выигрыш, который выражается в виде математического ожидания его выигрышей:.

От матричной игры пришли к новой игре =, где X, Y – множества смешанных стратегий игроков, а K – функция выигрышей в смешанных стратегиях. Такую игру называют смешанным расширением матричной игры.
Цели игроков остаются прежними: игрок 1 желает получить максимальный выигрыш, а игрок 2 стремится свести свой проигрыш к минимуму. Поэтому для смешанного расширения игры, аналогичным образом определяются верхнее и нижнее значение цены игры, только теперь игроки выбирают свои смешанные стратегии. Обозначим их:


В этом случае остаётся справедливой лемма 1, т. е..
Определение. Ситуация ( x * , y * ) в игре образует ситуацию равновесия, если для всех x Î X , y Î Y выполняется равенство:
K ( x , y * )≤ K ( x * , y * )≤ K ( x * , y ).

Чтобы ситуация равновесия в смешанном расширении игры существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е. , где n - цена игры.
Для случая смешанного расширения игры также справедлива лемма о масштабе.
Лемма о масштабе 2.
Пусть ГА и ГА / - две матричные игры А / = a А+ В, , a = const , В – матрица с одинаковыми элементами b , т. е. b ij = b для всех i , j .

Тогда Z ()= Z (ГА / ) и n А / = a n А + b (где n А / - значение цены игры ГА / , n А - значение цены игры ГА ). [17]
Теорема. В смешанном расширении матричной игры всегда существует ситуация равновесия. [17]
§2. Итеративный метод Брауна-Робинсона (метод фиктивного разыгрывания)
Часто в практических задачах нет необходимости находить точное решение матричной игры. Достаточно найти приближённое решение, которое даёт средний выигрыш, близкий к цене игры и приближённые оптимальные стратегии игроков.
Ориентировочное значение цены игры может дать уже простой анализ матрицы выигрышей и определение нижней и верхней цен игры. Если они близки, то поисками точного решения заниматься не обязательно, так как достаточно выбрать чистые минимаксные стратегии. Если же они не близки, можно получить приемлемое для практики решение с помощью численных методов решения игр, из которых рассмотрим метод итераций.
Пусть разыгрывается матричная игра ГА с матрицей А=ij > размера (m´n). Идея метода – многократное фиктивное разыгрывание игры с заданной матрицей. Одно разыгрывание игры будем называть партией, число которых неограниченно.
В 1-ой партии оба игрока выбирают совершенно произвольные чистые стратегии. Пусть игрок 1 выбрал i-ю стратегию, а игрок 2 – j-ю стратегию. Во второй партии игрок 1 отвечает на ход игрока 2 той своей стратегией, которая даёт ему максимальный выигрыш. В свою очередь, игрок 2, отвечает на этот ход игрока 1 своей стратегией, которая обращает его проигрыш в минимум. Далее третья партия.
С ростом числа шагов процесса смешанные стратегии, которые приписываются игрокам, приближаются к их оптимальным стратегиям. Этот процесс приближённого нахождения оптимальных стратегий игроков называется итеративным , а его шаги – итерациями.
Итак, предположим, что за первые kразыгрываний игрок 1 использовал i-ю чистую стратегию i k раз (i=1,…,m), а игрок 2 j-ю чистую стратегию раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы .
Игрок 1 следит за действиями игрока 2 и с каждым своим ходом желает получить как можно больший выигрыш. Поэтому в ответ на применение игроком 2 своей смешанной стратегии y k , он будет использовать чистую стратегию ik +1 , которая обеспечит ему лучший результат при разыгрывании (k+1)-ой партии. Игрок 2 поступает аналогично. В худшем случае каждый из них может получить:

где - наибольшее значение проигрыша игрока 2 и - наименьшее значение выигрыша игрока 1.
Рассмотрим отношения, которые определяют средние значения проигрыша игрока 2 и выигрыша игрока 1:

Пусть ν - цена матричной игры ГА . Её значение будет больше выигрыша игрока 1, но меньше проигрыша игрока 2, т. е.

. (1)
Таким образом, получен итеративный процесс, позволяющий находить приближённое решение матричной игры, при этом степень близости приближения к истинному значению игры определяется длиной интервала

.
Сходимость алгоритма гарантируется следующей теоремой.

Теорема. .
Лемма. Для всякой матрицы А и " e > 0 существует такое k 0 , что

.
При предельном переходе в неравенстве (1) при k®¥имеем:

. (2)
Отсюда получаем оценку разности пределов:

.
Из леммы следует, что

.

На основании неравенства (1) имеем: .
Следовательно, в силу ограниченности пределов

.
Получаем оценку для разности пределов:

для "e>0.

Можем заключить, что . Осталось показать равенство пределов n . Это следует из неравенства (2).

Итак, .
Пример. Найти приближённое решение игры с матрицей

А=.
Пусть игру начнёт игрок 2. Он произвольно выбирает одну из своих чистых стратегий. Предположим, что он выбрал свою 1-ю стратегию, а игрок 1 отвечает своей 2-й стратегией. Занесём данные в таблицу.
проигрыш игрока 2
при его стратегиях
В столбце u находится наибольший средний выигрыш 4 игрока 1, полученный им в первой партии; в столбце w стоит наименьший средний проигрыш 1, полученный игроком 2 в первой партии; в столбце n находится среднее арифметическое n=(u+w)/2=5/2, т. е. приближенное значение цены игры, полученное в результате проигрывания одной партии.
Так как игрок 1 выбрал 2-ю стратегию, то игрок 2 может проиграть:
4, если применит свою 1-ю стратегию;
1, если применит свою 2-ю стратегию;
2, если применит свою 3-ю стратегию.
Поскольку он желает проиграть как можно меньше, то в ответ применит свою 2-ю стратегию.
Тогда первый игрок получит выигрыш равный 3, 1, 0 соответственно при своих 1-й, 2-й, 3-й стратегиях, а его суммарный выигрыш за две партии составит:
0+3=3 при его 1-й стратегии;
4+1=5 при его 2-й стратегии;
2+0=2 при его 3-й стратегии.
Из всех суммарных выигрышей наибольшим является 5, который получается при 2-й стратегии игрока 1. Значит, в этой партии он должен выбрать именно эту стратегию.
При 1-й стратегии игрока 1 игрок 2 проигрывает 4, 1, 2 соответственно 1-й, 2-й, 3-й его стратегиям, а суммарный проигрыш за обе партии составит:
4+4=8 при его 1-й стратегии;
1+1=2 при его 2-й стратегии;
2+2=4 при его 3-й стратегии.
Все полученные данные занесём в таблицу. В столбец u ставится наибольший суммарный выигрыш игрока 1 за две партии, деленный на число партий, т. е. 5/2; в столбец w ставится наименьший суммарный проигрыш игрока 2, деленный на число партий, т. е. 2/2; в столбец n ставится среднее арифметическое этих значений, т. е. 7/2.

В наше время существует достаточно большое количество задач, решение которых в аналитическом виде или невозможно в принципе в элементарных функциях, либо связано с большим объёмом работы, что чревато большим временем расчётов и может быть критичным в современном динамичном мире. В такой ситуации остро встаёт вопрос поиска методов решения, используя которые мы можем находить компромисс между временем получения ответа и точностью вычислений. К таким методам в теории игр относится и метод Брауна-Робинсон – итерационный алгоритм поиска частных оптимальных стратегий игроков А и В.
В данном домашнем творческом задании мы рассмотрим теоретические основы данного метода, постараемся доказать условие остановки алгоритма и достижения заданной точности, а также обсудим вопрос сходимости данного метода.
В практической части мы реализуем метод Брауна-Робинсона в среде Matlab и решим две задачи – одну задачу разберём достаточно подробно, занеся процесс решения в специальную таблицу и проверив, являются ли полученные нами смешанные стратегии игроков оптимальными с заданной точностью. Вторую задачу мы наполним смысловым содержанием и постараемся взять платёжную матрицу достаточно большой размерности, чтобы провести анализ зависимости времени вычислений и количества итераций от заданной точности, сделаем вывод о сходимости и применимости данного метода при решении реальных задач.
- Теоретическая справка по методу Брауна-Робинсон
Зачастую на практике при решении задач на антагонистические игры мы сталкиваемся с платёжными матрицами достаточно большого размера, которые невозможно решить ни графическим методом, ни методом Шепли-Сноу по причине большой трудоёмкости. В таком случае имеет смысл использовать метод Брауна-Робинсона, который также называют методом фиктивного разыгрывания или итеративным процессом поиска частного решения в смешанных стратегиях. Данный метод является приблизительным и способен дать решение игры для обоих игроков с определенной степенью точности – той, которую мы заранее зададим. Таким образом, мы можем сами искать баланс между скоростью вычислений и необходимой точностью. Разберём этот метод более подробно.
Предположим, что одна и та же антагонистическая ситуация повторяется многократно и каждый из игроков обладает информацией о предыдущем поведении соперника. Тогда каждый из игроков будет выбирать свою следующую стратегию, опираясь на информацию о смешанной стратегии оппонента, которая вытекает из предыдущих реализаций ситуаций. Таким образом мы получили итеративный процесс выбора стратегий для каждого игрока. Чтобы лучше понять, почему решение, полученное данным методом, будет оптимальным, рассмотрим сначала алгоритм реализаци данного метода. Для данного итерационного метода принципиальное отличие от остальных шагов имеет первый шаг, поэтому мы рассмотрим первые 2 шага и общий k+1 шаг. Для определённости, будем считать, что игрок А первым выбирает стратегию, однако игрок B не знает в рамках одной ситуации, какую стратегию выбрал игрок А.
Шаг 1:
На первом шаге ни один из игроков не знает стратегии другого и выбирает стратегию на основе своих предпочтений, например, для игрока А это может быть максимизация своего среднего выигрыша, а для игрока B – минимизация среднего проигрыша. Таким образом, игрок А выбрал свою чистую стратегию , а игрок B выбрал стратегию .
Шаг 2:
На втором шаге игрок А уже знает, какую стратегию игрок B выбрал на первом шаге и исходит из предположения, что он будет использовать ту же стратегию, что была на предыдущем шаге. Именно поэтому все шаги после первого не отличаются друг от друга – каждый из игроков считает, что его оппонент будет придерживаться той же стратегии, что и на предыдущем шаге, и что на текущем шаге необходимо выбрать такую чистую стратегию, которая бы максимизировала выигрыш (для игрока А) или минимизировала проигрыш (для игрока В) при стратегии оппонента из предыдущего шага. В наших терминах это можно записать следующим образом:
Где – номер чистой стратегии, которую игрок А выбрал на втором шаге. Очевидно, что на втором шаге стратегия каждого из игроков на предыдущем шаге – чистая. Запишем чистую стратегию игрока В на первом шаге в виде смешанной :
– показатель неэффективности стратегии .
Аналогично для игрока B: его стратегия на втором шаге должна минимизировать его потери при стратегии игрока А:
Запишем чистую стратегию игрока А на первом шаге в виде смешанной :
– показатель эффективности стратегии .
K+1 шаг:
Обобщим процедуру выбора стратегии на k+1 шаге и разобъем её на 2 этапа:
Выбор такой чистой стратегии каждым из игроков, которая бы максимизировала (для игрока А) или минимизировала (для игрока B) значение функции выигрыша при смешанной стратегии оппонента на k-ом шаге (Q(k) для игрока А и P(k) для игрока В).
Для игрока А это выглядит следующим образом:
Следовательно, на k+1 шаге игрок А выберет чистую стратегию.
Заметим, что – показатель неэффективности стратегии Q(k).
Следовательно, на k+1 шаге игрок А выберет чистую стратегию.
Заметим, что – показатель эффективности стратегии P(k).
Необходимо определить смешанную стратегию оппонента, изменившуюся в связи с реализацией ситуации на k-ом шаге. Пусть – количество появлений i-ой стратегии на k-ом шаге процесса, а – частота появления i-ой стратегии на k-ом шаге процесса (считаем, что частота эквивалентна вероятности появления i-ого события). Тогда для k+1 значения имеем:
Аналогично пересчитаем частоты для игрока В:
Для k+1 итерации необходимо рассчитать показатель эффективности (для игрока А – ) или показатель неэффективности (для игрока В – ) полученной на k+1 шаге процесса. Очевидно, что при
А общая формула для k+1 шага:
Как будет показано ниже, условием остановки данного алгоритма для достижения точности ε необходимо, чтобы выполнялось неравенство:
Если данное условие не выполняется, необходимо вернуться к 1. и сделать ещё одну итерацию.
Таким образом, мы видим, что данный алгоритм достаточно прост как в понимании, так и в реализации на ЭВМ.
Попробуем ответить на вопрос, почему найденные смешанные стратегии будут решением данной игры. Для начала воспользуемся определением нижней и верхней цен игры, а также теоремой фон Неймана:
(1)
Таким образом, если при некотором будет справедливо, тогда, согласно написанному выше двойному неравенству, V будет ценой игры, а стратегии P(k) и Q(k) будут оптимальными. Таким образом, мы найдем частное решение заданной игры.
С помощью описанного алгоритма мы можем получить две бесконечные последовательности чистых стратегий и , выбранных игроками на основе предположительных смешанных стратегиях и , удовлетворяющих неравенству (1).
Последовательности чистых стратегий, смешанные стратегии которых удовлетворяют условию
(2)
Если последовательность чистых стратегий – разрешающая, то отсюда не следует, что соответствующие им смешанные стратегии сходятся. Однако, если они сходятся:
то стратегии удовлетворяют равенству (2), следовательно, являются оптимальными стратегиями игроков. Таким образом, описанный процесс будет иметь место только при выполнении (2). Утверждение о том, что полученные с помощью описанного алгоритма последовательности чистых стратегий и являются разрешающими, было доказано американским математиком Джулией Робинсон, благодаря чему и была доказана сходимость алгоритма, который мы знаем как алгоритм Брауна-Робинсон.
Последнее, что будет доказано в теоретической части данной работы, – утверждение, что при выполнении (*), мы получим решение с ценой игры, отличающейся от истинной не больше чем на :
Так как и , можно записать, что
– неравенство будет верным (3)
Так как и , можно записать, что
– неравенство будет верным (4)
Тогда в силу того что и :
(5)
(6)
Введём величину , которая стремится к 0 при , в силу того что невозрастаетс ростом k, а неубывает с ростом k.
Если мы поставим условие на (**), то из (5) будет следовать справедливость (3), а из (6) – справедливость (4) при . Теперь умножим (3) на (-1) и сложим с (4):
Итак, мы получили, что некотором k-ом шаге выполняется неравенство (**), из которого следует, что величина будет отличаться от цены игры V не больше чем на .
- Пример использования разработанной программы, решение задачи недружественного поглощения двух компаний и анализ выходных данных
В данном разделе домашнего творческого задания мы рассмотрим решение двух задач с помощью алгоритма Брауна-Робинсон, реализованного в среде Matlab. Код данного алгоритма, реализованного в виде функции, приведен в Приложении. Её входными параметрами являются платежная матрица С и заданная точность ε .
Задача 1.
Приведем решение данной задачи в виде следующей таблицы:
Чистая стратегия игрока А на k-ом шаге
Чистая стратегия игрока B на k-ом шаге
Смешанная стратегия P(k), которая, по предположению игрока B, будет выбрана игроком B на k+1 шаге
Смешанная стратегия Q(k), которая, по предположению игрока А, будет выбрана игроком B на k+1 шаге
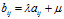
Аффинное правило. Оптимальные стратегии матричных игр, А и В, элементы платежных матриц которых связаны равенством
i=1,m j=1,n, где λ>0, a μ — любое вещественное число, имеют одинаковые равновесные ситуации (либо в чистых, либо в смешанных стратегиях), а цены игр удовлетворяют следующему условию: Ub= λ Ua+μ.
Пусть имеем матричную игру с матрицей, А порядка m x n. Предположим, что цена игры положительна (υ>0). Если это не так, то согласно аффинному правилу всегда можно подобрать такое число μ, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и, следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.
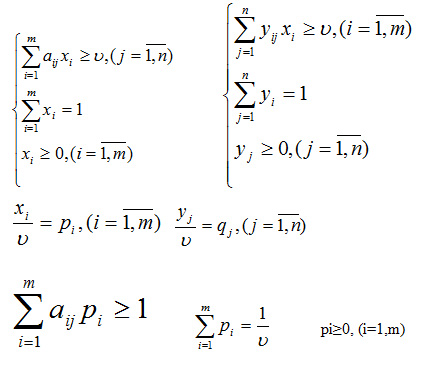
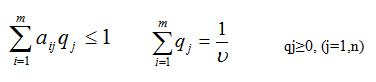
Поскольку первый игрок стремится максимизировать цену игры ? выбором значений xi, то обратная величина 1/ ? должна минимизироваться выбором рi
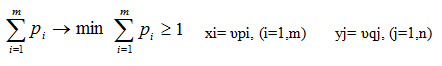
Поскольку второй игрок стремится найти такие значении уj и, следовательно, qj, чтобы цена игры сбыла наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj, при которых

Решение любой матричной игры может быть осуществлено приведением игры к задаче линейного программирования и решением пары двойственных задач. Однако это требует большого объёма вычислений, которое растёт с увеличением числа чистых стратегий игроков (Например, для матрицы 33 имеем систему из 6 неравенств и 2 уравнений).
Поэтому в первую очередь следует, используя метод исключения доминируемых стратегий, уменьшить число чистых стратегий игроков (Исключение не строго доминируемых стратегий может привести к потере некоторых решений. Если же исключаются только строго доминируемые стратегии, то множество решений игры не изменится).
Затем следует проверить наличие Седловой точки. Если в игре есть Седловая точка, то игроки имеют чистые оптимальные стратегии, и решение получается автоматически.
В противном случае хотя бы у одного игрока оптимальные стратегии будут смешанные. Для простых матричных игр, где хотя бы у одного из игроков имеется только 2 стратегии, могут применяться аналитические и графические методы решения. Для более сложных игр необходимо использовать метод приведения игры к задаче линейного программирования.
Итерационный метод
Итерации метода в виде таблицы
| K | i | В | U1(k) | j | А | U2(k) | U(k) | ||||
| В1 | ….. | Вn | А1 | ….. | Аm | ||||||
К — номер партии (итерации)
I — чистые стратегии игрока, А
В1, В2, …, Вn — накопленный выигрыш игрока A при чистых стратегиях B
ύ1 (k) — аналог нижней цены игры (ύ1 (k) = min (В1, В2, …, Вn)/k)
J — чистая стратегия игрока В
A1, A2, …, An — копленный проигрыш игрока A при стратегиях игрока B
ύ2 (k) — аналог верхней цены игры (ύ2 (k) = max (A1, A2, …, An)/k)
ύ(k) — аналог цены игры (ύ(k) = (ύ1 (k) + ύ2 (k)) / 2)
Оптимальные смешанные стратегии игроков определяются частотами выбора чистых стратегий, а в качестве цены игры применяют значение Ню, полученное на последнем шаге.
Данный итерационный процесс сходится, с ростом числа итераций точность решения увеличивается и после достаточного числа итераций можно получить решение с заданной точностью, но скорость сходимости довольна мала. для получения оптимальных стратегий часто необходимо провести 10 или 100 операций. Однако сложность и объем вычислений сравнительно слабо возрастают по мере увеличения числа стратегий игроков.
Для определенности считают, что первый ход делает игрок, А и выбирает свою осторожную стратегию.
Если несколько стратегий игрока дают один и тот же результат, то с т.з. его накопленного выигрыша (проигрыша) выбирается стратегия с меньшим номер.
Оптимальные стратегии игроков определяются частотами выбора их чистых стратегий. Приближенное значение цены игры — результатом ύ(k) на последней итерации.
Читайте также:

