Десять способов решения квадратных уравнений реферат
Обновлено: 02.07.2024
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
X 2 + X = ¾; X 2 - X = 14,5
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
1.2 Как составлял и решал Диофант квадратные уравнения.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 - х. Разность между ними 2х.
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
у 2 - 20у + 96 = 0. (2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
1.3 Квадратные уравнения в Индии
ах 2 + bх = с, а > 0. (1)
В уравнении (1) коэфиценты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).

Соответствующее задаче 13 уравнение:
Бхаскара пишет под видом:
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:
х 2 - 64х + 32 2 = -768 + 1024,
Раздел: Математика
Количество знаков с пробелами: 24847
Количество таблиц: 0
Количество изображений: 17
Похожие работы





. и практическое использование различных форм уроков математики Для того чтобы доказать или опровергнуть, что использование различных форм уроков способствует улучшению качества знаний школьников по теме "Квадратные уравнения", были разработаны и проведены разнообразные формы уроков в 8 классе МОУ “Иштеряковская средняя общеобразовательная школа". При изучении темы были выбраны такие формы .
. на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта .
. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня. Глава 1. История квадратных уравнений и уравнений высших порядков 1.1 Уравнения в Древнем Вавилоне Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная .
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа № 1
Научно-исследовательская работа
Тема:Решение квадратных уравнений различными способами.
Предмет: алгебра
Выполнила: Ученица 8 Б класса
Пешкова Оксана Ильинична
Объектисследования: квадратные уравнения.
Предметисследования: способы решения квадратных уравнений.
Цель: Изучить теоретические основы квадратных уравнений и способов их решении; рассмотреть применение данных способов решения квадратных уравнений на конкретных примерах.
1) Произвести анализ учебно–методической литературы по решению квадратных уравнений.
2) Произвести анализ различных способов решения квадратных уравнений
3)Изучить историю развития квадратных уравнений.
4) Изучить различные способы решения квадратных уравнений и апробировать материал на практике.
Гипотеза: любое квадратное уравнение можно решить всеми существующими способами
Обоснование: Уравнения - это наиболее объёмная тема всего курса математики. Данная работа является попыткой обобщить и систематизировать изученный материал по выше указанной теме. В него вошли как известные нам из школьного курса алгебры способы решения квадратных уравнений, так и дополнительный материал.
Методы исследования:
Теоретические методы: изучение литературы по теме исследования
Анализ информации, полученной при изучении литературы; анализ результатов, получены при решении квадратных уравнений различными способами.
Сравнение способов на рациональность их использования при решении квадратных уравнений.
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
Выбор этой темы основывался на том, что уравнения есть как в программе начальной, так и в каждом последующем классе общеобразовательных школ, лицеев, колледжей. Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.
Квадратное уравнение представляет собой большой и важный класс уравнений, решающих как с помощью формул, так и с помощью элементарных функций.
В учебниках мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем решение по формулам. Вместе с тем, современные научно – методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.
Выбор способа должен оставаться за учащимся. Каждый ученик должен уметь верно и рационально решать квадратные уравнения. Так как в некоторых случаях можно их решать устно, только для этого необходимо помнить алгоритм решения квадратных уравнений, который может пригодиться на экзамене ЕГЭ, при поступлении в ВУЗы и различных жизненных ситуациях.
Квадратное уравнение-это фундамент, на котором покоится величественное здание алгебры.
С помощью формул корней квадратных уравнений можно решить любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения.
Таким образом возникает необходимость изучения этих дополнительных способов решения. Все сказанное выше определяет актуальность темы выполненной работы.
Определение:Квадратным уравнением называется уравнение вида
ax 2 + bx + c =0,
гдех-переменная, а, b и с-некоторые числа, причем,а≠0.
Если в квадратном уравнении ах 2 + bx + c =0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.
Неполные квадратные уравнения бывают трёх видов:
1)ах 2 +с=0, где с ≠ 0;
2) ах 2 + b х = 0, где b ≠ 0;
Квадратные уравнения это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.
1) Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
х 2 + х = , х 2 – х = 14
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
2) Квадратные уравнения в Индии.
ах 2 + b х = с, а> 0
В уравнении коэффициенты, кромеа, могут быть отрицательными. Правило Брахмагупта по существу совпадает с нашим.
3) Квадратные уравнения в Европе XIII - XVII вв.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х 2 + b х = с, при всевозможных комбинациях знаков коэффициентов b , с было сформулировано в Европе лишь в 1544 г. М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
В школьном курсе математике изучают формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно разберем каждые из них.
1) Разложение левой части уравнения на множители .
1. Решим уравнение х 2 + 10х – 24 = 0.
Разложим левую часть уравнения на множители:
х 2 + 10х – 24 = х 2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).
Следовательно, уравнение можно переписать так:
Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = - 12. это означает, что числа 2 и – 12 являются корнями уравнения х 2 + 10х – 24 = 0.
2) Метод выделения полного квадрата
Поясним этот метод на примере.
Решим уравнение х 2 + 6х – 7 = 0
Выделим в левой части полный квадрат. Для этого запишем выражение
х 2 + 6х в следующем виде:
х 2 + 6х = х 2 + 2· х ·3.
В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3. поэтому чтобы получить полный квадрат, нужно прибавить 3 2 , так как
х 2 + 2· х ·3 + 3 2 = (х + 3) 2 .
Преобразуем теперь левую часть уравнения
прибавляя к ней и вычитая 3 2. Имеем:
х 2 + 6х – 7= х 2 + 2· х ·3 + 3 2 – 3 2 – 7= (х + 3) 2 – 9– 7= (х + 3) 2 – 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 –16 = 0, т.е. (х + 3) 2 = 16.
Следовательно, х=3=4,х1=1, или х +3= - 4 , х2 = – 7.
3) Решение квадратных уравнений по формуле
Вывод формулы:
Умножим обе части уравнения
ах 2 + b х + с = 0, а ≠ 0,на 4а и следовательно имеем:
4а 2 х 2 + 4а b с + 4ас = 0.
((2ах) 2 + 2ах · b + b 2 ) – b 2 + 4ас = 0,
(2ах + b ) 2 = b 2 – 4ас,
а) 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 – 4ас = 7 2 – 4· 4 ·3 = 49 – 48 = 1, D >два разных корня;
х = , х = ; х = , х1 = , х = , х2 = –1
Таким образом, в случае положительного дискриминанта,т. е. при b 2 – 4ас≥0 уравнение ах 2 + b х + с = 0 имеет два различных корня.
б) 4х 2 – 4х + 1 = 0,
а =4, b = - 4, с = 1. D = b 2 – 4ас= 16 – 4∙4∙1 = 0, D = 0, один корень;
Итак, если дискриминант равен нулю, т. е. = b 2 – 4ас= 0, тоуравнение ах 2 + b х + с = 0 имеет единственный корень, х =
в) 2х 2 +3х + 4 = 0, а =2, b = 3, с = 4, D = b 2 – 4ас= 9 – 4∙2∙4 =9 – 32 = - 13,
Итак, если дискриминант отрицателен, т. е. = b 2 – 4ас
ах 2 + b х + с = 0 не имеет корней.
4) Решение уравнений с использованием теоремы Виета(прямой и обратной)
а) Как известно, приведенное квадратное уравнение имеет вид
х 2 + px + q = 0. (1)
Его корни удовлетворяют теореме Виета, которая приа = 1 имеет вид
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если свободный член q приведенного уравнения (1) положителен ( q >0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p .
Если p >0, то оба корня отрицательные, если p
х 2 – 3х + 2 = 0; х1 = 2 и х2 = 1, так как q = 2>0 и p = – 3
х 2 +8х + 7 = 0; х1 = – 7 и х2 = – 1, так как q = 7 > 0 и p = 8 >0.
б) Если свободный член q приведенного уравнения (1) отрицателен ( q p p >0.
х 2 + 4х – 5 = 0; х1 = – 5 и х2 = 1, так как q = – 5 p = 4 > 0;
х 2 – 8х – 9 = 0; х1 = 9 и х2 = – 1, так как q = – 9 p = – 8 >0.
б) Теорема Виета для квадратного уравнения
ах 2 +вх+с = 0
Справедлива теорема, обратная теореме Виета:
Если числа х1 и х2 таковы, что х1+х2 = -р, х1х2 = q , то х1 и х2 – корни квадратного уравнения
Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.
1. Решить уравнение: х 2 – 9х + 14 =0
Попробуем найти два числа х1 и х2 , такие, что
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
2. Решить уравнение: х 2 +3х – 28 = 0
Попробуем найти два числа х1 и х2 , такие, что
Нетрудно заметить, что такими числами будут – 7 и 4. Они и являются корнями заданного уравнения.
Рассмотрим квадратное уравнение
ах 2 + b х + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + а b х + ас = 0.
Пусть ах= у, откуда х = ; тогда приходим к уравнению
у 2 + by + ас = 0,
Решим уравнение 2х 2 – 11х + 15 = 0.
у 2 – 11 y +30 = 0.
Согласно теореме Виета
6)Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение
ах 2 + b х + с = 0, а ≠ 0.
1.Если а+ b +с=0 (т.е. сумма коэффициентов уравнения равна нулю),то х1 =1, х2= .Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
Согласно теореме Виета
По условиюа + b + с = 0, откуда b = – а – с. Значит,
Получаем х1=1, х2=, что и требовалось доказать.
2. Если а - b + с = 0, или b = а + с, то х1= – 1, х2 = – .
Доказательство. По теореме Виета
По условию а – b + с = 0, откуда b = а + с. Таким образом,
т.е. х1= – 1 и х2 = , что и требовалось доказать.
1. Решим уравнение 345х 2 –137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то х1=1, х2= = .
Ответ: 1; –.
2. Решим уравнение 132х 2 + 247х + 115 = 0
Решение. Т. к. а- b +с = 0 (132 – 247 +115=0), то
Б. Если второй коэффициент b = 2 k – четное число, то формулу корней
можно записать в виде
Решим уравнение 3х 2 –14х + 16 = 0.
Решение. Имеем: а = 3, b = – 14, c = 16, k = – 7;
D = k 2 – ac = (– 7) 2 – 3 · 16 = 49 – 48 = 1, D >0, два различных корня;
В. Приведенное уравнение
x 2 + px + q = 0
совпадает с уравнением общего вида, в которома = 1, p и c = q . Поэтому для приведенного квадратного уравнения формула корней
Формулу (3) особенно удобно использовать, когда p – четное число.
1. Решим уравнение х 2 –14х – 15 = 0.
Решение. Имеем: х1,2 = 7±= 7±= 7±8.
7)Графическое решение квадратного уравнения
Если в уравнении x 2 + px + q = 0перенести второй и третий члены в правую часть, то получим x 2 = – px – q .
Построим графики зависимостей у = х 2 и у = – px – q . (рис.1)
График первой зависимости – парабола,проходящая через начало координат.График второй зависимости – прямая.Возможны следующие случаи:прямая и парабола могут пересекаться в двух точках, абсциссыточек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут касаться (только одна общая точка),т.е.уравнение имеет одно решение;
- прямая и парабола не имеют общих точек, т.е. квадратноеуравнение не имеет корней.
1. Мордкович А.Г. Алгебра.8 класс. Учебник для общеобразовательных учреждений / А.Г. Мордкович. № 8622 / 0790 – М.: Мнемозина, 2013. № 8622 / 0790 – 260 с.
2. Мордкович А.Г. Алгебра.8 класс. Задачник для общеобразовательных учреждений / А.Г. Мордкович. № 8622 / 0790 – М.: Мнемозина, 2013. № 8622 / 0790 – 270 с.
3. Глейзер Г.И. История математики в № 8622 / 0790 школе / Г.И. Глейзер. № 8622 / 0790 – М.: Просвещение, 1982. № 8622 / 0790 – 340 с.
4. Гусев В.А. Математика. Справочные материалы / В.А. Гусев, А.Г. Мордкович. № 8622 / 0790 – М.: Просвещение, 1988. № 8622 / 0790 – 372 с.
5. Брадис В.М. Четырехзначные математические таблицы для средней школы / В.М. Брадис. № 8622 / 0790 – М.: Просвещение, 1990. № 8622 / 0790 – 83 с.
Теория уравнений занимает ведущее место в алгебре и математике в целом. Значимость ее заключается не только в теоретическом значении для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, что также пригодится и при решении более сложных задач, в том числе и при сдаче экзаменов.
Цель работы: изучить различные способы решения квадратных уравнений, научиться решать квадратные уравнения.
– рассмотреть стандартные и нестандартные методы решения квадратных уравнений;
– выявить наиболее удобные способы решения квадратных уравнений;
– научиться решать квадратные уравнения различными способами.
Объект исследования: квадратные уравнения.
Предмет исследования: способы решения квадратных уравнений.
- теоретические: изучение литературы по теме исследования, изучение тематических Интернет-ресурсов;
- анализ полученной информации;
- сравнение способов решения квадратных уравнений на удобство и рациональность.
Методы решения квадратных уравнений
Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0, где х – переменная, a, b и с – некоторые числа, при этом а ? 0. Корень такого уравнения – это значение переменной, обращающее квадратный трёхчлен в ноль, то есть значение, обращающее квадратное уравнение в тождество. Коэффициенты квадратного уравнения имеют собственные названия: коэффициент а называют первым или старшим, коэффициент b называют вторым или коэффициентом при х, с называется свободным членом этого уравнения.
Полным квадратным уравнением называют такое, все коэффициенты которого отличны от нуля (a, b, c - 0).
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент а: x 2 + px + q = 0, р = b/a, q = c/a.
Неполные квадратные уравнения бывают трёх видов:
1) ax 2 + c = 0, где с - 0;
2) ax 2 + bx = 0, где b - 0;
В рамках данной работы мы будем рассматривать способы решения только полных квадратных уравнений.
Решение квадратных уравнений по общей формуле
Для решения квадратных уравнений применяется способ нахождения корней через дискриминант. Для нахождения дискриминанта используется следующая формула D = b 2 – 4ac. После нахождения D мы используем формулу для нахождения корней уравнения
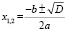
.
Стоит заметить, что если:
D > 0 – уравнение имеет два корня;
D = 0– уравнение имеет один корень;
D 2 + 10x – 24 = 0.
Разложим левую часть на множители:
x 2 + 10x – 24 = x + 12x – 2x – 24 = = x(x + 12) – 2(x + 12) = (x + 12)(x – 2).
Следовательно, уравнение можно переписать так:
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при x = 2, а также при x = –12.
Пример решения уравнения данным способом показан на рис. 1(1.2).
Метод выделения полного квадрата
Выделение полного квадрата – это такое тождественное преобразование, при котором заданный трехчлен представляется в виде (a ± b) 2 суммы или разности квадрата двучлена и некоторого числового или буквенного выражения.
Решим уравнение x 2 + 14x + 40 = 0.
Разложим многочлен на множители методом выделения полного квадрата.
Для применения первой формулы необходимо получить выражение
x 2 + 14x + 49 = 0.
Поэтому прибавим и отнимем от многочлена x 2 + 14x + 40 число 9, чтобы выделить полный квадрат
x 2 + 14x + 40 + 9 – 9 = 0
(x + 14x + 40 + 9) – 9 = 0
(x + 14x + 49) – 9 = 0
(x + 7 – 3)(x + 7 + 3) = 0
x + 4 = 0x + 10 = 0
Пример решения уравнения данным способом показан на рис. 1(1.3).
Решение уравнений с помощью теоремы Виета
Для решения полного квадратного уравнения по теореме Виета нужно разделить всё уравнение на коэффициент а. Для уравнения x 2 + px + q = 0, если х1 и х2 его корни, справедливы формулы:
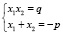
Пример решения уравнения данным способом показан на рис. 1(1.4).
Решение уравнений с использованием свойств коэффициентов
Если выполняется следующее условие: а + с = b, то x1 = – 1; x2 = – с/а.
4x2 + 3x – 1 = 04 – 1 = 3
Если выполняется следующее условие:
а + b + c = 0, то x1 = 1; x2 = с/а.
5x2 + 2x – 7 = 05 + 2 –7 = 0
Пример невозможности решения уравнения данным способом показан на рис. 1(1.5).
Получим: a 2 x2 + abx + aс = 0. Введём новую переменную y = ax. Получим y 2 +by+ac = 0. Корни этого уравнения y1 и y2.Следовательно х1 = y1/a; х2 = y2/a.
Пример решения уравнения данным способом показан на рис. 1(1.6).
Геометрический способ решения квадратных уравнений
Решим уравнение x 2 – 4x – 12 = 0.
Представим его в виде x 2 – 4x = 12.
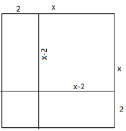
Выполнив замену x 2 – 4x = 12, получим
x – 2 = 4x – 2 = – 4
Ответ: x1 = 6, x1 = – 2.
Пример решения уравнения данным способом показан на рис. 1(1.7).
Графическое решение квадратного уравнения
В уравнении x 2 + px + q = 0 перенесём второй и третий члены в правую часть уравнения. Получим: x 2 = – px – q. Построим графики функций
y = x 2 (парабола);
y = – qx – p (прямая).
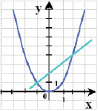
Следует учесть, что:
– если прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
– если прямая касается параболы (только одна общая точка), то уравнение имеет один корень;
– если прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Пример решения уравнения данным способом показан на рис. 1(1.9).
Решение уравнения при помощи циркуля и линейки
Решим уравнение ax 2 + bx + c = 0:
1) построим на координатной плоскости точки:
A(– b/2a; (a + c)/2a) – центр окружности и В(0; 1)
2) Проведём окружность r = AB
3) Абсциссы точек пересечения с осью Ox есть корни исходного уравнения
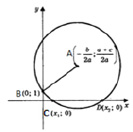
Следует учесть, что:
– если радиус окружности больше ординаты центра (AB > АС, или R > (a + c)/2a), окружность.
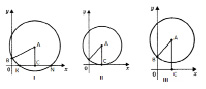
Пересекает ось абсцисс в двух точках К(х1; 0) и N(х2; 0), где х1 и х2 – корни квадратного уравнения x2 + bx + c = 0.
– если радиус окружности равен ординате центра (AB = AС, или R = (a + c)/2a), окружность касается оси абсцисс в точке С(х ; 0), где х1 – корень квадратного уравнения.
– если радиус окружности меньше ординаты центра (AB 2 + pz + q = 0. Если уравнение имеет корни разных знаков, то, найдя по номограмме положительный корень, отрицательный находят, вычитая положительный из – р.
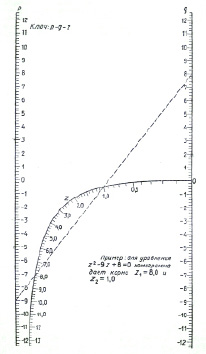
Рис. 6. Вид монограммы для решения уравнения z 2 + pz + q = 0
В случае, когда оба корня отрицательны, берут z = – t и находят по номограмме два положительных корня t1; t 2 уравнения t 2 + – pt + z = 0, а затем z1 = – t1; z 2 = – t2.
Если коэффициенты p и q выходят за пределы шкал, выполняют подстановку z = kt и решают посредством номограммы уравнение
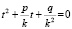
,
где k берётся с таким расчётом, чтобы имели место неравенства
; .
Вид монограммы для решения уравнения z 2 + pz + q = 0 можно найти на рис. 6.
Название способа решения квадратных уравнений
Решение квадратных уравнений по формуле
Можно применить ко всем квадратным уравнениям.
Нужно выучить формулы.
Разложение левой части уравнения на множители
Дает возможность сразу увидеть корни уравнения.
Нужно правильно вычислить слагаемых для группировки.
Метод выделения полного квадрата
За минимальное количество действий можно найти корни уравнений
Нужно правильно найти все слагаемые для выделения полного квадрата.
Решение уравнений с использованием теоремы Виета
Достаточно легкий способ, дает возможность сразу увидеть корни уравнения.
легко находятся только целые корни.
Свойства коэффициентов квадратного уравнения
Не требует особых усилий
Подходит только к некоторым уравнениям
Решение уравнений способом переброски
За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета.
легко найти только целые корни.
Геометрический способ решения квадратных уравнений
похож на способ выделения полного квадрата
Графическое решение квадратного уравнения
Могут быть не точности при составлении графиков
Решение квадратных уравнений с помощью циркуля и линейки
Могут быть не точности
Решение квадратных уравнений с помощью номограммы
Наглядный способ, прост в применении.
Не всегда под рукой имеется номограмма.
В ходе выполнения данной исследовательской работы мне удалось обобщить и систематизировать изученный материал по выбранной теме, изучить различные способы решения квадратных уравнений, научиться решать квадратные уравнения 10 способами. Нужно отметить, что не все они удобны для решения, но каждый из них по-своему интересен. С моей точки зрения, наиболее рациональными для использования будут способы, изучаемые в школе: 1.1. (по формуле); 1.4. (по теореме Виета); а также способ 1.5. (используя свойства коэффициентов).
Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в математике. Эти знания могут пригодиться нам не только в школе и в ВУЗе, но и на протяжении всей жизни.





10 СПОСОБОВ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

Автор работы награжден дипломом победителя II степени
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
1. Методы и способы решения квадратных уравнений 4
1.1. Решение квадратных уравнений по общей формуле. 5
1.2.Разложение левой части на множители. 5
1.3.Метод выделения полного квадрата 5
1.4.Решение уравнений с помощью теоремы Виета 6
1.5.Решение уравнений с использованием свойств коэффициентов. 6
1.7. Геометрический способ решения квадратных уравнений 7
1.8. Графическое решение квадратного уравнения. 7
1.9. Решение уравнения при помощи циркуля и линейки.. 8
1.10.Решение квадратных уравнений с помощью номограммы. 8
Введение
Теория уравнений занимает ведущее место в алгебре и математике в целом. Значимость ее заключается не только в теоретическом значении для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, что также пригодится и при решении более сложных задач, в том числе и при сдаче экзаменов.
Цель работы: изучить различные способы решения квадратных уравнений, научиться решать квадратные уравнения.
Задачи:
- рассмотреть стандартные и нестандартные методы решения квадратных уравнений;
- выявить наиболее удобные способы решения квадратных уравнений;
- научиться решать квадратные уравнения различными способами.
Объект исследования: квадратные уравнения.
Предмет исследования: способы решения квадратных уравнений.
Методы исследования:
теоретические: изучение литературы по теме исследования, изучение тематических Интернет-ресурсов;
анализ полученной информации;
сравнение способов решения квадратных уравнений на удобство и рациональность.
1. Методы решения квадратных уравнений
Квадратным уравнением называется уравнение вида ,где х-переменная, a, b и с-некоторые числа, при этом а≠0. Корень такого уравнения – это значение переменной, обращающее квадратный трёхчлен в ноль, то есть значение, обращающее квадратное уравнение в тождество. Коэффициенты квадратного уравнения имеют собственные названия: коэффициент а называют первым или старшим, коэффициент b называют вторым или коэффициентом при х, с называется свободным членом этого уравнения.
Полным квадратным уравнением называют такое, все коэффициенты которого отличны от нуля (a, b, c≠0).
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент а: , р=b/a, q=c/a.
Неполные квадратные уравнения бывают трёх видов:
В рамках данной работы мы будем рассматривать способы решения только полных квадратных уравнений.
1.1. Решение квадратных уравнений по общей формуле
Для решения квадратных уравнений применяется способ нахождения корней через дискриминант. Для нахождения дискриминанта используется следующая формула . После нахождения D мы используем формулу для нахождения корней уравнения .
Стоит заметить, что если:
D>0 – уравнение имеет два корня;
D=0– уравнение имеет один корень;
), окружность Рис. 4
- если радиус окружности равен ординате центра (AB = AС, или
, окружность касается оси абсцисс в точке С(х1 ; 0), где х1 – корень квадратного уравнения.
Читайте также:

