Замечание к аксиоме 1 кратко
Обновлено: 02.07.2024
Система аксиом I—IX, изложенных в § 1, не является независимой. В настоящем параграфе мы сформулируем систему четырёх аксиом и покажем, что все аксиомы I—IX следуют из этой системы аксиом или содержатся в ней.
Как уже отмечалось выше, мы всегда предполагаем, что все рассматриваемые фигуры расположены в некоторой плоскости, которую мы условились называть основной плоскостью.
Аксиома 1. Основная плоскость построена.
Аксиома 2. Если построены две фигуры, то можно установить является ли их разность пустым множеством или нет.
Аксиома 3. Если разность двух построенных фигур не является пустым множеством, то эта разность также построена.
Следствие 1. Если две фигуры построены, то можно считать известным, является ли их пересечение пустым множеством или нет.
В самом деле, пусть фигуры построены. Обозначим через совокупность тех точек фигуры которые не принадлежат фигуре т. е. пусть Ясно, что можно представить также в виде: так что
Если построены фигуры и то в силу аксиомы 2 известно, является ли разность пустым множеством или нет. Если эта разность — пустое множество, то и мы можем сказать, что пересечение не пусто. Если же не пусто, то в силу аксиомы 3 считается построенной фигура т. е. фигура и в силу аксиомы 2 известно, является ли т. е. пустым множеством или нет. Следствие доказано.
Следствие 2. Если построены две фигуры и их пересечение не пусто, то это пересечение должно считаться построенным.
Это вытекает из аксиомы 3 в силу соотношения:
Следствие 3. Если построены две фигуры, то их соединение должно считаться построенным.
Доказательство. Пусть две построенные фигуры, основная плоскость. Если хотя бы одна из фигур или совпадает с то утверждение верно в силу аксиомы
Пусть отлично от II, а также отлично От силу аксиомы 3 должны считаться построенными фигуры
Воспользуемся теперь следующим тождеством (доказательство этого тождества см., например, в книге П. С. Александрова "Введение в общую теорию множеств и функций", гл. I, § 2, формула 1):
Если множество пусто, то следовательно, фигура должна считаться построенной в силу аксиомы 1. Если же не пусто, то фигура также должна считаться построенной в силу аксиомы 3.
Аксиома 4. Если построены две фигуры, пересечение которых не пусто, то можно построить по крайней мере одну точку, принадлежащую этому пересечению.
Следствие 4. Если построены две фигуры и какое-либо натуральное число, то всегда можно установить, содержит ли пересечение построенных фигур по крайней мере различных точек или оно содержит менее, чем точек.
Для доказательства этого следствия заметим прежде всего, что, согласно следствию 1, можно сказать, является ли пересечение построенных фигур пустым множеством или оно содержит хотя бы одну точку. В первом случае следствие, очевидно, справедливо. Во втором случае, согласно аксиоме 4, можно построить точку принадлежащую пересечению фигур В силу аксиомы 2 при этом будет известно, является ли пустым хотя бы одно из множеств а следовательно, является ли пустым множество Если это множество пусто, то точка является единственной общей точкой фигур Если же не пусто, то в силу аксиомы 4 можно построить хотя бы одну точку принадлежащую как фигуре так и фигуре
Рассмотрим теперь фигуры
Либо их пересечение пусто, и тогда имеют лишь общие точки либо их пересечение не пусто, и тогда можно построить третью общую точку фигур и
Повторяя это рассуждение, после конечного числа шагов мы получим ответ на поставленный вопрос: содержит ли пересечение по крайней мере точек или нет. Следствие доказано.
Следствие 5. Можно построить любое конечное число общих точек двух построенных фигур, если такие точки существуют.
Справедливость этого следствия непосредственно вытекает из хода доказательства следствия 4.
Следствие 6. Можно построить точку, заведомо принадлежащую построенной фигуре.
Доказательство. Пусть построена фигура Будем рассматривать её как пересечение двух фигур: так что В силу аксиомы 4 можно построить точку, принадлежащую пересечению т. е. фигуре
Следствие 7. Можно построить точку на основной плоскости, заведомо не принадлежащую построенной фигуре, если не все точки плоскости принадлежат этой фигуре.
Доказательство. Пусть на основной плоскости построгна некоторая фигура отличная от всей плоскости. Тогда в силу аксиом 1 и 3 должна считаться построенной также фигура В силу следствия 6 можно построить точку, принадлежащую фигуре а значит, заведомо не принадлежащую
Что касается понятия "данная фигура", то ему можно придавать тот же смысл, что и понятию "построенная фигура".
Из-за блокировщика рекламы некоторые функции на сайте могут работать некорректно! Пожалуйста, отключите блокировщик рекламы на этом сайте.

Замечание к аксиоме 1
© DisTTutor LLC 2008 - 2022
- свое имя;
- свою фамилию;
- свой email;
- свой пароль;
- потверждение пароля;
- в качестве кого вы регистрируетесь;
Внимание! Вы собираетесь купить тариф Vip сроком на дней за руб.
Стереометрия - это раздел геометрии, в котором изучаются фигуры в пространстве. В стереометрии, так же как и в планиметрии, свойства геометрических фигур устанавливаются путем доказательства соответствующих теорем. При этом отправными являются свойства основных геометрических фигур, выражаемые аксиомами.
Основными фигурами в пространстве являются точка, прямая и плоскость.
Плоскость мы представляем себе, как ровную поверхность крышки стола и поэтому будем изображать ее в виде параллелограмма.
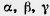
Плоскость, как и прямая, бесконечна. На рисунке мы изображаем только часть плоскости, но представляем ее неограниченно продолженной во все стороны. Плоскости обозначаются греческими буквами
Введение нового геометрического образа — плоскости заставляет расширить систему аксиом. Поэтому мы вводим группу аксиом С, которая выражает основные свойства плоскостей в пространстве. Эта группа состоит из следующих трех аксиом:
С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Сз. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Таким образом, система аксиом стереометрии состоит из аксиом I - IX планиметрии и группы аксиом С.
Замечание. В планиметрии мы имели одну плоскость, на которой располагались все рассматриваемые нами фигуры. В стереометрии много, даже бесконечно много, плоскостей. В связи с этим формулировки некоторых аксиом планиметрии, как аксиом стереометрии, требуют уточнения. Это относится к аксиомам IV, VII, VIII, IX. Приведем эти уточненные формулировки.
IV. Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
VII. От полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
VIII. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
IX. На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Для удобства изложения напомнимаксиому I.
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
Задача 1.Точки А, В, С и D не лежат в одной плоскости. Докажите, что прямые АВ и СD не пересекаются.
Доказательство:
Допустим, что АВ и СД пересекаются, тогда по аксиоме 3 через них можно провести плоскость, и в ней лежат все четыре точки, что противоречит условию задачи. Значит, АВ и СД не пересекаются, что и требовалось доказать.
Задача 2.Можно ли через точку пересечения двух данных прямых провести третью прямую, не лежащую с ними в одной плоскости? Ответ объясните.

Доказательство:
Можно. Пусть прямые aиbпересекаются в точке С и лежат в плоскости α (аксиома 3, рис.1). Тогда возьмем точку D вне плоскости α (по аксиоме 1) и рассмотрим прямую CD. Это прямая не принадлежит плоскости α, а плоскость, содержащая прямые a и b,единственная (аксиома 3). Значит, прямая CD удовлетворяет условию задачи.
Задачи
Цель. Учиться анализировать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения.

1. Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.
2. Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из данных плоскостей, пересекает и другую.
3. Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.
4. Даны четыре точки, не лежащие в одной плоскости. Сколько можно провести различных плоскостей, проходящих через три из этих точек? Объясните ответ.
5. Можно ли через три точки, лежащие на одной прямой, провести две различные плоскости? Объясните ответ.
Стереометрия - это раздел геометрии, в котором изучаются фигуры в пространстве. В стереометрии, так же как и в планиметрии, свойства геометрических фигур устанавливаются путем доказательства соответствующих теорем. При этом отправными являются свойства основных геометрических фигур, выражаемые аксиомами.

Основными фигурами в пространстве являются точка, прямая и плоскость.
Плоскость мы представляем себе, как ровную поверхность крышки стола и поэтому будем изображать ее в виде параллелограмма.
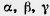
Плоскость, как и прямая, бесконечна. На рисунке мы изображаем только часть плоскости, но представляем ее неограниченно продолженной во все стороны. Плоскости обозначаются греческими буквами
Введение нового геометрического образа — плоскости заставляет расширить систему аксиом. Поэтому мы вводим группу аксиом С, которая выражает основные свойства плоскостей в пространстве. Эта группа состоит из следующих трех аксиом:
С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Сз. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Таким образом, система аксиом стереометрии состоит из аксиом I - IX планиметрии и группы аксиом С.
Замечание. В планиметрии мы имели одну плоскость, на которой располагались все рассматриваемые нами фигуры. В стереометрии много, даже бесконечно много, плоскостей. В связи с этим формулировки некоторых аксиом планиметрии, как аксиом стереометрии, требуют уточнения. Это относится к аксиомам IV, VII, VIII, IX. Приведем эти уточненные формулировки.
IV. Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
VII. От полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
VIII. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
IX. На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Для удобства изложения напомнимаксиому I.
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
Задача 1.Точки А, В, С и D не лежат в одной плоскости. Докажите, что прямые АВ и СD не пересекаются.
Доказательство:
Допустим, что АВ и СД пересекаются, тогда по аксиоме 3 через них можно провести плоскость, и в ней лежат все четыре точки, что противоречит условию задачи. Значит, АВ и СД не пересекаются, что и требовалось доказать.
Задача 2.Можно ли через точку пересечения двух данных прямых провести третью прямую, не лежащую с ними в одной плоскости? Ответ объясните.

Доказательство:
Можно. Пусть прямые aиbпересекаются в точке С и лежат в плоскости α (аксиома 3, рис.1). Тогда возьмем точку D вне плоскости α (по аксиоме 1) и рассмотрим прямую CD. Это прямая не принадлежит плоскости α, а плоскость, содержащая прямые a и b,единственная (аксиома 3). Значит, прямая CD удовлетворяет условию задачи.
Задачи
Цель. Учиться анализировать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения.

1. Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.
2. Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из данных плоскостей, пересекает и другую.
3. Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.
4. Даны четыре точки, не лежащие в одной плоскости. Сколько можно провести различных плоскостей, проходящих через три из этих точек? Объясните ответ.
5. Можно ли через три точки, лежащие на одной прямой, провести две различные плоскости? Объясните ответ.

Чтобы щелкать задачки по геометрии, важно рассуждать логически. Это качество поможет быстрее запомнить все правила и перейти к решению задач и доказательствам. В этой статье узнаем про аксиомы, теоремы и доказательства теорем.
О чем эта статья:
Понятие аксиомы
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
- Через любые две точки проходит единственная прямая.
- Каждая точка на прямой разбивает эту прямую на две части так, что точки из разных частей лежат по разные стороны от данной точки. А точки из одной части лежат по одну сторону от данной точки.
- На любом луче от его начала можно отложить только один отрезок, равный данному.
- Отрезки, полученные сложением или вычитанием соответственно равных отрезков — равны.
- Каждая прямая на плоскости разбивает эту плоскость на две полуплоскости. При этом если две точки принадлежат разным частям, то отрезок, который соединяет эти две точки, пересекается с прямой. Если две точки принадлежат одной части, то отрезок, соединяющий эти точки, не пересекается с прямой.
- От любого луча на плоскости в заданную сторону можно отложить только один угол, который равен данному. Все развернутые углы равны.
- Углы равны, если они получились путем сложения или вычитания соответственно равных углов.
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.

У этой аксиомы два следствия:
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:

Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
- если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
- если две прямые параллельны третьей прямой, то они параллельны.
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
- Синтетический или синтез — метод, при котором данное предложение выступает, как необходимое следствие другого, уже доказанного.
- Аналитический или анализ — обратный синтезу способ. Рассуждения всегда начинаются с доказываемой теоремы и закачиваются другой известной истиной.
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
- Способ наложения — когда одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений в зависимости от того, совмещаются они или нет при наложении.
- Способ пропорциональности — применение свойств пропорций. Этот способ пригодится для доказательства теорем про подобные фигуры и пропорциональные отрезки.
- Способ пределов — когда вместо данной величины берут свойства другой, близкой к ней. А потом перекладывают эти выводы на исходные данные.
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
- прямая теорема: в треугольнике против равных сторон лежат равные углы.
- обратная теорема: в треугольнике против равных углов лежат равные стороны.
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
- Прямая: если при пересечении двух прямых третьей соответственные углы равны, то данные прямые параллельны.
- Обратная: если две прямые параллельны, то при пересечении их третьей, соответственные углы равны.
- Противоположная: если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
- Обратная противоположной: если прямые не параллельны, соответственные углы не равны.
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:

Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:

где a, b и c — стороны плоского треугольника,
α — угол, противолежащий стороне а.

Следствия из теоремы косинусов:
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.

Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:

Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Читайте также:

