Взаимное расположение пространственных фигур кратко
Обновлено: 05.07.2024
Среди пространственных фигур выделяют многогранники – тела, поверхности которых состоят из конечного числа многоугольников, называемых гранями многогранника. Стороны этих многоугольников называют ребрами, вершины – вершинами многогранника.
Диагонали многогранника- отрезки, соединяющие вершины , не принадлежащие одной грани.
Примеры многогранников : (пространственные фигуры)
КУБ- многогранник, поверхность которого состоит из 6ти квадратов.
ПАРАЛЛЕЛЕПИПЕД- многогранник, поверхность которого состоит из 6ти параллелограммов. Параллелепипед, у которого все грани- прямоугольники, называется прямоугольным.
ПРИЗМА- многогранник, поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы, и параллелограммов, имеющих общие стороны с каждым из оснований (боковые грани призмы). Ребра, не лежащие в основаниях призмы, называются боковыми ребрами. Призма, боковыми гранями которой являются прямоугольники, называется прямой. В противном случае призма называется наклонной. Призмы бывают треугольные, четырехугольные, пятиугольные и т.д. в зависимости от того, какие многоугольники лежат в их основаниях : треугольники, четырехугольники, пятиугольники и т.д..
ПИРАМИДА- многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников, имеющих общую вершину – боковые грани пирамиды. Общая их вершина называется вершиной пирамиды. Ребра, сходящиеся в вершине пирамиды, называются боковыми ребрами. Пирамида, в основании которой лежит правильный многоугольник и все боковые ребра которой равны, называется правильной. Пирамиды бывают треугольные, четырехугольные, пятиугольные и т.д. в зависимости от того, какие многоугольники лежат в их основаниях : треугольники, четырехугольники, пятиугольники и т.д.. Треугольная пирамида называется также тетраэдром.
Пространственные фигуры, не являющиеся многогранниками:
СФЕРА- фигура, состоящая из всех точек пространства, удаленных от данной точки, называемой центром, на данное расстояние, называемое радиусом.
ШАР- фигура, состоящая из всех точек пространства, удаленных от данной точки, называемой центром, на расстояние, не превосходящее данное, называемое радиусом.
Сфера с тем же центром и того же радиуса, что и данный шар, называется поверхностью шара.
Также примерами пространственных фигур является цилиндр и конус.
P.S.Я лично буду учить ТОЛЬКО про сами фигуры, но на стр. 312( пар. 35) написано еще что такое подобие, движение в пространстве. Захотите-посмотрите.
6. Параллельность прямых в пространстве
ОПРЕДЕЛЕНИЕ: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
ТЕОРЕМА: Через точку в пространстве, не принадлежащую данной прямой, проходит единственная прямая, параллельная данной прямой.
Док-во- Пусть точка А не принадлежит прямой b. Проведем через эту прямую и точку А плоскость альфа. Эта плоскость единственна. В плоскости через точку А проходит единственная прямая, назовем ее а, параллельная прямой b. Она и будет искомой прямой, параллельной данной.
Прямые в пространстве могут не пересекаться, но и не быть параллельными.
ОПРЕДЕЛЕНИЕ: Две прямые в пространстве называются скрещивающимися, если через них нельзя провести плоскость.
Также два отрезка скрещиваются, если они лежат на скрещивающихся прямых.
Лежат в одной плоскости Не лежат в одной плоскости
1)имеют общую точку(пересекаются) Не лежат в одной плоскости (скрещиваются)
2)не имеют общих точек(параллельны)
ПРИМЕР 1: Через каждые две параллельные прямые можно провести плоскость. Таким образом, если имеются три параллельные прямые, не лежащие в одной плоскости, то через них можно провести три плоскости, если 4 прямые, то 6 плоскостей, если n прямых, то через каждую можно провести n-1 плоскость. Учитывая, что при общем подсчете каждая плоскость будет считаться дважды, получаем общее число плоскостей: n(n-1)/2.
ПРИМЕР 2(признак скрещивающихся прямых):
Если одна прямая лежит в одной плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти две прямые скрещивающиеся.

Пусть прямая а лежит в плоскости альфа, а прямая b пересекает плоскость альфа в точке В, не принадлежащей прямой а.
Если бы прямые а и b лежали в одной плоскости, то в этой плоскости лежали бы прямая а и точка В. Поскольку через прямую и точку вне этой прямой проходит единственная плоскость, то этой плоскостью будет плоскость альфа. Но тогда прямая b лежала бы в плоскости альфа, что противоречит условию. Следовательно, а и b не лежат в этой плоскости, то есть они скрещиваются.
7. Параллельность прямой и плоскости.
ОПРЕДЕЛЕНИЕ: Прямая называется параллельной плоскости, если она не имеет с ней ни одной общей точки.
Прямая и плоскость
Имеют общие точки Не имеют общих точек(параллельны)
1)Имеют одну общую точку(пересекаются)
2)Имеют более одной общей точки(прямая лежит в плоскости)
ТЕОРЕМА(ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ): Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия их пересечения параллельна данной прямой.
Док-во: Пусть плоскость альфа проходит через прямую а, параллельную плоскости бэтта, и прямая b является линией пересечения этих плоскостей. Докажем, что прямые а и b параллельны.
Действительно они лежат в одной плоскости альфа. Кроме этого, прямая b лежит в плоскости бэтта, а прямая а не пересекается с этой плоскостью. Следовательно, прямая а и подавно не пересекается с прямой b. Таким образом, прямые а и b лежат в одной плоскости и не пересекаются. Значит, они параллельны.
ТЕОРЕМА(ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ): Если прямая, не ежащая в данной плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то эта прямая параллельна самой плоскости.
Док-во: Пусть прямая а не лежит в плоскости бэтта и параллельна прямой b, лежащей в этой плоскости. Докажем, что прямая а параллельна плоскости бэтта. Предположим противное, т.е. что прямая а пересекает плоскость бэтта в некоторой точке С. Рассмотрим плоскость альфа, проходящую чеоез прямые а и b (они параллельны по условию) . Точка С принадлежит и плоскости бэтта, и плоскости альфа, т.е. принадлежит линии их пересечение, т.е. прямой b. Следовательно, прямые а и b пересекаются, а это противоречит условию. Таким образом, прямая а параллельна плоскости бэтта.
P.S. Параграф 37, страница 326- также пример
8.Параллельность двух плоскостей
ОПРЕДЕЛЕНИЕ: Две плоскости называются параллельными, если не имеют общих точек.
Имеют общие точки(перес. По прямой) Не имеют общих точек(параллельны)
ТЕОРЕМА: Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Док-во: Пусть плоскость гамма пересекает параллельные плоскости альфа и бэтта по прямым а и b соответственно.
Прямые лежат в одной плоскости-плоскости гамма. Кроме этого, они лежат в непересекающихся плоскостях, следовательно, и подавно не пересекаются. Значит, они параллельны.
ТЕОРЕМА(ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПЛОСКОСТЕЙ): Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Док-во: Пусть пересекающиеся прямые а1, а2 плоскости альфа соответственно параллельны прямым b1, b2 плоскости бэтта. Покажем, что эти плоскости параллельны. Предположим обратное, т.е. что плоскости альфа и бэтта пересекаются и пусть с-линия их пересечения. По признаку параллельности прямой и плоскости прямая а1 параллельна плоскости бэтта, а по свойству параллельности прямой и плоскости она параллельна прямой с. Аналогично прямая а2 параллельна прямой с. Таким образом, в плоскости альфа мы имеем две пересекающиеся прямые, параллельные одной прямой, а это невозможно. Полученное показывает, что неверным было первоначальное предположение о том, что плоскости альфа и бэтта пересекаются, и, следовательно, они параллельны.
P.S. Параграф 38, страница 330-там есть 3 примера – док-во, что основания призмы параллельны и т.п.. Я не знаю нужно это или нет, но если что смотрите, страницы я указала.
5. Пространственные фигуры
Среди пространственных фигур выделяют многогранники – тела, поверхности которых состоят из конечного числа многоугольников, называемых гранями многогранника. Стороны этих многоугольников называют ребрами, вершины – вершинами многогранника.
Диагонали многогранника- отрезки, соединяющие вершины , не принадлежащие одной грани.
Примеры многогранников : (пространственные фигуры)
КУБ- многогранник, поверхность которого состоит из 6ти квадратов.
ПАРАЛЛЕЛЕПИПЕД- многогранник, поверхность которого состоит из 6ти параллелограммов. Параллелепипед, у которого все грани- прямоугольники, называется прямоугольным.
ПРИЗМА- многогранник, поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы, и параллелограммов, имеющих общие стороны с каждым из оснований (боковые грани призмы). Ребра, не лежащие в основаниях призмы, называются боковыми ребрами. Призма, боковыми гранями которой являются прямоугольники, называется прямой. В противном случае призма называется наклонной. Призмы бывают треугольные, четырехугольные, пятиугольные и т.д. в зависимости от того, какие многоугольники лежат в их основаниях : треугольники, четырехугольники, пятиугольники и т.д..
ПИРАМИДА- многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников, имеющих общую вершину – боковые грани пирамиды. Общая их вершина называется вершиной пирамиды. Ребра, сходящиеся в вершине пирамиды, называются боковыми ребрами. Пирамида, в основании которой лежит правильный многоугольник и все боковые ребра которой равны, называется правильной. Пирамиды бывают треугольные, четырехугольные, пятиугольные и т.д. в зависимости от того, какие многоугольники лежат в их основаниях : треугольники, четырехугольники, пятиугольники и т.д.. Треугольная пирамида называется также тетраэдром.
Пространственные фигуры, не являющиеся многогранниками:
СФЕРА- фигура, состоящая из всех точек пространства, удаленных от данной точки, называемой центром, на данное расстояние, называемое радиусом.
ШАР- фигура, состоящая из всех точек пространства, удаленных от данной точки, называемой центром, на расстояние, не превосходящее данное, называемое радиусом.
Сфера с тем же центром и того же радиуса, что и данный шар, называется поверхностью шара.
Также примерами пространственных фигур является цилиндр и конус.
P.S.Я лично буду учить ТОЛЬКО про сами фигуры, но на стр. 312( пар. 35) написано еще что такое подобие, движение в пространстве. Захотите-посмотрите.
6. Параллельность прямых в пространстве
ОПРЕДЕЛЕНИЕ: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
ТЕОРЕМА: Через точку в пространстве, не принадлежащую данной прямой, проходит единственная прямая, параллельная данной прямой.
Док-во- Пусть точка А не принадлежит прямой b. Проведем через эту прямую и точку А плоскость альфа. Эта плоскость единственна. В плоскости через точку А проходит единственная прямая, назовем ее а, параллельная прямой b. Она и будет искомой прямой, параллельной данной.
Прямые в пространстве могут не пересекаться, но и не быть параллельными.
ОПРЕДЕЛЕНИЕ: Две прямые в пространстве называются скрещивающимися, если через них нельзя провести плоскость.
Также два отрезка скрещиваются, если они лежат на скрещивающихся прямых.
Лежат в одной плоскости Не лежат в одной плоскости
1)имеют общую точку(пересекаются) Не лежат в одной плоскости (скрещиваются)
2)не имеют общих точек(параллельны)
ПРИМЕР 1: Через каждые две параллельные прямые можно провести плоскость. Таким образом, если имеются три параллельные прямые, не лежащие в одной плоскости, то через них можно провести три плоскости, если 4 прямые, то 6 плоскостей, если n прямых, то через каждую можно провести n-1 плоскость. Учитывая, что при общем подсчете каждая плоскость будет считаться дважды, получаем общее число плоскостей: n(n-1)/2.
ПРИМЕР 2(признак скрещивающихся прямых):
Если одна прямая лежит в одной плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти две прямые скрещивающиеся.
Пусть прямая а лежит в плоскости альфа, а прямая b пересекает плоскость альфа в точке В, не принадлежащей прямой а.
Если бы прямые а и b лежали в одной плоскости, то в этой плоскости лежали бы прямая а и точка В. Поскольку через прямую и точку вне этой прямой проходит единственная плоскость, то этой плоскостью будет плоскость альфа. Но тогда прямая b лежала бы в плоскости альфа, что противоречит условию. Следовательно, а и b не лежат в этой плоскости, то есть они скрещиваются.
7. Параллельность прямой и плоскости.
ОПРЕДЕЛЕНИЕ: Прямая называется параллельной плоскости, если она не имеет с ней ни одной общей точки.
Прямая и плоскость
Имеют общие точки Не имеют общих точек(параллельны)
1)Имеют одну общую точку(пересекаются)
2)Имеют более одной общей точки(прямая лежит в плоскости)
ТЕОРЕМА(ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ): Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия их пересечения параллельна данной прямой.
Док-во: Пусть плоскость альфа проходит через прямую а, параллельную плоскости бэтта, и прямая b является линией пересечения этих плоскостей. Докажем, что прямые а и b параллельны.
Действительно они лежат в одной плоскости альфа. Кроме этого, прямая b лежит в плоскости бэтта, а прямая а не пересекается с этой плоскостью. Следовательно, прямая а и подавно не пересекается с прямой b. Таким образом, прямые а и b лежат в одной плоскости и не пересекаются. Значит, они параллельны.
ТЕОРЕМА(ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ): Если прямая, не ежащая в данной плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то эта прямая параллельна самой плоскости.
Док-во: Пусть прямая а не лежит в плоскости бэтта и параллельна прямой b, лежащей в этой плоскости. Докажем, что прямая а параллельна плоскости бэтта. Предположим противное, т.е. что прямая а пересекает плоскость бэтта в некоторой точке С. Рассмотрим плоскость альфа, проходящую чеоез прямые а и b (они параллельны по условию) . Точка С принадлежит и плоскости бэтта, и плоскости альфа, т.е. принадлежит линии их пересечение, т.е. прямой b. Следовательно, прямые а и b пересекаются, а это противоречит условию. Таким образом, прямая а параллельна плоскости бэтта.
P.S. Параграф 37, страница 326- также пример
8.Параллельность двух плоскостей
ОПРЕДЕЛЕНИЕ: Две плоскости называются параллельными, если не имеют общих точек.
Имеют общие точки(перес. По прямой) Не имеют общих точек(параллельны)
ТЕОРЕМА: Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Док-во: Пусть плоскость гамма пересекает параллельные плоскости альфа и бэтта по прямым а и b соответственно.
Прямые лежат в одной плоскости-плоскости гамма. Кроме этого, они лежат в непересекающихся плоскостях, следовательно, и подавно не пересекаются. Значит, они параллельны.
ТЕОРЕМА(ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПЛОСКОСТЕЙ): Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Док-во: Пусть пересекающиеся прямые а1, а2 плоскости альфа соответственно параллельны прямым b1, b2 плоскости бэтта. Покажем, что эти плоскости параллельны. Предположим обратное, т.е. что плоскости альфа и бэтта пересекаются и пусть с-линия их пересечения. По признаку параллельности прямой и плоскости прямая а1 параллельна плоскости бэтта, а по свойству параллельности прямой и плоскости она параллельна прямой с. Аналогично прямая а2 параллельна прямой с. Таким образом, в плоскости альфа мы имеем две пересекающиеся прямые, параллельные одной прямой, а это невозможно. Полученное показывает, что неверным было первоначальное предположение о том, что плоскости альфа и бэтта пересекаются, и, следовательно, они параллельны.
Пирамида – это многогранник, одна грань которого (основание) произвольный многоугольник, а остальные грани (боковые стороны) – треугольники с общей вершиной. Так, в основании египетских пирамид лежат прямоугольники…, представили? Отлично!
Пирамида с основанием-треугольником называется треугольной пирамидой или тетраэдром. На рисунке слева точка является вершиной, а – основанием пирамиды.
Объём пирамиды (любой) можно вычислить по формуле , где – площадь основания, – длина проведённой к нему высоты, для нашего тетраэдра: .
Сфера – это множество точек пространства, равноудалённых от заданной точки :
Точка называется центром сферы, а значение – радиусом. Площадь поверхности сферы равна: .
Тело, ограниченное сферой (+ сама сфера), называется шаром. Не путайте эти понятия! Сфера – поверхность, шар – тело.
Объём шара (!) можно вычислить по формуле .
Следующие тела и поверхности я приведу в описательном порядке (без строгих определений). Всем знакомый прямой круговой цилиндр:
Данное тело ограничено равными параллельными кругами сверху и снизу (основания цилиндра), а боковая поверхность порождена образующими (в частности, ) – перпендикулярами, которые соединяют окружности. Площадь боковой поверхности: , где – высота цилиндра, а – радиус основания. Чтобы найти площадь поверхности всего цилиндра нужно приплюсовать площадь двух кругов: . Объём цилиндра: .
Существует великое множество других цилиндров, но во избежание путаницы мы ограничимся лишь этим частным случаем, рАвно, как и одним частными случаем конуса:
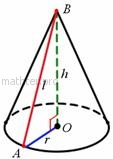
Прямой круговой конус – это тело, ограниченное кругом (основание конуса) и образующими – отрезками равной длины , которые соединяют окружность с вершиной конуса , которая расположена строго над (или под) центром круга:
Если известен радиус основания и высота конуса , то длину образующей можно найти с помощью теоремы Пифагора по формуле . Площадь боковой поверхности конуса равна: , а чтобы вычислить площадь поверхности всего конуса нужно добавить площадь круга: .
И объём конуса: . Есть ещё усечённый конус, но…
Информации этой главы должно хватить в 90-95% случаев! Ну а для случаев других есть учебники / справочники, где можно отыскать более редкие фигуры и формулы.
…никогда не думал, что прикладную геометрию можно изложить на 9,5 страницах… :)
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Новозыбковского района, Брянской области
243015 Брянская область Новозыбковский район с.Верещаки ул. Коммунистическая д.42
Региональная научная конференция
Пугачёва Валерия, Прядко Ростислав, учащиеся 5 кл.
Руководитель :
учитель математики Шинкоренко М. П.
В работе рассматриваются фигуры, изучаемые в геометрии, происхождения их названий, изображение на плоскости. Найдены ответы на вопросы: какие геометрические фигуры встречаются в предметах и объектах, которые нас окружают? Можно ли развёрнуть геометрические тела? Как геометрические фигуры превратить в ёлочные игрушки?
В результате работы созданы модели новогодних игрушек из моделей геометрических тел.
Семейство геометрических фигур
Откуда пришли названия геометрических фигур? ------------------- 8
Изображение пространственных фигур на плоскости ---------------- 8
Можно ли развернуть геометрические тела? --------------------------- 10
Как геометрические фигуры превратить в ёлочные игрушки ------ 11
Всё вокруг – геометрия
Ле Корбюзье
Посмотрите вокруг себя, выгляните в окно, или лучше, пройдитесь по улице, а потом полистайте книги, журналы, альбомы и вы увидите самые разные предметы и объекты. Если не говорить ни о том, из чего они сделаны, ни о том, какого они цвета, ни о том, кто дал им имена, кто придумал и изготовил их, несмотря на такие ограничения, в каждом предмете останется то, что объединяет его со всеми другими предметами и объектами. Это – форма! Например, ствол дерева, стакан, башня … имеют одинаковую форму.
Была выдвинута гипотеза : в повседневной жизни есть место геометрии.
Цель : познакомиться с геометрическими телами
Что такое геометрическая фигура?
Какие фигуры изучает геометрия?
Откуда произошли названия геометрических фигур?
Как изображают пространственные фигуры на плоскости?
Выяснить, какие геометрические фигуры встречаются в предметах и объектах, которые нас окружают?
Можно ли развёрнуть геометрические тела?
Как геометрические фигуры превратить в ёлочные игрушки?
Выполнить презентацию и создать модели новогодних игрушек из моделей геометрических тел.
Личный вклад авторов : весь класс принимали участие в изготовлении моделей геометрических тел.
Новизна: превращение геометрических тел в новогодние игрушки.
Основная часть
Геометрия изучает форму и взаимное расположение фигур в пространстве. Это то пространство, которое нас окружает. Мы живём в мире трёх измерений. Все предметы (тела) в окружающем нас мире имеют длину, ширину, высоту, хотя далеко не у всех можно указать эти измерения.
Семейство геометрических фигур.
Многогранники ( пирамиды и призмы) - т ела, поверхность которых состоит из многоугольников.
Призмы бывают разные: треугольные, четырёхугольные… При всём различии они имеют ряд общих свойств. Например, поверхность каждой призмы состоит из плоских многоугольников, которые называют гранями. Два соседних плоских многоугольника имеют общую сторону – ребро. Концы рёбер являются вершинами призмы. Каждая призма имеет два основания, грани, рёбра.
Куб – является самым ярким представителем призм
Прямоугольный параллелепипед можно считать символом нашего пространства. Это геометрическое тело полностью описывается тремя измерениями – длиной, шириной, высотой.
Пирамиды . Если к стороне одного правильного треугольника, лежащего на столе, приставить ещё три таких треугольника так, чтобы одна вершина оказалась общей, то получится объёмное геометрическое тело – пирамида .
Тела вращения ( цилиндры, конусы, шары)
Цилиндр - геометрическое тело, образуемое вращением прямоугольника около одной из его сторон. Его поверхность состоит из двух одинаковых оснований и боковой поверхности. Основания цилиндра – круги, а боковая поверхность – прямоугольник.
Конус - геометрическое тело, образуемое вращением прямоугольного треугольника около одного из катетов. Его поверхность состоит из основания (кру г) и боковой поверхности (прямоугольнок). Конус имеет вершину.
Шар. Все точки пространства, удалённые от данной точки (центра) на одно и тоже расстояние, образуют сферу. Часть пространства, состоящую из всех точек сферы и всех точек, находящихся внутри сферы, называют шаром. То есть шар – геометрическое тело, его поверхность называют сферой. Шар получается вращением полукруга около диаметра.
Откуда пришли названия геометрических фигур?
Почти все названия геометрических фигур греческого происхождения, как и само слово, геометрия , происходящее от греческого слова γεωμετρία (геометрия) – землемерие. Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский.
Слово призма латинская форма πρισμα (призма) – опиленная (имелось в виду опиленное дерево
Слово цилиндр происходит от латинского слова cylindrus (цилиндрус), являющегося латинской формой греческого слова χύλινδρος (кюлиндрос), означающего валик, каток .
Словом пирамида – πυραμιζ – греки называли сооружения, которые воздвигали египтяне в память о своих фараонах.
Слово шар латинская форма греческого слова σφατρα (сфайра) – мяч, а слово конус – от греческого слова ξωνοσ, что означает шишка .
Изображение пространственных фигур на плоскости.
В геометрии для облегчения восприятия пространства договорились изображать линии, скрытые от взора наблюдателя, пунктирными.
Можно ли развернуть геометрические тела?
Конфету можно развернуть, покупки всякие … А геометрические фигуры? Если их разрезать по рёбрам, а затем развернуть, то получатся развёртки призм, пирамид, цилиндров, конусов.
Поверхность призмы состоит из двух оснований и боковых граней. Каждая боковая грань призмы – прямоугольник, основание – равные многоугольники. Следовательно, развёртка поверхности призмы содержит прямоугольники и два равных многоугольника.
Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник, основание – многоугольник. Следовательно, развёртка поверхности пирамиды содержит треугольники и один многоугольник.
Развёртка поверхности цилиндра : два круга и плоский прямоугольник.
Развёртка поверхности конуса : круг и часть круга.
Только шар не разворачивается . Нет у шара развёртки!
Геометрические фигуры вокруг нас
Призмы. Оглянитесь вокруг себя, и вы всюду обнаружите призмы. Такую форму имеют дом, книга, шкаф …

Цилиндры. В жизни цилиндр – это башня, кактус, колбаса, резиновый шланг, труба на доме, железные прутья в ограде сквера …

Конусы. Шишки, шляпки грибов, ель могут служить примером тел имеющих форму конуса.

Шары. Представление о шаре нам даёт арбуз, апельсин, яблоко.
Дача в Подмосковье
Как геометрические фигуры превратить в ёлочные игрушки?
Теперь мы знаем, как выглядят развёртки поверхностей геометрических тел – цилиндра, конуса, пирамиды, призмы. Используя их, мы постарались смастерить всякие забавные новогодние игрушки.






Познакомились с разными видами многогранников и тел вращения.
Узнали, что названия геометрических тел греческого происхождения.
Научились изображать и изготавливать их.
Подготовили презентацию и изготовили новогодние игрушки из геометрических тел.
Выяснили, что мир, в котором мы живём, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека.
Среди человеческих творений самым волшебным являются новогодние игрушки.
В. А. Панчищина, Э. Г. Гельфман и др. Геометрия 1 часть: изд. Томского университета, Томск, 1998 г.
С пространственными геометрическими фигурами (куб, шар, параллелепипед и др.) дети знакомятся в практической деятельности (при конструировании, во время игры) гораздо раньше, чем с плоскими фигурами. Особенности мышления младших дошкольников определяют выбор наглядного материала. В этом возрасте важно, чтобы изучаемый объект был крупный, яркий, чтобы им можно было выполнять действия (поиграть). Обследование идет на сенсорной основе, поэтому с моделями объемных фигур детям знакомиться легче. Кубики, шарики, бруски и др. входят в игру детей одновременно с первыми игрушками. Обычно математические названия им не даются, но идет знакомство с различными объемными формами, а в речь вводятся только некоторые термины.
Основными фигурами в пространстве считаются: точка, прямая, плоскость. На каждой плоскости выполняются все утверждения планиметрии. В стереометрии, так же как в планиметрии, вводится ряд аксиом, которые изучаются в школьном курсе геометрии.
Объемные геометрические фигуры называют геометрическими телами. В пространстве выделяют многогранники (призма, пирамида и др.) и тела вращения (шар, конус, цилиндр и др.).
Многогранники
Многогранник – это ограниченное тело, поверхность которого состоит из конечного числа многоугольников. Эти многоугольники называются гранями, их стороны – ребрами, а вершины – вершинами многогранника.
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости любой его грани (рис. 70).
Выпуклый многогранник невыпуклый многогранник
Задание 43
Покажите вершины, ребра и грани многогранников, изображенных на рисунке 70. Какими геометрическими фигурами они являются?
Правильный выпуклый многогранник имеет грани – правильные равные многоугольники, и в каждой его вершине сходится одинаковое число ребер.
Задание 44
1. Вспомните, какие фигуры называют равными.
2. Назовите известные вам правильные выпуклые многогранники.
Всего существует 5 правильных многогранников, в отличие от правильных многоугольников, которых бесконечно много. Это обусловлено двумя причинами:
1. Сумма плоских углов, сходящихся в одной вершине, должна быть меньше 360º.
2. Сумма ребер, сходящихся в одной вершине должна быть не меньше 3.

Задание 45
Дайте определение каждому из правильных выпуклых многогранников.
Одним из самых знакомых детям правильных многогранников является куб (гексаэдр).
Куб – это правильный многогранник, гранями которого являются равные квадраты, а в каждой вершине сходятся по 3 ребра.
Среди выпуклых многогранников выделяют призмы и пирамиды.
Детские конструкторы содержат различные виды призм (рис. 72), а также другие многогранники.
треугольная прямоугольный куб шестиугольная
призма параллелепипед призма
Призма – это многогранник, состоящий из двух плоских многоугольников (оснований), лежащих в разных плоскостях, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (рис. 73).
В зависимости от количества углов многоугольника, являющегося основанием, призмы бывают: треугольные (рис. 74), четырехугольные и другие.
Задание 46
1. Вспомните, что такое параллельный перенос.
2. Нарисуйте четырехугольную призму. Покажите ее основания, боковую поверхность, боковые грани и ребра. Какими геометрическими фигурами они являются?
Частным случаем призмы являются прямоугольный параллелепипед и куб. Модели этих фигур используются маленькими детьми в строительных играх.
Прямоугольный параллелепипед – это параллелепипед, все грани которого прямоугольники (рис. 75).
Куб – это прямоугольный параллелепипед с равными ребрами (или все грани которого являются квадратами) (рис. 76).
Пирамида – многогранник, состоящий из плоского многоугольника (основания), точки, не лежащей в плоскости основания (вершины), и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 77). Отрезки, соединяющие вершины пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Все боковые грани – треугольники.
В зависимости от числа углов многоугольника, являющегося основанием, пирамиды бывают: треугольные (рис. 77а), четырехугольные (рис. 77б), пятиугольные и другие пирамиды.
Любая грань треугольной пирамиды может служить ее основанием. Это же название носит и правильный многогранник, тетраэдр, гранями которого являются равные равносторонние треугольники.
Задание 47
1. Нарисуйте пятиугольную пирамиду. Покажите ее основание, боковую поверхность, боковые грани и ребра. Какими геометрическими фигурами они являются?
2. Дайте определение высоты пирамиды и правильной пирамиды.
Тела вращения
Изучая форму окружающих предметов, дошкольники сталкиваются с телами вращения (рис. 78).
цилиндр конус шар
Эти фигуры называются телами вращения, так как они могут быть получены путем вращения некоторых плоских геометрических фигур.
Цилиндр – это тело вращения, которое может быть получено путем вращения прямоугольника вокруг одной из его сторон, как оси (рис. 79).
Конус – это тело вращения, которое может быть получено путем вращения прямоугольного треугольника вокруг одного из его катетов, как оси (рис. 80).
Шар – это тело вращения, которое может быть получено путем вращения половины круга его диаметра, как оси (рис. 81).
Определения этих фигур из курса геометрии средней школы:
Цилиндр – тело, которое состоит из двух кругов (оснований), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Конус – тело, которое состоит из круга (основания), точки (вершины), не лежащей в плоскости этого круга, и всех отрезков, соединяющих вершину конуса с точками основания.
Шар – тело, которое состоит из всех точек пространства, находящихся на расстоянии не более заданного (радиуса) от данной точки (центра).
Рис. 79 Рис. 80 Рис. 81
Задание 48
- Высоты цилиндра и прямого цилиндра;
- Образующей конуса, высоты конуса и прямого конуса.
Знакомство с объемными фигурами расширяет знания детей об окружающем мире, закладывает основы для изучения геометрии в школе, обогащает их речь, формирует навыки обследования, развивает мышление.
Опорный конспект к теме

Вопросы для самоконтроля
1. Что изучает геометрия?
2. Что изучает планиметрия?
3. Что изучает стереометрия?
4. Что называется геометрической фигурой?
5. Назовите правила построения геометрии.
6. Назовите основные фигуры на плоскости и в пространстве.
7. Какие фигуры называются плоскими?
8. Какие фигуры называются выпуклыми?
9. Дайте определение отрезка.
10. Дайте определение луча.
11. Дайте определение угла.
12. Какая линия называется ломаной?
13. Какая ломаная называется простой?
14. Дайте определение многоугольника.
15. Какой многоугольник называется выпуклым?
16. Какой многоугольник называется правильным?
17. Дайте определение треугольника.
18. Какой треугольник называется равносторонним, какой – равнобедренным, какой – разносторонним?
19. Какой треугольник называется прямоугольным, какой – тупоугольным, какой – остроугольным?
20. Дайте определение выпуклого четырехугольника.
22. Дайте определение круга и окружности.
23. Дайте определение многогранника.
24. Какой многогранник называется выпуклым?
25. Какой выпуклый многогранник называется правильным?
26. Назовите все правильные выпуклые многогранники и дайте им определение.
27. Дайте определение призмы. Изобразите любую призму.
28. Дайте определение прямоугольного параллелепипеда и изобразите его.
29. Дайте различные определения куба и изобразите его.
30. Дайте определение пирамиды. Изобразите любую пирамиду.
31. Дайте два определения цилиндра и изобразите его.
32. Дайте два определения конуса и изобразите его.
33. Дайте два определения шара и изобразите его.
34. Что такое сфера?
Задания для самостоятельной работы
1. Придумайте для дошкольников или младших школьников задания с геометрическими фигурами, которые предполагают их объединение, пересечение, дополнение.
2. Придумайте задания для дошкольников или младших школьников и приведите примеры диалогов с детьми, в процессе которых раскрываются существенные свойства понятий: круг, треугольник, квадрат, прямоугольник, четырехугольник, многоугольник.
3. Придумайте игровые упражнения и диалоги к ним для детей (возраст определите сами) на распознавание геометрических тел: куба, прямоугольного параллелепипеда, пирамиды, конуса, цилиндра, шара.
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.017)
Читайте также:

