Взаимное расположение двух прямых на плоскости кратко

Обновлено: 02.07.2024

Прямые, находящиеся в одной плоскости, будут либо пересекающимися, либо параллельными. Выясним условия, при которых прямые соответствуют тому или иному случаю, определим угол между прямыми, координаты точки пересечения, если таковая имеется.

Пусть две прямые заданы уравнениями

Поскольку угловой коэффициент определяет наклон прямой к оси абсцисс, то очевидно, что равные углы наклона соответствуют параллельным прямым. Поэтому условием параллельности двух прямых, заданных уравнениями (4.1) является равенство их угловых коэффициентов

Если , то угол между прямыми (4.1) определяется известной тригонометрической формулой тангенса разности двух углов , которое в случае прямых принимает вид

Если прямые (4.1) перпендикулярны, т.е. , то

условие перпендикулярности двух прямых.

Если прямые заданы общими уравнениями

то указанные выше условия будут выглядеть так:

условие параллельности ; (4.6)

условие перпендикулярности ; (4.7)

угол между прямыми . (4.8)

определяет совпадающие прямые.

Точка пересечения двух прямых (4.5) есть общая точка этих прямых. Координаты этой точки должны одновременно удовлетворять уравнениям обеих прямых, т.е. системе

Решая эту систему, находим координаты искомой точки.

Замечание. Для определения угла между прямыми, удобнее переходить к уравнению с угловым коэффициентом.

Пример 1. Напишите уравнение медианы АМ треугольника АВС, если заданы координаты его вершин А(-5;4), В(3;1), С(2;-5).

Решение. Точка М − середина отрезка ВС, поэтому в соответствии с формулами (2.5) ; ; М(2,5;-2). Уравнение прямой АМ запишем, используя формулу (3.1): или , , . Разделив обе части уравнения на 1,5, получим более удобный вид − уравнение медианы АМ.

Пример 2. Напишите уравнение прямой , проходящей через точку М(7;4) параллельно прямой .

Решение. Первый способ. Согласно формуле (3.5), уравнение любой прямой, проходящей через точку М, может быть записано в виде . Поскольку искомая прямая должна быть параллельна прямой , то их угловые коэффициенты совпадают. Запишем в виде уравнения прямой с угловым коэффициентом , откуда . Следовательно, искомая прямая имеет уравнение или .

Второй способ. Будем искать уравнение прямой в виде . Поскольку прямая проходит чрез точку М(7;4), то координаты этой точки удовлетворяют уравнению. И можно записать . Данная прямая параллельна прямой , для которой , . Подставив эти значения в предыдущее уравнение, получим , . Окончательно запишем, что уравнение искомой прямой имеет вид .

Замечание. Если дано общее уравнение прямой , то уравнение параллельной прямой, проходящей через заданную точку х₁, у₁, имеет вид

Пример 3. Проверить, принадлежит ли точка М(2;-4) прямой .

Решение. Подставим координаты точки М в левую часть уравнения прямой . Поскольку левая часть не равна правой: , то точка М не принадлежит прямой .

Пример 4. На прямой найти точку, у которой ордината .

Решение. Подставив в уравнение прямой значение найдем абсциссу : ; . Искомая точка .

Пример 5. Найти координаты вершин параллелограмма , если известны координаты вершины , а также уравнение сторон : и : .

Решение. Решая эту задачу, необязательно (и даже не нужно) рисовать данные в условии прямые и точки в декартовых координатах. Достаточно (для себя) нарисовать произвольный параллелограмм, чтобы определиться с расположением вершин и сторон (рис. 6). Окончательный чертеж можно выполнить после получения решения.

Поскольку , то, используя условие параллельности двух прямых (4.11), можно записать , − уравнение прямой DC. Прямая AD, заданная уравнением , параллельна оси ОХ . И поскольку точка принадлежит прямой ВС, то уравнение полностью определяет эту прямую. Теперь, когда известны уравнения всех сторон параллелограмма, его вершины найдем из решения систем вида (4.10). Точка А − пересечение прямых АВ и AD:

Точка В − пересечение прямых АВ и ВС:

Точка − пересечение прямых AD и DC:

Ответ: координаты точек , , .

Пример 6. Найти уравнение прямой , проходящей через точку М(1;1), перпендикулярно прямой .

Решение. Перепишем уравнение в виде . Таким образом, угловой коэффициент данной прямой . Если прямая, проходящая через точку М, перпендикулярна данной, то их угловые коэффициенты связаны соотношением (4.4): , откуда . В соответствии с формулой (3.5), можно записать уравнение искомой прямой , проходящей через точку М(1;1) перпендикулярно прямой или ; .

Ответ: уравнение прямой .

Пример 6.1. Найти расстояние от точки М(1;1) до прямой .

Решение. Расстоянием d от точки до прямой называется длина перпендикуляра, опущенного из точки М на прямую. Поэтому сначала запишем уравнение прямой, проходящей через точку М перпендикулярно данной прямой. Эта часть задания нами уже выполнена в примере 6, поэтому воспользуемся готовым результатом и запишем, что нужная нам прямая имеет уравнение . Найдем точку А пересечения прямых и , решая систему ; ; . Расстояние между точками А и М вычислим по формуле (2.1): .

Ответ: расстояние от точки М до прямой d=1.

Замечание. Можно вывести формулу расстояния от точки до прямой в общем случае, используя рассуждения примера 6.1. Тогда получим формулу

Пример 7. Через точку провести прямую под углом к прямой .

Решение. Обозначим прямую как , а искомую прямую, проходящую через точку М, как . Уравнение прямой, проходящей через точку М, имеет вид (см. формулу (3.5)): или . Здесь − угловой коэффициент прямой . Записав уравнение прямой в виде , найдем ее угловой коэффициент . Поскольку известен угол между прямыми, то согласно формуле (4.3) ; ; ; . Теперь окончательно запишем уравнение искомой прямой или .

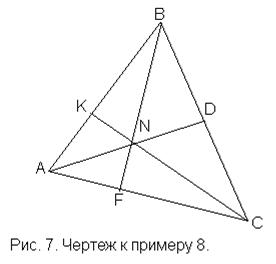
Пример 8. Даны две вершины треугольника и . Его высоты пересекаются в точке . Определить координаты третьей вершины треугольника .

Решение. Для удобства рекомендуется нарисовать произвольный треугольник АВС (рис. 7).

Пусть AD, BF и CK – высоты треугольника АВС, N – точка пересечения высот. В связи с этим AN и AD определяют одну и ту же прямую. Аналогично для пар BN и BF, а также CN и CK. Согласно формуле (3.1) уравнение прямой BN (или, что то же самое, прямой BF: ; ; ; − прямая BF. Аналогично, уравнение прямой AN (или AD): ; − прямая AD.

Запишем уравнение стороны ВС как уравнение прямой, проходящей через точку В, перпендикулярно прямой AD. Поскольку AD определяется уравнением y=const, то перпендикулярная ей прямая ВС будет иметь уравнение x=const. А так как эта прямая проходит через точку В, то абсцисса точки В и определит уравнение ВС: х=6.

Уравнение стороны АС запишем как уравнение прямой, проходящей через точку А перпендикулярно прямой BF, согласно формулам (4.4) и (3.5). Так как угловой коэффициент BF известен: , то угловой коэффициент АС – это , поэтому уравнение АС: ; − уравнение АС.

Точка С теперь может быть найдена как пересечение прямых ВС
и АС: ; ; .

Пусть две прямые заданы уравнениями

Если прямые (4.1) перпендикулярны, т.е. , то

условие перпендикулярности двух прямых.

Если прямые заданы общими уравнениями

то указанные выше условия будут выглядеть так:

условие параллельности ; (4.6)

условие перпендикулярности ; (4.7)

угол между прямыми . (4.8)

определяет совпадающие прямые.

Решая эту систему, находим координаты искомой точки.

Замечание. Для определения угла между прямыми, удобнее переходить к уравнению с угловым коэффициентом.

Пример 1. Напишите уравнение медианы АМ треугольника АВС, если заданы координаты его вершин А(-5;4), В(3;1), С(2;-5).

Пример 2. Напишите уравнение прямой , проходящей через точку М(7;4) параллельно прямой .

Пример 3. Проверить, принадлежит ли точка М(2;-4) прямой .

Пример 4. На прямой найти точку, у которой ордината .

Решение. Подставив в уравнение прямой значение найдем абсциссу : ; . Искомая точка .

Точка В − пересечение прямых АВ и ВС:

Точка − пересечение прямых AD и DC:

Ответ: координаты точек , , .

Пример 6. Найти уравнение прямой , проходящей через точку М(1;1), перпендикулярно прямой .

Ответ: уравнение прямой .

Пример 6.1. Найти расстояние от точки М(1;1) до прямой .

Ответ: расстояние от точки М до прямой d=1.

Пример 7. Через точку провести прямую под углом к прямой .

Решение. Для удобства рекомендуется нарисовать произвольный треугольник АВС (рис. 7).

Точка С теперь может быть найдена как пересечение прямых ВС
и АС: ; ; .

Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.

Прямая на плоскости – понятие

Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.

Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Взаимное расположение прямой и точки

На каждой прямой и в каждой плоскости могут быть отмечены точки.

Точки обозначают как большими, так и маленькими латинскими буквами. Например, А и D или a и d .

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Данное высказывание считается акисомой, поэтому не требует доказательств. Если рассмотреть это самостоятельно, видно, что при существующих двух точках имеется только один вариант их соединения. Если имеем две заданные точки А и В , то прямую, проходящую через них можно назвать данными буквами, например, прямая А В . Рассмотрим рисунок, приведенный ниже.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Краткая запись принадлежности включает в себя использование знаков ∈ и ∉ . Для того, чтобы зафиксировать расположение отрезка относительно заданной прямой, применяют ⊂ . Если в условии дано, что отрезок А Р принадлежит прямой b , значит, и запись будет выглядеть следующим образом: А Р ⊂ b .

Случай принадлежности одновременно трех точек одной прямой имеет место быть. Это верно, когда одна точка лежит между двумя другими. Данное утверждение принято считать аксиомой. Если даны точки А , В , С , которые принадлежат одной прямой, а точка В лежит между А и С , следует, что все заданные точки лежат на одной прямой, так как лежат по обе стороны относительно точки B .

Точка делит прямую на две части, называемые лучами. Имеем аксиому:

Любая точка O , находящаяся на прямой, делит ее на два луча, причем две любые точки одного луча лежат по одну сторону луча относительно точки O , а другие – по другую сторону луча.

Взаимное расположение прямых на плоскости

Расположение прямых на плоскости может принимать вид двух состояний.

Две прямые на плоскости могут совпадать.

Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.

Две прямые на плоскости могут пересекаться.

Данный случай показывает, что имеется одна общая точка, которую называют пересечением прямых. Вводится обозначение пересечение знаком ∩ . Если имеется форма записи a ∩ b = M , то отсюда следует, что заданные прямые a и b пересекаются в точке M .

При пересечении прямых имеем дело образовавшимся углом. Отдельному рассмотрению подвергается раздел пересечения прямых на плоскости с образованием угла в 90 градусов, то есть прямого угла. Тогда прямые называют перпендикулярными. Форма записи двух перпендикулярных прямых такая: a ⊥ b , а это значит, что прямая a перпендикулярна прямой b .

Две прямые на плоскости могут быть параллельны.

Только в том случае, если две заданные прямые не имеют общих пересечений, а, значит, и точек, они параллельны. Используется обозначение, которое можно записать при заданной параллельности прямых a и b : a ∥ b .

Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.

Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.

Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.

Для этого приводим необходимы факторы, доказывающие их взаимное расположение:

если две прямые параллельны третьей, тогда они все параллельны;
если две прямые перпендикулярны третьей, тогда эти две прямые параллельны;
если на плоскости прямая пересекла одну параллельную прямую, тогда пересечет и другую.

Рассмотрим это на рисунках.

Способы задания прямой на плоскости

Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.

Прямая задается при помощи указанных двух точек, расположенных в плоскости.

Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.

Прямая может быть задана через точку и прямую, которой она параллельна.

Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.

Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.

Прямая задается через указанную точку и направляющий вектор.

Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.

Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:

Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.

И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.

В данной публикации мы рассмотрим, из себя представляет прямая (на плоскости), перечислим ее основные свойства, а также приведем варианты взаимного расположения двух прямых.

Определение прямой

Прямая – это не искривляющаяся линия, которая не имеет ни начала, ни конца. Обычно обозначается двумя общепринятыми способами:

Взаимное расположение прямых

Если мы рассматриваем две прямые на плоскости, то они могут по-разному располагаться по отношению друг к другу:

Примечание: в трехмерном пространстве прямые могут быть скрещивающимися, т.е. лежащими в разных плоскостях.

Свойства прямой

Через любую точку можно провести бесконечное количество прямых.
Через любые две точки, которые не совпадают, можно провести прямую, причем только одну.
Две прямые на плоскости являются либо параллельными, либо пересекающимися (в т.ч. перпендикулярными).
Если две любые точки прямой лежат на определенной плоскости, значит все точки данной прямой принадлежат этой же плоскости.

Если две прямые лежат на плоскости, то возможны три различных случая взаимного расположения их: 1) прямые пересекаются (т. е. имеют одну общую точку), 2) прямые параллельны и не совпадают, 3) прямые совпадают.

Выясним, как узнать, какой из этих случаев имеет место, если прямые заданы своими уравнениями

Если прямые пересекаются, т. е. имеют одну общую точку, то координаты этой точки должны удовлетворять обоим уравнениям (15). Следовательно, для нахождения координат точки пересечения прямых нужно решить совместно их уравнения. С этой целью исключим сначала неизвестное х, для чего умножим первое уравнение на , а второе на А, и вычтем первое из второго. Будем иметь:

Чтобы исключить из уравнений (15) неизвестное у, умножим первое из них на а второе на и вычтем второе из первого. Получим:

Если то из уравнений (15) и (15") получим решение системы (15):

Формулы (16) дают координаты х, у точки пересечения двух прямых.

Таким образом, если то прямые пересекаются. Если то формулы (16) не имеют смысла. Как в этом случае располагаются прямые? Легко видеть, что в этом случае прямые параллельны. Действительно, из условия следует, что (если же , то прямые параллельны оси Оу и, следовательно, параллельны между собой).

Итак, если то прямые параллельны. Рассматриваемое условие можно записать в виде можно сказать, что если в уравнениях прямых соответствующие коэффициенты при текущих координатах пропорциональны, то прямые параллельны.

В частности, параллельные прямые могут совпадать. Выясним, каков аналитический признак совпадения прямых. Для этого рассмотрим уравнения (15) и ). Если свободные члены этих уравнений будут оба равны нулю, т. е.

т. е. коэффициенты при неизвестных и свободные члены уравнений (15) пропорциональны. В таком случае одно из уравнений системы получается из другого умножением всех его членов на некоторый общий множитель, т. е. уравнения (15) равносильны. Следовательно, рассматриваемые параллельные прямые совпадают.

Если же хотя бы один из свободных членов уравнений (15) и ) будет отличен от нуля (или или

то уравнения (15) и (15"), а значит и уравнения (15), не будут иметь решений (по крайней мере одно из равенств (15) или (15") будет невозможным). В этом случае параллельные прямые не будут совпадать.

Итак, условием (необходимым и достаточным) совпадения двух прямых является пропорциональность соответствующих коэффициентов их уравнений:

Пример 1. Найти точку пересечения прямых линий

Решая уравнения совместно, умножим второе на 3:

Вычитая, получим: откуда Умножая первое уравнение на 3, второе на 2 и вычитая первое второго, получим: откуда координаты точки пересечения двух данных прямых суть:

Существует три варианта взаимного расположения двух прямых в пространстве: прямые могут
быть пересекающимися, параллельными и скрещивающимися. Изучение этих положений необходимо в начертательной геометрии.

Пересекающиеся прямые

Две различные (то есть не совпадающие) прямые, имеющие единственную общую точку, называются пересекающимися.

Если две прямые имеют две общие точки, то они совпадают.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

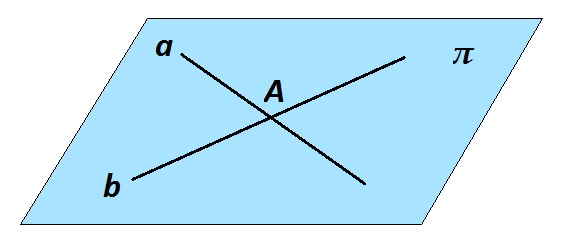
На рисунке изображены прямые a и b, которые пересекаются в точке А. Через две пересекающиеся прямые проходит плоскость, причем только одна.

Параллельные прямые

На плоскости прямые параллельны, если они не пересекаются. То есть главный признак — это отсутствие общих точек. Однако для параллельности в пространстве этого условия недостаточно.

Две прямые в пространстве параллельны, если они обе лежат в одной плоскости и не пересекаются. Два отрезка, лежащие на параллельных прямых, также параллельны.

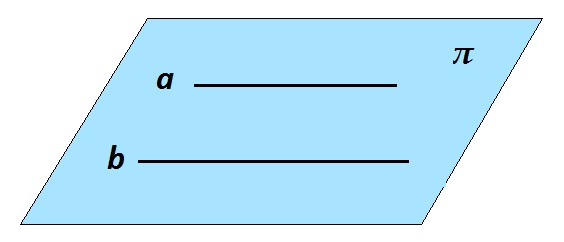
На рисунке a || b, через них проходит единственная плоскость.

Две различные прямые, параллельные третьей прямой, параллельны между собой.

В виде формулы это выглядит так: a||b, b||c ⇒ a||c.

Скрещивающиеся прямые

Через две пересекающиеся или параллельные прямые можно провести плоскость, и притом единственную. Возможна также ситуация, когда через две прямые плоскость провести нельзя.

Две прямые называются скрещивающимися, если они не параллельны и не пересекаются.

Другими словами, две прямые скрещиваются, если они не лежат в одной плоскости, так как прямые, лежащие в одной плоскости, обязательно будут либо пересекаться, либо параллельны.

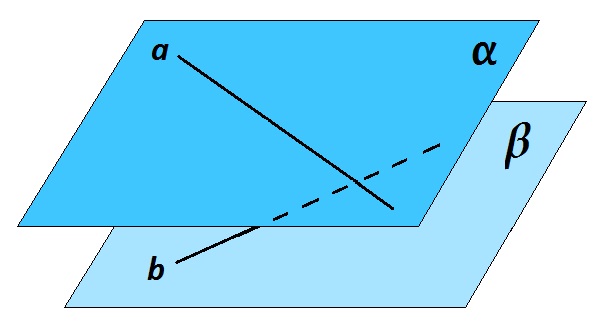
Прямые a и b на рисунке скрещиваются. Важно, что через две скрещивающиеся прямые можно провести две параллельные плоскости. Причем это единственная пара плоскостей.

Если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые — скрещивающиеся.

Доказательство:

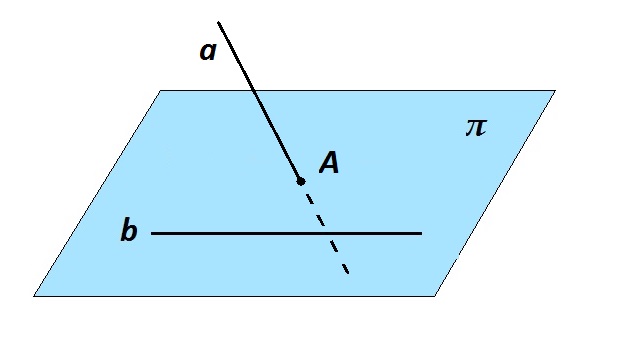
Пусть a и b — прямые, b лежит в плоскости π, a пересекает плоскость π в точке A. А не принадлежит прямой b. Используем метод доказательства от противного. Предположим, что прямые a и b лежат в одной плоскости. В этом случае данная плоскость проходит через прямую b и точку А, то есть она совпадает с плоскостью π.
Прямая a не может одновременно находиться в плоскости π и пересекать ее в одной точке, как дано по условию. Теорема доказана.

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство:

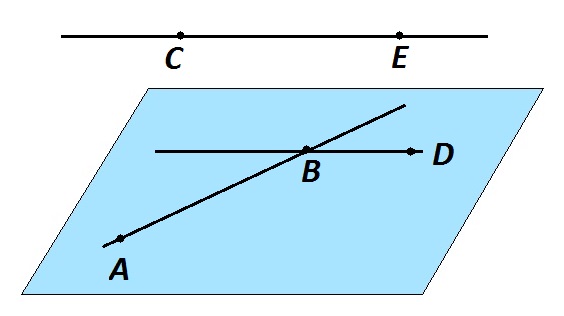
Рассмотрим скрещивающиеся прямые AB и CЕ.

Через точку D можно провести прямую ВD параллельную СЕ.
Через пересекающиеся прямые BD и AB можно провести плоскость.
Так как прямая CE не лежит в этой плоскости и параллельна прямой BD, то она параллельна и данной плоскости. Эта плоскость единственная.

Полуплоскости. Сонаправленные лучи

Любая прямая делит плоскость на две полуплоскости.

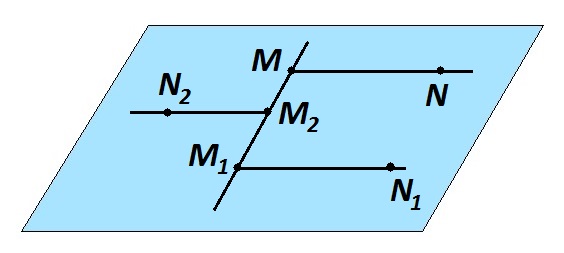
Лучи называют сонаправленными, если они лежат в одной полуплоскости и параллельны.

Параллельные и лежащие в разных полуплоскостях лучи не являются сонаправленными. На рисунке лучи MN и \(M_1N_1 \) — сонаправленные, а MN и \(M_2N_2, M_1N_1\) и \(M_2N_2\) — параллельны, но не сонаправлены.

Два угла равны, если две их стороны соответственно сонаправлены.

Доказательство:

Приведем доказательство для углов, лежащих в разных плоскостях. Изобразим ∠А и \(∠А_1 \) на чертеже.

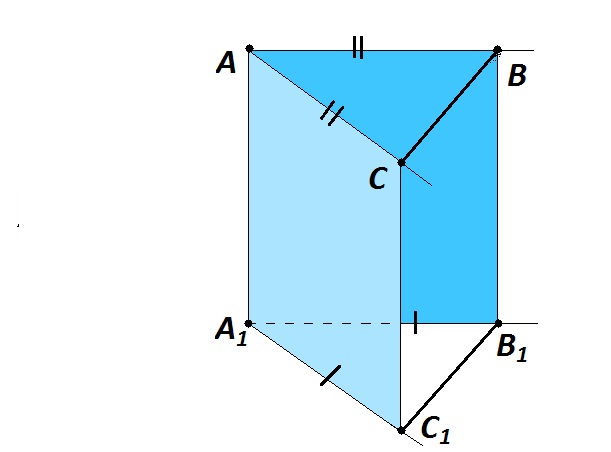
Сонаправленные лучи параллельны ⇒ соответственно параллельны стороны углов. Так как через параллельные прямые можно провести единственную плоскость, проведем через них две плоскости. На сторонах угла А и угла А1 отметим точки С, В и С1, В1 соответственно — так, чтобы \(АС=А_1С_1\) и \(АВ=А_1В_1\) . Получившаяся объемная фигура имеет вид треугольной призмы.
У полученного четырехугольника \(AВВ_1A_1\) противолежащие стороны AВ и \(A_1В_1\) равны и параллельны по условию. Это значит, что \(AВВ_1A_1\) — параллелограмм. \(AA_1 =ВВ_1, AA_1||ВВ_1\) .
Аналогично выясним, что \(AСС_1A_1\) — параллелограмм, и \(СС_1=АА_1, СС_1||АА_1\) .
\(СС_1\) и \(BB_1\) равны и параллельны третьему отрезку \(АА_1\) , следовательно: они равны и параллельны между собой, т. е. \(СС_1||BB_1\) и \(СС_1= BB_1\) . Значит \(ВСС_1В_1\) — параллелограмм, и из этого получаем: \(ВС=В_1С_1\) .
Так как \(АВ=А_1В_1, AС =A_1С_1\) и \(СB=С_1B_1\) , выясняем, что ΔABС и \(ΔA_1B_1С_1\) равны по трем сторонам, и поэтому \(А=А_1.\)

Угол между прямыми

Свойство пересекающихся прямых

Если две любые прямые лежат в одной плоскости и пересекаются, то они образуют четыре неразвернутых угла. Если известен один из этих углов, то можно найти и другие три угла. Углом между прямыми называют тот из углов, который не больше любого из трех остальных, очевидно, что он больше 0° и меньше либо равен 90°.

Угол между скрещивающимися прямыми

Угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, параллельными заданным скрещивающимся прямым.

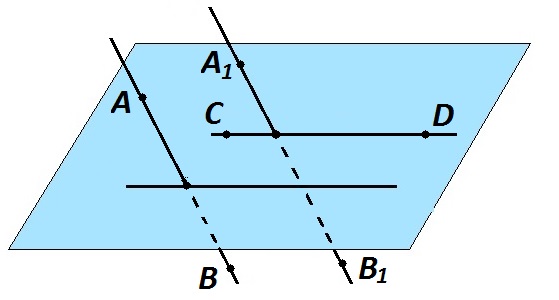
Угол между скрещивающимися прямыми АВ и СD равен \(∠А_1СD\) между \(А_1В_1\) и СD, если \(АВ||А_1В_1.\)

Читайте также: