Уравнение шредингера химия кратко
Обновлено: 02.07.2024
Благодаря толкованию волн, изложенному де Бройлем, и соотношению неопределенностей Гейзенберга можно придти к тому, каким должно быть уравнение движения в рамках теории квантовой механики. Это должно быть равенство, которое описывает движения микрочастиц в силовом поле и из которого были бы видны волновые свойства частиц, наблюдаемые экспериментально. Также оно должно являться уравнением по отношению к волновой функции, поскольку вероятность, с которой частица пребывает в некоторый момент времени в объеме d V в области с координатами x y z , описывается с помощью именно этой величины. Поскольку нужное уравнение иллюстрирует волновые свойства частиц, то он должно само быть волновым уравнением (точно так же, как и уравнение, описывающее электромагнитную волну).
История появление теории
В 1962 г. Шредингер сформулировал положение, позже названное основным уравнением в нерелятивистской квантовой механике, или волновым уравнением Шредингера.
Эрвин Шредингер ( 1887 - 1961 , Австрия) был одним из физиков-теоретиков, которые основали квантовую механику. Он является автором трудов по статистической физике, квантовой теории, биофизике, а также общей теории относительности. Сформулировал основы теории движения микрочастиц – волновой механики (волновая теория Шредингера), а также квантовой теории возмущений (похожий метод в квантовой механике). Лауреат Нобелевской премии.
Отличительной особенностью уравнения Шредингера является то, что оно постулируется, а не выводится. Его истинность подтверждена экспериментально, следовательно, оно может считаться законом природы.
В наиболее общем виде его записывают так:
- h 2 m ∇ 2 Ψ + U ( x , y , z , t ) Ψ = i h ∂ 2 Ψ ∂ t 2 .
Здесь m обозначает массу частицы, i 2 - мнимую единицу, ∇ – так называемый оператор Лапласа, равный ∇ 2 Ψ = ∂ 2 Ψ ∂ x 2 + ∂ 2 Ψ ∂ y 2 + ∂ 2 Ψ ∂ z 2 , Ψ – искомую волновую функцию, а выражение U ( x , y , z , t ) соответствует потенциальной энергии частицы в определенной точке силового поля.
Описание движения частицы в потенциальном поле
Если поле, в котором происходит движение частицы, является потенциальным, то функция U не будет иметь явно выраженной зависимости от времени, и ей можно придать смысл потенциальной энергии. Тогда решить уравнение Шредингера можно разделением на сомножители: один из них будет зависеть только от времени, а второй – только от координаты точки.
Ψ ( x , y , z , t ) = Ψ ( x , y , z ) e - i E h t .
Параметр E обозначает полную энергию частицы. Если поле стационарное, то значение E остается постоянным. Подставив это значение в выражение выше, мы можем убедиться в его справедливости. При этом у нас получится формула Шредингера для стационарных состояний:
- h 2 2 m ∇ 2 Ψ + U Ψ = E Ψ .
∇ 2 Ψ + 2 m h 2 ( E - U ) Ψ = 0 .
Также данное выражение может быть записано в следующем виде:
Преобразование уравнения выполнено с использованием оператора Гамильтона H ^ . Его можно найти, сложив значения операторов - h 2 2 m ∇ 2 + U = H ^ . Гамильтониан – это оператор потенциальной энергии E .
Квантовая механика использует различные операторы также и в качестве других переменных, особенно динамических. Существуют операторы импульса, момента импульса, координат и т.д.
Основная идея волновой механики заключается в том, что для таких малых тел, как электрон, нельзя с определенностью сказать, где оно находится в данное время и куда направляется. Можно установить только относительную вероятность его нахождения в том или ином месте и наличие определенного количества движения в определенный момент времени.
В 1924 г. де Бройль предположил, что точно также, как свет, который, как обычно считают, имеет волновую природу, на самом деле при определенных обстоятельствах ведет себя, как будто он состоит из частиц – квантов, - так и очень малые частицы, такие, как электроны, также могут обладать волновыми свойствами. Де Бройль предположил, что с пучком электронов следует связывать длину волны, определяемую уравнением
где $\hbar$ – постоянная Планка ($6,626\cdot 1034 Дж\cdot с$ или $6,626\cdot 10-27 эрг\cdot с$), а $p$ – количество движения (импульс) электрона в пучке, т.е. его масса, умноженная на его скорость.
Физическое подтверждение волновой природы электрона было продемонстрировано в 1927 – 1928 гг. Дейвиссоном, Джермером и Томсоном, которые показали, что пучок электронов может испытывать дифракцию на подходящей решетке (атомы в кристалле золота), аналогичную дифракции пучка света.

Рисунок 1. Дифракция пучка электронов
На преграду с двумя узкими щелями направлен параллельный пучок моноэнергетических (т.е. обладающих одинаковой кинетической энергией) электронов (рис. 1. а). За преградой находится фотопластина $Фn$. При закрытии щели номер $2$ и экспонировании в течение времени $t$ почернение на проявленной фотопластине будет характеризоваться кривой $1$ (рис. 1. б). При закрытии щели номер $1$, соответственно, почернение на фотопластине будет соответствовать кривой $2$. Однако в случае, когда открыты обе щели картина почернения фотопластины (рис. 1. в) отнюдь не эквивалентна наложению двух первых картин. Зато она аналогична картине, получающейся при интерференции двух когерентных световых волн.
Готовые работы на аналогичную тему
Тот факт, что системы малых частиц проявляют, по крайней мере, при определенных условиях, волновые свойства, предполагает возможность описания таких систем уравнениями, подобными те, которые описывают другие виды волнового движения, например, волны, которые распространяются вдоль колеблющейся струны, или волновое движение, приписываемое электромагнитному излучению. Действительно, можно начать с волнового уравнения, соответствующего электромагнитным волнам, и путем определенных замен, превратить его в уравнение, соответствующее нашему случаю. Хотя эти замены диктуются физическими причинами, они в основном произвольны и могут быть приняты только потому, что приводят к уравнению, которое, как показывает опыт, позволяет получить правильное решение физических задач. Поэтому следует принять волновое уравнение как постулат, так как у химиков основной интерес вызывает применение волнового уравнения к атомным и молекулярным системам, а не физические и математические соображения, которыми руководствовался Шредингер, впервые его предложивший в 1925 г.
Общий вид уравнения Шредингера

Рисунок 2. Эрвин Шрёдингер (1887 - 1961)
Волновое уравнение, применяемое для расчета стационарных состояний системы, можно записать в символическом виде:
где $H$ представляет собой определенный способ выражения общей энергии системы, а $E$ – числовое значение этой энергии. Для всех систем, которые обычно интересуют химиков, общая энергия представляет собой сумму кинетической энергии $Т$ и потенциальной энергии $V$:
Это соотношение было широко использовано физиком-теоретиком Гамильтоном, поэтому $H$ часто называют функцией Гамильтона, а $\mathcal H$ гамильтонианом системы.
Уравнение Шредингера на примере атома водорода
Рассмотрим модель атома водорода, предложенную Бором. Для простоты предположим, что тяжелое ядро закреплено (оно почти, но не совершенно неподвижно, когда электрон движется вокруг него). Тогда полная кинетическая энергия $Т$ системы представляет собой просто кинетическую энергию электрона
где $m$ – масса электрона и $\nu$ – его скорость. Потенциальная энергия системы есть просто энергия, возникающая вследствие электростатического взаимодействия (гравитационные силы приблизительно в $10^$ раз меньше), и ее можно выразить как
где $e$ - заряд электрона, $r$ - радиус орбиты, знак минус появляется вследствие того, что заряд одной из частиц положителен $(+)$, а другой отрицателен $(-)$. Поэтому для атома водорода функция Гамильтона в классической (т.е. доквантовомеханической) физике равна:
Если использовать понятие количества движения электрона $p=m\nu$, данное уравнение запишется в следующем виде:
Теперь для перехода от классического описания этой или какой-либо другой системы к описанию при помощи волновой механики, необходимо взять функцию Гамильтона (уравнение 6) и произвести в ней определенные замены: в функции Гамильтона количество движения следует заменить выражением
Таким образом, гамильтониан для атома водорода в его квантовомеханической форме $<\mathcal H>$ следует записать в виде
Если теперь это выражение гамильтониана подставить в общее волновое уравнение (уравнение 1), то получим:
Это и есть волновое уравнение для атома водорода. Из уравнения 9 следует, что нужно вторые производные функции $\psi $ сложить и умножить на $-<<\hbar >^2>/<8<\pi >^2m>$, затем к этому добавить $\left(-/\right)\psi $, тогда получим величину, тождественную Е$\psi $. Если найдена функция $\psi $, то говорят, что она является решением волнового уравнения, и ее называют волновой функцией. Вообще, может быть несколько различных функций $\psi_1$, $\psi_2$, . , $\psi_n$, которые являются решениями уравнения 9, причем каждой соответствует свое значение энергии $Е_1$, $Е_2$, . , $Е_n$.

Уравнение Шредингера имеет большое значение для квантовой механики — наряду со вторым законом Ньютона в классической механике или уравнением Максвелла для изучения природы электромагнитных волн. Закономерности, описанные ученым, объясняют движение частиц, скорость которых существенно меньше, чем скорость света.
Общее уравнение Шредингера — какой имеет вид и зачем нужно
Уравнением Шредингера называют линейное дифференциальное равенство с частными производными, которое описывает изменение в пространстве и во времени чистого состояния посредством волновой функции в гамильтоновых квантовых системах.
Опытным путем можно наблюдать волновые свойства частиц. Определение данного явления является следствием уравнения, которое описывает движение микроскопических частиц в разных силовых полях. Закономерности движения в квантовой механике вытекают из статистического толкования волн де Бройля и соотношения неопределенностей Гейзенберга.
Главное уравнение представляет собой формулу относительно волновой функции \(\psi\) (x, y, z,t). Это объясняется тем, что \(\left|\psi \right|\) является определением вероятности присутствия частицы в определенное время t в объеме ΔV, то есть в области со следующими координатами:
Основная закономерность нерелятивистской квантовой механики была представлена в 1926 году Э. Шредингером. Данная формула не является выводом, это — постулат. Справедливость уравнения подтверждается согласием с результатами опыта, что говорит о природном характере выявленной закономерности.
Общее уравнение Шредингера обладает следующим видом:
где ħ равно отношению \(\frac<2\pi >\)
m — является массой частицы,
Δ — оператор Лампаса,
i — представляет собой мнимую единицу,
U(x, y, z, t) — равно потенциальной функции частицы в силовом поле, в котором она движется,
\(\psi\) (x, y, z, t) — служит искомой волновой функцией частицы.
Данная формула справедлива для любых частиц, спин которых равен нулю, движущихся с небольшой скоростью относительно скорости света. Уравнение можно дополнить условиями, характерными для волновой функции:
- волновая функция имеет конец, однозначна и непрерывна;
- производные волновой функции отличаются непрерывностью;
- \(\left|\psi \right|\) интегрируема, что является условием нормировки вероятностей.
В первом случае описано уравнение, которое зависит от времени. Многие физические явления, наблюдаемые в микромире, можно охарактеризовать с помощью упрощенной формулы. При исключении зависимости волновой функции от времени можно определить закономерность Шредингера для стационарных состояний, то есть состояний, в которых значения энергии фиксированы. Такие ситуации возможны при стационарном силовом поле, в котором происходит движение частицы. Таким образом, функция U = U (x, y, z) не определяется временем и обладает смыслом потенциальной энергии.
В данном случае уравнение Шредингера будет иметь следующий вид:
\(\Delta \psi +\frac>\left(E-U \right)\times \psi =0\)
Данная формула получила название уравнения Шредингера для стационарных состояний. Здесь используют полную энергию Е-частицы. Согласно теории дифференциальных уравнений доказано, что имеется бесчисленное множество решений подобных уравнений, которые имеют физический смысл при отборе методом наложения граничных условий. В случае уравнения Шредингера такими условиями являются характеристики регулярности волновых функций:
- конечность волновых функций;
- однозначность и непрерывность волновых функций наряду с первыми производными.
Реальным физическим смыслом обладают лишь те решения, которые определены регулярными функциями $$\left|\psi \right|$$. Регулярные решения характерны не для любых значений величины Е, а лишь при конкретной их совокупности в рамках определенной задачи. Такие параметры энергии носят название собственные. В свою очередь решения с собственными значениями энергии определяют как собственные функции. С помощью собственных параметров Е формируют непрерывный или дискретный ряд. Для первого случая характерен непрерывный или сплошной спектр, для второго — дискретный спектр.
Применение уравнения Шредингера
Уравнение Шредингера не подходит для описания следующих явлений:
- Спонтанное излучение, в связи с тем, что волновая функция для возбужденного состояния представляет собой точное решение уравнения Шредингера с учетом зависимости от времени.
- Процесс изменения, характерный для квантовой механики, так как уравнение линейно, детерминистично и обладает обратимостью во времени, а данный процесс не отличается линейностью, стохастичен и необратим.
- Взаимное превращение элементарных частиц, по причине описания данных процессов релятивистской квантовой теорией поля.
Можно рассмотреть применение уравнения Шредингера к свободной частице или электрону, который совершает движение вдоль оси ОХ. При этом величина потенциальной энергии частицы, находящейся в свободном движении, равна нулю. То есть U = 0. Тогда уравнение Шредингера будет иметь следующий вид:
Исходя из гипотезы Бройля, можно смоделировать перемещение такого микроскопического объекта с помощью плоской монохроматической волны, занимающей все пространство:
Волновая функция, характеризующая движение свободной частицы вдоль оси ОХ, бедт записана следующим образом:
где \(\psi _\) является амплитудой волны.
Круговая частота \(\omega\) и волновое число k связаны с полной энергией E и импульсом р следующими закономерностями:
Из данных соотношений следует:
В таком случае волновая функция будет иметь следующий вид:
Продемонстрировать соответствие данного вида функции уравнению Шредингера можно, если определить \(\Delta \psi\) и \(P^\)
Далее необходимо определить \(\frac
Используя отношение энергии частицы Е к импульсу p, получим формулу:
Подставив данные значения в уравнение, можно вывести следующее равенство:
Данное равенство соответствует уравнению Шредингера, когда U=0. Корректный вид волновой функции можно обосновать для случая движения частицы в силовом поле, в случае, когда потенциальная энергия не равна нулю. Формула будет иметь следующий вид:
Такое уравнение характеризует энергию движения частицы по аналогии с кинетической энергией в классической механике. После подстановки значений Е и Р уравнение приобретает следующий вид:
Конечная формулировка идентична уравнению Шредингера. Данное выражение применимо для частицы, которая совершает движение в силовом поле.
Пример решения уравнения Шредингера
Задание 1
Электрон движется в одном измерении вдоль оси ОХ между двумя потенциальными барьерами. В случае, если высота барьеров на концах ямы не имеет ограничений, электрон, как и в атоме, совершает финитное движение. Необходимо описать движение в квантовой механике и поведение импульса и энергии частицы.
Решение
Вначале следует изобразить ситуацию схематично
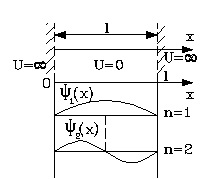
Согласно условиям задачи, функция U(x) обладает особым, разрывным видом и равна нулю в области между стенками. На краях ямы, то есть на ее барьерах, функция будет бесконечна:
При х=0 и х=l \(U=\propto\)
Уравнение Шредингера для стационарных состояний частиц, находящихся между барьерами, имеет следующий вид:
Выполняя преобразования в формулах, получим:
К полученной формуле следует прибавить граничные условия на барьерах ямы. Необходимо учесть связь волновой функции и вероятности нахождения частиц. Согласно условиям задания, частица за пределами стенок не находится. В таком случае значение волновой функции на стенках и за их пределами равно нулю. Граничные условия задания будут иметь следующий вид:
При дальнейших действиях нужно учитывать, что решением последней формулы являются волны де-Бройля. Одну волну де-Бройля в качестве решения к задаче не применить, так как с ее помощью заранее описывается свободная частица, движущаяся в одном направлении. В данном случае рассматривается движение частицы между стенками. Поэтому, используя принцип суперпозиции, в решении можно применить две волны де-Бройля, совершающих движение навстречу друг к другу с импульсами р и –р. Формула будет иметь следующий вид:
\(\psi =C_\times exp\left(\fracpx \right)+C_\times exp\left(-\fracpx \right)\)
Исходя из граничных условий и условий нормировки, можно определить постоянные \(С_1\) и \(С_2\) . Сумма всех вероятностей позволит рассчитать вероятность нахождения электрона между стенками в любом месте и получить единицу, то есть значение вероятности достоверного события равна 1. Уравнение будет иметь такой вид:
Исходя из первых граничных условий:
Решение задачи будет иметь следующий вид:
\(\psi =C\times \left(exp\left(\fracpx \right)-exp\left(-\fracpx \right) \right)\)
\(exp\left(\fracpx \right)-exp\left(-\fracpx \right) =2\sin \frac\)
Постоянная А выходит из условий нормировки. В данном случае она не представляет интереса. Необходимо использовать второе граничное условие. Тогда решение можно записать в виде уравнения:
Импульс при этом принимает только определенные значения:
Следует учесть, что n не равно нулю. Это объясняется тем, что в противном случае волновая функция повсюду имела нулевые значения. В этом случае для частицы между стенками состояние покоя не характерно. Электрон обязательно должен совершать движение. Минимальное значение возможного импульса движущейся частицы равен:
Ранее было указано, что импульс электрона изменяет знак во время отражения от барьеров. В этом заключается сложность представления ответа на вопрос, каков импульс у частицы, запертой между стенками. Он может быть равен –р или +р. Импульс не определен. Степень неопределенности будет выражаться в следующем:
Неопределенность координаты Δх равна l. Обнаружить частицу можно в пределах между барьерами. Точное местонахождение электрона неизвестно. Наименьшее значение импульса имеет вид:
Исходя из этого условия, можно вывести равенство:
\(\Delta x\times \Delta p_=h\)
Таким образом, соотношение Гейзенберга в рамках данной задачи, то есть при наличии наименьшего значения р, подтверждено. В случае произвольно-возможного значения импульса соотношение неопределенности приобретает такой вид:
\(\Delta x\times \Delta p_\geq h\)
Согласно исходному постулату Гейзенберга-Бора о неопределенности Δх и Δу, установлена лишь нижняя граница неопределенностей, возможная при измерениях. В начале движения наблюдают минимальные неопределенности, которые возрастают со временем. Полученное уравнение демонстрирует следующее: импульс системы в квантовой механике не всегда изменяется непрерывно. Спектр импульса электрона в данном случае дискретный, импульс частицы между барьерами изменяется скачкообразно. Величина такого скачка при условиях задания является постоянной величиной и определяется как:
Можно изобразить спектр возможных значений импульса электрона. Дискретность изменения механических величин, не применимая к классической механике, в квантовой механике является следствием ее математического аппарата. Невозможно представить наглядное объяснение скачкообразного изменения импульса. Это закон квантовой механики, данный вывод следует из него логически и является объяснением.
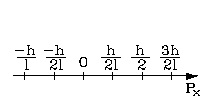
Далее необходимо обратиться к энергии электрона. Данная величина обладает связью с импульсом. В случае дискретного спектра импульса получают дискретный спектр значений энергии частицы между барьерами. Подставив ранее известные формулы в уравнение, получим:
где n = 1, 2,…, представляет собой квантовое число.
Таким образом, получают энергетические уровни.
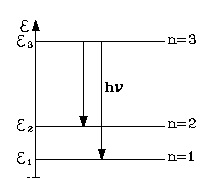
На рисунке представлены энергетические уровни, согласно условию задания. Если изменить их, то схема расположения энергетических уровней будет изменена. В случае, когда частица обладает зарядом, как электрон, и расположена на самом низком энергетическом уровне, она будет в состоянии спонтанно испускать свет, как фотон. При этом переход на более низкий энергетический уровень возможен с условием:
Для этого задания волновые функции, характерные каждому стационарному состоянию, являются синусоидами. Их нулевые значения будут отмечены на стенках.
Уравнение Шредингера имеет огромное значение для развития современной науки. Квантовая механика является популярной дисциплиной для изучения в специализированных вузах. Нередко студенты учебных заведений сталкиваются со сложными задачами, решение которых отыскать порой достаточно сложно.
При возникновении трудностей в образовательном процессе получить квалифицированную помощь можно с помощью сервиса Феникс.Хелп.
Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.
Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.
где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.
Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.
Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).
Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.
Читайте также:

