Третий признак равенства треугольников доказательство кратко

Обновлено: 05.07.2024

Дано:

Приложим треугольник A₁B₁C₁ к треугольнику ABC так, чтобы

вершина A₁ совместилась с вершиной A,
вершина B₁ совместилась с вершиной B,
точки C₁ и C лежали по разные стороны от прямой AB.

При этом возможны три случая взаимного расположения луча CC₁ и угла ACB.

I. Луч CC₁ проходит внутри угла ACB.

Проведём отрезок CC₁.

По условию AC=A₁C₁ и BC=B₁C₁, поэтому треугольники ACC₁ и BCC₁ — равнобедренные с основанием CC₁.

Если к равным углам прибывать равные углы, то получим равные углы:

Таким образом, ∠ACB=∠AC₁B.

Точки A₁ и A, B₁ и B совмещены, то есть ∠AC₁B и ∠A₁C₁B₁ — один и тот же угол.

Для треугольников ABC и A₁B₁C₁ имеем:

Следовательно, ΔABC= ΔA₁B₁C₁ (по 1 признаку равенства треугольников).

II. Луч CC₁ проходит внутри угла ACB.

Так как AC=A₁C₁ и BC=B₁C₁, треугольники ACC₁ и BCC₁ — равнобедренные с основанием CC₁ и ∠ACC₁=∠AC₁C и ∠BCC₁=∠BC₁C (как углы при основании).

Если из равных углов вычесть равные углы, то получим равные углы:

III. Луч CC₁ совпадает со стороной угла ACB.

По условию BC=B₁C₁, поэтому треугольник BCC₁ — равнобедренный с основанием CC₁.

Отсюда ∠C₁=∠C (как углы при основании) и ΔABC= ΔA₁B₁C₁ (по 1 признаку равенства треугольников).

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

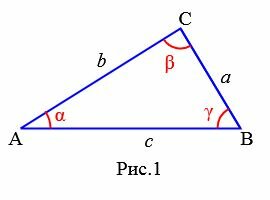Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

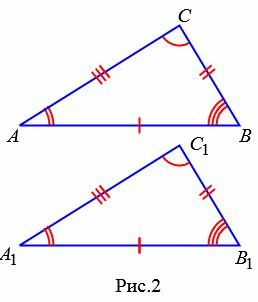
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

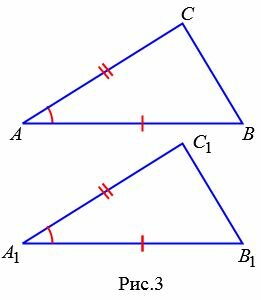Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Так как ∠A=∠A₁, то треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины A и A₁ совпадали, а стороны AB и AС наложились на лучи A₁B₁ и A₁C₁, соответственно.

Так как по условию теоремы AB=A₁B₁, AС=A₁С₁, то сторона AB совместится со стороной A₁B₁, а сторона AС − со стороной A₁С₁.Тогда совместятся B и B₁, C и С₁. Следовательно сторона BC совместится со стороной B₁C₁. То есть треугольники ABC и A₁B₁C₁ полностью совместятся. Теорема доказана.

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

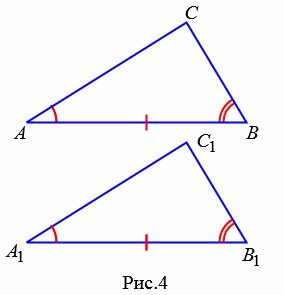Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Наложим треугольник ABC на треугольник A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, сторона AB − со стороной A₁B₁ (по условию теоремы AB=A₁B₁), а вершины C и С₁ оказались по одну сторону от прямой A₁B₁.

Так как ∠A=∠A₁ и ∠B=∠B₁, то сторона AС наложится на луч A₁C₁ а сторона BС − на луч B₁С₁. Тогда вершина C окажется на луче A₁C₁ и на луче B₁C₁. Т.е. она окажется на пересечении этих лучей и, следовательно, вершина C совместится с общей точкой лучей A₁C₁ и B₁C₁, т.е. с вершиной C₁. Таким образом совместятся стороны AC и A₁C₁, BC и B₁C₁. То есть треугольники ABC и A₁B₁С₁ полностью совместятся, поэтому они равны. Теорема доказана.

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

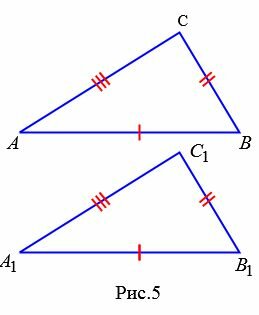Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

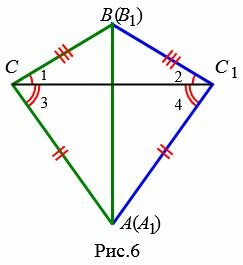Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

Вариант 1 (Рис.6). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и ∠3=∠4 и, следовательно:

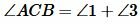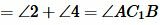Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

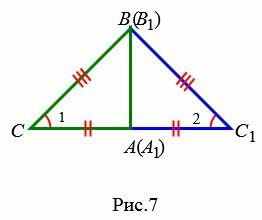Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

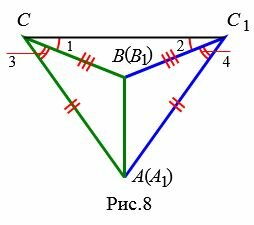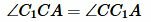
Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

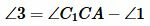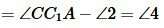Имеем AC=A₁C₁, BC=B₁C₁ и по первому признаку равенства треугольников . Теорема доказана.

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

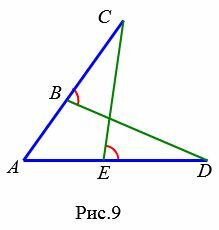Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

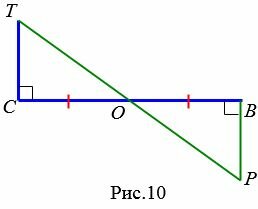Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

Соединим подвинем, повернём треугольники равными сторонами AC и A1C1. Один из треугольников отразим сверху вниз. Затем соединим точки B и B1 отрезком .

Первое доказательство третьего признака равенства треугольников

В треугольнике ABB1 стороны AB и AB1 равны. Следовательно треугольник ABB1 равнобедренный , и его углы при основании — равны. Эти углы ABB1 и AB1B помечены одной дужкой.

В треугольнике CBB1 стороны CB и CB1 равны, следовательно треугольник CBB1 равнобедренный , и его углы при основании — равны. Эти углы CBB1 и CB1B помечены двойной дужкой.

У нас получилось, что углы ABC и A1B1C1 равны, так как они сложены из одинаковых углов. И следовательно исходные треугольники равны по двум сторонам и углу между ними. Что и требовалось доказать.

ABC = A₁B₁C₁, так как AC = A₁C₁, AB =A₁B₁ и BC =B₁C₁.

Из данной теоремы следует, что треугольник - жесткая фигура, т.е. фигура, не подверженная деформации.

Доказательство:

Дано: ABC, A₁B₁C₁, AC = A₁C₁, AB =A₁B₁, BC =B₁C₁.

Доказать: ABC = A₁B₁C₁

Доказательство:

Приложим ABC к A₁B₁C₁ так, чтобы вершина A совместилась с вершиной A₁, вершина B - с вершиной B₁, а вершины C и C₁ оказались по разные стороны от прямой AB (A₁B₁).

1. Луч CC₁ проходит внутри A₁C₁B₁.

2. Луч CC₁ совпадает с одной из сторон A₁C₁B₁.

3. Луч CC₁ проходит вне A₁C₁B₁.(обратите внимание, что, несмотря на то, что изображения в п.2 и в п.3 похожи, эти два случая для различных треугольников)

Рассмотрим последний случай (остальные доказываются аналогично): Поскольку по условию теоремы AC = A₁C₁, BC =B₁C₁, то CB₁C₁ и CA₁C₁ - равнобедренные. По теореме о свойстве углов равнобедренного треугольника B₁CC₁ = B₁C₁C, A₁CC₁ = A₁C₁C. Следовательно, B₁CA₁ = B₁C₁A₁ (B₁CA₁ = B₁CC₁ - A₁CC₁ = B₁C₁C - A₁C₁C = B₁C₁A₁). Таким образом, AC = A₁C₁, BC = B₁C₁, B₁CA₁ = B₁C₁A₁ , а из этого следует, что ABC = A₁B₁C₁ по I признаку равенства треугольников, что и требовалось доказать.

Читайте также: