Теория информации шеннона кратко

Обновлено: 04.07.2024

ИНФОРМАЦИИ ТЕОРИЯ – раздел математики, исследующий процессы хранения, преобразования и передачи информации. В основе его лежит определенный способ измерения количества информации. Возникшая из задач теории связи, теория информации иногда рассматривается как математическая теория систем передачи информации. Опираясь на основополагающую работу К.Шеннона (1948), теория информации устанавливает основные границы возможностей систем передачи информации, задает исходные принципы их разработки и практического воплощения. В настоящей статье рассматривается ядро теории информации – свойства информационных мер и их приложения к анализу систем передачи информации.

Кодирование.

Источник информации можно представить в виде случайной величины X, принимающей одно из конечного числа возможных значений m> с вероятностью p_i (p_i – вероятность того, что X = i). Энтропия случайной величины X по определению равна

где логарифмы берутся по основанию 2 и энтропия измеряется в битах. Такое определение энтропии связано с определением энтропии в термодинамике. Энтропия устанавливает нижнюю границу средней длины любого двоичного представления случайной величины.

Рассмотрим случайную величину X, принимающую значения a, b, c> с вероятностями ( 1 /₂, 1 /₄, 1 /₄). Код для этой случайной величины мог бы иметь вид (0, 10, 11). Увидев строку 01001110, получатель мог бы однозначно разбить ее на 0, 10, 0, 11, 10, что декодируется в строку a, b, a, c, b>, причем необходимости в специальном символе для обозначения конца кодированного слова не возникает. Заметим, что средняя длина такого кода составляет ( 1 /₂ ×1) + ( 1 /₄ ×2) + ( 1 /₄ ×2) = 1,5 бита, т.е. совпадает с энтропией источника.

Один из основных результатов теории информации связан с теоремой, согласно которой выборочную случайную величину можно представить без ошибки с помощью H + 1 бита и невозможно представить источник без ошибки с помощью менее, чем H битов. Отсюда следует, что энтропия является фундаментальным ограничением для представления источника информации, и мы можем найти представления со средней длиной в пределах одного бита энтропии. Оптимальное представление случайной величины (в терминах средней длины) может быть найдено с помощью алгоритма Хаффмана. Этот алгоритм позволяет строить коды для источников с энтропией, не превышающей одного бита.

Теоретически можно вычислить коэффициент энтропии случайного процесса, моделирующего источник информации, а затем найти представления, не превышающие один бит энтропии. Однако многие встречающиеся на практике источники информации обладают структурой, которую очень трудно представить в рамках простой модели. Примером источника, который исследовали многие авторы, служит английский текст. Попытаемся оценить коэффициент энтропии английского языка с помощью различных моделей.

Для простоты предположим, что английский алфавит состоит из 26 букв и одного пробела. В простейшей модели все знаки равновероятны. Можно показать, что энтропия такой модели равна log 27 = 4,76 бита на букву. Но в реальном английском языке буквы не равновероятны (например, буква E встречается с большей вероятностью, чем Q). Используя относительные частоты различных букв для вычисления энтропии, мы получили бы оценку около 4,03 бита на букву. Таков был бы коэффициент энтропии, если бы буквы английского алфавита встречались независимо друг от друга.

Но это не так. Например, за буквой Q почти всегда следует U, и т.д. Воспользовавшись условными распределениями, мы могли бы построить более точную оценку коэффициента энтропии английского языка. Например, если воспользоваться моделью, в которой каждая буква зависит только от предыдущей, то получится оценка примерно в 3,3 бита на букву. Рассматривая распределение букв, которое зависит от трех предыдущих букв, мы получаем оценку примерно в 2,8 бита на букву.

Однако всю сложность зависимостей, существующих в реальном английском языке, ни одна из этих моделей полностью не передает. Зато играя в игру, аналогичную игре в 20 вопросов, и состоящую в угадывании следующей буквы, можно получить гораздо более точные оценки коэффициента энтропии английского языка. Эксперименты с образцами английских текстов показывают, что коэффициент энтропии немного больше, чем 1 бит на букву. Это означает, что в английском языке существует значительная избыточность, которую можно устранить с помощью подходящего кодирования. Например, не составляет никакого труда декодировать следующее английское предложение:

TH. . R. . S . NLY . N. W. Y

T. F. LL . N TH. V. W. LS

IS ONLY ONE WAY

FILL IN THE VOWELS

Сложность по Колмогорову.

Каналы связи.

До сих пор мы рассматривали сложность описания источника информации и показали, что естественной мерой этой сложности служит коэффициент энтропии случайного процесса, моделирующего источник. Рассмотрим теперь проблему передачи этого описания по каналу связи. Примерами каналов связи могут служить телеграфные и телефонные провода, передающие информацию посредством электрических сигналов. В сотовых телефонах информация передается с помощью электромагнитного излучения.

Вместо того, чтобы заниматься конкретными деталями той или иной системы связи, мы можем построить ее общую модель. Это делается заданием списков возможных входных и выходных символов, а также функции распределения вероятностей, указывающей вероятность различных возможных выходных символов для каждого возможного входного символа. В простейшем случае выходной сигнал канала равен входному сигналу, и любая поступающая на вход информация без ошибок передается на выход. Например, если бы у нас был канал, который мог бы передавать два символа, и оба они принимались на выходе без ошибки (рис. 2), то с каждым символом мы могли бы передавать один бит информации. Такие каналы получили название каналов без шума. Их пропускная способность равна максимальному количеству информации, которое может поступить на вход. Если канал имеет N возможных входных символов, то его пропускная способность равна log N битов за передачу. Если такой канал может передавать 1 символ в секунду, то его пропускная способность равна log N битов в секунду.

В приведенном выше примере двоичного канала его пропускная способность составляет 0,53 бита на передачу. Таким образом, с помощью 100-кратного повторения мы можем передать по этому каналу 53 бита информации с пренебрежимо малой вероятностью ошибки.

Поскольку теорема Шеннона о пропускной способности канала связи в чем-то противоречит нашей интуиции, попытаемся понять, почему эта теорема верна. Рассмотрим канал, изображенный на рис. 4. В этом канале существует 10 возможных входных символов, обозначенных цифрами 0, 1, 2, ј , 9, и десять возможных выходных символов. Каждый входной символ с равной вероятностью порождает выходной символ, обозначенный либо той же цифрой, либо на единицу больше. Например, цифра 3 на входе с равной вероятностью порождает на выходе 3 или 4, а цифра 9, соответственно, – 9 или 0. Поэтому, обнаруживая на выходе канала цифру 5, мы не можем однозначно утверждать, была ли передана цифра 5 или 4.

Если мы ограничим множество входных символов четными числами, т.е. 0, 2, 4, 6 и 8, то при любом выходном символе без всякой неопределенности или ошибки сможем указать соответствующий входной символ. Таким образом, используя лишь некоторое подмножество возможных входных символов, мы можем передавать информацию без ошибок. Скорость, с которой мы можем передавать информацию по этому каналу, равна log 5 битов на передачу. Можно показать, что эта скорость оптимальна и совпадает с пропускной способностью канала, изображенного на рис. 4.

В общем случае пропускная способность канала определяется разностью между безусловной энтропией выхода канала и условной энтропией канала с заданным входным сигналом. Эта величина называется взаимной информацией между входом и выходом канала; максимум взаимной информации по всем распределениям вероятностей входа является пропускной способностью канала. Если распределение вероятностей, которому подчиняется канал, известно, то эта величина может быть вычислена.

Такой непрерывный канал служит полезной моделью многих широко используемых на практике каналов радио- и телефонной связи.

Коэффициент энтропии источника и пропускная способность канала связаны основной теоремой теории информации, которая гласит: кодирующие и декодирующие устройства, позволяющие безошибочно воссоздавать входной сигнал на выходе, могут быть построены в том и только в том случае, если коэффициент энтропии источника меньше пропускной способности канала. Теория информации ничего не говорит нам о том, как именно такие кодирующие и декодирующие устройства можно сконструировать, она лишь говорит о возможности их существования в принципе, если предположить, что их сложность может быть сколь угодно велика. Создание таких устройств составляет предмет теории кодирования, ставшей самостоятельной наукой со своими методами и важными результатами. Для создания практических кодирующих и декодирующих устройств были разработаны различные тонкие алгебраические методы. Широкому распространению таких кодов способствовали и успехи в развитии технологии интегральных схем. Например, в плейерах для проигрывания компакт-дисков используется один из видов кодов, исправляющих ошибки, который называется кодом Рида – Соломона и способен исправлять до 4000 следующих подряд ошибок.

Последние достижения в области теории информации несколько расширили понятия пропускной способности и сжатия данных на случай сетей каналов связи. Прогресс в теории кодирования позволил создавать модемы для телефонных каналов, вплотную приблизившие скорость передачи информации к их пропускной способности. Универсальные алгоритмы сжатия данных типа алгоритма Лемпеля – Зива ныне широко используются для сжатия компьютерных файлов. Теория информации остается активно развивающейся областью исследований, поставляющей в наш информационный век новые идеи и подходы в сферу проектирования и анализа систем передачи данных и компьютерных систем.

Шеннон К. Работы по теории информации и кибернетике. М., 1963
Колмогоров А.Н. Проблемы передачи информации. М., 1965
Яглом А.М., Яглом И.М. Вероятность и информация. М., 1973
Галлагер Р. Теория информации и надежная связь. М., 1974
Чисар И., Кернер Я. Теория информации: теоремы кодирования для дискретных систем без памяти. М., 1985

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?

Это не столько о самой информации, сколько о передаче информации. То есть о коммуникации.

Теория оказала огромное влияние на современное общество, и все еще существуют безграничные возможности для размышлений и исследований. Рассмотрим три основных составляющих этой теории:

1. Единая структура коммуникации

Следует отметить, что информация в теории Шеннона НЕ равнозначна смыслу. Безнадежный бред, например, это тоже информация, потому что человек, слышащий ее, не знал этого раньше. То же самое с честным броском монеты.

2. Как передавать больше информации и быстрее

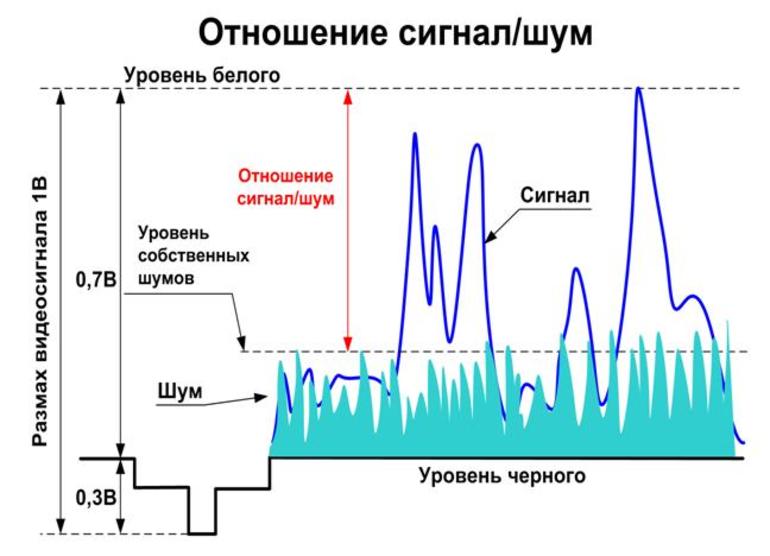
Кроме того, надо учитывать некоторый уровень шума (помех) в канале связи. Шум может возникать во многих формах. В случае телефонного звонка, это фоновый шум, который отвлекает человека на другой линии.

Как же бороться с шумом и снизить риск сбоя связи? Добавляя избыточность обратно !

Информационная теория

Обработка информации — важная техническая задача, чем, например, преобразование энергии из одной формы в другую. Важнейшим шагом в развитии теории информации стала работа Клода Шеннона (1948). Логарифмическое измерение количества данных было первоначальной теорией, и прикладными задачами по коммуникации в 1928 году. Наиболее известным является вероятностный подход к измерению информации, на основе которого представлен широкий раздел количественной теории.

Отличительная черта вероятностного подхода от комбинаторного состоит в том, что новые предположения об относительной занятости любой системы в разных состояниях и общего количества элементов не учитываются. Ряд информации взят из отсутствия неопределённости в выборе различных возможностей. В основе такого подхода лежат энтропийные и вероятностные множества.

Основная теорема Шеннона о кодировании

Важный практический вопрос при обработке информации — какова мощность системы передачи данных. Можно получить определённый ответ, используя уравнение Шеннона. Оно позволяет точно понять информационную пропускную способность любого сигнального канала. Формула Шеннона в информатике: I = — (p1log2 p1 + p2 log2 p2 +. + pN log2 pN)

Не существует метода кодирования, который бы позволял передавать со скоростью, превышающей vzm, и с произвольно низкой вероятностью ошибки. Другими словами, если поток информации: H '(Z) = vz * H (Z) C он не существует.

Это приводит к замечательному выводу:

Сигнал, который эффективно передаёт информацию, будет меняться и непредсказуем.
Эффективный сигнал очень похож на случайный шум.

Передача сигналов

Это означает:

Определённое уравнение

Сигнал и шум не коррелированны, то есть они не связаны каким-либо образом, который позволит предсказать один из них. Суммарная мощность, получаемая при объединении этих некоррелированных ИС, по-видимому, случайно изменяющихся величин, задаётся.

Поскольку сигнал и шум статистически аналогичны, их комбинация будет иметь то же значение форм-фактора, что и сам сигнал или шум. Потому можно ожидать, что комбинированный сигнал и шум, как правило, будут ограничены диапазоном напряжения.

Стоит рассмотреть теперь разделение этого диапазона на полосы одинакового размера. (т. е. каждая из этих полос будет охватывать ИС.) Чтобы предоставить другую метку для каждой полосы, нужны символы или цифры. Поэтому всегда можно указать, какую полосу занимает уровень напряжения в любой момент с точки зрения B-разрядного двоичного числа. По сути, этот процесс является ещё одним способом описания того, что происходит, когда берут цифровые образцы с B-разрядным аналоговым преобразователем, работающим в общем диапазоне.

Нет никакого реального смысла в выборе значения, которое настолько велико. Это потому что шум кубика будет просто иметь тенденцию рандомизировать фактическое напряжение на эту сумму, делая любые дополнительные биты бессмысленными. В результате максимальное количество битов информации, которую можно получить относительно уровня в любой момент, будет определено.

Уравнение Шеннона может использовать:

Максимально возможную скорость передачи информации по заданному каналу или системе.
Передачу данных определяется полосой пропускания, уровнем сигнала и шума.
Поэтому ИС называется законом информационной пропускной способности канала.

При передаче информации некоторые параметры используемых сигналов могут приобретать случайный символ в канале связи, например, из-за многолучевого распространения радиоволн, гетеродинирующих сигналов. В результате амплитуда и начальная фаза данных являются случайными. Согласно статистической теории связи, эти особенности сигналов необходимы для их оптимальной обработки, они определяют как структуру приёмника, так и качество связи.

Помехи разложения всегда присутствуют в границе любого реального сигнала. Однако, если их уровень настолько мал, что вероятность искажения практически равна нулю, можно условно предположить, что все сигналы передаются неискажёнными.

В этом случае средний объём информации, переносимой одним символом, можно считать расчётным: J (Z; Y) = Хапр (Z) — Хапест (Z) = Хапр (Y). Поскольку функция H (Y) = H (Z) и H (Y / Z) = 0, а индекс max = Hmax (Y) — максимальная энтропия источника класса сигнала, возникающая в результате распределения символов Y: p (y1) = p (y2) = … = p (ym) = 1 / My, т. е. Hmax (Y) = logaMy.

Следовательно, главная дискретная ширина полосы таблицы без информации о помехах в единицу времени равна: Cy = Vy • max = Vy • Hmax (Y) = Vy • logaMy или записываться Ck = Vk • logaMy. Где буква Mk — должно быть максимально возможное количество уровней, разрешённых для передачи по этому каналу (конечно, может обозначаться Mk = My).

Согласно теореме, метод кодирования онлайн, который может использоваться и позволяет:

с данными согласно уравнению H (x) ≤ C — передать всю информацию, сгенерированную источником с ограниченным размером буфера калькулятора;
в случае H (x)> C такого способа кодирования не существует, поскольку требуется буфер, объём которого определяется избыточной производительностью источника по ширине полосы канала, умноженной на время передачи.

Вероятностный подход к определению вычисления объёма информации — математический вывод формулы Шеннона не является удовлетворительным для метода оценки роли энтропии, отражения элементов системы и может не применяться. Как общий информатический объект невозможно допустить единый способ измерения и его правила.

Кто же такой Клод Шеннон? Каждая комната в Entropy House, поместье неподалеку от Бостона, где Шеннон вместе с женой Бетти прожили более 30 лет, может ответить на этот вопрос по-разному. Одна комната, опрятная и аккуратная, украшена рядами наград, демонстрирующих многочисленные достижения хозяина дома. В их числе Национальная научная медаль, полученная им в 1966 году, Премия Киото — японский эквивалент Нобелевской — и Медаль Почёта IEEE.

Любовь Шеннона к математическим абстракциям и всевозможным устройствам проявилась в раннем возрасте. Он родился в 1916 году в пригороде Гейлорда, штат Массачусетс, и провел там значительную часть детства. Шеннон обожал играть со всевозможными радио-наборами — их покупал ему отец. Еще Шеннону очень нравилось решать математические головоломки, которые задавала ему сестра, будущая профессор математики.

В 1941 году Шеннон устроился в Bell Laboratories и проработал там 15 лет. Во время Второй мировой войны он участвовал в разработке цифровых систем шифрования. Одной из них пользовались Черчилль и Рузвельт для проведения трансокеанских переговоров.

Как говорит сам Шеннон, эта работа и привела к появлению теории коммуникации. Он понял, что при помощи числовых кодов можно защитить информацию от чужих глаз. Соответственно, и от помех тоже. Кроме того, эти коды можно использовать для эффективного упаковывания информации и дальнейшей передачи по выделенному каналу.

Аарон Уайнер, руководитель отдела исследований в области коммуникационного анализа AT&T Bell Laboratories заметил, что некоторые научные открытия являются продуктом своего времени, но не лично Шеннона.

Только в начале 1970-х годов с появлением высокоскоростных интегральных схем инженеры начали полноценно пользоваться теорией информации. В наши дни идеи Шеннона применяются практически во всех системах, которые хранят, обрабатывают или передают информацию в цифровом виде, от компакт-дисков до суперкомпьютеров, от факсимильных аппаратов до зондов для исследования дальнего космоса, таких как Voyager.

Теория информации и религия

Теория информации с самого начала пленила аудиторию, намного более широкую, нежели та, для которой она была предназначена. Специалисты в лингвистике, психологии, экономике, биологии, даже музыканты и художники стремились объединить теорию информации со своими дисциплинами.

Шеннон, хотя и скептически относился к некоторым применениям своей теории, не был ограничен в собственных изысканиях. В 1950-х годах в своей гостиной он проводил эксперименты на тему избыточности языка. В них участвовала его жена Бетти, работавшая в Bell, Бернард Оливер, еще один ученый из Bell (а также бывший президент IEEE), а также жена Оливера. Кто-то называл первые буквы слова или слов в предложении, а все остальные пытались угадать продолжение. Другой эксперимент Шеннон поставил в Bell Laboratories. Сотрудники должны были подсчитать, сколько раз в письме появлялись различные буквы, и каков порядок их появления.

Понимая, что технологии 50-х не позволяли провернуть нечто подобное, редактор все равно связался с Шенноном. В ответ он рассмеялся и рассказал, как провел многих людей по всей стране. Шторы вокруг стола с лабиринтом скрывали механизм от зрителей и были важным компонентом устройства. Когда в 1979 году Spectrum торжественно вручал награды Amazing Micromouse Maze Contest, Шеннон снял Тесея со своего чердака, погрузил его в машину и выставил на витрине рядом с механизмом-победителем.

Единая полевая теория жонглирования

В 1956 году Шеннон оставил постоянную должность в Bell Labs (но еще более десяти лет работал внештатно), чтобы стать профессором коммуникационных наук в MIT. В последние годы его новой великой страстью стало жонглирование. Он построил несколько жонглирующих машин и разработал единую полевую теорию жонглирования: если B равно числу шаров, H — числу рук, D — времени, которое каждый шар проводит в руке, F — времени полета каждого шара и E — времени, когда каждая рука пуста, то B / H = (D + F) / (D + E).

(К сожалению, теория не могла помочь Шеннону жонглировать более чем четырьмя шарами одновременно. Он говорил, что его руки слишком малы.)

Шеннон также разработал множество математических моделей для прогнозирования роста акций и протестировал их — успешно, по его словам, — на своем собственном портфеле.

“Respect your cube and keep it clean./Lube your cube with Vaseline./Beware the dreaded cubist’s thumb,/The callused hand and fingers numb./No borrower nor lender be./Rude folk might switch two tabs on thee,/The most unkindest switch of all,/Into insolubility. [Chorus] In-sol-u-bility./The strangest place to be./However you persist/Solutions don’t exist.”

Уважь свой кубик, в чистоте
Держи его и смажь везде.
Но бойся тех, кто этот куб,
Не выпускал всю жизнь из рук.
Не отдавай свой кубик. Вот —
Его сломает обормот.
Предмет — странней не видел свет,
Собрать его ни шанса нет!
[Припев]
Не-раз-ре-шимый куб,
Пусть даже ты не глуп.
Из кожи лезешь, но
Не сможешь все равно.

В конце концов Шеннон произнес вдохновляющую речь, в которой предвосхитил идеи об универсальности обратной связи и самореференциальности в природе.

Тем не менее, Шеннон снова исчез из виду. Лишь в последние годы жена вдохновила его на посещение небольших собраний и различных лабораторий, где ученые работают с его теорией.

В 1985 году он неожиданно приехал на Международный симпозиум по теории информации в Брайтоне. Встреча шла своим чередом ровно до того момента, как прошел слух, что седой мужчина с застенчивой улыбкой, который появляется то там, то здесь, это Клод Шеннон. А ведь некоторые из гостей конференции даже не знали, что он все еще жив.

Клод Шеннон умер в 2001 году в возрасте 84 лет после многих лет борьбы с болезнью Альцгеймера и по праву считается одним из величайших инженеров электроники всех времен.

Теория информации — раздел прикладной математики, радиотехники (теория обработки сигналов) и информатики, относящийся к измерению количества информации, её свойств и устанавливающий предельные соотношения для систем передачи данных.

Теория информации изучает вопросы измерения, хранения и передачи информации.

Появление дисциплины теории информации в основном связывают с публикацией в июле и октябре 1948 года в журнале Bell System Technical Journal статьи Клода Шеннона “Математическая теория коммуникации”.

В этой революционной работе впервые представлена качественная и количественная модель связи в виде статистического процесса. Эта модель собственно стала основой теории информации.

Вследствие появления модели связи, появились так же понятия

информационной энтропии и избыточности источника; Теорема Шеннона о кодировании источника
взаимной информации и пропускной способности зашумлённого канала; Теоремы Шеннона для канала с шумами
теоремы Шеннона-Хартли о предельной пропускной способности зашумлённого канала с гауссовским шумом
количественной меры информации

Некоторые из старейших методов связи неявно использовали многие идеи, которые впоследствии будут строго определены в теории информации. Например, в телеграфии используется азбука Морзе, в которой более распространённые буквы имеют более короткие коды, чем менее распространённые буквы. Кодирование информации таким образом является основной идеей, используемой при сжатии данных без потерь.

Прямыми предшественниками работ Шеннона были две работы, опубликованные в 1920-х годах Гарри Найквистом и Ральфом Хартли.

Статья Найквиста 1924 года “Определённые факторы, влияющие на скорость телеграфа” в основном посвящена некоторым подробным техническим аспектам телеграфных сигналов. Однако в более теоретическом разделе рассматривается количественная оценка “сведений” и “линейной скорости”, с которой они могут передаваться через коммуникационную систему в виде

\[W=K\log m,\] где \(W\) - скорость передачи данных, \(m\) - количество различных уровней напряжения на выбор на каждом шаге, а \(K\) - постоянная.

В работе Хартли 1928 года, называвшейся просто “Передача информации”, было использовано слово “информация” (в техническом смысле), и было чётко указано, что информация в этом контексте является измеримой величиной, отражающей только способность получателя отличать одну последовательность символов от любой другой - независимо от любого связанного значения или других психологических или семантических аспектов, которые они могут представлять. Это количество информации, которую он определил как

\[H=\log S^,\] где S - количество возможных символов, а n - количество символов в передаче. Естественной единицей информации, таким образом, была десятичная цифра.

Аналогичные единицы вероятности были введены Аланом Тьюрингом в 1940 году в рамках статистического криптоанализа немецкой шифровальной машины Enigma.

Однако в основе всех этих понятий по-прежнему лежала идея равной априорной вероятности, а не информационного содержания событий с различной вероятностью.

Областью, в которой активно изучалась неравномерность вероятностей, являлась статистическая механика. В частности, Людвиг Больцманн в контексте своей H-теоремы 1872 года впервые представил количественную меру

\[ H=-\sum f_\log f_\] в качестве меры широты распространения состояний, доступных для одной частицы в газе таких же частиц, где f представляет собой относительное распределение частот каждого возможного состояния. Больцманн математически утверждал, что эффект столкновений между частицами неизбежно приведёт к увеличению Н-функции от любой начальной конфигурации до достижения равновесия, и далее идентифицировал её как лежащее в основе микроскопического обоснования макроскопической термодинамической энтропии Клаузиуса.

Определение Больцмана вскоре было переработано Уиллардом Гиббсом в общую формулу статистико-механической энтропии, которая больше не требует идентичных и не взаимодействующих частиц, а основана на вероятностном распределении pi для всего микросостояния i общей системы:

Эта (Гиббсовская) энтропия, как можно показать на основе статистической механики, находится в прямом соответствии с классическим термодинамическим определением Клаузиуса.

Сам Шеннон, по-видимому, не был особенно осведомлен о близком сходстве между его новой мерой информации и предыдущей работой в области термодинамики, но Джон фон Нейман был. Говорят, что когда Шеннон решал, как назвать свою новую меру и боялся, что термин “информация” уже был чрезмерно загружен, фон Нейман твердо сказал ему: “Следует назвать новую меру энтропией, по двум причинам. Во-первых, соответствующая функция неопределённости использовалась в статистической механике под этим названием, поэтому у неё уже есть название. Во-вторых, что ещё более важно, никто не знает, что такое энтропия на самом деле, поэтому в дебатах вы всегда будете иметь преимущество”.

Информация – это одно из фундаментальных понятий современной науки, наряду с понятиями материи и энергии. По-видимому, не только понятие. В начале прошлого века Эйнштейн показал, что материя и энергия – по сути одно и то же (знаменитая формула \(E=m c^2\) ). Современные исследования в физике указывают на то, что подобная связь может быть и между информацией и энергией.

С точки зрения же человека, информация – это некие сведения, которые могут быть понятными, достоверными, актуальными и т.п., или наоборот.

Существуют различные формальные подходы к определению информации. С точки зрения информатики, нас интересуют два определения.

Информация по Шеннону Информация – это снятая неопределенность.

Это удобное интуитивное определение. Неопределенность в данном случае – характеристика нашего незнания о предмете. Например, в момент броска игрального кубика, мы не знаем, какая из 6 граней выпадет. Когда же кубик останавливается на какой-то грани – мы получаем информацию.

Это определение, однако, не слишком удобно без некоторой количественной меры неопределенности.

Величина неопределенности количество возможных равновероятных исходов события

Так, например, игральный кубик имеет неопределенность 6.

Такой подход к определению информации называется содержательным. Он интуитивно понятен, однако, не отвечает на вопрос “сколько информации получено”.

В качестве основной единицы количества информации принято брать бит – от binary digit.

При алфавитном подходе один бит – это количество информации, которое можно закодировать одним двоичным знаком (0 или 1). С точки зрения содержательного подхода, один бит – это количество информации, уменьшающее неопределенность в два раза.

Существуют более крупные единицы информации, которые чаще используются на практике.

название	размер
байт	8 бит
килобайт	\(10^3\) байт
мегабайт	\(10^6\) байт
гигабайт	\(10^9\) байт
терабайт	\(10^\) байт
кибибайт	\(2^\) байт
мебибайт	\(2^\) байт
гибибайт	\(2^\) байт
тебибайт	\(2^\) байт

В вопросе хранения информации, основным показателем является не количество информации, а информационный объем

В отличие от количества информации, информационный объем может быть не минимальным. В частности, кодирование текстов в различных кодировках далеко не оптимально.

Как уже говорилось, теория информации изучает количественные закономерности, связанные с получением, передачей, обработкой и хранением информации.

Одной из задач теории информации является отыскание наиболее экономных методов кодирования, позволяющих передать заданную информацию с помощью минимального количества символов. Эта задача решается как при отсутствии, так и при наличии помех в канале связи.

Другая типичная задача теории информации ставится следующим образом: имеется источник информации (передатчик), непрерывно вырабатывающий информацию, и канал связи, по которому эта информация передаётся в другую точку (на приёмник). Какова должна быть пропускная способность канала связи для того, чтобы канал “справлялся” со своей задачей, т. е. передавал всю поступающую информацию без задержек и искажений?

Ряд задач теории информации относится к определению объёма запоминающих устройств, предназначенных для хранения информации, к способам ввода информации в эти запоминающие устройства и вывода её для непосредственного использования.

Чтобы решать подобные задачи, нужно прежде всего научиться измерять количественно объем передаваемой или хранимой информации, пропускную способность каналов связи и их чувствительность к помехам (искажениям).

Читайте также: