Теорема о разложении вектора по трем некомпланарным векторам доказательство кратко

Обновлено: 05.07.2024

где x, y, и z - некоторые числа, то говорят, что вектор разложен по векторам , и . Числа x, y и z называются коэффициентами разложения.

Докажем теорему о разложении вектора по трем некомпланарным векторам.

Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

Пусть , и - данные некомпланарные вектора. Докажем сначала, что любой вектор р можно представить в виде . Затем докажем единственность коэффициентов разложения.

Доказательство: Пусть , и - данные некомпланарные вектора

Отметим произвольную точку О и отложим от нее векторы. Через точку Р проведем прямую параллельную ОС. Р1 точка пересечения прямой с плоскостью АОВ (если Р принадлежит ОС, то в качестве Р1 возьмем точку О). Через Р1 проведем прямую Р1Р2 параллельную ОВ; Р2 точка пересечения этой прямой с ОА (если Р1 принадлежит ОВ то в качестве Р2 возьмем точку О);

2) По правилу многоугольника

Заметим, что векторы ОР2 и ОА, Р2Р1 и ОВ. Р1Р и ОС коллинеарны. Значит, существуют такие числа x, y и z, что. Получаем, что

Существование разложения доказано.

Докажем единственность коэффициентов разложения. Допустим, что имеется ещё одно разложение вектора р;

Вычитая это равенство из ; получим

Это равенство выполняется только тогда, когда. Если предположить, например, что , то из этого равенства получим

Тогда, векторы , и – компланарны. Это противоречит условию теоремы.

Значит, наше предположение неверно, , Следовательно, коэффициенты разложения определяются единственным образом. Теорема доказана.

Дан параллелепипед АВСDA1B1C1D1.

Разложите вектор BD1 по векторам BA, ВС и ВВ1.

По правилу параллелепипеда вектор ВД1 равен сумме векторов ВА, ВС и ВВ1.

Решим эту же задачу под буквой б. Здесь нужно разложить вектор B1D1 по векторам А1A, А1В и А1D1.

По правилу треугольника из треугольника А1В1D1:

Вектор В1D1 равен сумме векторов B1A1+ А1D1 вектор В1A1 из А1В1B равен сумме .В1B + BA1 . Вектор ВВ1 = АА1. Вектор ВА1 = – А1В.

векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами .

три вектора называются компланарными , если они, будучи приведёнными к общему началу, лежат в одной плоскости.

Всегда возможно найти плоскость, параллельную двум произвольным векторам, поэтому любые два вектора всегда компланарные.

1. Любые два вектора находятся в одной плоскости, но в одной плоскости можно разместить и векторы AA 1 → , CC 1 → и AD → , то есть, эти векторы компланарны. Также компланарны векторы AA 1 → , AB → и CC 1 → , так как два из этих векторов параллельны. Легко представить, что если привести их к общему началу, то вектор CC 1 → совпадёт с вектором AA 1 → .

2. Например, векторы AB → , AD → и AA 1 → не компланарны, так как их нельзя разместить в одной и той же плоскости.

пусть векторы a → и b → не коллинеарны. Если для вектора c → существует единственная пара реальных чисел \(x\) и \(y\), такая, что c → = x ⋅ a → + y ⋅ b → , то векторы a → , b → и c → компланарны.

если три вектора a → , b → и c → компланарны и векторы a → и b → не коллинеарны, то вектор c → можно разложить по векторам a → и b → одним-единственным образом.

Если разложить вектор AC → по векторам AA 1 → и AA 2 → , то это можно сделать одним-единственным образом: AC → = AB → + AD → = x ⋅ AA 1 → + y ⋅ AA 2 → .

3. Диагональ параллелепипеда, которая выходит из этой же точки, изображает суммы векторов AB → , AD → и AA 1 → .

Теорема о разложении по базису в пространстве
Любой вектор d → можно разложить по трём данным некомпланарным векторам a → , b → и c → , причём реальные коэффициенты разложения \(x\), \(y\) и \(z\) определяются единственным образом: A C 1 → = AD → + AB → + A A 1 → = x ⋅ AA 2 → + y ⋅ AA 3 → + z ⋅ AA 4 → .

Теорема. Любой вектор m может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых некомпланарных векторов а, b и с:

m = xa + yb + zc. (1)

Прежде всего отметим, что никакие два вектора из векторов а, b, с не коллинеарны; в противном случае векторы а, b, с были бы компланарны. Поэтому, если вектор m компланарен с какими-нибудь двумя векторами (например, с а и b), то m = ха + уb и, следовательно,

m = ха + уb + 0 • с,

т. е. в этом случае теорема доказана.

Пусть вектор m не компланарен ни с какими двумя векторами из векторов а, b, с (рис. 30).

Приведем все векторы к общему началу О и проведем через точку М (конец направленного отрезка, изображающего вектор \(\overrightarrow\) = т) прямую, параллельную вектору с. Эта прямая пересечет плоскость ОАВ в некоторой точке N. Ясно, что

\(\overrightarrow\) = \(\overrightarrow\) + \(\overrightarrow\).

По свойству коллинеарных векторов \(\overrightarrow\) = zc.

По теореме о разложении вектора по двум неколлинеарным векторам существуют числа х, у такие, что \(\overrightarrow\) = ха + уb.

\(\overrightarrow\) = \(\overrightarrow\) + \(\overrightarrow\) = xa + yb + zc.

Единственность разложения вектора т по векторам а, b и с: доказывается аналогично тому, как это было сделано в теореме о разложении вектора по двум неколлинеарным векторам.

Базисом пространства называются любые три некомпланарных вектора, взятые в определенном порядке.

Пусть e₁, e₂ и e₃ - некоторый базис, и a - произвольный вектор. Тогда, по только что доказанной теореме, существуют три числа х, у, z таких, что

а = хe₁ + уe₂ + ze₃.

Числа х, у и z называются координатами вектора а в данном базисе. В этом случае пишут а = (х; у; z).

Задача 1. Дан куб ABCDA₁B₁C₁D₁. Разложить вектор \(\overrightarrow\), где K - центр грани ВСС₁В₁ по векторам а = \(\overrightarrow\), b = \(\overrightarrow\), с = \(\overrightarrow\) (рис. 31).

Из \(\Delta\)AKL имеем \(\overrightarrow\) = \(\overrightarrow\) + \(\overrightarrow\), но

Задача 2. Пусть векторы \(\overrightarrow\), \(\overrightarrow\), \(\overrightarrow\), изображенные соответствующими направленными ребрами треугольной пирамиды ABCD, образуют базис. Найти координаты вектора \(\overrightarrow\) в этом базисе.

Воспользуемся рис. 29a.

Обозначив \(\overrightarrow\) = e₁, \(\overrightarrow\) = e₂, \(\overrightarrow\) = e₃, получим \(\overrightarrow\) = \(\overrightarrow\) - \(\overrightarrow\) = - e₁ + e₂ или \(\overrightarrow\) = - 1•e₁ + 1•e₂ + 0•e₃,

В ходе этого урока учащиеся узнают, что любой вектор пространства можно разложить по трём некомпланарным векторам. При решении задач они приобретут навык такого разложения и смогут без труда определять его коэффициенты.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Разложение вектора по трем некомпланарным векторам"

Аналогично тому, как на плоскости любой вектор можно разложить по двум неколлинеарным векторам, наверняка, в пространстве любой вектор можно разложить по трём некомпланарным векторам.

Говорят, что вектор разложен по векторам , , если он представлен в виде суммы произведений вектора на число x, вектора на число y и вектора на число z.

При этом числа x, y и z называют коэффициентами разложения.

Запишем теорему. Любой вектор можно разложить по трём некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

Докажем эту теорему для некомпланарных векторов , , .

Отметим любую удобную точку пространства и отложим от неё векторы , , и равные векторам , , соответственно.

Далее через точку P проведём прямую параллельную прямой OC. Точку пересечения этой прямой с плоскостью ABC обозначим за P₁.

Далее через точку P₁ проведём прямую параллельную прямой OB. А точку пересечения этой прямой с прямой ОА обозначим за P₂.

Пользуясь правилом многоугольника сложения нескольких векторов, запишем, что .

Из построений следует, . А это значит, что .

Таким образом мы разложили вектор по трём некомпланарным векторам , , .

Осталось только доказать, что коэффициенты разложения x, y, z определяются единственным образом.

Допустим, что кроме полученного нами разложения есть ещё одно, в котором коэффициенты разложения равны x₁, y₁, z₁.

Вычтем второе разложение из первого.

Понятно, что в разложении нулевого вектора по трём некомпланарным ненулевым векторам все коэффициенты разложения должны быть равны нулю.

Отсюда соответственно равны коэффициенты:

А это противоречит нашему допущению о том, что коэффициенты второго разложения вектора отличны от коэффициентов первого разложения.

Отсюда получаем, что коэффициенты разложения x, y, z определяются единственным образом.

Что и требовалось доказать.

Выполним несколько заданий.

Задача. параллелепипед.

а) вектор по векторам , и ;

б) вектор по векторам , и .

Изобразим все векторы, перечисленные в первом пункте. Пользуясь правилом параллелепипеда сложения трёх некомпланарных векторов, нетрудно заметить, что . Таким образом мы разложили вектор по данным векторам. Причём каждый коэффициент данного разложения равен единице.

Обратимся к следующему пункту. Вектор нужно разложить по векторам , и .

Для начала запишем, что по правилу многоугольника сложения нескольких векторов, вектор .

Так мы разложили вектор по данным векторам, где коэффициенты разложения y и x равны 1, а z равно -1.

Задача. параллелепипед. точка пересечения диагоналей. Разложить векторы и по векторам , и .

Сразу можно отметить, что .

Поэтому в разложении этого вектора по данным векторам коэффициенты разложения при векторах и равны 0, а при векторе — -1.

Далее разложим вектор по данным векторам.

Задача. тетраэдр. середина ребра . Разложить векторы по векторам , и . Если , и .

Для начала стоит отметить, что на рёбрах DC и DB тетраэдра можно построить параллелограмм. И отрезок DK будет являться половиной его диагонали DD₁. Действительно, точка К является серединой второй диагонали BC, а значит, она является точкой пересечения диагоналей данного параллелограмма.

Рассмотрим каждый вектор этой суммы в отдельности.

Подставим полученные суммы в выражение для вектора .

Подведём итоги этого урока.

На нём вы узнали, что аналогично тому, как на плоскости любой вектор можно разложить по двум неколлинеарным векторам, в пространстве любой вектор можно разложить по трём некомпланарным векторам.

Говорят, что вектор разложен по векторам , и , если он представлен в виде суммы произведений вектора на число x, вектора на число y и вектора на число z. При этом числа x, y, z называют коэффициентами разложения.

Также мы доказали, что любой вектор можно разложить по трём некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

Любой вектор в пространстве можно разложить по трем заданным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

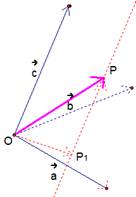
Рис. 5. Разложение вектора по трем некомпланарным

Дано: некомпланарные векторы и , произвольный вектор .

Построим все заданные векторы из одной точки – точки О (рис. 5). Рассмотрим плоскость, образованную векторами и . Из точки Р проведем прямую , параллельно направлению . – точка пересечения плоскости и прямой. Векторы и по построению коллинеарны, значит имеем: . Теперь, согласно правилу треугольника, имеем: . Вектор мы нашли. Вектор , согласно построению, лежит в плоскости векторов и , значит, согласно теореме, рассмотренной выше, о разложении вектора через два неколлинеарных имеем: .

Так, получено разложение произвольного вектора в пространстве через три некомпланарных вектора:

Докажем, что такое разложение единственно. Используем метод от противного. Предположим, что есть еще тройка чисел ( ), с помощью которой можно заданный вектор разложить по трем некомпланарным. . Имеем систему:

Вычтем из первого уравнения второе:

Получить нулевой вектор из трех некомпланарных ненулевых векторов путем их сложения можно только в случае, когда: , , .

Так, доказано, что возможно единственное разложение вектора по трем некомпланарным.

Домашнее задание