Представление синусоидальных величин комплексными числами кратко

Обновлено: 05.07.2024

Метод расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, называется методом комплексных величин, методом комплексных амплитуд или комплексным методом расчета.

Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

показательной

тригонометрической или

алгебраической - формах.

Пусть мгновенная ЭДС задаётся уравнением:

. На комплексной плоскости вращающийся вектор:

Мнимая составляющая комплексного числа вектора на комплексной плоскости определяет синусоидальное изменение ЭДС и обозначается символом Im.

. Комплексное число удобно представить в виде произведения двух комплексных чисел

. Комплексное число Ė_m, соответствующее положению вектора в начальный момент времени называют комплексной амплитудой:

. Комплексное число e j∙ω∙t является оператором поворота вектора на угол ω∙t относительно начального положения вектора.

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака ? произведения комплекса амплитуды Ė_m и оператора вращения e j∙ω∙t :

. Переход от одной формы записи, к другой, осуществляется с помощью формулы Эйлера: , где

- показательная (полярная) форма,

- тригонометрическая. Чтобы преобразовать в показательную:

Применение комплексных чисел позволяет от геометрического сложения или вычитания векторов на векторной диаграмме перейти к алгебраическому действию над комплексными числами этих векторов.

Если гармонически изменяющаяся величина представлена в виде косинусоидальной функции времени:

то её мгновенное значение равно действительной части произведения комплексной амплитуды и оператора вращения.

2) Любое комплексное число может быть представлено как формальная сумма , где и — вещественные числа, — мнимая единица

На комплексной плоскости вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.

3) Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени с комплексными коэффициентами имеет ровно комплексных корней. Это одна из главных причин широкого применения комплексных чисел в научных исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках —электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.

4) Модулем комплексного числа называется – длина вектора, изображающего комплексное число. Модуль комплексного числа обозначается , а также буквой r.

r= Угол между осью абцисс и вектором ОМ, изображающим комплексное число , называется аргументом комплексного числа Каждое неравное нулю комплексное число имеет бесконечное множество аргументов, отличающихся друг от друга на целое число полных оборотов.

Резонанс токов

Рассмотрим теперь случай, когда у параллельно соединенных конденсатора и катушки оказались равными их реактивные сопротивления, т. е. XlL = XC.

Если мы, как и прежде, будем считать, что катушка и конденсатор не обладают активным сопротивлением, то при равенстве их реактивных сопротивлений (YL = YC) общий ток в неразветвленной части цепи окажется равным нулю, тогда как в ветвях будут протекать равные токи наибольшей величины. В цепи в этом случае наступает явление резонанса токов.

При резонансе токов действующие значения токов в каждом разветвлении, определяемые отношениями IL = U / XL и IC = U / XC будут равны между собой, так XL = ХC.

При резонансе токов, как и при резонансе напряжений, происходит колебание энергии между полем катушки и полем конденсатора. Генератор, сообщив однажды энергию цепи, оказывается как бы изолированным.

Значения L, С и f, при которых наступает резонанс токов, определяются, как и при резонансе напряжений (если пренебречь активным сопротивлением контура), из равенства:

ωL = 1 / ωC Следовательно: fрез = 1 / 2π√LC , Lрез = 1 / ω 2 С, Срез = 1 / ω 2 L

Изменяя любую из этих трех величин, можно добиться равенства Xl = Xc, т. е. превратить цепь в колебательный контур.

Итак, мы получили замкнутый колебательный контур, в котором можно вызвать электрические колебания, т. е. переменный ток. И если бы не активное сопротивление, которым обладает всякий колебательный контур, в нем непрерывно мог бы существовать переменный ток. Наличие же активного сопротивления приводит к тому, что колебания в контуре постепенно затухают и, чтобы поддержать их, необходим источник энергии - генератор переменного тока.

В цепях несинусоидального тока резонансные режимы возможны для различных гармоничных составляющих. Угловая частота w₀, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

Билет №23.

1.1)Алгебраическая форма Запись комплексного числа в виде называется алгебраической формой комплексного числа.

Тригонометрическая форма

Если вещественную и мнимую части комплексного числа выразить через модуль и аргумент ( , ), то комплексное число можно записать в тригонометрической форме

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем

Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01 ¸ 10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i - мгновенное значение тока ;

u – мгновенное значение напряжения ;

е - мгновенное значение ЭДС ;

р - мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ) .

Действующее значение переменного тока

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂ соответствуют уравнения:

Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени ( t =0): и - начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂ угол сдвига фаз:

Векторное изображение синусоидально
изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени ( t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.

На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Представление синусоидальных ЭДС, напряжений
и токов комплексными числами

показательной

тригонометрической или

алгебраической - формах.

Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число

Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

Комплексное число удобно представить в виде произведения двух комплексных чисел:

Параметр , соответствующий положению вектора для t =0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой: , а параметр - комплексом мгновенного значения.

Параметр является оператором поворота вектора на угол w t относительно начального положения вектора.

Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ± a .

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды и оператора поворота :

Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:

Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

- то для записи ее в показательной форме, необходимо найти начальную фазу , т.е. угол, который образует вектор с положительной полуосью +1:

Тогда мгновенное значение напряжения:

При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)

а при (третий квадрант)

Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:

Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.

Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:

Действующее значение синусоидальных ЭДС, напряжений и токов

В соответствии с выражением (3) для действующего значения синусоидального тока запишем:

Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:

Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения

1. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?

2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?

3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?

4. Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.

Синусоидальные ЭДС, напряжения и токи можно изображать графически в виде соответствующих синусоид, такие графики в электротехнике называют волновыми диаграммами (см. рис. 13).

Обычно на одной волновой диаграмме изображают несколько синусоид переменных величин (напряжений, токов), относящихся к одной и той же цепи. Для оценки их взаимного расположения вдоль оси абсцисс вводится разность их начальных фаз, называемая фазовым сдвигом. Чаще всего встречается фазовый сдвиг между током и напряжением.

Если фи>0 , то говорят, что напряжение опережает ток по фазе, при фи напряжение отстает по фазе от тока, при фи=0 напряжение и ток совпадают по фазе, а если фи=П , то напряжение и ток находятся в противофазе.

Волновые диаграммы не всегда удобны для исследования, особенно при сложных разветвленных цепях. Проще в этом случае изображать синусоидальные величины вращающимися векторами. Изобразим вращающийся вектор, соответствующий току:

Длина отрезка ОА в принятом масштабе равна амплитуде тока . Проекция вектора на ось ординат (ОВ) равна мгновенному значению тока в момент времени . При вращении вектора в положительном направлении (т.е. против часовой стрелки) с угловой скоростью в любой момент времени его проекция на ось ординат будет равна соответствующему мгновенному значению тока:

Любой вектор на плоскости, проведенный из начала координат и изображающий значение ЭДС, напряжения или тока, однозначно определяется точкой, соответствующей концу этого вектора (точка на рисунке).

Комплексное число (соответствующее точке ) имеет вещественную (ОС) и мнимую (ОВ) составляющие на комплексной плоскости.

Перевод комплексных чисел из одной формы в другую можно производить по следующим формулам:

Для напряжения и тока аналогично.

При расчетах цепей синусоидального тока целесообразно перейти от гармонических функций времени к их изображениям в комплексной форме и производить все расчеты, используя комплексные числа. Конечный результат может быть представлен снова в виде синусоидальной функции времени.

Это значение тока иногда называют средневыпрямленным.

1.4.2. Формы представления синусоидальных величин

Представление синусоидальных величин проекциями вращающегося вектора

Синусоидальные величины, имеющие угловую частоту ω, можно изображать векторами, вращающимися с угловой скоростью ω, причем длина вектора в соответствующем масштабе определяется амплитудой тока (э.д.с, напряжения). В отличие от механики эти векторы не означают направления действия величины!

Для представления тока построим из начала координат радиус вектор, модуль которого равен амплитуде тока, под углом к горизонтальной оси X. Будем обозначать такой вектор I_m, U_m, E_m. (рис.1.36)

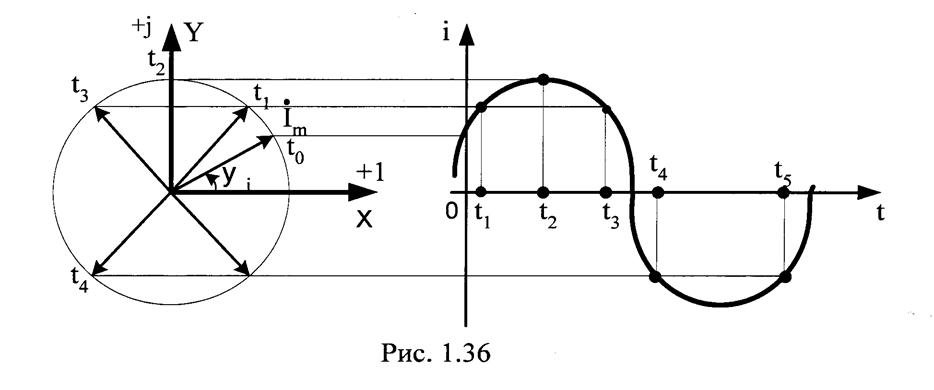Значение проекции вектора на вертикальную ось - I_msinψ_i - значение тока в момент t = 0.

Приведем вектор во вращение против часовой стрелки с угловой скоростью ω. Полный оборот совершается за время, равное Т.

В этом случае проекция вращающегося вектора на вертикальную ось равна в избранном масштабе мгновенному значению тока -

Рядом с окружностью, описываемой концом вектора можно построить развернутую диаграмму (рис. 1.36).

Использование векторов особенно наглядно, если необходимо изобразить несколько синусоидальных величин с разными начальными фазами. Если все величины имеют одинаковую частоту ω, то важны только амплитуды и сдвиг фаз между величинами. Вращение радиусов векторов можно не изображать.

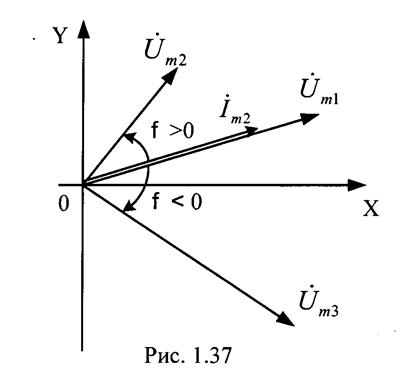
Совокупность неподвижных векторов изображающих синусоидальные токи, э.д.с, напряжения одной частоты в начальный момент времени называется векторной диаграммой.

Сдвиг фаз между током и напряжением φ=ψ_u – ψ_i

Если φ >0, то напряжение опережает по фазе ток (ток отстает от напряжения).

Читайте также: