Поясните цель приведения силы к точке кратко
Обновлено: 30.06.2024
Ранее мы установили, что вектор силы можно переносить по линии действия в любую точку тела.
Попробуем силу (рис. 5.1) перенести в какую-нибудь точку , не расположенную на линии действия.

Приложим к этой точке две уравновешивающиеся силы и , параллельные силе и равные ей по величине, .
В результате получим силу равную силе и приложенную к точке . То есть мы как бы перенесли заданную силу из точки в точку , но при этом появилась пара, образованная силами и . Момент этой пары

равен моменту заданной силы относительно точки .
Процесс замены силы равной ей силой приложенной к точке , и парой называется приведением этой силы к точке .
Точка называется точкой приведения; сила приложенная к точке приведения, — приведенной силой. Появившаяся пара — присоединенной парой.
- Сложение сил, произвольно расположенных в пространстве

Пусть дана система, состоящая из нескольких произвольно расположенных сил (на рис. 5.2 показаны три силы ). Требуется сложить эти силы и посмотреть, что в результате получится.

Приведем все силы к произвольно выбранной точке , центру приведения. Получим систему приведенных сил, приложенных к точке , равных заданным силам: , и систему присоединенных пар, моменты которых равны векторам моментов заданных сил относительно центра приведения :


Сложив первую систему, систему сходящихся приведенных сил, например, построением многоугольника сил , получим их равнодействующую которая равна векторной сумме этих приведенных сил, а значит, и заданных сил, потому что они векторно равны

А сложив систему пар, например, построением многоугольника их векторов моментов , получим пару, момент которой равен векторной сумме моментов присоединенных пар или сумме моментов заданных сил относительно центра приведения


Сила равная векторной сумме заданных сил, называется главным вектором этих сил. Приложена эта сила к центру приведения.

Момент равный векторной сумме моментов заданных сил относительно центра приведения, называется главным моментом этих сил относительно центра приведения.

Главный вектор можно найти так же, как находили ранее равнодействующую сходящихся сил (см. И, §2, формула (2.2)).
Проекции его на оси (см. рис. 5.2)

Поэтому модуль главного вектора


Направление вектора определяется с помощью направляющих косинусов:

где — углы между вектором и направлением осей

Так как векторы моментов присоединенных пар также образуют систему сходящихся векторов, то и главный момент находим аналогичным способом

где — проекции вектора на оси. Проектируя его на оси, получим, принимая во внимание, что проекция вектора момента силы относительно точки на ось, проходящую через эту точку, есть момент относительно оси (3.4):

Эти проекции — вектора главного момента на оси, равные алгебраическим суммам моментов заданных сил относительно осей, проходящих через центр приведения, называются главными моментами сил относительно соответствующих осей.

Модуль главного момента находится по (5.4) или с учетом (5.5)

Направление этого вектора можно найти с помощью направляющих косинусов

где — углы между и направлением осей
Итак, при сложении сил, произвольно расположенных в пространстве, в общем случае получается сила , приложенная к центру приведения, и пара с моментом .
Два важных замечания. Первое — главный вектор не является равнодействующей заданных сил, так как он не может один заменить действие всех сил, а только вместе с парой.
Второе — главный вектор как векторная сумма заданных сил не зависит от положения центра приведения. А главный момент зависит, так как моменты заданных сил относительно центра приведения изменятся, если этот центр будет в другом месте.
Конечно, возможны различные результаты сложения сил.

Это значит, что в результате сложения получится только сила, равная главному вектору. И она, эта сила, в данном частном случае является равнодействующей всей системы сил. Линия действия равнодействующей будет проходить через этот центр приведения.
В этом частном случае имеет место очень важная и полезная теорема — теорема Вариньона.
Пусть на тело действует несколько сил и у них существует равнодействующая , приложенная к центру приведения (рис. 5.3).

Покажем радиусы-векторы, проведенные из некоторой точки — радиус-вектор точки приложения равнодействующей; — точек , точек приложения сил , где . И добавим векторы , соединяющие точку сточками .
Момент сил относительно точки :



Сумма моментов всех действующих сил относительно точки





равна главному моменту сил относительно точки , который в этом частном случае равен нулю. Поэтому


Если у системы сил имеется равнодействующая, то момент равнодействующей относительно любой точки равен векторной сумме моментов всех сил относительно этой точки

Следствие. Если спроектировать это векторное равенство на какую-нибудь ось, например , проходящую через точку , то, имея в виду доказанный ранее результат (3.4), получим теорему Вариньона в другой форме.
Если у системы сил имеется равнодействующая, то момент ее относительно любой оси равен алгебраической сумме моментов всех сил относительно этой оси

А так как момент пары сил относительно любой точки равен моменту этой пары (IV, §2), то в этом случае, когда , главный момент не зависит от выбора центра приведения. Относительно любой точки он будет одинаков и равен

И, наконец, может оказаться, что и главный вектор и главный момент равны нулю. В этом случае силы уравновешиваются, а тело под действием этих сил находится в равновесии.

и главный момент

то для равновесия тела необходимо выполнение шести условий

Эти условия называются уравнениями равновесия сил, произвольно расположенных в пространстве.
В частности, если силы расположены в одной плоскости, то, направив оси так, чтобы ось стала перпендикулярна этой плоскости, третье уравнение , четвертое и пятое обратятся в тождества, а в шестом — моменты сил относительно оси будут равны моментам относительно точки , точки пересечения оси и плоскости.
Останутся только три уравнения из шести:

Так как в системе уравнений (5.10) уравнения моментов удовлетворяются относительно любой оси, то таких уравнений моментов можно составить больше трех, хоть все шесть.
Точно так же в системе уравнений (5.11) для плоской системы сил можно составить и два, и три уравнения моментов. Поэтому возможны три варианта

Правда, имеются ограничения на выбор точек и осей. Например, при использовании II варианта точки и не должны лежать на прямой, перпендикулярной оси; а в III варианте — точки и не должны располагаться на одной прямой.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Кстати возможно вам будут полезны эти страницы:





















































Образовательный сайт для студентов и школьников
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Силу можно перенести параллельно линии ее действия, при этом нужно добавить пару сил с моментом, равным произведению модуля силы на расстояние, на которое перенесена сила.

Дано: сила в точке А (рис. 5.1).
Добавим в точке В уравновешенную систему сил ( F 1 ; F "). Образуется пара сил ( F ; F "). Получим силу в точке В и момент пары т.
Приведение к точке плоской системы
произвольно расположенных сил
Линии действия произвольной системы сил не пересекаются в одной точке, поэтому для оценки состояния тела такую систему следует упростить
Тема 1.4. Плоская система произвольно расположенных сил 35
Для этого все силы системы переносят в одну произвольно выбранную точку — точку приведения. Применяют теорему Пуансо. При любом переносе силы в точку, не лежащую на линии ее действия, добавляют пару сил.
Появившиеся при переносе пары называют присоединенными парами.
Дана плоская система произвольно расположенных сил (рис. 5.2).
Переносим все силы в точку О. Получим пучок сил в точке О, который можно заменить одной силой — главным вектором системы. Образующуюся систему пар сил можно заменить одной эквивалентной парой — главным моментом системы.

Главный вектор равен геометрической сумме векторов произвольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.

По величине проекций главного вектора на оси координат находим модуль главного вектора:

Главный момент системы сил равен алгебраической сумме моментов сил системы относительно точки приведения.
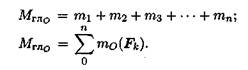
Таким образом, произвольная плоская система сил приводится к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).
Влияние точки приведения
Точка приведения выбрана произвольно. При изменении положения точки приведения величина главного вектора не изменится.
Величина главного момента при переносе точки приведения изменится, т. к. меняются расстояния от векторов-сил до новой точки приведения.
С помощью теоремы Вариньона о моменте равнодействующей можно определить точку на плоскости, относительно которой главный момент равен нулю. Тогда произвольная плоская система сил может быть заменена одной силой.
Эту силу называют равнодействующей системы сил.
Численно равнодействующая равна главному вектору системы сил, но приложена в другой точке, относительно которой главный момент равен нулю. Равнодействующую принято обозначать F Σ .
Численно ее значение определяется так же, как главный вектор системы сил:

Точку приложения равнодействующей можно определить по формуле

где d — расстояние от выбранной точки приведения до точки приложения равнодействующей;
Тема 1.4. Плоская система произвольно расположенных сил 37
Мгл — величина главного момента относительно выбранной точки приведения;
F гл — величина главного вектора системы сил.
Частные случаи приведения системы сил к точке
При приведении системы сил к точке возможны следующие варианты:

© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.004)
Рассмотрим случай переноса силы в произвольную точку,не лежащую на линии действия силы.

Возьмем силу F, приложенную в точке С. Требуется перенести эту силу параллельно самой себе в некоторую точку О. Приложимв точке О две силы F' и F", противоположно направленные, равные по значению и параллельные заданной силе F, т. е. F' = F" = F. От приложения в точке О этих сил состояние тела не изменяется, так как они взаимно уравновешиваются. Полученную систему трех сил можно рассматривать как состоящую из силы F', приложенной в точке О, и пары сил FF" с моментом М = Fa. Эту пару сил называют присоединенной, а ее плечо а равно плечу силы F относительно точки О.

Таким образом, при приведении силы F к точке, не лежащей на линии действия силы, получается эквивалентная система, состоящая из силы, такой же по модулю и направлению, как и сила F, и присоединенной пары сил, момент которой равен моменту данной силы относительно точки приведения:

В качестве примера приведения силы рассмотрим действие силы F на конец С защемленного стержня (рис.28,б). После приведения силы F в точку О защемленного сечения обнаруживаем в нем силу F1 равную и параллельную заданной, и присоединенный момент М, равный моменту заданной силы F относительно точки приведения О,
1.4.2 Приведение плоской системы сил к данной точке
Описанный метод приведения одной силы к данной точке можно применить к какому угодно числу сил. Допустим, что в точках тела А, В, С и D (рис. 30) приложены силы F1,F2,F3,F4.
Требуется привести эти силы к точке О плоскости. Приведем сначала силу F1 , приложенную в точке А. Приложим в точке О две силы F1' и F1'', параллельные ей и направленные в противоположные стороны. В результате приведения силы F1 получим силу F1' , приложенную в точке О, и пару сил F1' F1'' с плечом a1. Поступив таким же образом с силой F2 , приложенной в точке В, получим силу F2', приложенную в точке О, и пару сил с плечом a2 т. д.

Плоскую систему сил, приложенных в точках А, В, С и D, мы заменили сходящимися силами F1,F2,F3,F4 , приложенными в точке О, и парами сил с моментами, равными моментам заданных сил относительно точки О:

Сходящиеся в точке силы можно заменить одной силой F'гл, равной геометрической сумме составляющих,
Эту силу, равную геометрической сумме заданных сил, называют главным вектором системы сил и обозначают F'гл .

На основании правила сложения пар сил их можно заменить результирующей парой, момент которой равен алгебраической сумме моментов заданных сил относительно точки О и называется главным моментом относительно точки приведения
Следовательно, в общем случае плоская система сил в результате приведения к данной точке О заменяется эквивалентной ей системой, состоящей из одной силы (главного вектора) и одной пары (главного момента).
Необходимо усвоить, что главный вектор F'гл является равнодействующей данной системы сил, так как эта система не эквивалентна одной силе F'гл. Только в частном случае, когда главный момент обращается в нуль, главный вектор будет равнодействующей данной системы сил. Так как главный вектор равен геометрической сумме сил заданной системы, то ни модуль, ни направление его не зависят от выбора центра приведения. Значение и знак главного момента Mгл зависят от положения центра приведения, так как плечи составляющих пар зависят от взаимного положения сил и точки (центра), относительно которой берутся моменты.
Могут встретиться следующие случаи приведения системы сил: 1. — общий случай; система приводится главному вектору и к главному моменту. 2. ; система приводится к одной равнодействующей, равной главному вектору системы. 3. ; система приводится к паре сил, момент которой равен главному моменту. 4. ; система находится в равновесии, т. е. для равновесия плоской системы сил необходимо и достаточно, чтобы ее главный вектор и главный момент одновременно были равны нулю.
Можно доказать, что в общем случае, когда , всегда есть точка, относительно которой главный момент сил равен нулю.
Рассмотрим плоскую систему сил, которая приведена к точке О, т. е. заменена главным вектором , приложенным в точке О, и главным моментом . Для определенности примем, что главный момент направлен по часовой стрелке, т. е. . Изобразим этот главный момент парой сил FF", модуль которых выберем равным модулю главного вектора , т. е. . Одну из сил, составляющих пару, приложим в центре приведения О, другую силу в точке С, положение которой определится из условия: . Следовательно .
Расположим пару сил так, чтобы сила F'' была направлена в сторону, противоположную главному вектору F'гл. В точке О имеем две равные взаимнопротивоположные силы F'гл и F'', направленные по одной прямой; их можно отбросить (согласно третьей аксиоме). Следовательно, относительно точки С главный момент рассматриваемой системы сил равен нулю, и система приводится к равнодействующей .
Не изменяя кинематического состояния твердого тела, силу, приложенную к нему в какой-либо точке, можно переносить параллельно ей самой в любую другую точку тела, прибавляя при этом пару с моментом M , равным моменту переносимой силы относительно точки, в которую переносится сила.
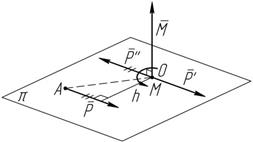
Пусть в точке A приложена сила P (рисунок 5.1). В произвольную точку O приложим уравновешенные силы P¢ и
P¢¢ , причем P
= P¢ = P ¢
действия сил параллельны. Тогда получим силу P¢ и пару сил (P, P¢¢),
момент которой равен моменту силы P относительно точки O :
M O (P )= r ´ P ; M O (P )= OA´ P ; M O (P )= Ph .
Приведение системы сил к данному центру
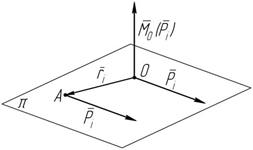
Приведем систему n сил к центру O (рисунок 5.2), для этого, на основании леммы Пуансо, перенесем каждую силу
P i в центр O , добавляя при этом пары
сил, моменты которых равны:
M O (P i )= r i ´ P i .
В результате приведения к центру O получим сходящуюся систему
сил, которую можно заменить главным вектором R* и получим n число
* системы сил, относительно центра O
M * = åM
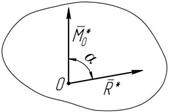
Любую систему сил, действующую на абсолютно твердое тело, можно привести к
одному центру и заменить одной силой R*
* (главный момент системы сил).
R* и главный момент
Хотя, по записи, главный вектор и равнодействующая одинаковы, необходимо различать эти два понятия.
1. Главный вектор не зависит от центра приведения.
2. Главный момент зависит от центра приведения, так как от его положения зависят величина и направление радиус-вектора.
3. Главный вектор заменяет систему сил только в совокупности с главным моментом, т.е. он не эквивалентен данной системе сил.
4. Равнодействующая может быть только у сходящейся системы сил
* = 0 , то данная система сил
5. Равнодействующая имеет определенную линию действия.
6. Равнодействующая одна заменяет сходящуюся систему сил, т.е. она эквивалентна ей.
Для того чтобы система сил находилась в равновесии необходимо и
R* и главный момент
Пример приведения системы сил к заданному центру O .
Пусть на твердое тело действует пространственная произвольная
система сил (Р1, Р2 . Р n )
(рисунок 5.4 а).
Приведем данную систему сил к заданному центру O (центр приведения), используя теорему Пуансо о параллельном переносе силы.
В результате приведения получим систему сходящихся сил
(Р1¢, Р2¢. Р n¢ ) и систему векторов моментов (M1, M2 . M n ), исходящих из
центра O (рисунок 5.4 б). По величине моменты будут соответственно равны:
M1 = P1b ;
M2 = P2a ;
M n = P n a .

P n¢ можно заменить одним вектором, –
главным вектором R* системы сил (рисунок 5.5 а), – равным их
R* = P¢+ P¢ + . + P¢.
Так как P1¢= P1 , P2¢ = P2 ,
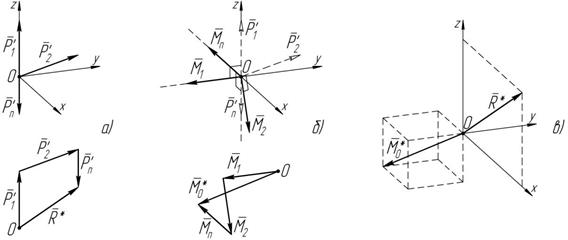
M n можно заменить одним вектором,
* системы сил (рисунок 5.5 б), – равным их
Возможные случаи приведения сил
При приведении сил, произвольно расположенных в пространстве, к заданному центру O возможны следующие случаи.
* парой сил (R* , R )
(рисунок 5.6 б), причем
M * = R*d или M * = R*d .
 |
R*
Случаи I – IV возможны при расположении сил в одной плоскости.
6 АНАЛИТИЧЕСКИЕ УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМ СИЛ
1. Равновесие пространственной произвольной системы сил, т.е. системы сил, линии действия которых произвольно расположены в пространстве (рисунок 6.1).
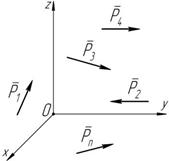 Рисунок 6.1 | å P ix = 0; åM x (P i ) = 0; å P iy = 0; åM y (P i ) = 0; å P iz = 0; åM z (P i ) = 0. |
Для равновесия пространственной произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси ( x , y , z ) и суммы моментов всех сил относительно
этих осей равнялись нулю.
Примечание. Оси, относительно которых составляются уравнения, не должны лежать в одной плоскости и быть параллельны.
2. Равновесие пространственной параллельной системы сил, т.е. системы сил расположенных в пространстве, линии действия которых параллельны (рисунок 6.2).
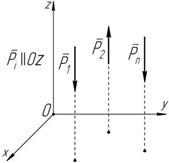 Рисунок 6.2 | Пусть линии действия всех сил параллельны оси Oz , тогда: å P iz = 0; åM x (P i ) = 0; åM y (P i ) = 0. |
Для равновесия пространственной параллельной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на ось параллельную линиям действия сил (ось Oz ) равнялась нулю, и суммы моментов всех сил относительно двух оставшихся осей ( x , y ) также
равнялись нулю.
3. Равновесие сходящихся систем сил, т.е. систем сил, линии действия которых пересекаются в одной точке (рисунки 6.3 и 6.4).
Пространственная сходящаяся
Плоская сходящаяся
Для равновесия пространственной сходящейся системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси ( x , y , z ) равнялись нулю.
Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы суммы проекций всех сил на две координатные оси ( x , y или x , z или y , z ) равнялись нулю.
4. Равновесие плоской произвольной системы сил, т.е. системы сил произвольно расположенных на плоскости (рисунок 6.5).
Существует III вида (формы) условий равновесия плоской произвольной системы сил.
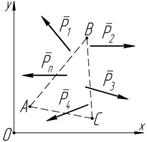 Рисунок 6.5 | Первый вид (основной): å P ix = 0; å P iy = 0; åM O (P i ) = 0. | Второй вид: å P ix = 0; åM A (P i ) = 0; åM B (P i ) = 0, прямая AB ^ Ox . | Третий вид: åM A (P i ) = 0; åM B (P i ) = 0; åM C (P i ) = 0, точки A , B и C Ï одной прямой. |
I. Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на две оси, лежащие в плоскости действия системы сил, равнялись нулю, и сумма моментов относительно любой точки (например точки O ), принадлежащей данной плоскости, также равнялась нулю.
II. Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на любую ось, принадлежащую плоскости действия системы сил (например ось Ox ), равнялась нулю, и суммы моментов всех сил относительно двух любых точек, принадлежащих данной плоскости (например точки A и B ), также равнялись нулю.
Примечание. Прямая AB не должна быть перпендикулярна оси Ox .
III. Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно трех произвольных точек, принадлежащих плоскости действия системы сил (например точек A , B и C ), равнялись нулю.
Примечание. Точки A , B и C не должны лежать на одной прямой.
5. Равновесие плоской параллельной системы сил, т.е. системы сил расположенных на плоскости, линии действия которых параллельны (рисунок 6.6).
Существуют II вида (формы) условий равновесия плоской параллельной системы сил.
Пусть линии действия всех сил параллельны оси Oy .
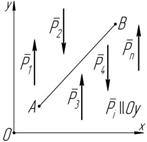 Рисунок 6.6 | Первый вид (основной): åP i y = 0; åM O (P i )= 0. | Второй вид: åM A (P i )= 0; åM B (P i )= 0, прямая AB Oy . |
I. Для равновесия плоской параллельной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную линиям действия сил (например Oy ), равнялась нулю, и сумма моментов всех сил
относительно какой-либо точки, принадлежащей плоскости действия системы сил (например точки O ), также равнялась нулю.
II. Для равновесия плоской параллельной системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно двух произвольных точек, принадлежащих плоскости действия системы сил (например точек A и B ), равнялись нулю.
Примечание. Точки A и B не должны лежать на прямой параллель- ной линиям действия сил.
ФЕРМА
Ферма – это шарнирно-стержневая, геометрически неизменяемая конструкция. Фермы бывают плоские и пространственные.
Ферма состоит из стержней (обозначенных цифрами) и узлов (обозначенных буквами). Рассмотрим плоскую ферму (рисунок 7.1).
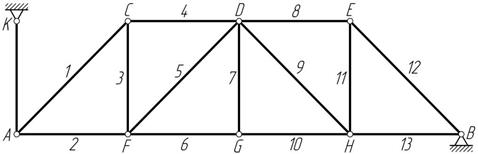
1, 4, 8, 12 – стержни верхнего пояса.
2, 6, 10, 13 – стержни нижнего пояса.
3, 7, 11 – стойки.
5, 9 – раскосы.
Стержень AK называется опорным. Расстояние AB – пролет фермы.
Расчет фермы сводится к определению усилий в опорах фермы и в ее стержнях под действием внешних нагрузок. Для упрощения расчета фермы принимаем некоторые допущения:
1) стержни, из которых состоит ферма, прямолинейны и невесомы;
2) узлы выполнены в виде шарниров без трения;
3) внешние нагрузки приложены к узлам.
Вследствие этих допущений, усилия в стержнях направлены вдоль осей стержней, т.е. стержни работают только на растяжение или на сжатие.
Перед началом расчета фермы необходимо вычислить статическую определимость фермы:
k = 2m - 3,
где k – число стержней (опорные стержни не учитываются);
m – число узлов.
k 2m - 3, то ферма статически неопределима.
Существует несколько методов (способов) расчета ферм:
1) метод вырезания узлов (аналитический и графический);
2) метод Риттера (метод сечений);
3) метод Максвелла-Кремоны.
Леммы о нулевых стержнях
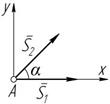
Существуют способы позволяющие определить нагрузку в некоторых стержнях фермы без расчета.
1. Если в незагруженном узле сходятся два стержня
a ¹ 180° , то усилия в них равны нулю

2. Если в незагруженном узле сходятся три стержня, причем два из них лежат на одной прямой, а третий под углом к ним (a ¹ 180° ), то усилие в третьем равно нулю, а усилия в первых двух будут
равны между собой (рисунок 7.3):
S1 = S2 ;
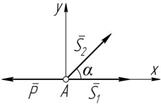
3. Если в загруженном узле сходятся два стержня под углом a ¹ 180° , причем линия действия внешней силы совпадает с осью одного из стержней, то усилие во втором будет равно нулю, а в первом равно
внешней силе (рисунок 7.4):
S1 = P ;
Пример. Определить нулевые стержни с помощью лемм (рисунок 7.5).
BK – опорный стержень.
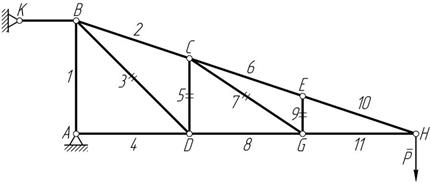
Рисунок 7.5
Рассматривая поочередно узлы E , G , C , и D получим, что стержни
Читайте также:

