Операция логического отрицания и ее свойства кратко
Обновлено: 04.07.2024
Процесс умножения в логических операциях (понятие о конъюнкции и пересечениях)
Умножение в логических процессах — сложная и трудоемкая операция, не всегда являющаяся истиной. Обязательное и единственное условие для такого результата - истина пары простых выражений и ложность всех остальных ситуаций умножения.
Конъюнкция как логическая операция и истина для процесса конъюнкции отражена в таблице номер 1:
Логическое умножение и основные качества конъюнкции:
- Конъюнкция не будет являться истиной в данной выборке, при условии в котором, хотя бы один её подпункт не является истиной среди нескольких данных переменных.
- Весь процесс умножения не является ложным, при условии истинности этого процесса умножения на определенном отрезке переменных.
- Вне зависимости от последовательности представления подпунктов весь процесс умножения будет неизменным.
Процесс сложения в логических операциях (понятие о дизъюнкции и объединениях)
Объемный логический процесс, обладающий практически постоянным свойством истинности (кроме ситуаций, когда все варианты являются ложью) — это дизъюнкция.
Процесс истинности в процессе сложения представлен в таблице:
Дизъюнкция и свойства для нее:
- Весь процесс сложения в логических операциях становится истинным для имеющийся выборки, при условии, что хотя бы единственная её составляющая имеет дизъюнкцию - истину.
- Дизъюнкция будет носить ложный характер, в ситуации при которой все выборки на некотором отрезке данных — ложь.
- Вне зависимости от последовательности представления подпунктов — значение результатов процесса сложения будет оставаться неизменным.
Процесс отрицания в логических операциях (понятие о логических отрицаниях)
Обозначения в тексте:
Логическое отрицание и/или инверсия в таблице истинности:
Свойства процесса отрицания:
Процесс следования в логических операциях (понятие об импликации)
Импликация в логике это обширная последовательность, являющаяся истиной практически всегда; единственное исключение в данной ситуации – это вытекание непосредственной лжи из первоначальной истины. Таким образом логическое следование образует взаимосвязь между парой простейших логических выводов, со следующим видом представления: первый компонент – условие, второй компонент – вывод из этого условия.
Импликация. Логическое выражение представлено в таблице истинности:
Процесс следования обладает следующими свойствами:
Процесс равнозначности в логических операциях (понятие об логических равнозначностях и эквивалентности)
Эквивалентность в логике – сложная структура логического характера, являющееся истиной в одинаковых данных переменных .
Обозначается следующим образом: .
Процесс равнозначности можно представить в таблице истинности:
Равнозначность/эквивалентность имеет ряд особенностей:
- Процесс равнозначности является истинным на наборе переменных . одинакового отрезка
- КНФ .
- ДНФ .
Логические операции и процесс сложения по модулям (понятие о строгой дизъюнкции и об совокупностях пары множеств в отсутствии пересечений, логическое сложение)
Строгий процесс сложения по модулям не будет являться ложью лишь при наличии неравнозначных аргументов.
Если имеется выборка, которая содержит более двух переменных, итог выполненного исчисления будет истинным лишь при наличии числа аугментов строго равным единице, а количество таких выборок обязательно – нечетное число.
Обозначение происходит следующим образом:
- . – если используется любой язык программирования
- . – если используется любой язык программирования
Процесс истинности при операциях дизъюнкции представлен в следующей таблице:
Свойства, характерные для процесса сложения по модулям:
- . – процесс идемпотентности
- . – процесс отрицания
- . – процесс получения нуля
- . – процесс ассоциотивности
- . – процесс коммутативности
- . – процесс поглощения
- . – процесс сравнения по модулю
Стрелка Пирса
Истинность для функции стрелки Пирса представлена следующей таблице:
Основные свойства стрелки Пирса:
- 1. Данное понятие, наряду с понятиями о конъюнкции, дизъюнкции, отрицании, является краеугольным для понимания бинарного функционала пары переменных.
- 2. Стрелка Пирса является начальным проводником и основой для создания любого другого логического оператора. К примеру: . – отрицание, . – дизъюнкция, . – конъюнкция, . – импликация.
Стрелка Пирса – частый представитель электронных носителей, где имеет собственное обозначение .
Штрих Шеффера
Функционал истины для данного понятия представлен в таблице:
Основные свойства штриха Шеффера:
- 1. Данное понятие – краеугольное основание для создания всего бинарного функционала для пары переменных.
- 2. Штрих Шеффера используется как старт для создания других операционных действий. К примеру: . – процесс отрицания, . – процесс конъюнкции, . – процесс дизъюнкции, . – создание константы.
В электронных носителях, применение штриха Шеффера характеризует возможность создание единого привычного элемента. Однако, стоит учитывать высокую материальную затрату при создании подобного варианта.
Последовательность реализации логических действий в операциях сложного логического представления
- 1 этап: Процесс отрицания (процесс инверсии)
- 2 этап: Процесс логического умножения (процесс конъюнкции)
- 3 этап: Процесс логического сложения (процесс строгой дизъюнкции)
- 4 этап: процесс следствия (процесс импликации)
- 5 этап: Процесс тождества (процесс эквивалентности)
Использование такого свойства, как применение скобок может позволить скорректировать представленную последовательность.
Логические операции в информатике: основные функции, признаки. Свойства логических операций
Если представить определенную выборку из . переменных логики можно обнаружить количество разнообразных значений, равных .
Истинность, если представить её в таблице для логического оператора, будет выглядеть как совокупность . столбцов и . строк.
Конъюнкция или логическое умножение (в теории множеств – это пересечение)
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.
Обозначение: &, $\wedge$, $\cdot$.
Таблица истинности для конъюнкции

- Если хотя бы одно из подвыражений конъюнкции ложно на некотором наборе значений переменных, то и вся конъюнкция будет ложной для этого набора значений.
- Если все выражения конъюнкции истинны на некотором наборе значений переменных, то и вся конъюнкция тоже будет истинна.
- Значение всей конъюнкции сложного выражения не зависит от порядка записи подвыражений, к которым она применяется (как в математике умножение).
Дизъюнкция или логическое сложение (в теории множеств это объединение)
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.
Таблица истинности для дизъюнкции

- Если хотя бы одно из подвыражений дизъюнкции истинно на некотором наборе значений переменных, то и вся дизъюнкция принимает истинное значение для данного набора подвыражений.
- Если все выражения из некоторого списка дизъюнкции ложны на некотором наборе значений переменных, то и вся дизъюнкция этих выражений тоже ложна.
- Значение всей дизъюнкции не зависит от порядка записи подвыражений (как в математике – сложение).
Готовые работы на аналогичную тему
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)
Отрицание - означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО и в итоге получаем, что если исходное выражение истинно, то отрицание исходного – будет ложно и наоборот, если исходное выражение ложно, то его отрицание будет истинно.
Обозначения: не $A$, $\bar$, $¬A$.
Таблица истинности для инверсии

Импликация или логическое следование
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).
Обозначения: $\to$, $\Rightarrow$.
Таблица истинности для импликации

- $A \to B = ¬A \vee B$.
- Импликация $A \to B$ ложна, если $A=1$ и $B=0$.
- Если $A=0$, то импликация $A \to B$ истинна при любом значении $B$, (из лжи может следовать истинна).
Эквивалентность или логическая равнозначность
Эквивалентность - это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.
Обозначения: $\leftrightarrow$, $\Leftrightarrow$, $\equiv$.
Таблица истинности для эквивалентности

- Эквивалентность истинна на равных наборах значений переменных $A$ и $B$.
- КНФ $A \equiv B = (\bar \vee B) \cdot (A \cdot \bar)$
- ДНФ $A \equiv B = \bar \cdot \bar \vee A \cdot B$
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов равных $1$, составляющих текущий набор — нечетное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Обозначения: $A \oplus B$ (в языках программирования), $A≠B$, $A \wedge B$ (в языках программирования).
Таблица истинности для операции сложения по модулю два

Свойства строгой дизъюнкции:
- $a \oplus 0 = a$(идемпотентность)
- $a \oplus 1 = \bar$(отрицание)
- $a \oplus a = 0$(получение 0)
- $a \oplus b = b \oplus a$(коммутативность)
- $(a \oplus b) \oplus c = a \oplus (b \oplus c)$(ассоциативность)
- $(a \oplus b) \oplus b = a$(поглощение)
- $\bar \oplus b = a \oplus \bar = (a \equiv b)$(сравнения по модулю)
Стрелка Пирса
Бинарная логическая операция, булева функция над двумя переменными. Названа в честь Чарльза Пирса и введена в алгебру логики в $1880—1881$ гг.
Обозначения: $\downarrow$ , ИЛИ-НЕ
Таблица истинности для стрелки Пирса

Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X \downarrow X = ¬X$— отрицание
$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция
$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция
$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Обозначения: $|$, эквивалентно операции И-НЕ.
Таблицей истинности для функции штрих Шеффера

Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X \mid X = ¬X$ — отрицание
$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция
$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
- Инверсия(отрицание);
- Конъюнкция (логическое умножение);
- Дизъюнкция и строгая дизъюнкция (логическое сложение);
- Импликация (следствие);
- Эквивалентность (тождество).
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.
Общие свойства
Для набора из $n$ логических переменных существует ровно $2^n$ различных значений. Таблица истинности для логического выражения от $n$ переменных содержит $n+1$ столбец и $2^n$ строк.
Эта лицензия позволяет другим редактировать, поправлять и брать за основу ваше произведение в некоммерческих целях до тех пор пока они указывают вас в качестве автора и лицензируют их новые творения на идентичных условиях.
Основы логики. Логические операции и таблицы истинности
На данной странице будут рассмотрены 6 логических операций: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность и исключающие или, которых вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции.
Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬ A.
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
6) Операция XOR (исключающие или)
Обозначение: F = A ⊕ B .
| A | B | F |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Таблицы истинности можно составить и для произвольной логической функции F(a, b, c…).
В общем случае таблицы истинности имеют размер 2 N строк комбинаций для N независимых логических переменных.
Поскольку таблица истинности выражения состоит из строк со всеми возможными комбинациями значений переменных, она полностью определяет значение выражения.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
Замена операций импликации и эквивалентности
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Так, заменить операцию импликации можно в соответствии со следующим правилом:
A → B = ¬ A \/ B
Для замены операции эквивалентности существует два правила:
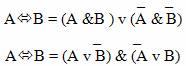
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.
Логические операции в создании компьютерных программ — действия, которые производятся над входными данными. Такие функции производятся над сигналами булевского типа, то есть над примитивными выражениями, имеющими только два возможных значения: истина или ложь.
Виды операций
В программировании выделяют следующие виды функций:
- Логическое умножение или конъюнкция.
- Логическое сложение или дизъюнкция.
- Логическое отрицание или инверсия.
- Логическое следование или импликация.
- Логическая равнозначность или эквивалентность.
- Стрелка Пирса.
- Штрих Шеффера .
Логическое умножение (конъюнкция)
Конъюнкция — это действие, в результате которого каждым двум входным данным соответствует одно новое высказывание. Истинное значение на выходе получается, когда оба входных значения истинны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Таблица истинности для логического умножения выглядит так:
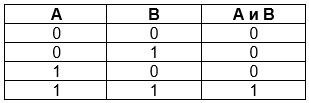
A, B — исходные данные;
A и B — значение, приобретаемое в результате реализации конъюнкции.
Из таблицы следуют свойства логического умножения:
- при ложном значении одной входной информации из двух конъюнкция будет ложной;
- при истинном значении переменных конъюнкция будет истинной;
- результат логического умножения не зависит от порядка записи ее переменных.
Логическое сложение (дизъюнкция)
Дизъюнкция — это булева функция, в итоге которой выходные данные будут ложными только при ложности всех исходных выражений.
Таблица истинности логического сложения:
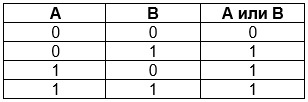
A, B — входная информация;
A или B — значение, приобретаемое в результате выполнения дизъюнкции.
Для дизъюнкции справедливы следующие утверждения:
- при истинности хотя бы одного подвыражения дизъюнкция будет истинной;
- при ложности всех высказываний дизъюнкция примет ложное значение;
- итог дизъюнкции не зависит от перемены мест слагаемых.
Логическое отрицание (инверсия)
Инверсия — выражение, ставящее в соответствие одному значению противоположное.
Таблица истинности инверсии:
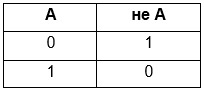
A — исходные данные;
не A — значение, приобретаемое в результате логического отрицания.
Логическое следование (импликация)
Импликация — это булева операция, ложная лишь тогда, когда первая исходная переменная является истиной, а вторая — ложью.
Следование записывается с помощью знака \(\rightarrow.\)
Таблица истинности для импликации:
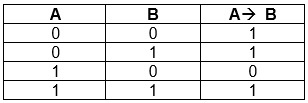
A — входная информация, означающая условие;
B — входная информация, означающая следствие;
A → B — значение, приобретаемое в результате импликации.
Логическая равнозначность (эквивалентность)
Эквивалентность — выражение, являющееся истинным лишь в случае равенства двух входных элементов.
При записи равнозначности используют стрелки \(\Leftrightarrow\) , \(\leftrightarrow\) , \(\Xi\) .
Таблица истинности для равнозначности:
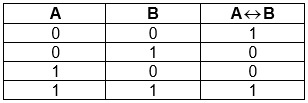
Стрелка Пирса
Стрелка Пирса — двухместное логическое действие со следующей последовательностью: сначала над исходными показаниями производится дизъюнкция, затем происходит отрицание полученного результата.
Данная манипуляция является отрицание логического сложения. Свое название рассматриваемая функция получила от своего автора — американского ученого Чарльза Пирса.
Запись стрелки Пирса осуществляется через знак \(\downarrow\) .
Таблица истинности для этой операции следующая:
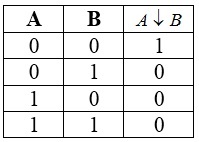
Особенность стрелки Пирса заключается в ее возможности строить другие булевы функции.
Пример
Штрих Шеффера
Штрих Шеффера — это действие, приводящее к ложному итогу лишь при истинности обоих исходных данных. По порядку выполнения операций эта функция эквивалентна отрицанию конъюнкции.
Символ Шеффера назван по фамилии своего создателя — американского логика Генри Шеффера — и обозначается посредством знака \(\vert.\)
Таблица истинности для данной функции:
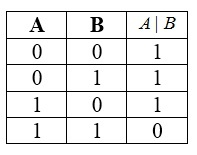
С помощью штриха Шеффера можно воспроизвести другие логические манипуляции.
Пример
Порядок выполнения операций
В составном логическом выражении действия выполняются в такой последовательности:
- инверсия;
- конъюнкция;
- дизъюнкция;
- импликация;
- эквивалентность.
Для построения нужного порядка, как и в математических выражениях, используют скобки.
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Переместительный закон - предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.
Сочетательный закон - применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.
Распределительный закон - имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.
Закон двойственности и инверсии (закон Моргана) - основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
Основные законы алгебры логики представлены в таблице:
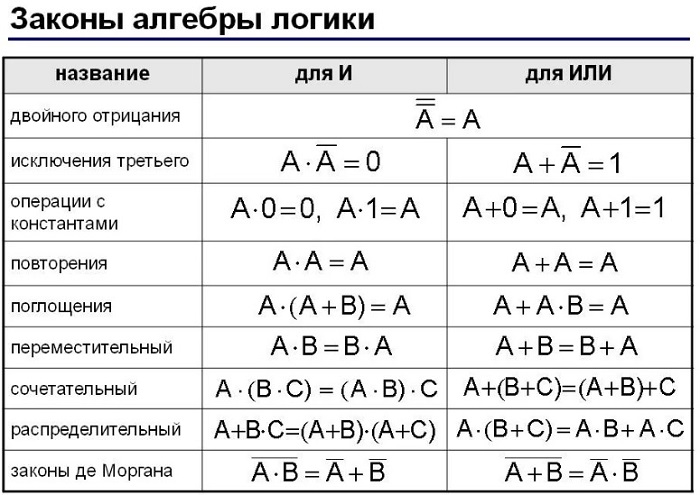
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Нью-Йорк — столица США (ложное);
в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Идёт дождь, а у меня нет зонта.
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
Логическое отрицание (инверсия) —НЕ
Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Таблица истинности операции ИЛИ:
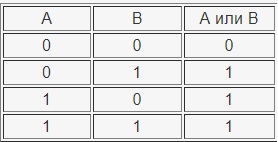
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
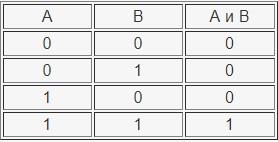
Логическое следование (импликация) — ЕСЛИ ТО
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
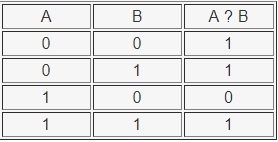
Операция эквивалентности (равнозначности) - А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
Читайте также:

