Свойства параллельных прямых в пространстве кратко

Обновлено: 05.07.2024

Прямые \(a\) и \(b\) являются параллельными в трехмерном пространстве только в том случае, если они находятся в одной плоскости и не пересекаются.

Если рассмотреть примеры, то параллельные прямые мы можем наблюдать как противоположные края у прямоугольного или квадратного стола, железнодорожные рельсы и шпалы, провода линий электропередач, линии в тетради в полоску и прочее. Таких примеров из реального мира можно привести очень много.

Другими вариантами прямых, расположенных в 3D-пространстве, есть их скрещивание и пересечение. Пересекающимися есть прямые, имеющие общую точку, она же и есть точкой пересечения. Скрещивающимися есть прямые, расположенные в разных плоскостях и не параллельные между собой.

Есть ряд теорем, описывающих поведение параллельных прямых в пространстве. Рассмотрим их подробнее.

Теоремы о параллельности двух прямых

если две прямые в пространстве перпендикулярные к одной плоскости, то они параллельные между собой;
через точку в пространстве, что не расположена на заданной прямой, возможно провести лишь одну прямую, параллельную заданной.

Доказательство теоремы : Через прямую a и точку \(M\) , не находящуюся на данной прямой, проведем плоскость ∝. Эта плоскость определяется заданной прямой a и точкой \(M\) , то есть она однозначно определена.

Для доказательства этой теоремы применим евклидовую аксиому из планиметрии про параллельные прямые.
Таким образом, через точку \(M\) возможно проложить лишь одну прямую, параллельную прямой \(a\) , и ее существование доказано. Назовем эту прямую \(b\) .
Два отрезка будут параллельными при их расположении на параллельных прямых.

Свойства параллельных прямых в пространстве

Некоторые свойства пересекаются с вышеизложенными теоремами, но все же рассмотрим их все:

имея две параллельных прямых, одна из которых параллельная третьей прямой, можно утверждать, что вторая тоже будет параллельна третьей;
если из двух параллельных прямых одна пересекает некую плоскость, то и вторая так же будет ее пересекать. Это свойство является леммой про две параллельные прямые в пространстве, ее применяют при обоснованиях различных геометрических теорем;
при помощи двух параллельных прямых можно изобразить однозначно заданную плоскость;
через любую точку, находящуюся в 3D-пространстве и не расположенную на заданной прямой, возможно провести лишь одну прямую, что параллельна заданной.

Рассмотрим подробнее лемму про параллельные прямые и докажем ее. К примеру, некая прямая \(b\) пересекает плоскость \(∝\) в точке \(M\) , что расположена на заданной плоскости. Параллельные прямые a и образуют некую плоскость \(β\) . Таким образом, если точка \(M\) общая для плоскостей \(∝\) и \(β\) , то эти плоскости пересекаются, линию пересечения обозначим c, на ней расположена точка \(M\) .
Все прямые \(a\) , \(b\) и \(c\) расположены в плоскости \(β\) .

Не нашли что искали?

Просто напиши и мы поможем

В соответствии с аксиомой планиметрии, при пересечении одной из параллельных прямых третьей прямой, вторая так же будет ее пересекать.

В нашем варианте прямая a пересекает прямую c в точке \(K\) .

Точка \(K\) расположена одновременно на прямой a и на плоскости \(∝\) , значит она есть общей для них. Таким образом, прямая a пересекает плоскость \(∝\) .

Пример задачи о параллельных прямых

Заданы прямые \(a\) и \(b\) , описывающиеся уравнениями. Определить, параллельны ли заданные прямые.
\(a: <(x-1)\over 1>=<(y-1)\over 3>= <(z+1)\over (-2)>\) ;

При совпадении прямых или если они параллельны их направляющие векторы \(s_1\) и \( s_2\) будут коллинеарными, таким образом, их координаты будут иметь следующее соотношение:

Для того, чтобы найти направляющие вектора, воспользуемся каноническими уравнениями, таким образом для прямой a вектор \(s_1\) будет равен .

Для прямой b найдем направляющий вектор при помощи произведения нормальных векторов плоскостей, на которых он расположен:

Таким образом, соблюдается вышеуказанное условие, значит эти прямые либо параллельны, либо совпадают. Необходимо определить каковыми именно они являются: параллельны или совпадают. Возьмем некую точку \(K\) с координатами (1;2;-1), находящуюся на прямой a, и подставим ее координаты в уравнение прямой \(b\) :
1-2+1+1=0;1=0,

Равенство не выполняется, таким образом, точка \(K\) не расположена на прямой \(b\) , а это означает, что прямые \(a\) и \(b\) не совпадают, соответственно они параллельны.

1. так как прямые \(a\) и \(b\) параллельны, из определения следует, что через них можно провести плоскость α .

2. Чтобы доказать, что такая плоскость только одна, на прямой \(a\) обозначаем точки \(B\) и \(C\), а на прямой \(b\) — точку \(A\).

3. Так как через три точки, которые не лежат на одной прямой, можно провести только одну плоскость (\(2\) аксиома), то α является единственной плоскостью, которой принадлежат прямые \(a\) и \(b\).

Теорема 2. Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и притом только одну.

2. Такая плоскость только одна (т. к. через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну).

3. А в плоскости α через точку \(M\) можно провести только одну прямую \(b\), которая параллельна прямой \(a\).

Теорема 3. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

рассмотрим две параллельные прямые \(a\) и \(b\) и допустим, что прямая \(b\) пересекает плоскость α в точке \(M\) (1 рис.).

Из \(1\)-й теоремы известно, что через параллельные прямые \(a\) и \(b\) можно провести только одну плоскость β .

Так как точка \(M\) находится на прямой \(b\), то \(M\) также принадлежит плоскости β (2 рис.). Если у плоскостей α и β есть общая точка \(M\), то у этих плоскостей есть общая прямая \(c\), которая является прямой пересечения этих плоскостей (\(4\) аксиома).

Если в этой плоскости одна из параллельных прямых \(b\) пересекает прямую \(c\), то вторая прямая \(a\) тоже пересекает \(c\).

Так как точка \(K\) находится на прямой \(c\), то \(K\) находится в плоскости α и является единственной общей точкой прямой \(a\) и плоскости α .

Через точку \(M\) и прямую \(a\), которая не содержит эту точку, можно провести только одну плоскость α (через прямую и не лежащую на ней точку можно провести только одну плоскость).

Значит, прямая \(c\), которая параллельна прямой \(b\), тоже пересекает плоскость α . Так как a ∥ c , то получается, что \(a\) тоже пересекает эту плоскость. Но прямая \(a\) не может одновременно пересекать плоскость α и находиться в плоскости α . Получаем противоречие, следовательно, предположение, что прямая \(b\) пересекает плоскость α , является неверным.

Это означает, что через точку \(L\) проведены две прямые \(a\) и \(b\), которые параллельны прямой \(c\). Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые \(a\) и \(b\) не имеют общих точек.

Так как прямые \(a\) и \(b\) находятся в одной плоскости α , и у них нет общих точек, то они параллельны.

Всё множество прямых в пространстве, которые параллельны данной прямой, называется пучком параллельных прямых .

2) Параллельности прямых в пространстве присуща транзитивность: если a ∥ b и b ∥ c , то a ∥ c .

одна сторона параллелограмма пересекает плоскость. Докажите, что прямая, которая содержит противоположную сторону параллелограмма, тоже пересекает эту плоскость.

Так как противоположные стороны параллелограмма параллельны, то, согласно третьей теореме, прямая, которая содержит сторону \(CD\), тоже пересекает плоскость α .

Доказательство:
доказательство проведём от противного. Пусть \(a\) не параллельна плоскости α , тогда прямая \(a\) пересекает плоскость в некоторой точке \(A\). Причём \(A\) не находится на \(b\), так как a ∥ b . Согласно признаку скрещивающихся прямых, прямые \(a\) и \(b\) — скрещивающиеся.

Мы пришли к противоречию. Так как согласно данной информации a ∥ b , они не могут быть скрещивающимися. Значит, прямая \(a\) должна быть параллельна плоскости α .

Теорема 6.
Если плоскость β проходит через данную прямую \(a\), параллельную плоскости α , и пересекает эту плоскость по прямой \(b\), то b ∥ a .

Есть ряд теорем, описывающих поведение параллельных прямых в пространстве. Рассмотрим их подробнее.

Теоремы о параллельности двух прямых

если две прямые в пространстве перпендикулярные к одной плоскости, то они параллельные между собой;
через точку в пространстве, что не расположена на заданной прямой, возможно провести лишь одну прямую, параллельную заданной.

Свойства параллельных прямых в пространстве

Некоторые свойства пересекаются с вышеизложенными теоремами, но все же рассмотрим их все:

имея две параллельных прямых, одна из которых параллельная третьей прямой, можно утверждать, что вторая тоже будет параллельна третьей;
если из двух параллельных прямых одна пересекает некую плоскость, то и вторая так же будет ее пересекать. Это свойство является леммой про две параллельные прямые в пространстве, ее применяют при обоснованиях различных геометрических теорем;
при помощи двух параллельных прямых можно изобразить однозначно заданную плоскость;
через любую точку, находящуюся в 3D-пространстве и не расположенную на заданной прямой, возможно провести лишь одну прямую, что параллельна заданной.

Не нашли что искали?

Просто напиши и мы поможем

В нашем варианте прямая a пересекает прямую c в точке \(K\) .

Пример задачи о параллельных прямых

Заданы прямые \(a\) и \(b\) , описывающиеся уравнениями. Определить, параллельны ли заданные прямые.
\(a: = = \) ;

Параллельные прямые в пространстве. Параллельность трех прямых

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы дадим основные определения и теоремы на тему параллельных прямых в пространстве.
В начале урока рассмотрим определение параллельных прямых в пространстве и докажем теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной. Далее докажем лемму о двух параллельных прямых, пересекающих плоскость. И с ее помощью докажем теорему о двух прямых, параллельных третьей прямой.

Свойства параллельных прямых в пространстве (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8

Тема: Свойства параллельных прямых в пространстве

Возможны четыре различных случая расположения двух прямых в пространстве:

прямые скрещивающиеся, т. е. не лежат в одной плоскости; прямые пересекаются, т. е. лежат в одной плоскости и имеют одну общую точку; прямые параллельные, т. е. лежат в одной плоскости и не пересекаются; прямые совпадают.

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

a||b (прямая а параллельна прямой b)

Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Отрезок отрезок CD ||AB

Свойства параллельных прямых

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

2. Если две прямые параллельны третьей прямой, то они параллельны.

Задание№1. Ответить на вопросы:

Две прямые пересекаются. Что это значит? Две прямые называются скрещивающимися, если. Две прямые в пространстве называются параллельными, если. Прямая а, параллельная прямой b, пересекает плоскость б. Прямая с параллельна прямой b, тогда: Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b? Каким может быть взаимное расположение двух прямых, если обе они параллельны одной плоскости?

Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:

1) Прямые СD и MN скрещивающиеся.

2) Прямые АВ и MN лежат в одной плоскости.

3) Прямые СD и MN пересекаются.

4) Прямые АВ и СD скрещивающиеся.

Задание №3. С учебника

Домашняя работа: С учебника

Что называется пересекающимися прямыми? Что называется скрещивающимися прямыми? Что называется параллельными прямыми?

Задание СРС: Виды расположения прямых.

Тема: Признак скрещивающихся прямых.

Возможны четыре различных случая расположения двух прямых в пространстве:

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

скрещивающиеся прямые a⊂б, b∩б=K, K∉a⇒a и b−скрещивающиеся прямые

Задание №1. Определите взаимное расположение прямых иa и b.

Задание №2. Точки А, В, С и D – середины ребер прямоугольного параллелепипеда. Найдите параллельные прямые.

Задание №3. Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых иa и b.

Задание №3. С учебника

Домашняя работа: С учебника

Задание СРС: Взаимное расположение в плоскости.

Тема: Взаимное расположение прямой и плоскости.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек (а || )

Выводы.
Случаи взаимного расположения прямой и плоскости:

а) прямая лежит в плоскости;

б) прямая и плоскость имеют только одну общую точку;

в) прямая и плоскость не имеют ни одной общей точки.

Дан треугольник ABC. На сторонах AB и AC соответственно отложены точки D и E так, что DE=7 см и ADBD=94. Через точки B и C проведена плоскость б, которая параллельна отрезку DE.

Основание AB трапеции ABCD лежит в плоскости б. Основание CD не лежит в этой плоскости.

Дополни данные предложения, которые характеризуют взаимное расположение данных прямых и плоскости б.

1.Tак как прямая DB имеет общую точку с данной плоскостью, то эта прямая б

2.Прямая CD параллельна прямой AB в данной плоскости, значит онаб

Задание№3. Определи взаимное расположение данной прямой и плоскости.

1. Прямая AA1 и плоскость (BCD):

2. Прямая BC и плоскость (ABC):

3. Прямая CC1 и плоскость (ABD):

4. Прямая CB1 и плоскость (BB1C1):

5. Прямая AB1 и плоскость (BCD):

Задание №4. С учебника

Домашняя работа: С учебника

Когда называются прямая и плоскость прямыми? Назовите случаи взаимного расположения прямой и плоскости. Что называется параллельными прямыми?

Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.

Признак параллельности прямых

Две прямые, параллельные третьей, параллельны между собой.

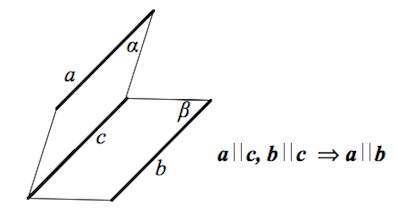
Параллельные прямая и плоскость

Прямая и плоскость называются параллельными , если они не имеют общих точек.

Признак параллельности прямой и плоскости

Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.

Свойство прямой, параллельной данной плоскости

Если плоскость β проходит через прямую a , параллельную плоскости α , и пересекает эту плоскость по прямой b , то b || a .

Параллельные плоскости

Параллельные плоскости – плоскости, которые не пересекаются.

Признаки параллельности плоскостей

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.

Свойства параллельных плоскостей

Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

Читайте также: