Несобственные интегралы это кратко

Обновлено: 05.07.2024

Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен, а подынтегральная функция ограничена на нем — в противном случае множество сумм Дарбу не будет ограниченным. При решении задач встречаются случаи, когда одно или оба из этих условий не выполняются, т. е. когда промежуток интегрирования бесконечен или подынтегральная функция не ограничена. Такие интегралы называются несобственными. Различают несобственные интегралы 1-го и 2-го рода в зависимости от того, имеем ли мы дело с бесконечностью промежутка интегрирования или с неограниченностью подынтегральной функции.

Хотя несобственные интегралы и нельзя рассматривать как разделяющие числа для сумм Дарбу, иногда им можно придать определенный смысл с помощью дополнительного предельного перехода. Начнем со случая, когда промежутком интегрирования является луч . Предположим, что функция интегрируема на каждой конечной части луча, т. е. что для любого . За значение интеграла естественно принять предел функции , когда с стремится к (рис. 18).

Может, однако, случиться, что этот предел не существует. Поэтому будем различать два случая:

а) Если предел существует и конечен, то несобственный интеграл называют сходящимся, а значение этого предела — значением несобственного интеграла. В этом случае

б) Если предел в правой части равенства (1) не существует, говорят, что несобственный интеграл расходится.

При аналогичных предположениях относительно функции можно рассмотреть случай, когда верхний предел фиксирован, а нижний предел стремится к

Если предел, стоящий в правой части равенства (2), конечен, то несобственный интеграл называют сходящимся, в противном случае его называют расходящимся.

Наконец, можно определить и несобственный интеграл вида . Будем считать, что функция интегрируема на всей числовой прямой . Выберем на прямой произвольную точку и . Если существуют несобственные интегралы

то говорят, что существует и несобственный интеграл . В этом случае полагают

где несобственные интегралы, содержащиеся в правой части равенства (3), определены соответственно равенствами (1) и (2). Легко проверить, что значение интеграла не зависит от выбора точки

Пример 1. Вычислить несобственный интеграл с бесконечным верхним пределом.

Решение. Подынтегральная функция всюду непрерывна и, следовательно, интегрируема в любом конечном промежутке. Имеем:

Значит, окончательно имеем .

Пример 2. Вычислить несобственный интеграл от синуса .

Так как не существует, то несобственный интеграл расходится.

Запись вычислений несобственных интегралов можно упростить, предварительно найдя первообразную для подынтегральной функции . Именно, если —первообразная функция для , то

Предположим, что существует предел . Введем обозначение: . Тогда

Пример 3. Вычислить несобственный интеграл .

Пример 4. Исследовать на сходимость несобственный интеграл .

Сходимость или расходимость интеграла зависит от того, существует или нет предел . Если ; если . Таким образом, сходится, если

При исследовании на сходимость несобственных интегралов оказываются полезными следующие утверждения:

а) Если сходится интеграл , то при . При этом

б) Если сходятся интегралы и , то и интеграл сходится, причем

Признаки сходимости несобственных интегралов 1-го рода

В дальнейшем мы будем обычно иметь дело с несобственными интегралами от неотрицательных функций. Если функция неотрицательна на луче , то функция возрастает на этом луче. Поэтому она имеет предел при в том и только в том случае, когда ограничена. Отсюда получаем следующее утверждение:

а) Для сходимости несобственного интеграла от неотрицательной функции , необходимо и достаточно, чтобы функция была ограничена, т. е. чтобы нашлось такое число , что для всех .

Непосредственно найти такое число бывает довольно сложно, поэтому во многих случаях оказывается полезным следующее утверждение:

б) Если на луче выполняется неравенство и интеграл сходится, то сходится и интеграл .

В самом деле, из следует, что для любого

Но функция возрастает, и потому ее предел при не меньше любого из ее значений: . Поэтому для всех имеем: , где . А тогда на основании предыдущего утверждения интеграл сходится.

Из доказанного вытекает, что если при и интеграл расходится, то расходится и интеграл — в противном случае в соответствии с утверждением б) интеграл сходился бы.

Пример 5. Исследуем на сходимость интеграл .

Решение. Мы имеем при сходится (см. пример 4). Поэтому сходится и исходный интеграл.

Пример 6. Исследуем на сходимость интеграл .

Решение. Так как при расходится (см. пример 4 при ), то расходится и заданный интеграл.

Несобственные интегралы 2-го рода

Рассмотрим теперь случай, когда промежуток интегрирования конечен, но подынтегральная функция не ограничена на нем. Строение таких функций может быть очень сложным. Мы ограничимся рассмотрением случая, когда можно указать конечное множество особых точек , таких, что в сколь угодно малых окрестностях этих точек функция не ограничена, но после удаления этих окрестностей получаем промежутки, на которых функция интегрируема.

Сначала изучим случай, когда множество особых точек состоит лишь из точки не ограничена на всем отрезке , но интегрируема на любом из отрезков (рис. 19). За значение интеграла естественно принять предел , если этот предел существует.

Введем следующее определение:

Пусть функция не ограничена на отрезке , но интегрируема на любом из отрезков , где . Несобственный интеграл называют сходящимся, если существует предел . Значение этого предела и называют значением интеграла . Если же этот предел не существует, то интеграл называют расходящимся.

Аналогично, если функция не ограничена на отрезке , но интегрируема на любом отрезке , то полагаем

Наконец, если единственная особая точка лежит внутри отрезка , то положим

Пусть — первообразная для функции . Положим

(если эти пределы существуют). Тогда для сходящихся интегралов, у которых особыми являются лишь точки

Если функция непрерывна в точках

Аналогично обстоит дело и в случае, когда подынтегральная функция не ограничена в любой окрестности некоторой внутренней точки отрезка .

Пример 7. Вычислим несобственный интеграл второго рода .

Решение. Этот интеграл является несобственным, так как функция не ограничена в любой окрестности точки

откуда, учитывая непрерывность функции

Пример 8. Вычислить интеграл .

Решение. Подынтегральная функция внутри данного промежутка интегрирования имеет одну особую точку . Найдем первообразную для подынтегральной функции:

Так как функция непрерывна в точке , то имеем

Пример 9. Вычислить .

Решение. В данном случае подынтегральная функция имеет две особые точки и . Пользуясь определением несобственного интеграла и учитывая непрерывность первообразной, получаем, что

К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределов и графиков элементарных функций. По логике изложения материала эта статья является продолжением урока Определенный интеграл. Как вычислить площадь фигуры.

Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….

Что значит вычислить несобственный интеграл?

Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).

Несобственные интегралы бывают двух видов.

Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда такой несобственный интеграл называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус :)

Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:

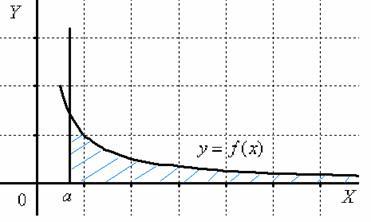
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади. При этом возможны следующие варианты:

2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится.

3) О третьем варианте чуть позже.

В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.

А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.

Таким образом, несобственный интеграл может быть отрицательным.

Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.

Коль скоро несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .

В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений, ибо лучше поздно, чем в армии.

Рассмотрим два классических примера:

Вычислить несобственный интеграл или установить его расходимость.

Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.

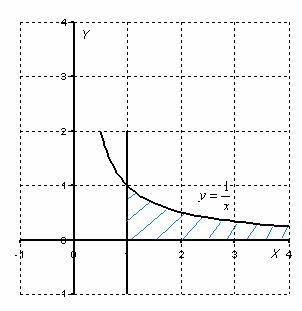
Применение нашей формулы и решение задачи выглядит так:

То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций.

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

Подынтегральная функция непрерывна на

Несобственный интеграл расходится.
“

! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.

Вычислить несобственный интеграл или установить его расходимость.

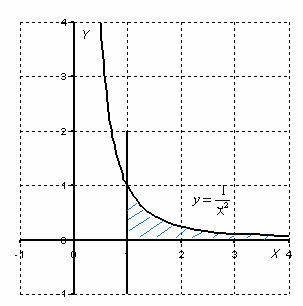
Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :

(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

Подынтегральная функция непрерывна на

Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего), либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности, следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.

Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция непрерывна на .

Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.

Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.

На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.

Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

Подынтегральная функция непрерывна на .

А сейчас два примера для самостоятельного решения.

Вычислить несобственный интеграл или установить его расходимость.

! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей.

Вычислить несобственный интеграл или установить его расходимость.

Полные решения и ответы в конце урока.

Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов. Там же разобран случай, когда оба предела интегрирования бесконечны.

Несобственные интегралы от неограниченных функций

Если подынтегральной функции не существует в точке

Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: . Здесь всё хорошо.

Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

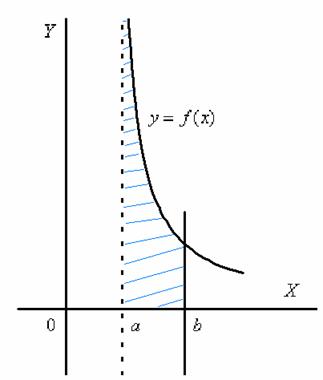
Здесь почти всё так же, как в интеграле первого рода.

Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

* по умолчанию привычно полагаем, что несобственный интеграл существует

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа.

Посмотрим, как это реализуется на практике.

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)

Сначала вычислим неопределенный интеграл:

У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле.

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .

А сейчас два примера для самостоятельного решения.

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:

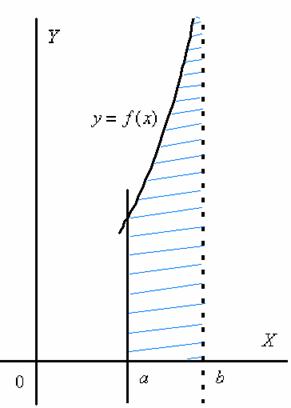
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению слева. По оси мы должны бесконечно близко приблизиться к точке разрыва слева.

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечный разрыв в точке (устно проверяем, что с другим пределом интегрирования всё нормально!).

Для разнообразия я решу этот интеграл сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.

Добавка обозначает, что предел у нас левосторонний, и к точке мы приближаемся по оси слева.

Разбираемся, почему дробь (это лучше делать устно или на черновике).
Подставляем под корень предельное значение :
и тогда

Несобственный интеграл расходится.

Будьте очень внимательны в знаках. Да, конечно, несобственный интеграл расходится, но и – это разные вещи, разные жанры, и если Вы недосмотрите за знаками, то, строго говоря, допустите серьезную ошибку.

И заключительные два примера для самостоятельного рассмотрения:

Вычислить несобственный интеграл или установить его расходимость.

Решения и ответы:

Пример 4: Решение:

Подынтегральная функция непрерывна на .

Пример 5: Решение:

Подынтегральная функция непрерывна на .

Несобственный интеграл расходится.

Пример 7: Решение:

Подынтегральная функция терпит бесконечный разрыв в точке

Несобственный интеграл расходится.

Примечание: с пределом выражения можно разобраться следующим образом: вместо подставляем :

Пример 8: Решение:

Подынтегральная функция терпит бесконечный разрыв в точке

Примечание: Разбираемся в пределе выражения . Если , то (см. график логарифмической функции!), тогда: . Именно эти соображения и помечаются как

Пример 10: Решение:

Подынтегральная функция терпит бесконечный разрыв в точке

Пример 11: Решение:

Подынтегральная функция терпит бесконечный разрыв в точке

Несобственный интеграл расходится

Примечание: Разбираемся в пределе выражения . Если , то , и тогда . Будьте очень внимательны в знаках!

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Такие интегралы получили название несобственные интегралы первого рода.

Это так называемые несобственные интегралы второго рода.

Что значит решить несобственный интеграл? В отличие от определённого интеграла, тут есть три варианта. Решить несобственный интеграл – это значит найти конечное число, либо получить бесконечность, либо выяснить, что несобственного интеграла не существует.

1) Если несобственный интеграл равен конечному числу, то говорят, что он сходится. Число может быть как положительным, так и отрицательным. Или нулём.

3) И в ряде случаев несобственного интеграла может вовсе не существовать. Даже если подынтегральная функция непрерывна на промежутке интегрирования! (вспоминаем, что определённый интеграл при этом условии существует всегда).

Как решить несобственный интеграл? С помощью той же формулы Ньютона-Лейбница. С некоторыми особенностями.

И здесь вы должны понимать и уметь решать несложные пределы функций.

В чём смысл несобственного интеграла? Геометрически – это тоже площадь (если интеграл существует). Но площадь своеобразная. И с этим своеобразием мы познакомимся прямо на следующей странице:

Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:

Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].

Содержание

Несобственные интегралы I рода

Пусть определена и непрерывна на множестве от и . Тогда:

Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:

$\int\limits_<-\infty> ^ <+\infty>f(x)dx = \int\limits_<-\infty>^ f(x)dx + \int\limits_^ <+\infty>f(x)dx$
, где с — произвольное число.

Геометрический смысл несобственного интеграла I рода

Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.

Примеры

$\int\limits_<-\infty> ^ dx = \lim_ \int\limits_^ dx = \lim_ \Bigl. -\frac \Bigr|_a^ = 1 + \lim_ \frac = 1 + 0 = 1$

Несобственные интегралы II рода

Пусть определена на , терпит бесконечный разрыв в точке x=a и . Тогда:

Пусть определена на , терпит бесконечный разрыв при x=b и . Тогда:

Если функция терпит разрыв во внутренней точке отрезка , то несобственный интеграл второго рода определяется формулой:

$\int\limits_^ f(x)dx = \int\limits_^ f(x)dx + \int\limits_^ f(x)dx$

Геометрический смысл несобственных интегралов II рода

Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции

Пример

$\int\limits_<0> ^ = \lim_ \Bigl. \ln |x| \Bigr|_^1 = 0 - \lim_ \ln \delta = + \infty$

Отдельный случай

Пусть функция определена на всей числовой оси и имеет разрыв в точках .

$\int\limits_<-\infty > Тогда можно найти несобственный интеграл ^ <+\infty>f(x)dx = \int\limits_<-\infty >^ f(x)dx + \sum_^ <\int\limits_<x_j>^> f(x)dx>+ \int\limits_^ <+\infty>f(x)dx$

Критерий Коши

1. Пусть определена на множестве от и .

Тогда =\int\limits_^ <+\infty>f(x)dx" width="" height="" />
сходится

2. Пусть определена на и .

Тогда =\int\limits_^ f(x)dx" width="" height="" />
сходится

Абсолютная сходимость

Интеграл f(x)dx \ \ \left(\int\limits_^ f(x)dx\right)" width="" height="" />
называется абсолютно сходящимся, если |f(x)|dx \ \ \left(\int\limits_^ |f(x)|dx\right)" width="" height="" />
сходится.
Если интеграл сходится абсолютно, то он сходится.

Условная сходимость

Интеграл f(x)dx \ \ " width="" height="" />
называется условно сходящимся, если f(x)dx \ \ " width="" height="" />
сходится, а |f(x)|dx \ \ " width="" height="" />
расходится.

См. также

Список используемой литературы

Дмитрий Письменный Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Несобственный интеграл" в других словарях:

НЕСОБСТВЕННЫЙ ИНТЕГРАЛ — обобщение понятия интеграла на случай неограниченных функций и функций, заданных на бесконечном промежутке интегрирования … Большой Энциклопедический словарь

несобственный интеграл — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN improper integral … Справочник технического переводчика

несобственный интеграл — обобщение понятия интеграла на случай неограниченных функций и функций, заданных на бесконечном промежутке интегрирования. * * * НЕСОБСТВЕННЫЙ ИНТЕГРАЛ НЕСОБСТВЕННЫЙ ИНТЕГРАЛ, обобщение понятия интеграла на случай неограниченных функций и функций … Энциклопедический словарь

НЕСОБСТВЕННЫЙ ИНТЕГРАЛ — интеграл от неограниченной функции или от функции по неограниченному множеству. Пусть функция f определена на конечном или бесконечном полуинтервале , и для любого функция f интегрируема но Риману (по Лебегу) на отрезке Тогда предел (в случае… … Математическая энциклопедия

АБСОЛЮТНО СХОДЯЩИЙСЯ НЕСОБСТВЕННЫЙ ИНТЕГРАЛ — несобственный интеграл, для к рого интеграл от абсолютной величины подинтегральной функции сходится. Если несобственный интеграл абсолютно сходится, то он и просто сходится. Пусть дан (для определенности) несобственный интеграл вида: где функция… … Математическая энциклопедия

Интеграл Курцвейля — Интеграл Курцвейля Хенстока обобщение интеграла Римана, позволяет полностью решить задачу о восстановлении дифференцируемой функции по её производной. Ни интеграл Римана (в том числе и несобственный), ни интеграл Лебега не дают… … Википедия

Интеграл Курцвейля-Хенстока — В математике, Интеграл Курцвейля Хенстока является обобщением интеграла Римана, позволяющим полностью решить задачу о восстановлении дифференцируемой функции по её производной. Ни интеграл Римана (в том числе и несобственный), ни интеграл Лебега… … Википедия

КРАТНЫЙ ИНТЕГРАЛ — определенный интеграл от функции нескольких переменных. Имеются различные понятия К. и. (интеграл Римана, интеграл Лебега, интеграл Лебега Стилтьеса и др.). Кратный интеграл Римана вводится на основе Жордана меры Пусть Е измеримое по Жордану… … Математическая энциклопедия

Римана интеграл — Геометрический смысл интеграла Римана Интеграл Римана одно из важнейших понятий математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла. Содержание 1 Неформальное г … Википедия

Сингулярный интеграл — 1) одно из средств представления функций; под С. и. понимают интеграл вида , который при n → ∞ сходится (при тех или иных ограничениях на функцию f) к порождающей его функции f (х); функция Kn (x, t) называется… … Большая советская энциклопедия

Читайте также: