Инвариантные величины это кратко

Обновлено: 30.06.2024

Из векторов напряженностей электрического и магнитного полей можно составить инвариантные величины, остающиеся неизменными при преобразованиях от одной инерциальной системы отсчета к другой.

Вид этих инвариантов легко найти исходя из четырехмерного представления поля с помощью антисимметричного 4-тензора . Очевидно, что из компонент этого тензора можно составить следующие инвариантные величины:

где — совершенно антисимметричный единичный тензор (см. § 6).

Первая из этих величин — истинный скаляр, а вторая — псевдоскаляр (произведение тензора на дуальный ему тензор).

Выражая компоненты через компоненты Е и Н согласно (23,5), легко убедиться в том, что в трехмерной форме эти инварианты имеют вид

Псевдоскалярность второго из них очевидна из того, что он представляет собой произведение полярного вектора Е на аксиальный вектор Н (квадрат же будет истинным скаляром)

Из инвариантности приведенных двух выражений вытекают следующие выводы. Если в какой-нибудь системе отсчета электрическое и магнитное поля взаимно перпендикулярны, т. е. , то они перпендикулярны и во всякой другой инерциальной системе отсчета. Если в какой-нибудь системе отсчета абсолютные величины Е и Н равны друг другу, то они одинаковы и в любой другой системе.

Имеют, очевидно, место также и следующие неравенства. Если в какой-нибудь системе отсчета то и во всякой другой системе будет (или Если в какой-либо системе отсчета векторы Е и Н образуют острый (или тупой) угол, то они будут образовывать острый (или тупой) угол и во всякой другой системе.

Преобразованием Лоренца можно всегда достичь того, чтобы Е и Н получили любые значения, удовлетворяющие только условию, чтобы и ЕН имели заданные определенные значения. В частности, можно найти такую инерциальную систему отсчета, в которой электрическое и магнитное поля в данной точке параллельны друг другу. В этой системе и из двух уравнений

можно найти значения Е и Н в этой системе отсчета и Но — электрическое и магнитное поля в исходной системе отсчета).

Исключением является случай, когда оба инварианта равны нулю. В этом случае Е и Н во всех системах отсчета равны по величине и взаимно перпендикулярны по направлению.

Если лишь ЕН = 0, то можно найти такую систему отсчета, в которой Е = 0 или Н = 0 (смотря по тому или т. е. поле чисто магнитное или чисто электрическое; наоборот, если в какой-нибудь системе отсчета Е = 0 или Н = 0, то во всякой другой системе они будут взаимно перпендикулярны в соответствии со сказанным в конце предыдущего параграфа.

Изложим еще и другой способ подхода к вопросу об инвариантах антисимметричного 4-тензора. Этот способ делает очевидным единственность двух независимых инвариантов (25,3-4) и в то же время выявляет некоторые поучительные математические свойства преобразований Лоренца в применении к 4-тензору.

Рассмотрим комплексный вектор

Используя формулы (24,2-3), легко видеть, что преобразование Лоренца (вдоль оси х) для этого вектора имеет вид

Мы видим, что вращение в плоскости -пространства (каковым и является рассматриваемое прербразование Лоренца) для вектора F эквивалентно вращению на мнимый угол в плоскости yz трехмерного пространства. Совокупность же всех возможных поворотов в 4-пространстве (включающая в себя также и простые повороты осей х) эквивалентна совокупности всех возможных поворотов на комплексные углы в трехмерном пространстве (шести углам поворота в 4-пространстве соответствуют три комплексных угла поворота трехмерной системы).

Единственным инвариантом вектора по отношению к поворотам является его квадрат Поэтому вещественные величины и ЕН являются единственными инвариантами тензора

Задача

Решение. Систем отсчета удовлетворяющих поставленному условию, существует бесконечное множество: если найдена одна из них, то так же свойством будет обладать и любая другая система, движущаяся относительно первой со скоростью, направленной вдоль общего направления полей Е и Н, Поэтому достаточно определить ту из этих систем, скорость которой перпендикулярна к обоим полям. Выбирая направление скорости в качестве оси х и воспользовавшись тем, что в системе К поля получим с помощью формул для скорости V системы К относительно исходной системы следующее уравнение:

(из двух корней квадратного уравнения должен, разумеется, быть выбран тот, для которого ).

Инвариа́нт — термин, используемый в математике и физике, а также в программировании, обозначает нечто неизменяемое. Кроме того, инварианты используются в олимпиадных задачах по математике для школьников. Абстрактная структурная единица языка - фонема, морфема, лексема и т.п. - в отвлечении от её конкретных реализаций (в лингвистике).

Содержание

Инварианты в математике

Пусть A — множество и G — множество отображений из A в A. Отображение f из A во множество B называется инвариантом для G, если для любых и выполняется тождество f(a) = f(g(a)) .

Концепция инварианта является одной из важнейших в математике, поскольку изучение инварианта непосредственно связано с задачами классификации объектов того или иного типа. По существу, целью всякой математической классификации является построение некоторой полной системы инвариантов (по возможности, наиболее простой), то есть такой системы, которая разделяет любые два неэквивалентных объекта из рассматриваемой совокупности. (В.Л.Попов, Инвариант, Математическая энциклопедия, т.2, М.: Советская энциклопедия, 1979, С. 526.)

Инварианты в олимпиадной математике

Понятие инварианта можно проиллюстрировать на следующей задаче:

Ребёнок овладел всего лишь двумя звуками: "У" и "А", причем два слова в лексиконе этого ребёнка означают одно и то же, если одно получается из другого при помощи следующих преобразований: исключения идущих подряд звуков "УА" или "ААУУ" и добавления в любое место сочетания "АУУА". Докажите, что слова "ААУАААУУА" и "ААУУААА" означают одно и то же.

Нетрудно проверить, что второе слово получается из первого в результате последовательного применения трёх преобразований, указанных выше (назовём их смыслосохраняющими преобразованиями) — надо только найти эту цепочку смыслосохраняющих преобразований. Однако, на вопрос, означают ли слова "АУУ" и "УАА" одно и то же, ответить гораздо сложнее. Перебор последовательностей смыслосохраняющих преобразований не позволит получить второе слово из первого, так как данные слова имеют разный смысл. Для доказательства этого нужен принципиально другой подход, именуемый поиском инварианта. [1] [2]

Инварианты в физике

В физических процессах всегда существуют величины, которые не изменяются с течением времени, они и называются инвариантами. Примеры: энергия, компоненты импульса и момента импульса в замкнутых системах.

Также инвариантами называются величины, независимые от условий наблюдения, в особенности - от системы отсчета - например интервал в теории относительности инвариантен в этом смысле. Промежуток времени между двумя событиями, а также расстояние между ними (местами событий) для наблюдателей, движущихся в различных направлениях с разными скоростями, будут разными, однако интервал между этими событиями для всех наблюдателей будет один. К этой же категории относится, например скорость света в вакууме. Такие величины, в зависимости от класса систем отсчета, при переходе между которыми сохраняется инвариантность данной величины, называют лоренц-инвариантными (инвариантами группы Лоренца) или инвариантами группы общекоординатных преобразований (рассматриваемыми в общей теории относительности); для ньютоновской физики может иметь смысл также рассматривать инвариантность относительно преобразований Галилея (инвариантными относительно таких преобразований являются компоненты ускорения и силы).

Понятие инвариантности (инвариантов) в физике лежит в русле принятого в математике понятия "инвариант преобразований (группы преобразований)" (той или иной конкретной группы преобразований - сдвигов времени, преобразований Лоренца итп).

Инварианты в программировании

Инвариантом называется логическое выражение, истинное после каждого прохода тела цикла (после выполнения фиксированного оператора) и перед началом выполнения цикла, зависящее от переменных, изменяющихся в теле цикла. Инварианты используются в теории верификации программ для доказательства правильности выполнения цикла. Порядок доказательства работоспособности цикла с помощью инварианта сводится к следующему:

Доказывается, что выражение инварианта истинно перед началом цикла.
Доказывается, что выражение инварианта сохраняет свою истинность после выполнения тела цикла; таким образом, по индукции, доказывается, что по завершении цикла инвариант будет выполняться.
Доказывается, что при истинности инварианта после завершения цикла переменные примут именно те значения, которые требуется получить (это элементарно определяется из выражения инварианта и известных конечных значениях переменных, на которых основывается условие завершения цикла).
Доказывается (возможно — без применения инварианта), что цикл завершится, то есть условие завершения рано или поздно будет выполнено.
Истинность утверждений, доказанных на предыдущих этапах, однозначно свидетельствует о том, что цикл выполнится за конечное время и даст желаемый результат.

Также инварианты используют при проектировании и оптимизации циклических алгоритмов. Например, чтобы убедиться, что оптимизированный цикл остался корректным, достаточно доказать, что инвариант цикла не нарушен и условие завершения цикла достижимо.

Понятие инварианта также используется в объектно-ориентированном программировании для обозначения непротиворечивого состояния объекта. Подразумевается, что вызов любого метода оставляет объект в состоянии инварианта.

Инвариант в фольклористике

Инвариантом называется неизменяемая часть сюжета фольклорного произведения, которая характерна для всего сюжетного типа. Инварианту противостоит вариант.

Мы показали, что при переходе из одной системы в другую координаты точки изменяются (координаты относительны). Помимо относительных величин (зависящих от системы координат) имеются величины независящие от системы координат (такие величины называются инвариантными). Примером такой величины является расстояние между двумя точками. Действительно, пусть на плоскости (рис.4) расположены две точки: A₁ с координатами (x₁,y₁) и A₂ с координатами (x₂,y₂).

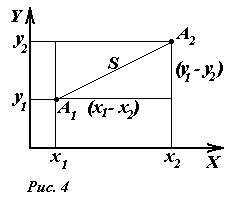
Тогда на основании теоремы Пифагора расстояние между точками может быть вычислено по формуле

При переходе в любую другую систему отсчета (при неизменной единице длины) расстояние, вычисленное по формуле (4), остается неизменным. Например, при сдвиге начала отсчета, описываемом уравнениями (1), все четыре координаты изменятся, но разности одноименных координат, а, следовательно, и расстояние останутся неизменными (инвариантными). Можно указать и другие геометрические инвариантные величины – углы между отрезками, площади и объемы фигур и др. Особенно отметим, что соотношения, записанные в векторной форме, остаются неизменными при преобразованиях координат. Так, например, скалярное произведение [1] двух векторов не зависит от выбора системы координат. В частном случае, скалярное произведение вектора на самого себя равно квадрату длины вектора. Поэтому формула (4) в векторной форме имеет вид

Поиск инвариантных величин, не изменяющихся при преобразованиях координат, представляет большой интерес, а многие физические теории и формулируются в терминах инвариантных величин.

Задание для самостоятельной работы

1. В полярной системе координат положение точки A на плоскости задается с помощью а) расстояния r до начала координат O, б) угла φ, который образует отрезок OA с осью X.

Установите связь между полярными (r,φ) и декартовыми координатами точки.

Выразите расстояние между двумя точками через их полярные координаты.

(от лат. invarians, род. п. invariantis — неизменяющийся), неизменность, независимость от нек-рых физ. условий. Чаще рассматривается И. в матем. смысле — неизменность к.-л. величины по отношению к нек-рым преобразованиям. Напр., если рассматривать движение матер. точки в двух системах координат, повёрнутых одна относительно другой на нек-рый угол, то проекции скорости движения в них будут разными, но квадрат скорости, а следовательно, и кинетич. энергия будут одинаковыми, т. е. кинетич. энергия инвариантна относительно поворота в пр-ве системы отсчёта. Важный случай — И. относительно преобразований Лоренца (релятивистская инвариантность). Примеры таких инвариантов — четырёхмерный интервал, полный электрич. заряд, а также величины Е2-Н2 и E•H в электродинамике, где Е к Н — напряжённости электрич. и магн. полей. В общей теории относительности (теории тяготения) рассматриваются величины, инвариантные относительно произвольных преобразований координат. Особую роль играет И. относительно т. н. калибровочных преобразований (см. КАЛИБРОВОЧНАЯ СИММЕТРИЯ), распространение к-рой на широкий класс физ. теорий позволила установить единство фундам. вз-ствий, выступавших в прежних теориях как независимые.

Физический энциклопедический словарь.— М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1983 .

(от лат. invarians, род. падеж invariantis - неизменяющийся) - фундам. физ. понятие, выражающее независимость физ. закономерностей от конкретных ситуаций, в к-рых они устанавливаются, и от способа описания этих ситуаций. Понятие И. применяется также к физ. величинам, значения к-рых не зависят от способа описания. калибровочной инвариантности происходит в терминах потенциалов поля (наблюдаемы их производные - напряжённости) и фаз волновых ф-ций (наблюдаемы квадраты их модулей - вероятности).Изменение условий наблюдения часто эквивалентно изменению способа описания явления: смена места и времени наблюдения - сдвигу начала отсчёта координат и времени, замена частиц на античастицы - операции зарядового сопряжения и т. п. Количественно это описывается преобразованиями физ. величин: координат, времени, потенциалов поля, волновых ф-ций и т. д. Как правило, каждая совокупность таких преобразований образует группу; её наз. группой И. или группой симметрии. В лагранжевом формализме (и гамилътоновом формализме )наличие непрерывных групп И. влечёт за собой важные физ. следствия: благодаря Нётер теореме каждой однопараметрич. группе И. соответствует сохраняющаяся физ. величина, являющаяся генератором группы. Принципы И. делятся на два осн. класса. И. первого класса, наиб. фундаментальная, характеризует геом. структуру пространства-времени. Однородность и изотропность пространства и однородность времени приводят к И. физ. законов относительно группы сдвигов координат и времени и пространств. вращений. Для изолиров. системы отсюда следует сохранение импульса, энергии и момента импульса. Эта И. является составной частью относительности принципа, содержащего дополнительно утверждение об И. относительно выбора инерц. системы отсчёта. В нерелятивистской теории полной группой И. является группа Галилея (см. Галилея принцип относительности), а релятивистская И.- это И. относительно преобразований Пуанкаре группы. И. первого класса универсальна н относится ко всем типам взаимодействий, к классич. и квантовой теории. В квантовой теории поля столь же универсальна СРТ-И. (см. Теорема СРТ), следующая из релятивистской инвариантности и причинности принципа. Ко второму классу относятся менее универсальные принципы И., характеризующие отд. типы взаимодействий. Таковы И. относительно калибровочных преобразований, унитарной симметрии, цветовой симметрии; такова И. эл.-магн. и сильного взаимодействий относительно обращения времени и пространственной инверсии;в теории элементарных частиц кажется перспективным выделение спец. типа взаимодействий, обладающего И. относительно преобразований суперсимметрии, и т. д. действия относительно преобразований групп симметрии. Чаще всего И. действия обеспечивается требованием И. лагранжиана, к-рое в значит. степени фиксирует его вид. Однако встречаются ситуации, когда И. действия обеспечена тем, что преобразование симметрии меняет лагранжиан на полную производную, а не просто оставляет его инвариантным. Аксиоматическая квантовая теория поля )и существенно используются при получении общих следствий теории (напр., теоремы СРТ, дисперсионных соотношений, перекрёстной симметрии И др.).При построении разл. объединённых теорий возникла концепция приближённой, или нарушенной, И. Обычно в таких теориях имеется параметр с размерностью массы (напр., разность масс частиц, участвующихв преобразованиях симметрии); при энергиях, много больших этого параметра, И. считается точной (см. Электрослабое взаимодействие, Великое объединение). Такой же характер имеет масштабная инвариантность, появляющаяся у амплитуд перехода при энергиях, много больших масс всех частиц, участвующих в р-ции. представлениям группы И. В этом случае сами величины и формулировка теории наз. ковариантными. При ковариантной формулировке теории любое её ур-ние не меняет своего вида при преобразованиях группы И., т. к. все его члены преобразуются согласованно. Это помогает, напр., фиксировать зависимость отдельных, заранее неизвестных членов ур-ния от остальных физ. величин, строить релятивистские обобщения нерелятивистских ф-л, перечислить возможные контрчлены в пвоцедуре перенормировки и т. п. Поэтому, начиная с А. Эйнштейна, для теоретич. физики характерно стремление к коварнантной формулировке любой физ. теории. Лит., Вигнер Е., Этюды о симметрии, пер. с англ., М., 1971. В. П. Павлов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Читайте также: