Энтропия и информация кратко

Обновлено: 30.06.2024

Файлы: 1 файл

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИИ 2 (Восстановлен).docx

2.1 Понятие энтропии и информации ………………. 5-6

2.2 Основа информационной теории ………………………. 7-12

2.3 Информационная энтропия……………………………….13-15

2.4 Свойства и эффективность………………………………..16- 17

4.Список используемой литературы………………………………………………23
Введение

Важнейшим шагом на пути постижения природы и механизмов антиэнтропийных процессов следует введение количественной меры информации. Первоначально эта мера предназначалась лишь для решения сугубо прикладных задач техники связи. Однако последующие исследования в области физики и биологии позволили выявить универсальные меры, предложенные К.Шенноном, позволяющие установить взаимосвязь между количеством информации и физической энтропией и в конечном счете определить сущность новой научной интерпретации понятия "информация" как меры структурной упорядоченности самых разнообразных по своей природе систем .
Используя метафору, можно сказать, что до введения в науку единой информационной количественной меры представленный в естественно-научных понятиях мир как бы "опирался на двух китов": энергию и вещество. "Третьим китом" оказалась теперь информация, участвующая во всех протекающих в мире процессах, начиная от микрочастиц, атомов и молекул и кончая функционированием сложнейших биологических и социальных систем.
Естественно, возникает вопрос: подтверждают или опровергают эволюционную парадигму происхождения жизни и биологических видов новейшие данные современной науки?
Для ответа на этот вопрос необходимо прежде всего уяснить, какие именно свойства и стороны многогранного понятия "информация" отражает та количественная мера, которую ввел в науку К.Шеннон.
Использование меры количества информации позволяет анализировать общие механизмы информационно-энтропийных взаимодействий, лежащих в основе всех самопроизвольно протекающих в окружающем мире процессов накопления информации, которые приводят к самоорганизации структуры систем.
Вместе с тем информационно-энтропийный анализ позволяет выявить и пробелы эволюционных концепций, представляющих собой не более чем несостоятельные попытки сведения к простым механизмам самоорганизации проблему происхождения жизни и биологических видов без учета того обстоятельства, что системы такого уровня сложности могут быть созданы лишь на основе той информации, которая изначально заложена в предшествующий их сотворению план.
Проводимые современной наукой исследования свойств информационных систем дают все основания утверждать, что все системы могут формироваться только согласно спускаемым с верхних иерархических уровней правилами, причем сами эти правила существовали раньше самих систем в форме изначального плана (идеи творения).

Понятие энтропии и информации

Энтропи́я (от греч. ἐντροπία — поворот, превращение) в естественных науках — мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).

Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.

где dS — приращение энтропии; δQ — минимальная теплота подведенная к системе; T — абсолютная температура процесса;

Информация (от лат. informatio, разъяснение, изложение, осведомленность) — общенаучное понятие, связанное с объективными свойствами материи и их отражением в человеческом сознании.

В современной науке рассматриваются два вида информации.

Объективная (первичная) информация - свойство материальных объектов и явлений (процессов) порождать многообразие состояний, которые посредством взаимодействий (фундаментальные взаимодействия) передаются другим объектам и запечатлеваются в их структуре.

Субъективная (семантическая,смысловая, вторичная) информация – смысловое содержание объективной информации об объектах и процессах материального мира, сформированное сознанием человека с помощью смысловых образов (слов, образов и ощущений) и зафиксированное на каком-либо материальном носителе.

В настоящее время не существует единого определения информации как научного термина. С точки зрения различных областей знания, данное понятие описывается своим специфическим набором признаков.

Основа информационной теории

В статистической физике с помощью вероятностной функции энтропии исследуются процессы, приводящие к термодинамическому равновесию, при котором все состояния молекул (их энергии, скорости) приближаются к равновероятным, а энтропия при этом стремится к максимальной величине.

Благодаря теории информации стало очевидно, что с помощью той же самой функции можно исследовать и такие далекие от состояния максимальной энтропии системы, как, например, письменный текст.
Еще один важный вывод заключается в том, что
с помощью вероятностной функции энтропии можно анализировать все стадии перехода системы от состояния полного хаоса, которому соответствуют равные значения вероятностей и максимальное значение энтропии, к состоянию предельной упорядоченности (жесткой детерминации), которому соответствует единственно возможное состояние ее элементов.

Данный вывод оказывается в равной мере справедливым для таких несходных по своей природе систем, как газы, кристаллы, письменные тексты, биологические организмы или сообщества и др.
При этом, если для газа или кристалла при вычислении энтропии сравнивается только микросостояние (т.е. состояние атомов и молекул) и макросостояние этих систем (т.е. газа или кристалла как целого), то для систем иной природы (биологических, интеллектуальных, социальных) вычисление энтропии может производится на том или ином произвольно выбранном уровне. При этом вычисляемое значение энтропии рассматриваемой системы и количество информации, характеризующей степень упорядоченности данной системы и равное разности между максимальным и реальным значением энтропии, будет зависеть от распределения вероятности состояний элементов нижележащего уровня, т.е. тех элементов, которые в своей совокупности образуют эти системы.
Другими словами,
количество сохраняемой в структуре системы информации пропорционально степени отклонения системы от состояния равновесия, обусловленного сохраняемым в структуре системы порядком.

Методы исчисления информации, предложенные Шенноном, позволяют выявить соотношение количества предсказуемой (то есть формируемой по определенным правилам) информации и количества той неожиданной информации, которую нельзя заранее предсказать.

Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределѐнность появления для некоторых букв меньше, чем для других. Если же учесть, что некоторые сочетания букв (в этом случае говорят об энтропии n-ого порядка, встречаются очень редко, то неопределѐнность ещѐ более уменьшается.

Для иллюстрации понятия информационной энтропии можно также прибегнуть к примеру из области термодинамической энтропии, получившему название демона Максвелла. Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу.

Информационная двоичная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле:

Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы. Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.

Определение по Шеннону

Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:

мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;
в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;
должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.

Поэтому функция энтропии H должна удовлетворять условиям:

определена и непрерывна для всех , где для всех и . (Нетрудно видеть, что эта функция зависит только от распределения вероятностей, но не от алфавита.)
Для целых положительных n, должно выполняться следующее неравенство:

Для целых положительных b_i, где , должно выполняться равенство:

Шеннон показал, [ источник? ] что единственная функция, удовлетворяющая этим требованиям, имеет вид:

где K — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии

Определение с помощью собственной информации

Также можно определить энтропию случайной величины, введя предварительно понятия распределения случайной величины X, имеющей конечное число значений:

и собственной информации:

Тогда энтропия определяется как:

От основания логарифма зависит единица измерения информации и энтропии: бит, трит, нат или хартли.

Свойства и эффективность

Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных.
Количество энтропии не всегда выражается целым числом бит.

Математические свойства

Неотрицательность: .
Ограниченность: . Равенство, если все элементы из X равновероятны.
Если независимы, то .
Энтропия — выпуклая вверх функция распределения вероятностей элементов.
Если имеют одинаковое распределение вероятностей элементов, то H(X) = H(Y).

Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — типичного набора или, на практике, — кодирования Хаффмана, кодирования Лемпеля — Зива — Велча или арифметического кодирования.

Вариации и обобщения

b-арная энтропия

В общем случае b-арная энтропия (где b равно 2, 3, …) источника с исходным алфавитом и дискретным распределением вероятности где p_i является вероятностью a_i (p_i = p(a_i)), определяется формулой:

Условная энтропия

Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (то есть, вероятности двухбуквенных сочетаний):

где i — это состояние, зависящее от предшествующего символа, и p_i(j) — это вероятность j при условии, что i был предыдущим символом.

Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других. Если же учесть, что некоторые сочетания букв (в этом случае говорят об энтропии n -ого порядка, см. ниже) встречаются очень редко, то неопределённость ещё более уменьшается.

Содержание

Формальные определения

Также можно определить энтропию случайной величины, введя предварительно понятия распределения случайной величины X , имеющей конечное число значений:

^n p_i=1" width="" height="" />

I(X) = − logP_X(X).

Тогда энтропия будет определяться как:

$H(X)=E(I(X))=-\sum_<i=1> ^n p(i)\log p(i).$

От основания логарифма зависит единица измерения информации и энтропии: бит, нат или хартли.

Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n ) рассчитывается по формуле:

$H(x)=-\sum_<i=1> ^np(i)\log_2 p(i).$

Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i , умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.

мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;
в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;
должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.

Шеннон показал, что единственная функция, удовлетворяющая этим требованиям, имеет вид:

$-K\sum_<i=1> ^np(i)\log_2 p(i),$

где K — константа (и в действительности нужна только для выбора единиц измерения).

В общем случае b -арная энтропия (где b равно 2, 3, …) источника =(S,\;P)" width="" height="" />
с исходным алфавитом " width="" height="" />
и дискретным распределением вероятности " width="" height="" />
где p_i является вероятностью a_i ( p_i = p(a_i) ) определяется формулой:

$H_b(\mathcal<S> )=-\sum_^n p_i\log_b p_i.$

Альтернативное определение

Другим способом определения функции энтропии H является доказательство, что H однозначно определена (как указано ранее), если и только если H удовлетворяет условиям:

Свойства

Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных.
Количество энтропии не всегда выражается целым числом бит.

Математические свойства

Эффективность

Из этого следует, что эффективность исходного алфавита с n символами может быть определена просто как равная его n -арной энтропии.

Вариации и обобщения

Условная энтропия

Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (то есть вероятности двухбуквенных сочетаний):

$H_1(\mathcal<S> )=-\sum_i p_i\sum_j p_i (j)\log_2 p_i(j),$

где i — это состояние, зависящее от предшествующего символа, и p_i(j) — это вероятность j , при условии, что i был предыдущим символом.

$p(b_j\mid a_i)$

Через частную и общую условные энтропии полностью описываются информационные потери при передаче данных в канале с помехами. Для этого применяются так называемые канальные матрицы. Так, для описания потерь со стороны источника (то есть известен посланный сигнал), рассматривают условную вероятность получения приёмником символа b_j при условии, что был отправлен символ a_i . При этом канальная матрица имеет следующий вид:

b₁	b₂	…	b_j	…	b_m
a₁	$p(b_1\mid a_1)$	$p(b_2\mid a_1)$	…	$p(b_j\mid a_1)$	…	$p(b_m\mid a_1)$
a₂	$p(b_1\mid a_2)$	$p(b_2\mid a_2)$	…	$p(b_j\mid a_2)$	…	$p(b_m\mid a_2)$
…	…	…	…	…	…	…
a_i	$p(b_1\mid a_i)$	$p(b_2\mid a_i)$	…	$p(b_j\mid a_i)$	…	$p(b_m\mid a_i)$
…	…	…	…	…	…	…
a_m	$p(b_1\mid a_m)$	$p(b_2\mid a_m)$	…	$p(b_j\mid a_m)$	…	$p(b_m\mid a_m)$

Очевидно, вероятности, расположенные по диагонали описывают вероятность правильного приёма, а сумма всех элементов столбца даст вероятность появления соответствующего символа на стороне приёмника — p(b_j) . Потери, приходящиеся на передаваемый сигнал a_i , описываются через частную условную энтропию:

$H(B\mid a_i)=-\sum_<j=1> ^m p(b_j\mid a_i)\log_2 p(b_j\mid a_i).$

Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:

$H(B\mid A)=\sum_i p(a_i)H(B\mid a_i).$

означает энтропию со стороны источника, аналогично рассматривается — энтропия со стороны приёмника: вместо всюду указывается (суммируя элементы строки можно получить p(a_i) , а элементы диагонали означают вероятность того, что был отправлен именно тот символ, который получен, то есть вероятность правильной передачи).

Взаимная энтропия

Взаимосвязь переданных и полученных сигналов описывается вероятностями совместных событий p(a_ib_j) , и для полного описания характеристик канала требуется только одна матрица:

p(a₁b₁)	p(a₁b₂)	…	p(a₁b_j)	…	p(a₁b_m)
p(a₂b₁)	p(a₂b₂)	…	p(a₂b_j)	…	p(a₂b_m)
…	…	…	…	…	…
p(a_ib₁)	p(a_ib₂)	…	p(a_ib_j)	…	p(a_ib_m)
…	…	…	…	…	…
p(a_mb₁)	p(a_mb₂)	…	p(a_mb_j)	…	p(a_mb_m)

Для более общего случая, когда описывается не канал, а просто взаимодействующие системы, матрица необязательно должна быть квадратной. Очевидно, сумма всех элементов столбца с номером j даст p(b_j) , сумма строки с номером i есть p(a_i) , а сумма всех элементов матрицы равна 1. Совместная вероятность p(a_ib_j) событий a_i и b_j вычисляется как произведение исходной и условной вероятности,

$p(a_ib_j)=p(a_i)p(b_j\mid a_i)=p(b_j)p(a_i\mid b_j).$

Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:

$H(A)=-\sum_i\left(\sum_j p(a_i b_j)\log\sum_j p(a_i b_j)\right),$
$H(B)=-\sum_j\left(\sum_i p(a_i b_j)\log\sum_i p(a_i b_j)\right).$

Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:

H(AB) = −	∑	∑	p(a_ib_j)logp(a_ib_j).
i	j

Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределённость на пару символов — отправленного и полученного. Путём несложных преобразований также получаем

$H(AB)=H(A)+H(B\mid A)=H(B)+H(A\mid B).$

Взаимная энтропия обладает свойством информационной полноты — из неё можно получить все рассматриваемые величины.

История

В 1948 году, исследуя проблему рациональной передачи информации через зашумлённый коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки двух основных направлений: теории информации, которая использует понятие вероятности и эргодическую теорию для изучения статистических характеристик данных и коммуникационных систем, и теории кодирования, в которой используются главным образом алгебраические и геометрические инструменты для разработки эффективных кодов.

Понятие было введено Клодом Элвудом Шенноном (1948) в его работе Математическая теория связи (A Mathematical Theory of Communication) [3] .

Содержание

Определение

$<\displaystyle \xi > Энтропия Шеннона дискретной с.в.$
, которая может принимать значения ,\ldots ,x_>" width="" height="" />
, равна величине

$<\displaystyle <\mathcal <H> >(\xi )=\operatorname (<\mathcal >(\xi ))=-\displaystyle ^p(x_)\log _p(x_),>>$

Характеризация

$<\displaystyle p_ Определим =\mathbf (\xi =x_)>$
и меру информационной энтропии >_(p_,\ldots ,p_)=<\mathcal >(\xi ).>" width="" height="" />

Непрерывность Мера должна быть переупорядочены: >_\left(p_,p_,\ldots \right)=<\mathcal >_\left(p_,p_,\ldots \right)>" width="" height="" />
и т.д. Максимум Мера должна быть максимальной, если все исходы одинаково вероятны (неопределённость является самой высокой, когда все возможные события равновероятны). >_(p_,\ldots ,p_)\leq <\mathcal >_\left(<\frac >,\ldots ,<\frac >\right)>" width="" height="" />
Для равновероятных событий энтропия должна увеличиваться с увеличением их числа: Аддитивность Количество энтропии не должно зависеть от того, как система событий разделена на части (подсистемы). Это последнее функциональное отношение характеризует энтропию системы с подсистемами и требует, чтобы энтропия системы могла быть вычислена через энтропии ее подсистем, если мы знаем, как подсистемы взаимодействуют с друг другом. Дан ансамбль из " width="" height="" />
равномерно распределённых элементов, которые произвольно разделены на " width="" height="" />
коробок (подсистем) с ,\ldots ,b_>" width="" height="" />
элементами соответственно; энтропия всего ансамбля должна быть равна сумме энтропии системы коробок и индивидуальных энтропий коробок, взвешенных с вероятностью обнаружения элемента в соответстувующей коробке. Для положительных целых чисел +\ldots +b_=n>" width="" height="" />
, >_\left(<\frac >,\ldots ,<\frac >\right)=<\mathcal >_\left(<\frac >,\ldots ,<\frac >\right)+\sum _^>>\,<\mathcal >_>\left(>>,\ldots ,>>\right).>" width="" height="" />
Выбор =1,\ldots ,b_=1>" width="" height="" />
подразумевает, что энтропия конкретного исхода равна нулю: >_\left(1\right)=0\,>" width="" height="" />

Можно показать, что любое определение энтропии, удовлетворяющее этим предположениям имеет форму

$<\displaystyle -K\sum _<i=1> ^p_\log p_\,\!>$

$<\displaystyle K> где$
— постоянная, соответствующая выбору единицы измерения.

Пояснения

Пример

Дальнейшие свойства

Увеличение энтропии Байеса — закон, согласно которому по мере увеличения выборки сравнения объектов А` для идентификации объекта А, индивидуальные особенности объекта А размываются по отношению к выборке, а идентификация становится бессмысленной. Другими словами с увеличение выборки у объекта А по отношению к ней увеличивается энтропия.

Считается, что закон был открыт эмпирически, до его математического доказательства британским математиком Томасом Байесом. В настоящее время в разных интерпретациях используется в кибернетике, информатике, теории систем, менеджменте и других науках. Некоторые математики и физики считают этот закон еще одним из начал термодинамики.

Пример. Если кто-то захочет установить личность человека, попавшего на видеокамеры, то процесс будет становится тем более бессмысленным, чем с большим количеством людей будет сравнен человек.

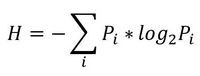
Итак, начнем с начала. Шенноном в 1963 г. было предложено понятие меры усредненной информативности испытания (непредсказуемости его исходов), которая учитывает вероятность отдельных исходов (до него был еще Хартли, но это опустим). Если энтропию измерять в битах, и взять основание 2, то получим формулу для энтропии Шеннона
, где Pi это вероятность наступления i-го исхода.

термодинамическая
алгоритмическая
информационная
дифференциальная
топологическая

Для того, чтобы немного обрисовать области применения энтропии к анализу данных, рассмотрим небольшую прикладную задачку из монографии [1] (которой нет в цифровом виде, и скорей всего не будет).

Пусть есть система, которая каждые 100 тактов переключается между несколькими состояниями и порождает сигнал x (рисунок 1.5), характеристики которого изменяются при переходе. Но какие — нам не известно.

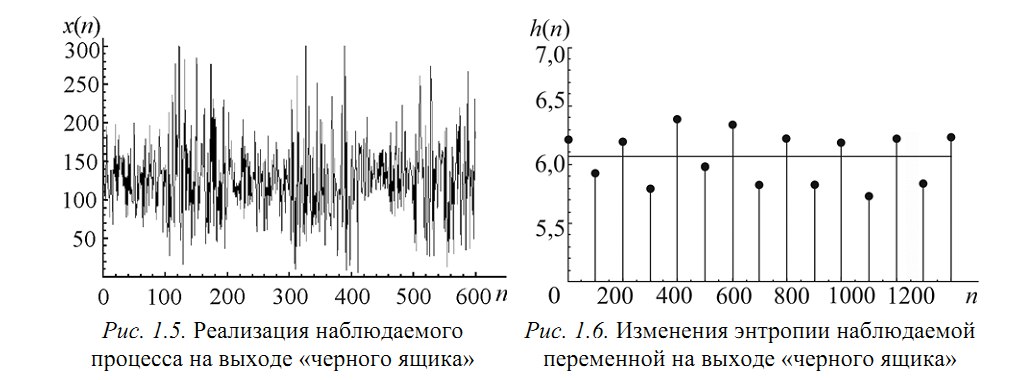
Теперь еще про одно занятное свойство энтропии — она позволяет оценить степень связности нескольких процессов. При наличии у них одинаковых источников мы говорим, что процессы связаны (например, если землетрясение фиксируют в разных точках Земли, то основная составляющая сигнала на датчиках общая). В таких случаях обычно применяют корреляционный анализ, однако он хорошо работает только для выявления линейных связей. В случае же нелинейных (порожденных временными задержками, например) предлагаем пользоваться энтропией.

Рассмотрим модель из 5ти скрытых переменных(их энтропия показана на рисунке ниже слева) и 3х наблюдаемых, которые генерируются как линейная сумма скрытых, взятых с временными сдвигами по схеме, показанной ниже справа. Числа-это коэффициенты и временные сдвиги (в отсчетах).

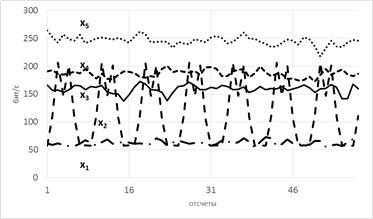
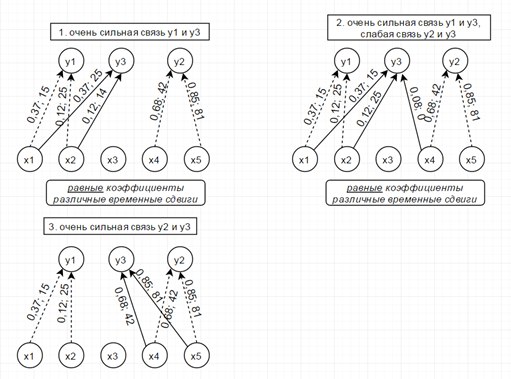
Так вот, фишка в том, что энтропия связных процессов сближается при усилении их связи. Черт побери, как это красиво-то!

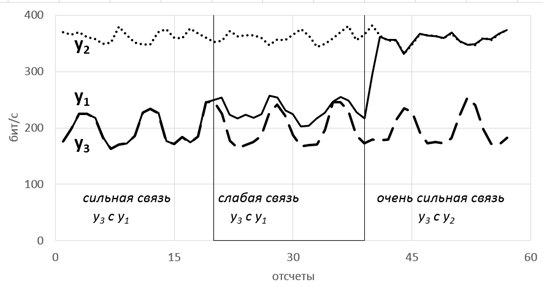
Такие радости позволяют вытащить практически из любых самых странных и хаотичных сигналов (особенно полезно в экономике и аналитике) дополнительные сведения. Мы их вытаскивали из электроэнцефалограммы, считая модную нынче Sample Entropy и вот какие картинки получили.

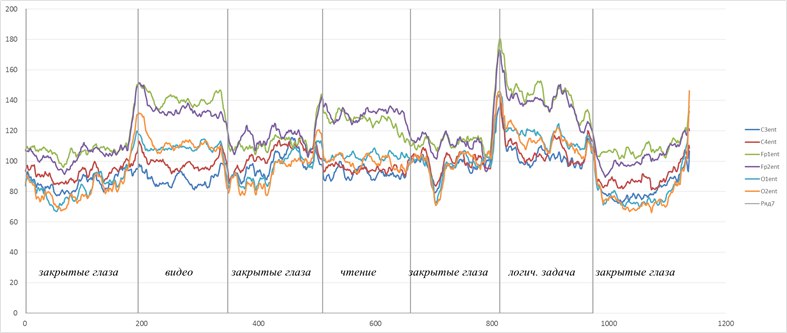
Можно видеть, что скачки энтропии соответствуют смене этапов эксперимента. На эту тему есть пара статей и уже защищена магистерская, так что если кому будут интересны подробности — с радостью поделюсь. А так по миру по энтропии ЭЭГ ищут уже давно разные вещи — стадии наркоза, сна, болезни Альцгеймера и Паркинсона, эффективность лечения от эпилепсии считают и тд. Но повторюсь-зачастую расчеты ведутся без учета поправочных коэффициентов и это грустно, так как воспроизводимость исследований под большим вопросом (что критично для науки, так то).

Резюмируя, остановлюсь на универсальности энтропийного аппарата и его действительной эффективности, если подходить ко всему с учетом подводных камней. Надеюсь, что после прочтения у вас зародится зерно уважения к великой и могучей силе Энтропии.

Читайте также:

Энтропия и информация кратко

Оглавление

Файлы: 1 файл

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИИ 2 (Восстановлен).docx

Определение по Шеннону

Определение с помощью собственной информации

Математические свойства

Вариации и обобщения

b-арная энтропия

Условная энтропия

Содержание

Формальные определения

Альтернативное определение

Свойства

Математические свойства

Эффективность

Вариации и обобщения

Условная энтропия

Взаимная энтропия

История

Содержание

Определение

Характеризация

Пояснения

Пример

Дальнейшие свойства