Случайные события и их вероятности конспект урока 11 класс

Обновлено: 04.07.2024

Испытанием называется осуществление определенных действий.

Событие- факт, который может произойти в результате испытания.

Любой результат испытания называется исходом.

Достоверным называют событие, которое в результате испытания обязательно произойдёт.

Невозможным называют событие, которое заведомо не произойдёт в результате испытания.

Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.

Если события не могут произойти одновременно в одном испытании, то события называются несовместными.

Противоположное событие происходит тогда, когда исходное событие А не происходит.

Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.

Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.

Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.

Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.

Равновозможные события - такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.

Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.

Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.

Основная литература:

Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. - 4-е изд. - М.: Просвещение, 1995. - 288 с.: ил. - ISBN 5-09-0066565-9. сс.242-261.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?

1) вынутый предмет окажется клубком

2) вынутый предмет окажется красным клубком

3) вынутый предмет окажется зеленым клубком

4) вынутый предмет не окажется клубком

Ответ: первое и третье.

1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.

Определение.

Испытанием называется осуществление определенных действий.

Под событием понимают любой факт, который может произойти в результате испытания.

Любой результат испытания называется исходом.

Достоверным называют событие, которое в результате испытания обязательно произойдёт.

Невозможным называют событие, которое заведомо не произойдёт в результате испытания.

События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).

Рассматривая приведенный пример, мы можем сформулировать следующие заключения.

2. Определим еще несколько важных понятий теории вероятностей

Определение

Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.

Например, при броске одной игральной кости пространство элементарных событий Ω= 1, w ₂, w ₃, w ₄, w ₅, w₆>, где w_i- выпадение i очков.

Если события не могут произойти одновременно в одном испытании, то события называются несовместными.

Простейшим примером несовместных событий является пара противоположных событий.

Противоположное событие происходит тогда, когда исходное событие А не происходит.

Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.

A – сдал экзамен по математике;
Ᾱ – не сдал экзамен по математике.

Определение.

Монету подбросили дважды. Укажите все элементарные события полной группы событий.

Элементарными событиями являются:

3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.

Определение.

Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.

Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Ее еще называют статистической вероятностью события.

Статистическая вероятность события рассчитывается опытным путем.

Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.

Это означает, что Вероятность рождения мальчика составляет 0,514.

1. Классическое определение вероятности применяется для равновозможных событий.

К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.

Например, при бросании игрального кубика события выпадения любого из очков равно возможны.

Рассмотрим произвольный эксперимент.

Согласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.

Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.

2 .Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.

Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.

Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:

Примеры и разбор решения заданий тренировочного модуля

Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?

Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:

9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;

10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.

Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.

Таким образом, чаще выпадает сумма 10.

Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.

Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.

Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.

В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Случайные события и их вероятности"

• вывести формулу вероятности суммы событий;

• вывести формулу вероятности произведения событий;

• вывести формулы Бернули и геометрической вероятности.

На прошлых уроках мы с вами рассматривали примеры решения простейших вероятностных задач, при этом каждый раз мы исследовали конкретную математическую модель.

Сегодня от решения простейших вероятностных задач мы перейдём к более сложным. И познакомимся с некоторыми инструментами для их решения.

Начнём с задачи.

При решении этой задачи мы применили формулу:

А так же узнали, что несовместными называют события, которые не могут произойти одновременно.

В свою очередь произведением двух событий А и Б называют событие, которое наступает тогда и только тогда, когда наступает и событие А, и событие Б.

На этом примере мы показали, что произведение событий А и Б связано с пересечением множеств, соответствующих событиям А и Б.

В 9 классе мы говорили о связи понятий теории вероятности и теории множеств.

Сумма вероятностей двух событий равна сумме вероятности произведения этих событий и вероятности суммы этих событий.

Это понятие одно из важнейших в теории вероятностей. И определение независимым событиям поможет дать правило умножения.

Определение.

События А и Б называют независимыми, если вероятность произведения этих событий (то есть их одновременного наступления) равна произведению вероятностей этих событий.

Вероятность суммы двух независимых событий равна разности суммы вероятностей этих событий и вероятности произведения этих событий.

Решим задачу.

Иногда проводят серию одинаковых испытаний и находят вероятность наступления того или иного события.

Определение.

Сумма противоположных событий равна одному.

Теорема Бернулли.

Эта теорема очень важна. Применим её при решении задачи.

Запишем ещё одну теорему.

Например, при эн большем либо равном двум тысячам с вероятностью, большей чем 99%, можно утверждать, что абсолютная погрешность разности частоты и вероятности такого приближённого равенства будет меньше 0,03.

Поэтому при социологических опросах достаточно бывает опросить около 2000 случайно выбранных людей.

Допустим, 520 из них положительно ответили на заданный вопрос. Тогда:

И практически достоверно, что для любого большего числа опрошенных такая частота будет находиться в пределах от двадцати трёх сотых до двадцати девяти сотых.

Это явление называют явлением статистической устойчивости.

Вспомним уже знакомое вам классическое определение вероятности, оно применимо к испытаниям с конечным числом исходов.

Однако часто встречаются испытания с бесконечным числом исходов. В таких случаях прибегают к геометрической вероятности.

Рассмотрим пример.

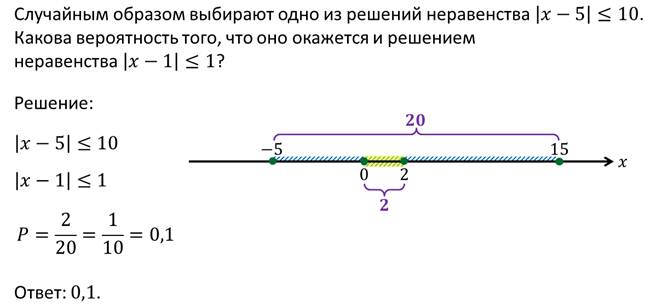
Можем сформулировать общее правило для нахождения геометрической вероятности.

Аналогично поступают и с множествами на плоскости, и с пространственными множествами. Но в этих случаях длину заменяют на площадь и объём соответственно.

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

Тема: Случайное событие. Вероятность события.

Цель урока : формировать умение применять формулу классической вероятности для подсчета вероятностей случайных событий;

Развивать память, внимание;

Воспитывать аккуратность, настойчивость.

Ожидаемые результаты: обучающиеся должны знать формулу классической вероятности и уметь применять ее при решении задач

Тип урока: комбинированный

I. ОРГАНИЗАЦИОННЫЙ ЭТАП

II. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ; АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ

Обучающиеся с места комментируют выполнение заданий среднего и достаточного уровней, задание высокого уровня разбирают более подробно.

ü Графический диктант

Обучающиеся записывают в тетради ответы, пользуясь символами (да ∩, нет __ ), а затем осуществляют самопроверку по ключу ответу.

4) Вероятность того, что у простого числа всего два делителя, равна 0;

5) Вероятность выбрать четное число среди делителей 15 равна

6) Вероятность выпадания нечетного числа при подбрасывании одного кубика равна

Ключ-ответ : ∩∩∩__ __ __

III. ФОРМУЛИРОВАНИЕ ТЕМЫ, ЦЕЛИ И ЗАДАЧ УРОКА; МОТИВАЦИЯ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ

Уже в каменном веке понимали, что вероятность победы над зверем больше у 15-ти воинов, чем у 9-ти. Но тогда наши предки были еще очень далеки от теории вероятностей. С приобретением опыта она все чаще старались планировать случайные события, классифицировать их исход. Так люди заметили, что случайностями часто управляют объективные закономерности.

IV. ОСМЫСЛЕНИЕ НОВОГО МАТЕРИАЛА

ü Коллективное решение задач под руководством учителя

1. Подкидывают два ‘кубика. Найдите вероятность следующих событий:

Решение. Так как одновременно подкидывают два кубика, то всего n =36 вариантов. Из них событию А благоприятствуют следующие: 2+6=8; 6+2=8; 5+3=8; 4+4=8, то есть m =5. Значит, P ( A ) = . Событию В благоприятствуют два события: 4∙2=8 и 2∙4=8.Значит, Р(В) = В. Событию С благоприятствуют следующие события: 1+1=2>1∙1; 1+2=3>1∙2=2; 2+1=3>2∙1; 4+1=5>4∙1; 1+4>1∙4; 1+3>1∙3; 8+1>3∙1; 5+1>5∙1; 1+5>1∙5;

6+1>6∙1; 1+6>1∙6, то есть m =11. Значит, Р(С) =

2. Из набора для игры в домино, состоящего из 28 костей, наугад взяли одну кость. Это оказался не дубль. Найдите вероятность след ующих событий:

Решение . В наборе семь дублей. Если взяли одну кость, то осталось 27 костей. Тогда вероятность события А: Р(А) = события В: Р(В) =

Обучающиеся объединяются в малые группы для решения задачи.

Задача. Куб, все грани которого окрашены, разрезали на 27 равных кубиков. Найдите вероятность того, что взятый наугад кубик имеет: а) три окрашенные грани; б) две окрашенные грани; в) одну окрашенную грань; г) не имеет окрашенных граней.

Решение . а) Три окрашенные грани могут иметь только кубики, находящиеся в вершинах куба. У куба 8 вершин, всего 27 вариантов, значит, Р(А) = б) Две окрашенные грани имеют кубики, находящиеся в середине каждого ребра. У куба всего 12 ребер, значит Р(В) = в)Одну окрашенную грань имеют кубики, находящиеся в середине каждой грани. У куба 6 граней, значит, Р(С) = г) Ни одной грани не окрашено у кубика, который находится внутри куба. Такой кубик всего один, значит, Р( D ) =

V. ПОДВЕДЕНИЕ ИТОГОВ УРОКА

Учитель обращает внимание обучающихся на то, что в некоторых задачах подсчет благоприятных вариантов осуществлялся простым перебором всевозможных вариантов, что занимает довольно много времени. Иногда удобнее пользоваться специальными формулами — они будут изучены в дальнейшем.

Цель урока: рассмотреть простейшие понятия теории вероятностей.

Задачи урока:

образовательные: научить в процессе реальной ситуации определять достоверные, невозможные, равновероятностные, совместные и несовместные события; научить решать задачи из жизни;

воспитательные: воспитание умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, настойчивости в достижении цели и заинтересованности в конечном результате труда;

развивающие: развитие умения анализировать, обобщать изучаемые факты, выделять и сравнивать существенные признаки, выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия; контроль и оценка процесса и результатов деятельности.

I. Организационный момент.

II. Актуализация опорных знаний. Проверка домашнего задания.

Задание 1.Для каждого из следующих опытов определить, какие события являются достоверными, случайными, невозможными.

Опыт 1. В группе 25 студентов, есть юноши и есть девушки.

случайным образом выбранный студент – девушка;

у двоих студентов день рождения 31 февраля;

всем студентам группы больше 13 лет.

Опыт 2. При бросании трех игральных костей.

сумма выпавших на трех костях очков меньше 15;

на первой кости выпало 2 очка, на второй – 3 очка, на третьей – 6 очков;

сумма выпавших на трех костях очков равна 19.

Задание 2. Найти пары совместных и несовместных событий, связанных с однократным бросанием игральной кости.

выпало нечетное число очков,

выпало менее 4 очков,

выпало четное число очков,

выпало более 4 очков.

III. Изучение нового материала

Вероятностью события называется отношение числа элементарных исходов опыта, благоприятствующих данному событию, к числу всех равновозможных элементарных исходов опыта:

, где А – событие, m - число благоприятствующих исходов опыта,

n - число всех равновозможных элементарных исходов опыта,

P(A) - вероятность наступления события А.

Свойства вероятностей события.

Если А – событие, то .

Если А – достоверное событие, то P(A) = 1.

Если А – невозможное событие, то P(A) = 0.

Если А – случайное событие, то

Если А и - противоположные события, то

Если А₁, А₂, А₃, . . . , А_n – полная группа событий, то

IV. Закрепление знаний. Решение задач на вычисление вероятности слу чайного события.

В урне находится 15 белых, 5 красных и 10 чёрных шаров. Наугад извлекается 1 шар, найти вероятность того, что он будет: а) белым, б) не чёрным.

Ответ:

Задача 2. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность Р(А) того, что взятый наудачу подшипник окажется стандартным.

Решение. Число стандартных подшипников равно 1000 – 30 = 970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из n = 1000 равновероятных исходов, из которых событию А благоприятствуют m = 970 исходов.

Поэтому Р(А) = Ответ: 0,97.

Задача 3. Найдем вероятность того, что при одном бросании игральной кости (кубика) выпадает: а) три очка; б) число очков, кратное трем; в) число очков больше трех; г) число очков, не кратное трем.

Решение. Всего имеется n=6 возможных исходов: выпадение 1,2,3,4,5,6 очков. Считаем, что эти исходы равновозможные.

а) Только при одном из исходов m=1 происходит интересующее нас

событие А – выпадение трех очков. Вероятность этого события Р(А) = .

б) При двух исходах m = 2 происходит событие B: выпадение числа очков кратных трем: выпадение или трех или шести очков. Вероятность такого события Р(B) = .

в) При трех исходах m = 3 происходит событие C: выпадение числа очков больше трех: выпадение четырех, пяти или шести очков. Вероятность этого события Р(C) = .

г) Из шести возможных выпавших чисел четыре (1, 2, 4 и 5) не кратны трем, а остальные два (3 и 6) делятся на три. Значит, интересующее нас событие D,

наступает в четырех случаях, т.е. m = 4. Вероятность такого события: P(D)= .

Ответ: а) ; б) ; в) ; г) .

Задача 4. В среднем из 1000 аккумуляторов, поступивших в продажу, 6 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.

Решение. Элементарный исход – случайно выбранный аккумулятор. Поэто- му n = 1000.

Событию А = благоприятствуют 1000 – 6 = 994 исхода.

Тогда P(A)=

Эту задачу можно решить с помощью формулы вероятности противоположного события = . Тогда m=6.

Имеем P( Значит, P(A) = 1- P( )=1 – 0,006 = 0,994.

V. Итоги урока

Ученики проговаривают, что нового узнали на уроке. Учитель оценивает работу ребят. При выходе из кабинета каждый ученик выбирает прямоугольник по цвету, соответствующему надписями “всё понятно и усвоено”, “трудно и не всё понятно”, “не понятно и не усвоено”, и опускает в соответствующий конверт.

Читайте также: