Умножение векторов определение кратко

Обновлено: 04.07.2024

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.

Это одна из основных операций над векторами в векторной алгебре. Вектор, в отличие от обычного отрезка, имеет не только длину, но и направление в пространстве.

Основные типы перемножения векторов

В математике есть два основных вида умножения векторов: скалярное и векторное. Результатом первого является число, результатом второго — вектор. Оба произведения применяются к двум векторам. Также выделяют смешанное произведение векторов, которое является комбинацией двух вышеописанных. Оно применяется, когда необходимо узнать результат умножения трех векторов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Скалярное

Скалярным произведением двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Длина вектора является его модулем.

Записывается скалярное произведение двумя способами: $ (\overline a,\;\overline b) $ или $ \overline a\cdot\overline b.$

Алгебраические свойства скалярного произведения

Перестановочность. Произведение не меняется от перемены мест множителей: $\overline a\cdot\overline b=\overline b\cdot\overline a.$
Сочетательность относительно числа. Умножение одного из векторов на число равносильно умножению обоих векторов на это число: $(\lambda\overline a)\cdot\overline b=\lambda(\overline a\cdot\overline b)(\lambda\overline a)\cdot(\mu\overline b)=(\lambda\mu)(\overline a\cdot\overline b).$
Распределительный закон. Скалярное произведение суммы двух векторов на третий равносильно сумме скалярных произведений этих векторов на третий вектор: $(\overline a+\overline b)\cdot\overline c=\overline a\cdot\overline c+\overline b\cdot\overline c.$

Таким образом, при выполнении алгебраических действий, связанных со скалярным произведением, с векторами можно обращаться как с числами.

Геометрические свойства скалярного умножения

Скалярное произведение вектора на него же равняется квадрату его модуля: $\overline a\cdot\overline a=\overline a^2=\overline<\left|a\right|>\cdot\overline<\left|a\right|>\cdot\cos\left(0\right)=\left|\overline a^2\right|.$
Если угол между векторами острый (меньше $90^\circ$ ), то скалярное произведение этих векторов больше нуля.
Если угол между векторами тупой (больше $90^\circ$ ), то их скалярное произведение меньше нуля.
Если вектора перпендикулярны (угол равен $90^\circ$ ), то их скалярное произведение будет равняться нулю.
Если координаты перемножаемых векторов известны, то их скалярное произведение будет равняться сумме произведений соответствующих координат: $ \overline a\cdot\overline b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z.$

Геометрический смысл

Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию второго вектора на первый.

$\overline a\cdot\overline b=\left|\overline a\right|\cdot пр_\overline a\overline b=\overline<\left|b\right|>\cdot пр_\overline b\overline a$

Физический смысл

Скалярное произведение применяется для расчета работы, выполняемой при перемещении материальной точки вдоль вектора $\overline s$ под действием силы $\overline F$ , приложенной под некоторым углом $\varphi.$

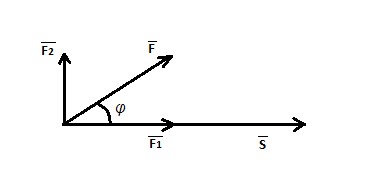
Рисунок 1. Физический смысл скалярного произведения

Силу $\overline F$ необходимо разложить на ортогональные компоненты $\overline$ и $\overline.$ Тогда $\overline$ будет являться проекцией силы $\overline F$ на вектор $\overline s:$

В свою очередь, работа A вычисляется по формуле:

Соединив данные формулы получим:

$A=\left|\overline F\right|\cdot\left|\overline S\right|\cdot\cos\left(\varphi\right),$

что является скалярным произведением векторов $\overline F$ и $\overline s:$

$A=\overline F\cdot\overline S.$

Векторное

Векторным произведением векторов \overline a и \overline b называют перпендикулярный им вектор \overline c из правой тройки, модуль которого равняется произведению модулей векторов \overline a и \overline b на синус угла между ними.

Упорядоченная тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого ко второму совершается против часовой стрелки. В противном случае такая тройка называется левой.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Векторное произведение может выражаться в записи двумя способами: $\overline a\times\overline b$ и $\lbrack\overline a,\overline b\rbrack.$

Алгебраические свойства

Антиперестановочность. В отличие от скалярного произведения, в векторном при перемене мест множителей знак меняется на противоположный: $\overline a\times\overline b=-(\overline b\times\overline a)$
Сочетательность относительно числа. Как и в случае со скалярным умножением, произведение числа на один из векторов равняется произведению его на другой или на оба вектора: $(\lambda\overline a)\times\overline b=\overline a\times(\lambda\overline b)=\lambda(\overline a\times\overline b).$
Распределительный закон. Векторное произведение суммы двух векторов на третий равносильно сумме векторных произведений этих векторов на третий вектор: $(\overline a+\overline b)\times\overline c=\overline a\times\overline c+\overline b\times\overline c.$

Из этого следует, что при выполнении алгебраических действий, связанных с векторным произведением, скобки можно раскрывать так же, как при работе с числами, с поправкой на правило антиперестановочности.

Геометрические свойства

Если вектора $\overline a$ и $\overline b$ параллельны, то их векторное произведение равняется нулю.
Векторное произведение векторов с известными координатами выражается в матричном виде: $\overline a\times\overline b=\begini&j&k\\a_x&a_y&a_z\\b_x&b_y&b_z\end=\left(\begina_y&a_z\\b_y&b_z\end;\;-\begina_x&a_z\\b_x&b_z\end;\;\begina_x&a_y\\b_x&b_y\end\right).$

Геометрический смысл

Модуль векторного произведения двух векторов равняется площади параллелограмма, сторонами которого являются эти вектора.

Рисунок 2. Геометрический смысл векторного произведения

Из определения векторного умножения следует, что модуль полученного вектора равняется произведению модулей исходных векторов на синус угла между ними:

Площадь параллелограмма вычисляется так:

$S=\left|\overline a\right|\cdot h, где h=\left|\overline b\right|\cdot\sin\left(\varphi\right).$

Таким образом, получаем:

Отсюда следует формула для площади треугольника:

$S_\bigtriangleup=\frac12\left|\overline a\times\overline b\right|$

Физический смысл

В физике векторное произведение применяется для расчета момента силы, приложенной к одной точке относительно другой:

$\overline M=\overline\times\overline F$

Смешанное умножение векторов

Фактически, смешанное произведение векторов представляется как скалярное умножение одного вектора на векторное произведение двух других. Результатом смешанного произведения является число.

Свойства смешанного умножения

$(\overline a\times\overline b)\cdot\overline c=\overline a\cdot(\overline b\times\overline c)=\overline a\cdot\overline b\cdot\overline c.$
Если $\overline a\cdot\overline b\cdot\overline c$ больше нуля, тройка векторов — правая.
Если $ \overline a\cdot\overline b\cdot\overline c$ меньше нуля, тройка векторов — левая.
Если вектора $\overline a, \overline b$ и $\overline c$ компланарны, то их смешанное произведение равняется нулю.

Геометрический смысл

Если вектора \overline a, \overline b и \overline c не компланарны, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах. Число будет положительным, если тройка векторов правая, и отрицательным, если тройка левая.

$V_=\overline a\cdot\overline b\cdot\overline c$

Следствием этого является формула нахождения объема пирамиды:

$V_=\frac16\left(\overline a\cdot\overline b\cdot\overline c\right)$

Произведение векторов, примеры и решения

Задача №1

Даны вектора $\overline a=(-1,\;0,\;3) и \overline b=(2,\;-3,\;1).$

Найти их скалярное произведение.

Решение

Возьмем формулу скалярного произведения для векторов с известными координатами:

$\overline a\cdot\overline b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z$ и подставим имеющиеся значения:

$\overline a\cdot\overline b=(-1)\cdot2+0\cdot(-3)+3\cdot1=1$

Задача №2

Найти площадь треугольника с известными координатами угловых точек

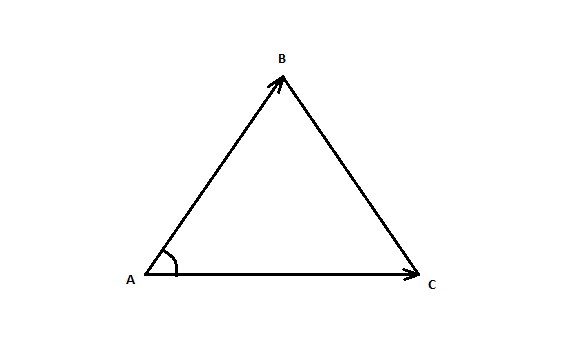
Решение

Для решения этой простейшей задачи из геометрии воспользуемся следствием геометрического смысла векторного произведения:

$S_\bigtriangleup=\frac12\left|\overline a\times\overline b\right|$

В данном случае треугольник построен на векторах $ \overline$ и $\overline$ . Чтобы рассчитать их координаты, необходимо вычесть из координат конечной точки координаты начальной:

Векторное произведение векторов с известными координатами выполняется в матричном виде:

Подставляем значения векторов $ \overline$ и $\overline$ в матрицу и производим вычисления:

Подставляем полученное значение в формулу вычисления площади треугольника, учитывая, что в ней фигурирует модуль произведения:

Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a → , b → , c → в трехмерном пространстве.

Отложим для начала векторы a → , b → , c → от одной точки. Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a → , b → , c → называется правой, если по часовой стрелке – левой.

Далее возьмем два не коллинеарных вектора a → и b → . Отложим затем от точки A векторы A B → = a → и A C → = b → . Построим вектор A D → = c → , который одновременно перпендикулярный одновременно и A B → и A C → . Таким образом, при построении самого вектора A D → = c → мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

Упорядоченная тройка векторов a → , b → , c → может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.

Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

если векторы a → и b → коллинеарны, он будет нулевым;
он будет перпендикулярен и вектору a → и вектору b → т.е. ∠ a → c → = ∠ b → c → = π 2 ;
его длина определяется по формуле: c → = a → · b → · sin ∠ a → , b → ;
тройка векторов a → , b → , c → имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a → и b → имеет следущее обозначение: a → × b → .

Координаты векторного произведения

Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a → = ( a x ; a y ; a z ) и b → = ( b x ; b y ; b z ) называют вектор c → = a → × b → = ( a y · b z - a z · b y ) · i → + ( a z · b x - a x · b z ) · j → + ( a x · b y - a y · b x ) · k → , где i → , j → , k → являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i → , j → , k → , вторая строка содержит координаты вектора a → , а третья – координаты вектора b → в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Разложив данный определитель по элементам первой строки, получим равенство: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = ( a y · b z - a z · b y ) · i → + ( a z · b x - a x · b z ) · j → + ( a x · b y - a y · b x ) · k →

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы c → = a → × b → = i → j → k → a x a y a z b x b y b z , то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

антикоммутативность a → × b → = - b → × a → ;
дистрибутивность a ( 1 ) → + a ( 2 ) → × b = a ( 1 ) → × b → + a ( 2 ) → × b → или a → × b ( 1 ) → + b ( 2 ) → = a → × b ( 1 ) → + a → × b ( 2 ) → ;
ассоциативность λ · a → × b → = λ · a → × b → или a → × ( λ · b → ) = λ · a → × b → , где λ - произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

По определению a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z . А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулой c → = a → · b → · sin ∠ a → , b → .

Найдите длину векторного произведения векторов a → и b → , если известно a → = 3 , b → = 5 , ∠ a → , b → = π 4 .

С помощью определения длины векторного произведения векторов a → и b → решим данную задач: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Ответ: 15 2 2 .

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a → = ( a x ; a y ; a z ) и b → = ( b x ; b y ; b z ) .

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a → и b → , а их разложения по координатным векторам вида b → = b x · i → + b y · j → + b z · k → и c → = a → × b → = ( a y · b z - a z · b y ) · i → + ( a z · b x - a x · b z ) · j → + ( a x · b y - a y · b x ) · k → , или векторы a → и b → могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

В прямоугольной системе координат заданы два вектора a → = ( 2 ; 1 ; - 3 ) , b → = ( 0 ; - 1 ; 1 ) . Найдите их векторное произведение.

По второму определению найдем векторное произведение двух векторов в заданных координатах: a → × b → = ( a y · b z - a z · b y ) · i → + ( a z · b x - a x · b z ) · j → + ( a x · b y - a y · b x ) · k → = = ( 1 · 1 - ( - 3 ) · ( - 1 ) ) · i → + ( ( - 3 ) · 0 - 2 · 1 ) · j → + ( 2 · ( - 1 ) - 1 · 0 ) · k → = = - 2 i → - 2 j → - 2 k → .

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Ответ: a → × b → = - 2 i → - 2 j → - 2 k → .

Найдите длину векторного произведения векторов i → - j → и i → + j → + k → , где i → , j → , k → - орты прямоугольной декартовой системы координат.

Для начала найдем координаты заданного векторного произведения i → - j → × i → + j → + k → в данной прямоугольной системе координат.

Известно, что векторы i → - j → и i → + j → + k → имеют координаты ( 1 ; - 1 ; 0 ) и ( 1 ; 1 ; 1 ) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Следовательно, векторное произведение i → - j → × i → + j → + k → имеет координаты ( - 1 ; - 1 ; 2 ) в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Ответ: i → - j → × i → + j → + k → = 6 . .

В прямоугольной декартовой системе координат заданы координаты трех точек A ( 1 , 0 , 1 ) , B ( 0 , 2 , 3 ) , C ( 1 , 4 , 2 ) . Найдите какой-нибудь вектор, перпендикулярный A B → и A C → одновременно.

Векторы A B → и A C → имеют следующие координаты ( - 1 ; 2 ; 2 ) и ( 0 ; 4 ; 1 ) соответственно. Найдя векторное произведение векторов A B → и A C → , очевидно, что оно является перпендикулярным вектором по определению и к A B → и к A C → , то есть, является решением нашей задачи. Найдем его A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Ответ: - 6 i → + j → - 4 k → . - один из перпендикулярных векторов.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Векторы a → и b → перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения 3 · a → - b → × a → - 2 · b → = 3 · a → × a → - 2 · b → + - b → × a → - 2 · b → = = 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

По свойству дистрибутивности векторного произведения мы можем записать 3 · a → - b → × a → - 2 · b → = 3 · a → × a → - 2 · b → + - b → × a → - 2 · b → = = 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b →

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · ( - 2 ) · a → × b → + ( - 1 ) · b → × a → + ( - 1 ) · ( - 2 ) · b → × b → = = 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b →

Векторные произведения a → × a → и b → × b → равны 0, так как a → × a → = a → · a → · sin 0 = 0 и b → × b → = b → · b → · sin 0 = 0 , тогда 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .

Из антикоммутативности векторного произведения следует - 6 · a → × b → - b → × a → = - 6 · a → × b → - ( - 1 ) · a → × b → = - 5 · a → × b → . .

Воспользовавшись свойствами векторного произведения, получаем равенство 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

По условию векторы a → и b → перпендикулярны, то есть угол между ними равен π 2 . Теперь остается лишь подставить найденные значения в соответствующие формулы: 3 · a → - b → × a → - 2 · b → = - 5 · a → × b → = = 5 · a → × b → = 5 · a → · b → · sin ( a → , b → ) = 5 · 3 · 4 · sin π 2 = 60 .

Ответ: 3 · a → - b → × a → - 2 · b → = 60 .

Геометрический смысл векторного произведения

Длина векторного произведения векторов по орпеделению равна a → × b → = a → · b → · sin ∠ a → , b → . Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма - удвоенного треугольника, а именно произведению сторон в виде векторов a → и b → , отложенные от одной точки, на синус угла между ними sin ∠ a → , b → .

Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.

Под моментом силы F → , приложенной к точке B , относительно точки A будем понимать следующее векторное произведение A B → × F → .

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение векторного произведения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Координаты векторного произведения

Рассмотрим векторное произведение векторов в координатах.

Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

→i, →j, →k — координатные векторы.

Это определение показывает нам векторное произведение в координатной форме.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:

Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

, где λ произвольное действительное число.

Для большей ясности докажем свойство антикоммутативности векторного произведения.

Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому

что доказывает свойство антикоммутативности векторного произведения.

Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.

Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Примеры решения задач

Пример 1

а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:

Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.

б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:

Пример 2

Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.

По условию снова нужно найти длину векторного произведения. Используем нашу формулу:

Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.

Пример 3

Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.

Сначала найдём векторы:

Затем векторное произведение:

Вычислим его длину:

Подставим данные в формулы площадей параллелограмма и треугольника:

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна

А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].

Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим.

Определение

Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:

$\mathbf c = \left[ \mathbf a \mathbf b \right] = \left[ \mathbf a,\; \mathbf b \right] = \mathbf a \times \mathbf b$

В различных учебных заведениях определение векторного произведения даётся по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах. А далее выводится данное выше определение.

Свойства

Геометрические свойства векторного произведения

Алгебраические свойства векторного произведения

Выражение для векторного произведения в декартовых координатах

Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе

$\mathbf a = (a_x,\; a_y,\; a_z)$
$\mathbf b = (b_x,\; b_y,\; b_z)$

то их векторное произведение имеет вид

$[ \mathbf a,\; \mathbf b ] = (a_y b_z - a_z b_y,\; a_z b_x - a_x b_z,\; a_x b_y - a_y b_x).$

Для запоминания этой формулы удобно использовать определитель:

$[ \mathbf a,\; \mathbf b ] = \begin \mathbf i & \mathbf j & \mathbf k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end$

$[ \mathbf a,\; \mathbf b ]_i = \sum_<j,k=1> ^3 \varepsilon_ a_j b_k,$

$\varepsilon_ где$
— символ Леви-Чивиты.

Обобщения

Кватернионы

Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.

Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов i , j и k . Если представить вектор как кватернион a₁i + a₂j + a₃k , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.

Преобразование к матричной форме

Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:

= [\mathbf]_ \mathbf = \begin\,0&\!-a_3&\,\,a_2\\ \,\,a_3&0&\!-a_1\\-a_2&\,\,a_1&\,0\end\beginb_1\\b_2\\b_3\end" width="" height="" />
\times \mathbf = \mathbf^T [\mathbf]_ = \beginb_1&b_2&b_3\end\begin\,0&\!-a_3&\,\,\,a_2\\\,\,\,a_3&\,0&\!-a_1\\-a_2&\,\,a_1&\,0\end" width="" height="" />

$[\mathbf]_ <\times> \stackrel \begin\,\,0&\!-a_3&\,\,\,a_2\\\,\,\,a_3&0&\!-a_1\\\!-a_2&\,\,a_1&\,\,0\end$

$\mathbf$

Пусть равен векторному произведению:

$\mathbf= \mathbf <c> \times \mathbf$

$[\mathbf]_ <\times> = (\mathbf\mathbf^T)^T - \mathbf\mathbf^T.$

Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь n(n − 1) / 2 независимых компонент в n -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.

С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).

Из общих свойств векторного произведения следует, что

\, \mathbf = \mathbf " width="" height="" />
и \, [\mathbf]_ = \mathbf " width="" height="" />

$[\mathbf]_ <\times> а так как$
кососимметрична, то

$\mathbf ^ \, [\mathbf]_ \, \mathbf = 0.$

Распространение на матрицы

В 3-хмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу A как столбец векторов, тогда

\vec a_1\\\vec a_2\\\vec a_3\end \times \vec b = \begin\vec a_1 \times \vec b \\\vec a_2 \times \vec b \\\vec a_3 \times \vec b \end" width="" height="" />
\vec a_1\\\vec a_2\\\vec a_3\end \cdot \vec b = \begin\vec a_1 \cdot \vec b \\\vec a_2 \cdot \vec b \\\vec a_3 \cdot \vec b \end" width="" height="" />

Умножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( A — матрица, , — векторы):

$A \cdot (\vec x \times \vec y) = (A \times \vec x) \cdot \vec y$
$A \times (\vec x \times \vec y) = \vec x (A \cdot \vec y)- \vec y (A \cdot \vec x)$

После этого можно изменить форму записи для векторного произведения:

$\vec x \times \vec y = E \cdot (\vec x \times \vec y) = (E \times \vec x)\cdot \vec y$

$\int\limits_<\Sigma> \operatorname\, \mathbf \, \mathbf = \int\limits_ <\partial\Sigma>\mathbf\cdot\, d \mathbf,$

где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:

\operatorname\, u \times \, \mathbf = \int\limits_ <\partial\Sigma>u\, d \mathbf, " width="" height="" />
\left[ \mathbf; \left[ \nabla; \vec a \right] \right] = \int\limits_ <\partial\Sigma>\vec a \times d \mathbf. " width="" height="" />

Размерности, не равные трём

Пусть D — размерность пространства.

$\mathbb Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение ^D \times \mathbb^D \to \mathbb^D$
, можно ввести только для размерности 3.

$\varepsilon_<i_1 i_2 i_3 \ldots i_D> Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D -мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты$
с D индексами, можно явно записать такое (D − 1) -валентное векторное произведение как

Такое обобщение дает гиперплощадь размерности (D − 1) .

Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при D 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:

$\ P_<ij> (\mathbf) = a_i b_j - a_j b_i$
.

Эта конструкция называется внешним произведением.

Для двумерного случая эта операция называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат можно отождествить с псевдоскаляром.

Алгебра Ли векторов

Векторное произведение вводит на ^3" width="" height="" />
структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам -- антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.

Определение. Векторным произведением вектора a на вектор b называется вектор c , длина которого численно равна площади параллелограмма построенного на векторах a и b , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).

рис. 1

Формулы вычисления векторного произведения векторов

Векторное произведение двух векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z > в декартовой системе координат - это вектор, значение которого можно вычислить, используя следующие формулы:

Свойства векторного произведения векторов

Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:

Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:

Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.

Примеры задач на вычисления векторного произведения векторов

= i (-4 - 3) - j (-2 - 6) + k (1 - 4) = -7 i + 8 j - 3 k =

Решение: Найдем векторное произведение этих векторов:

= i (-2 + 2) - j (1 + 4) + k (-1 - 4) = -5 j - 5 k =

Из свойств векторного произведения:

SΔ = 1 2 | a × b | = 1 2 √ 0 2 + 5 2 + 5 2 = 1 2 √ 25 + 25 = 1 2 √ 50 = 5√ 2 2 = 2.5√ 2

Читайте также: