Случайные величины и их числовые характеристики кратко

Обновлено: 05.07.2024

Понятие случайной величины является одним из центральных понятий теории вероятностей. Под случайной величиной понимается величина, принимающая в результате испытания то или иное (но при этом только одно) возможное значение, заранее не известное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. Случайная величина характеризует все возможные результаты случайного эксперимента с количественной стороны, однако, нельзя достоверно предсказать, какое именно значение при этом она примет.

Случайные величины обозначают обычно большими латинскими буквами, например X, Y, Z, или малыми греческими буквами, например x, z, h, а их возможные значения – малыми латинскими буквами, например x, y, z.

Случайные величины могут быть дискретными и непрерывными. Дискретной случайной величиной (ДСВ) называют такую величину, которая принимает отдельные, изолированные значения с определенными вероятностями. Непрерывной случайной величиной (НСВ) называют такую величину, которая может принимать любое значение из некоторого конечного или бесконечного числового промежутка.

Например, можно считать, что число покупателей в магазине, побывавших там в течение дня, число автомобилей, ремонтируемых еженедельно в данной мастерской, число пассажиров, находящихся в аэропорту, являются ДСВ. Курс валют, доход, объем ВНП и т.п. обычно рассматриваются как НСВ.

Для описания случайной величины используется функция распределения – функция F(x), которая определяет вероятность того, что случайная величина X примет значение меньше, чем x, т.е.

На рис. 2.1 изображены характерные графики функций распределения ДСВ (рис. 2.1а) и НСВ (рис. 2б).

Из определения функции распределения вытекают следующие ее свойства:

1 0 . Функция распределения F(x) есть неотрицательная функция, заключенная между нулем и единицей: .

2 0 . Функция распределения F(x) есть неубывающая функция, т.е. .

3 0 . Функция распределения F(x) изменяется от 0 до 1 при изменении x от–¥ до +¥:

Для описания ДСВ на практике обычно используется закон распределения (или ряд распределения) вероятностей случайной величины – это когда каждому возможному значению случайной величины ставится в соответствие некоторая вероятность.

Закон распределения обычно записывают в виде таблицы:

X	x₁	x₂	…	x_k
P	p₁	p₂	…	p_k

Пример 2.8. Доход от некоторого рискованного бизнеса составляет сумму около 1000 у.е. с заданным законом распределения (знак минус означает убыток):

Какой наиболее вероятностный денежный доход рискованного бизнеса? Является ли этот риск вероятностно-успешным?

Решение. Поскольку сумма всех вероятностей

Можно отметить, что для НСВ справедливы равенства

Пример 2.9. Пусть плотность распределения случайной величины X имеет вид

Найти значение постоянной C. Чему равна вероятность того, что данная случайная величина примет значение, лежащее на интервале (0;1)?

Решение. Чтобы функция f(x) была плотностью распределения, должны выполняться два условия: 1 0 и 2 0 . Из первого условия имеем C³0. По второму условию интеграл

должен быть равен 1. Отсюда C=1.

Искомая вероятность может быть найдена при помощи свойства 3 0 . В нашем случае

Функция распределения содержит достаточно полную информацию о случайной величине. Действительно, функция распределения одновременно указывает на то, какие значения может принимать случайная величина и с какими вероятностями. Однако судить об основных особенностях случайной величины только по виду функции распределения довольно трудно. Еще труднее сравнивать случайные величины. В связи с этим вводят более простые характеристики случайной величины, определяемые только одним числом. Хотя числовые характеристики не дают полного представления о случайной величине, однако они в сжатой форме выражают наиболее важные черты распределения.

Условно числовые характеристики разделяют на два класса: характеристики положения (математическое ожидание, мода, медиана, начальные моменты) и характеристики рассеивания (дисперсия, среднее квадратичное отклонение, центральные моменты). Важнейшими из них являются математическое ожидание, дисперсия, среднее квадратичное отклонение.

Математическое ожидание характеризует среднее ожидаемое значение случайной величины, т.е. приближенно равно ее среднему значению. Для решения многих задач достаточно знать эту величину. Например, при оценивании покупательской способности населения вполне может хватить знания среднего дохода. При анализе выгодности двух видов деятельности можно ограничиться сравнением их средних прибыльностей.

Математическое ожидание ДСВ определяется следующим образом

Математическое ожидание НСВ находится по формуле

Из определения математического ожидания вытекают следующие ее свойства:

1 0 . , где С – постоянная величина.

2 0 . .

3 0 . .

4 0 . , если X и Y – независимые случайные величины.

Для дальнейшего анализа случайных величин знания одного лишь математического ожидания недостаточно. Существуют отличные друг от друга случайные величины, имеющие одинаковые математические ожидания. Например, средний уровень жизни в Швеции и США приблизительно одинаков, однако разброс в доходах в этих странах существенно отличается. Акции двух компаний могут приносить в среднем одинаковые дивиденды, однако вложение денег в одну из них может быть гораздо более рискованной операцией, чем в другую. Следовательно, нужна числовая характеристика, которая оценивает разброс возможных значений случайной величины относительно ее математического ожидания. Такой наиболее распространенной характеристикой является дисперсия.

Дисперсией называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

где . Раскрыв скобки и используя свойства математического ожидания, получим формулу, которая довольно часто используется для вычисления дисперсии:

Из определения дисперсии вытекают следующие ее свойства:

1 0 . , где С – постоянная величина.

2 0 . .

3 0 . , если X и Y – независимые случайные величины.

Дисперсия имеет размерность, равную квадрату размерности случайной величины, что не всегда удобно при исследовании случайной величины. Для того чтобы представить разброс значений случайной величины в тех же единицах, что и сама случайная величина, вводится числовая характеристика – среднее квадратичное отклонение.

Средним квадратичным отклонением (СКО) называется квадратный корень из дисперсии:

Чтобы оценить разброс значений случайной величины в процентах относительно ее среднего значения, вводится коэффициент вариации, рассчитываемый по формуле:

Пример 2.10. По данным примера 2.8 определить, чему равен на длительный период средний доход от рассмотренного бизнеса? Какова мера риска вложений в такое предприятие?

Решение. Средний доход от рассмотренного бизнеса за длительный период равен математическому ожиданию:

Мерой риска вложений в рискованное предприятие может служить среднее квадратичное отклонение. Вычислим дисперсию по формуле (2.15), предварительно найдем

Следовательно, СКО будет равна

Коэффициент вариации в данном случае равен

Таким образом, разброс значений случайной величины достаточно большой, следовательно, рассматриваемый бизнес имеет очень высокий уровень риска. â

Пример 2.11. По данным примера 2.9 вычислить математическое ожидание и дисперсию?

Решение. По определению

Однако этот интеграл равен нулю, т.к. подынтегральная функция является нечетной. Таким образом

При решении многих практических задач не всегда нужно характеризовать случайную величину полностью, т. е. определять законы распределения. Кроме того, построение функции или ряда распределений для дискретной, а плотности - для непрерывной случайной величины громоздко и излишне.

Иногда достаточно указать отдельные числовые параметры, частично характеризующие особенности распределения. Необходимо знать некоторое среднее значение каждой случайной величины, около которого группируется ее возможное значение, или степень разбросанности этих значений относительно среднего и т. п.

Характеристики наиболее существенных особенностей распределения называются числовыми характеристиками случайной величины. С их помощью облегчается решение многих вероятностных задач без определения для них законов распределения.

Важнейшей характеристикой положения случайной величины на числовой оси является математическое ожидание М[X] = а, которое иногда называется средним значением случайной величины. Для дискретной случайной величины X с возможными значениями x₁, x₂, …, x_n и вероятностями p₁, p₂,…, p_n его определяют по формуле

Учитывая, что =1, можно записать

Таким образом, математическим ожиданием дискретной случайной величины называется сумма произведений возможных ее значений на их вероятности. Среднее арифметическое значение наблюдаемых значений случайной величины при большом числе опытов приближается к ее математическому ожиданию.

Для непрерывной случайной величины X математической ожидание определяется не суммой, а интегралом

где f(x) — плотность распределения величины X.

Математическое ожидание существует не для всех случайных величин. Для некоторых из них сумма, или интеграл, расходится, и, следовательно, математического ожидания не существует. В этих случаях по соображениям точности следует ограничивать область возможных изменений случайной величины X, для которых сумма, или интеграл, будут сходиться.

На практике применяются и такие характеристики положения случайной величины, как мода и медиана.

Модой случайной величины называется ее наиболее вероятное значение. В общем случае мода и математическое ожидание не совпадают.

Медианой случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т. е. это абсцисса точки, в которой ограниченная кривой распределения площадь делится пополам. Для симметричного распределения все три характеристики совпадают.

Кроме математического ожидания, моды и медианы в теории вероятностей используются и другие характеристики, каждая из которых описывает определенное свойство распределения. Например, числовыми характеристиками, характеризующими рассеивание случайной величины, т. е. показывающими, насколько тесно сгруппированы ее возможные значения около математического ожидания, являются дисперсия и среднее квадратическое отклонение. Они существенно дополняют случайную величину, так как в практике часто встречаются случайные величины с равными математическими ожиданиями, но различными распределениями. При определении характеристик рассеивания используют разность между случайной величиной X и ее математическим ожиданием, т. е.

где а = М[X] — математическое ожидание.

Эта разность называется центрированной случайной величиной, соответствующей величине X, и обозначается :

Дисперсия случайной величины - это математическое ожидание квадрата отклонения величины от ее математического ожидания, т. е.:

D[X]=M[(X – a) 2 ], или

Дисперсия случайной величины является удобной характеристикой рассеивания и разбросанности значений случайной величины около ее математического ожидания. Однако она лишена наглядности, так как имеет размерность квадрата случайной величины.

Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Такой величиной является среднее квадратическое отклонениеслучайной величины, которое представляет собой положительный квадратный корень из ее дисперсии.

Математическое ожидание, мода, медиана, дисперсия, среднее квадратическое отклонение - наиболее часто используемые числовые характеристики случайных величин. При решении практических задач, когда невозможно определить закон распределения, приблизительным описанием случайной величины являются ее числовые характеристики, выражающие какое-либо свойство распределения.

Кроме основных характеристик распределения центра (математического ожидания) и рассеивания (дисперсии) часто нужно описать другие важные характеристики распределения - симметрию и островершинность, которые можно представить с помощью моментов распределения.

Распределение случайной величины, полностью задано, если известны все его моменты. Однако многие распределения можно полностью описать с помощью первых четырех моментов, которые являются не только параметрами, описывающими распределения, но имеют также важное значение при подборе эмпирических распределений, т. е. вычислив числовые значения моментов для заданного статистического ряда и, использовав специальные графики, можно определить закон распределения.

В теории вероятностей различают моменты двух видов: начальные и центральные.

Начальным моментом k-го порядка случайной величины Т называют математическое ожидание величины X k , т. е.

Следовательно, для дискретной случайной величины он выражается суммой

а для непрерывной – интегралом

Среди начальных моментов случайной величины особое значение имеет момент первого порядка, который является математическим ожиданием. Начальные моменты высших порядков используются, главным образом, для вычисления центральных моментов.

Центральным моментом k-го порядка случайной величины называют математическое ожидание величины (X - М [X]) k

где а = М [X].

Для дискретной случайной величины он выражается суммой

а для непрерывной – интегралом

Среди центральных моментов случайной величины особое значение имеет центральный момент второго порядка, который представляет дисперсию случайной величины.

Центральный момент первого порядка всегда равен нулю.

Третий начальный момент характеризует асимметрию (скошенность) распределения и по результатам наблюдений для дискретной и непрерывной случайных величин определяется соответствующими выражениями:

Поскольку он имеет размерность куба случайной величины, то, чтобы получить безразмерную характеристику, m₃ делят на среднее квадратическое отклонение в третьей степени

Полученная величина называется коэффициентом асимметрии и в зависимости от знака характеризует положительную (As > 0) или отрицательную (As 2 ], или

В теории вероятностей различают моменты двух видов: начальные и центральные.

Начальным моментом k-го порядка случайной величины Т называют математическое ожидание величины X k , т. е.

Следовательно, для дискретной случайной величины он выражается суммой

а для непрерывной – интегралом

Центральным моментом k-го порядка случайной величины называют математическое ожидание величины (X - М [X]) k

где а = М [X].

Для дискретной случайной величины он выражается суммой

а для непрерывной – интегралом

Центральный момент первого порядка всегда равен нулю.

Полученная величина называется коэффициентом асимметрии и в зависимости от знака характеризует положительную (As > 0) или отрицательную (As

Перечислим основные характеристики случайных величин:
— математическое ожидание (характеризует среднее значение);
— дисперсия;
— среднеквадратическое отклонение;
— медиана случайной величины;
— мода случайной величины;
— начальный момент;
— центральный момент;
— аcсимметрия;
— эксцесс;
— квантиль уровня.

Медиана случайной величины — это такое значение случайной величины X, при котором X=Me и Me разделяет область значений на две части, вероятности попадания в любую из данных областей равновероятны, то есть выполняется условие:

p(X Me)

F(Me)=0.5

Модой для дискретной случайной величины называют такое значение, которое наиболее вероятно.

Модой для непрерывной случайной величины называют наибольшее значение (точка локального максимума) плотности вероятности.

Мода и медиана на графике

Начальным моментом порядка k случайной величины X называется математическое ожидание величины Х k и определяется равенством:

Формула начального момента для непрерывной случайной величины:

Формула начального момента для дискретной случайной величины:

Центральным моментом порядка k случайной величины X называется математическое ожидание величины (X-M(Х)) k и определяется равенством:

Формула центрального момента для непрерывной случайной величины:

Формула центрального момента для дискретной случайной величины:

Центральный момент первого порядка случайной величины X равен нулю, то есть

Центральный момент второго порядка случайной величины X равен дисперсии, то есть

Центральный момент третьего порядка случайной величины X характеризует асимметрию и определяется равенством:

Центральный момент четвёртого порядка случайной величины X характеризует эксцесс и равен:

Асимметрия характеризует меру сдвига распределения случайной величины в левую или правую часть и находится по формуле:

Эксцесс — характеристика вогнутости и выпуклости распределения случайной величины и вычисляется по формуле:

График значений коэффициента эксцесса

Квантилем уровня p называют такое значение случайной величины x_p которое удовлетворяет условие:

4874

Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:

Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.

Случайные величины, как правило, обозначают через *, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .

* Иногда используют , а также греческие буквы

Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:

– количество очков, которое выпадет после броска игрального кубика.

В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина может принять одно из следующий значений:

– количество мальчиков среди 10 новорождённых.

Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:

, либо мальчиков – один и только один из перечисленных вариантов.

И, дабы соблюсти форму, немного физкультуры:

– дальность прыжка в длину (в некоторых единицах).

Её не в состоянии предугадать даже мастер спорта :)

Тем не менее, ваши гипотезы?

Коль скоро речь идёт о множестве действительных чисел, то случайная величина может принять несчётно много значений из некоторого числового промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.

Таким образом, случайные величины целесообразно разделить на 2 большие группы:

1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.

…нарисовались непонятные термины? Срочно повторяем основы алгебры!

2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.

Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ

Сначала разберём дискретную случайную величину, затем – непрерывную.

Закон распределения дискретной случайной величины

А теперь очень важный момент: поскольку случайная величина обязательно примет одно из значений , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:

или, если записать свёрнуто:

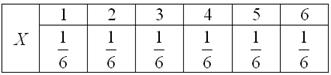
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:

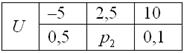
Некоторая игра имеет следующий закон распределения выигрыша:

…наверное, вы давно мечтали о таких задачах :) Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.

Решение: так как случайная величина может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:

– таким образом, вероятность выигрыша условных единиц составляет 0,4.

Контроль: , в чём и требовалось убедиться.

Ответ:

Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:

В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины – размера выигрыша, если из коробки наугад извлекается один билет.

Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно рублей.

Всего таковых билетов 50 – 12 = 38, и по классическому определению:
– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.

С остальными случаями всё просто. Вероятность выигрыша рублей составляет:

Проверка: – и это особенно приятный момент таких заданий!

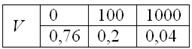
Ответ: искомый закон распределения выигрыша:

Следующее задание для самостоятельного решения:

Вероятность того, что стрелок поразит мишень, равна . Составить закон распределения случайной величины – количества попаданий после 2 выстрелов.

…я знал, что вы по нему соскучились :) Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.

Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.

Математическое ожидание дискретной случайной величины

Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:

или в свёрнутом виде:

Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:

В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.

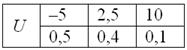
Теперь вспомним нашу гипотетическую игру:

, таким образом, математическое ожидание данной игры проигрышно.

Не верь впечатлениям – верь цифрам!

Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры :) Ну, может, только ради развлечения.

Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.

Творческое задание для самостоятельного исследования:

Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.

Но прежде будет полезно размять пальцы на клавишах калькулятора:

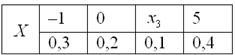
Случайная величина задана своим законом распределения вероятностей:

Найти , если известно, что . Выполнить проверку.

Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.

Решения и ответы:

Пример 3. Решение: по условию – вероятность попадания в мишень. Тогда:
– вероятность промаха.

Составим – закон распределения попаданий при двух выстрелах:

– два попадания. По теореме умножения вероятностей независимых событий:

Проверка: 0,09 + 0,42 + 0,49 = 1

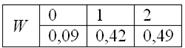
Ответ:

Примечание: можно было использовать обозначения – это не принципиально.

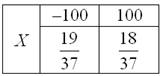
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид:

Вычислим математическое ожидание:

Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.

Пример 5. Решение: по определению математического ожидания:

поменяем части местами и проведём упрощения:

таким образом:

Выполним проверку:

, что и требовалось проверить.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Аннотация: Даются основные определения, рассматриваются гистограмма, полигон частот, непрерывное распределение и свойства основных характеристик случайной величины.

Основные определения и понятия

Расширением понятия случайных событий, состоящих в появлении некоторых числовых значений в результате эксперимента, является случайная величина Х.

Определение. Случайной называют величину, принимающую в результате эксперимента одно только значение из некоторой их совокупности и неизвестное заранее, какое именно.

Случайная величина , к примеру, представляет собой обоснованную модель описания геологических данных, учитывающую влияние различных факторов на физическое поле .

Как и результат отдельного эксперимента, точное значение случайной величины предсказать нельзя, можно лишь установить ее статистические закономерности, т.е. определить вероятности значений случайной величины. Например, измерения физических свойств горных пород являются наблюдениями соответствующих случайных величин.

Среди случайных величин, с которыми приходится встречаться геологу, можно выделить два основных типа: величины дискретные и величины непрерывные.

Определение. Дискретной случайной величиной называется такая, которая может принимать конечное или бесконечное счетное множество значений.

В качестве типичных примеров дискретной случайной величины могут выступать все результаты полевых работ , все результаты экспериментов, привезенные c поля образцы и пр.

Всевозможные значений случайной величины образуют полную группу событий, т.е. ^n p_=1$" />
, где - конечное или бесконечное. Поэтому можно говорить, что случайная величина обобщает понятие случайного события.

Пусть в результате исследований был получен следующий ряд данных по количественному составу некоторой породы: 4; 3; 1; 2; 5; 4; 2; 2; 3; 1; 5; 4; 3; 5; 5; 2; 5; 5; 6; 1. Всего было проведено 20 испытаний. Для того, чтобы с данными было удобно работать, их преобразовали: расположили полученные значения по возрастанию и подсчитали количество появления каждого из значений. В результате получили (Таблица 7.1):

Определение. Распределение данных по возрастанию называется ранжированием.

Определение. Наблюдаемое значение некоторого признака случайной величины называется вариантом.

Определение. Ряд, составленный из вариант, называется вариационным рядом.

Определение. Изменение некоторого признака случайной величины называется варьированным.

Определение. Вероятность появления данной варианты равно отношению частоты к общей сумме вариационного ряда

$P_<x_<i>>=\frac >$

( 1)

С учетом введенных определений перепишем таблицу 7.1.

При статистическом анализе экспериментальных данных главным образом используется дискретные величины. В таблице 7.3 приведены основные числовые характеристики этих величин, имеющих важное практическое значение при обработке экспериментальных данных.

$M_<X>=\sum\limits_^n p_x_$

( 2)

$\overline X=\frac 1 N \sum\limits_<i=1>^n x_$

( 3)

$D_=M \left ( X-M_\right )^2=\sum\limits_^n p_ \left ( x_-\overline x \right ) ^2$

( 4)

$\sigma=\sqrt <D_<X>>$

( 5)

$V=\frac <\sigma>X$

( 6)

$\overline <x_<i>>=\frac <\left ( x_<i>-\overline x \right )>$

( 7)

$m_<k>=M_^k=\sum\limits_^n p_x_^k$

( 8)

$\mu_<k>=M \left ( X-M_\right )^k=\sum\limits_^n p_ \left ( x_-\overline x \right ) ^k$

( 9)

$A=\frac <\mu_<3>>$

( 10)

$E=\frac <\mu_<4>> -3$

( 11)

В таблице п. 8 – 12 используются для статистической обработки вариационных рядов. Об их использовании будет материал немного дальше.

В заключении заметим, что, если результат эксперимента описывается двумя и более случайными величинами, то говорят о системе случайных величин. К системе случайных величин, например, могут быть отнесены физические свойства образцов горных пород, характеристики аномальнообразующих тел, наблюдений различных полей, характеристики месторождений и т.д.

Читайте также: