Правила построения геометрии кратко

Обновлено: 03.07.2024

Загрузить презентацию (961 кБ)

Тема урока: Деление отрезка, угла, дуги на равные части (1час)

Формирование знаний, графических умений и навыков у школьников;
Развитие интеллектуальных данных в процессе изучения темы и освоения приемов построения чертежа;
Развитие познавательного интереса школьников, их мышления, пространственных представлений, творческих способностей;
Воспитание аккуратности и точности выполнения действий при выполнении графических работ

Методы:

Оборудование:

Тип урока:

Структура урока

Орг. момент – 1-2 мин.
Повторение – 5 мин.
Новый материал – 25 мин.
Практическая работа – 10 мин.
Заключительная часть урока – 4 – 3 мин.

Ход урока

Орг. момент.

Знакомство уч-ся с темой и планом проведения урока.

Проверить техническое оснащение учащихся (наличие чертежных инструментов)

Повторение

Повторение провести в форме фронтального опроса по материалу, изученного на уроках геометрии:

Что называется лучом? Углом? Прямой?
Какие углы по величине существуют?
Как они отличаются друг от друга? Дать краткую характеристику каждому.
Что такое отрезок?
Что такое перпендикуляр?
Как проводится перпендикуляр на определенной линии?

Новый материал

Для выполнения графических работ вместе с учителем необходимо иметь все чертежные инструменты и приспособления. Теоретический материал можно выполнять следующими способами:

Геометрическое построение - графический способ решения геометрических задач на плоскости при помощи чертежных инструментов

Оно включает
в себя:

Деление отрезка на равные части;
Деление угла и дуги на равные части;
Деление окружностей на равные части;
Создание орнамента с использованием техники деление окружностей на n-равных частей

1. Построение параллельных прямых с помощью линейки и угольника

2. Построение перпендикулярных прямых с помощью угольника и линейки (показать трудовые приемы)

3. Деление отрезка на равные части

4. Построение углов при помощи угольников

(Приложение 1 или обложка учебника)

5. Деление угла при помощи транспортира

6. Деление прямого угла на равные части

7. Нахождение центра дуги и определение величины радиуса

Практическая работа

В рабочей тетради вместе с учителем используя чертежные инструменты и приспособления выполнить следующую графическую работу:

Разделить на две части острый угол.
разделить на три части тупой угол.

Заключительная часть Подведение итога.

Указать на типичные ошибки и найти способы их устранения.
Оценить работу учащихся на уроке.

Домашнее задание

Читать §15 п.1.
Выполнить графическую работу по индивидуальным карточкам (согласно своего варианта).

Тема урока: Деление окружностей на равные части. Орнамент

Формирование знаний, графических умений и навыков у школьников;
Развитие интеллектуальных данных в процессе изучения темы и освоения приемов построения чертежа, с применением правил деления окружностей на равные части;
Развитие познавательного интереса школьников, их мышления, пространственных представлений, творческих способностей;
Воспитание аккуратности и точности выполнения действий при выполнении графических работ

Методы:

Оборудование:

Структура урока

Орг. момент – 1-2 мин.
Повторение - 5 мин.
Новый материал – 25 мин.
Практическая работа – 10 мин.
Заключительная часть урока – 4 – 3 мин.

Ход урока

Орг. момент.

Знакомство уч – ся с темой и планом проведения урока.

Проверить техническое оснащение учащихся (наличие чертежных инструментов).

Повторение

Повторение провести в форме тестирования по изученному материалу на прошлом уроке.

Новый материал

Оно включает
в себя:

Деление отрезка на равные части;
Деление угла и дуги на равные части;
Деление окружностей на равные части;
Создание орнамента с использованием техники деление окружностей на n-равных частей

1. Деление окружностей на 4 и 8 равных частей

2. Деление окружностей при помощи угольников

(слайды 10, 12, 13, 15)

3. Деление окружностей
на 3 и 6 равных частей

4. Деление окружностей на 5 и 10 равных частей

5. Создание орнамента

Практическая работа

В рабочей тетради с помощью учителя. используя чертежные инструменты и приспособления выполнить следующую графическую работу:

Понять геометрию с нуля — это непросто. Но, чем дальше, тем интереснее. Новые знания можно применить везде: в школе на уроках, дома во время ремонта и даже на прогулке. В этой статье рассказали про основы геометрии для начинающих.

О чем эта статья:

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Математика занимается объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

Обозначать прямые принято малыми латинскими буквами (a, b, c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

Два варианта расположения точек относительно прямой:

Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).

Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).

Если рассмотреть две прямые, то возможны два варианта их расположения:

Прямые пересекаются, то есть имеют одну общую точку.

Для записи пересекающихся прямых используют специальный знак — ∩, то есть a∩b (читают: прямая a пересекает прямую b). Чтобы обозначить точку пересечения прямых, пишут a∩b = O (читается: прямая a пересекается с прямой b в точке O).

Для записи не пересекающихся прямых используют специальный знак — , то есть m n (читают: прямая m не пересекает прямую n). В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.

Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Комбинации простейших объектов

Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).

Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.

Точно так же мы изучали множества, а после — отношения между множествами, функции.

Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.

Максимальный угол – это полный оборот, он составляет 360 градусов.

Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.

Есть разные виды углов, выделим самые часто встречающиеся:

Если градусная мера угла меньше 90° — угол острый.

Если градусная мера угла равна 90° — угол прямой.

Если градусная мера угла больше 90°, но меньше 180° — угол тупой.

Если градусная мера угла равна 180° — угол развернутый.

Общая точка, из которой исходят лучи, называется вершиной угла, а лучи — сторонами угла.

Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.

Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.

Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.

А теперь посмотрим на взаимное расположение трех прямых.

Первый случай: все три прямые параллельны.

Второй случай: две прямые параллельны, а третья их пересекает.

Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.

Треугольник

Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.

Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.

Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.

Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:

две стороны и угол между ними;

два угла и сторону;

Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Неравенство треугольника

Сумма любых двух сторон треугольника больше его третьей стороны.

Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.

Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.

Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.

Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.

От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃

Четырехугольники

Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.

Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.

Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:

Окружность

Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.

Практическая сторона геометрии

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Построение отрезка, равного данному

Есть отрезок СD. Задача - начертить равнозначный данному отрезок той же величины.

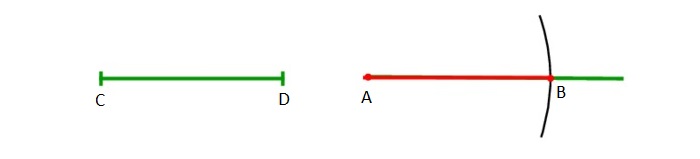
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

Деление отрезка пополам

Имеется отрезок AB.

Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Построение угла, равного данному

Имеется угол ABC.

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Построение перпендикулярных прямых

Пример 1

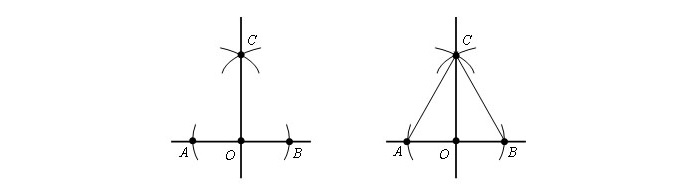
Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка - AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O₁ - место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО₁ и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO₁A. Из данного вывода следует, что угол OAC = O₁AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O₁CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

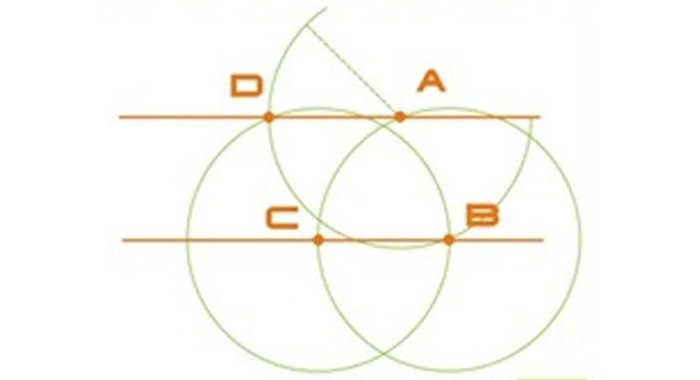
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Построение правильного четырехугольника вписанного в окружность

Вариант 1

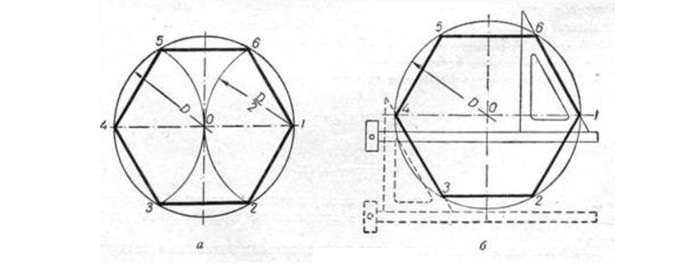
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

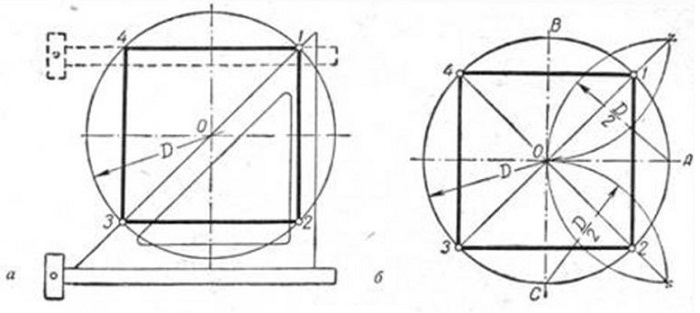
Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

Из многочисленных построений здесь рассматриваются только те, которые часто встречаются при выполнении чертежей.

Деление отрезка прямой на две и четыре равные части выполняется в следующей последовательности.

Из концов отрезка А В циркулем проводят две дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения в точках n и m (рис. 43, а). Точки тип соединяют прямой, которая пересекает отрезок АВ в точке С. Точка С делит отрезок А В на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка СВ, разделим отрезок на четыре равные части.

При вычерчивании детали, показанной на рис. 43, б, применяется способ деления отрезка на четыре части.

Деление отрезка прямой на любое число равных частей. Пусть отрезок А В требуется разделить на И равных частей. Для этого из любого конца данного отрезка, например из точки В (рис. 44, проводят под произвольным острым углом вспомогательную прямую линию ВС, на которой от точки В измерительным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой А прямой Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой которые и разделяют отрезок А В на 11 равных частей.

На рис. 44, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части.

ПОСТРОЕНИЕ И ИЗМЕРЕНИЕ УГЛОВ ТРАНСПОРТИРОМ

Транспортир — это прибор для измерения и построения углов. Это полукруг с разбивкой на градусы, соединенный с опорной планкой.

Для измерения угла транспортир прикладывают опорной планкой к одной из сторон данного угла (рис. 45, а) так, чтобы вершина угла (точка А) совпадала с точкой О на транспортире. Величину угла САВ в градусах определяют по шкале транспортира.

Для построения угла заданной величины (в градусах) со стороной А В и вершиной в точке к прикладывают транспортир так, чтобы его центр (точка О) совпал с точкой А прямой АВ, затем у деления шкалы транспортира, соответствующего заданному числу градусов (например, 55°), наносят точку n. Транспортир убирают и проводят через точку n отрезок АС — получают заданный угол САВ (рис. 45, б).

Углы можно строить при помощи угольников с углами 45, 30 и 60° и линейки или рейсшины. На рис. 46 показано, как при различных положениях угольников на рейсшине можно строить углы 60 (120), 30 (150), 45° (135°) и другие при использовании одновременно двух угольников..

ПОСТРОЕНИЕ И ДЕЛЕНИЕ УГЛОВ

Деление угла на две и четыре равные части. Из вершины угла провести произвольным радиусом дугу до пересечения со сторонами угла в точках (рис. 47, а). Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги n и к, до взаимного пересечения в точке m. Вершину угла соединяют с точкой т прямой, которая делит угол ВАС пополам. Эта прямая называется биссектрисой угла ВАС. Повторяя это построение с полученными углами В Ат и nАС угол ВАС можно разделить на четыре равные части и т. д.

Деление прямого угла на три равные части. Из вершины А прямого угла (рис. 47, б) произвольным радиусом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла А прямыми и получают стороны Аm и Аn углов В Аm и nА С,равных 1/3 прямого угла, т. е. 30°. Если каждый из этих углов разделить пополам, то прямой угол будет разделен на шесть равных частей, каждый из углов будет равняться 15°. Прямой угол АВС можно разделить на три равные части угольником с углами 30 и 60° (рис. 48, а). При выполнении чертежей нередко требуется разделить прямой угол на две равные части. Это можно выполнять угольником с углом 45° (рис. 48, б).

Построение угла, равного данному. Пусть задан угол ВАС. Требуется построить такой же угол. Через произвольную точку А₁ проводим прямую А₁С₁. Из точки А описываем дугу произвольным радиусом R, которая пересечет угол ВАС в точках (рис. 49,а). Из точки A ₁ проводим дугу тем же радиусом и получаем точку m₁. Из точки A₁ проводим дугу радиусом R₁ равным отрезку mn, до пересечения с ранее проведенной дугой радиуса R в точке n₁ (рис. 49, б). Точку n₁ соединяем с точкой А₁ и получаем угол B₁A₁C₁ величина которого равна заданному углу ВАС.

Применение вышеизложенного построения угла по заданному показано на рис. 49, в и г. На рис. 49, в изображена деталь, чертеж которой надо вычертить, а на рис. 49, г показан этот чертеж, при выполнении которого использован способ построения угла по заданному.

СПОСОБЫ ПОСТРОЕНИЯ МНОГОУГОЛЬНИКОВ

Способ триангуляции. Построение многоугольников этим способом основано на последовательном построении ряда треугольников, примыкающих сторонами друг к другу. Этот способ будет применяться в дальнейшем при построении разверток поверхностей геометрических тел.

Рассмотрим пример такого построения. На рис. 50, а показана пластина с пятиугольным отверстием. Измеряя длины сторон пятиугольника, можно построить на чертеже контурное очертание многоугольного отверстия.

Треугольники в рассматриваемом многоугольнике можно получить, проведя диагонали 14 (рис. 50, а). Последовательность построения многоугольника на чертеже в данном примере следующая.

На детали произвольно выбираем базовую линию (например, А В), на которую из точек 7 и 2 опускаем перпендикуляр, и получаем точки E и G. На чертеже наносим базовую линию A₁B₁ на которой откладываем отрезок E₁G₁ равный отрезку EG. Из точек и G, восставляем перпендикуляры, на которых откладываем взятые с детали отрезки и G1 (рис. 50, б). Получим точки 1₁и2₁. Из точек как из центров, циркулем описываем две дуги радиусами, равными отрезками 13 и 23, взятых с детали. Точка пересечения дуг является вершиной 3₁ искомого треугольника 1₁2₁3₁. Таким же способом из точек 7₁ и 3₁ описываем две дуги радиусами, равными отрезкам 34 и 14, находим вершину 4₁. Затем из точек 4₁ и 1₁, как из центров, описываем две дуги радиусами, равными отрезкам 45 и 15, определяем последнюю вершину пятиугольника 5₁(рис. 50, б).

ОПРЕДЕЛЕНИЕ ЦЕНТРА ДУГИ ОКРУЖНОСТИ

Многие детали машин и приборов имеют контур очертания, состоящий из прямых линий, лекальных кривых и дуг окружностей. При вычерчивании деталей часто приходится определять величину радиусов дуг окружностей контурных очертаний детали и находить положение центров этих дуг. На рис. 51, а показана деталь (кронштейн), левая часть ребра которой выполнена по дуге окружности.

Чтобы найти положение центра и величину радиуса данной дуги, предварительно делают отпечаток дуги на бумаге. При помощи циркуля и линейки можно определить центр и размер радиуса дуги окружности, для этого на отпечатке дуги намечают три произвольно расположенные на ней точки А, В и С (рис. 51, б) и проводят хорды АВ и ВС. При помощи циркуля и линейки проводят перпендикуляры через середины хорд А В и ВС. Точка пересечения перпендикуляров

(точка О) является искомым центром дуги детали, а расстояние от точки О до любой точки дуги будет размером радиуса.

Читайте также: