Основные понятия тригонометрии кратко
Обновлено: 04.07.2024
У многих учеников возникают проблемы с этой темой, в основном, из-за непонимания общего смысла тригонометрии. В этой статье я постараюсь помочь вам разобраться зачем нужна тригонометрия и расскажу про лайфхак, чтобы не учить значения синуса и косинуса.
К моменту начала изучения тригонометрии Вы, скорее всего, уже знаете: определение прямоугольного треугольника и окружности — этого вполне достаточно для понимания темы.
*прошу заметить, что некоторые формулировки могут не соответствовать действительности - это сделано для того, чтобы вы лучше запомнили основы. Точные понятия и определения расскажет ваш учитель математики.
Что такое синус и косинус?
Изначально не было никакой окружности. Изучая треугольники, древние ученые выражали углы через соотношение сторон. То-есть синусы и косинусы появились раньше градусной меры углов.
Поскольку угол может быть найден через разные соотношения сторон, решили дать им названия: синус и косинус.
Синус - это отношение стороны треугольника, лежащей напротив данного угла, к гипотенузе (большей стороне).
Косинус - это отношение прилежащей стороны к гипотенузе.
Думаю не ошибусь, если скажу, что теорема Пифагора - самая полезная теорема в геометрии. Давайте применим её для данного треугольника:
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии "на пальцах".
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA') равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC'D', построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Например, значения тригонометрических функций для углов 270° и -90° равны.
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π .
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
ТРИГОНОМЕТРИЯ – (от греч. trigwnon – треугольник и metrew – измеряю) – математическая дисциплина, изучающая зависимости между углами и сторонами треугольников и тригонометрические функции.
В тригонометрии выделяют три вида соотношений: 1) между самими тригонометрическими функциями; 2) между элементами плоского треугольника (тригонометрия на плоскости); 3) между элементами сферического треугольника, т.е. фигуры, высекаемой на сфере тремя плоскостями, проходящими через ее центр. Тригонометрия началась именно с наиболее сложной, сферической части. Она возникла прежде всего из практических нужд. Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников. По звездам вычисляли местонахождение корабля в море или направление движения каравана в пустыне. Наблюдения за звездным небом с незапамятных времен вели и астрологи.
Естественно, все измерения, связанные с расположением светил на небосводе, – измерения косвенные. Прямые могли быть проведены только на поверхности Земли, но и здесь далеко не всегда удавалось непосредственно определить расстояние между какими-то пунктами и тогда вновь прибегали к косвенным измерениям. Например, вычисляли высоту дерева, сравнивая длину его тени с длиной тени от какого-нибудь шеста, высота которого была известна. Аналогичным образом вычисляли и размеры острова в море. Подобные задачи сводятся к анализу треугольника, в котором одни его элементы выражают через другие. Этим и занимается тригонометрия. А поскольку звезды и планеты представлялись древним точками на небесной сфере, то сначала стала развиваться именно сферическая тригонометрия. Ее считали разделом астрономии.
А начиналось все очень давно. Первые отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. Астрономы Междуречья научились предсказывать положение Земли и Солнца и именно от них к нам пришла система измерения углов в градусах, минутах и секундах, потому что у вавилонян была принята шестидесятеричная система счисления.
Однако первые по-настоящему важные достижения принадлежат древнегреческим ученым. Например, 12-я и 13-я теоремы второй книги Начал Евклида (конец 4–3 в. до н. э.) выражают по существу теорему косинусов. Во 2 в. до н.э. астроном Гиппарх из Никеи (180–125 до н.э.) составил таблицу для определения соотношений между элементами треугольников. Такие таблицы нужны потому, что значения тригонометрических функций нельзя вычислить по аргументам с помощью арифметических операций. Тригонометрические функции приходилось рассчитывать заранее и хранить в виде таблиц. Гиппарх подсчитал в круге заданного радиуса длины хорд, отвечающих всем углам от 0 до 180°, кратным 7,5°. По существу, это таблица синусов. Труды Гиппарха до нас не дошли, но многие сведения из них включены в Альмагест (II в.) – знаменитое сочинение в 13 книгах греческого астронома и математика Клавдия Птолемея (ум. ок.160 н. э.). Древние греки не знали синусов, косинусов и тангенсов, вместо таблиц этих величин они употребляли таблицы, позволявшие находить хорду окружности по стягиваемой дуге. В Альмагесте автор приводит таблицу длин хорд окружности радиуса в 60 единиц, вычисленных с шагом 0,5° с точностью до 1/3600 единицы, и объясняет, как эта таблица составлялась. Труд Птолемея несколько веков служил введением в тригонометрию для астрономов.
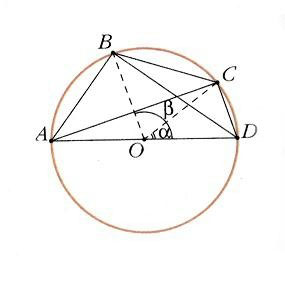
Чтобы понять, как ученые древности составляли тригонометрические таблицы, надо познакомиться с методом Птолемея. Метод основан на теореме – произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений его противоположных сторон.
Пусть ABCD – вписанный четырехугольник, АD – диаметр окружности, а точка O – ее центр (рис. 1). Если известно, как вычислять хорды, стягивающие углы DOC = a и DОВ = b, т. е. сторону СD и диагональ B, то, по теореме Пифагора, из прямоугольных треугольников АDВ и АDС можно найти АВ и АС, а потом, по теореме Птолемея, – BC = (АС·ВD – АВ·СD) /АD, т.е. хорду, стягивающую угол ВОС = b – a. Некоторые хорды, например стороны квадрата, правильных шестиугольника и восьмиугольника, отвечающие углам 90, 60 и 45°, легко определить. Известна также сторона правильного пятиугольника, которая стягивает дугу в 72°. Приведенное выше правило позволяет вычислять хорды для разностей этих углов, например для 12° = 72° – 60°. Кроме того, можно находить хорды половинных углов, однако этого недостаточно, чтобы рассчитать, чему равна хорда дуги в 1°, – хотя бы потому, что все названные углы кратны 3°. Для хорды 1° Птолемей нашел оценку, показав, что она больше 2/3 хорды (3/2)° и меньше 4/3 хорды (3/4)° – двух чисел, совпадающих с достаточной для его таблиц точностью.
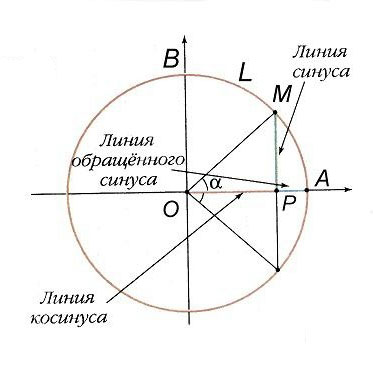
За единицу измерения отрезков MP, OP, PA принималась дуговая минута. Так, линия синуса дуги AB = 90° есть OB – радиус окружности; дуга AL, равная радиусу, содержит (округленно) 57°18' = 3438'.
Дошедшие до нас индийские таблицы синусов (древнейшая составлена в 4–5 веке н.э.) не столь точны, как птолемеевы; они составлены через 3°45' (т.е. через 1/24 часть дуги квадранта).
Большой вклад в развитие тригонометрии внесли арабские ученые, например, Аль-Баттани (ок. 900 н.э.). В 10 в. багдадский ученый Мухаммед из Буджана, известный под именем Абу-ль-Вефа (940–997), присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов. Он дает им те же определения, которые содержатся и в наших учебниках. Абу-ль-Вефа устанавливает и основные соотношения между этими линиями.
Итак, к концу 10 в. ученые исламского мира уже оперировали, наряду с синусом и косинусом, четырьмя другими функциями – тангенсом, котангенсом, секансом и косекансом; открыли и доказали несколько важных теорем плоской и сферической тригонометрии; использовали окружность единичного радиуса (что позволило толковать тригонометрические функции в современном смысле); придумали полярный треугольник сферического треугольника. Арабские математики составили точные таблицы, например таблицы синусов и тангенсов с шагом в 1' и точностью до 1/700 000 000. Очень важной прикладной задачей была и такая: научиться определять направление на Мекку для пяти ежедневных молитв, где бы ни находился мусульманин.
Особенно большое влияние на развитие тригонометрии оказал Трактат о полном четырехстороннике астронома Насир-эд-Дин из Туса (1201–1274), известного так же под именем ат-Туси. Это было первое в мире сочинение, в котором тригонометрия трактовалась как самостоятельная область математики.
В 12 в. был переведен с арабского языка на латинский ряд астрономических работ, по ним впервые европейцы познакомились с тригонометрией.
Трактат Насир-эд-Дина произвел большое впечатление на немецкого астронома и математика Иоганна Мюллера (1436–1476). Современники больше знали его под именем Региомонтана (так переводится на латинский название его родного города Кенигсберга, ныне – Калининграда). Региомонтан составил обширные таблицы синусов (через 1 минуту с точностью до седьмой значащей цифры). Он впервые отступил от шестидесятиричного деления радиуса и за единицу измерения линии синуса принял одну десятимиллионную часть радиуса. Таким образом, синусы выражались целыми числами, а не шестидесятиричными дробями. До введения десятичных дробей оставался только один шаг, но он потребовал более 100 лет. Труд Региомонтана О треугольниках всех родов пять книг сыграл в европейской математике ту же роль, что и сочинение Насир-эд-Дина в науке мусульманских стран.
За таблицами Региомонтана последовал ряд других, еще более подробных. Друг Коперника Ретик (1514–1576) вместе с несколькими помощниками в течение 30 лет работал над таблицами, законченными и изданными в1596 его учеником Отто. Углы шли через 10'', а радиус делился на 1 000 000 000 000 000 частей, так что синусы имели 15 верных цифр.
К концу 18 в. тригонометрия как наука уже сложилась. Тригонометрические функции нашли применение в математическом анализе, физике, химии, технике – везде, где приходится иметь дело с периодическими процессами и колебаниями – будь то акустика, оптика или качание маятника.
Решение любых треугольников, в конечном счете, сводится к решению прямоугольных треугольников (т.е. таких, у которых один из углов – прямой). Поскольку все прямоугольные треугольники с заданным острым углом подобны друг другу, отношения их соответственных сторон одинаковы. Например, в прямоугольном треугольнике ABC отношение двух его сторон, например, катета а к гипотенузе с, зависит от величины одного из острых углов, например А. Отношения различных пар сторон прямоугольного треугольника и называются тригонометрическими функциями его острого угла. Всего таких отношений в треугольнике шесть, и им отвечают шесть тригонометрических функций (обозначения сторон и углов треугольника на рис. 3).
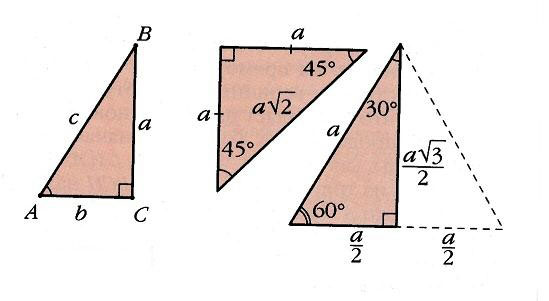
Синус (отношение противолежащего катета к гипотенузе),
косинус (отношение прилежащего катета к гипотенузе),
тангенс (отношение противолежащего катета к прилежащему),
котангенс (отношение прилежащего катета к противолежащему),
секанс sec A = (отношение гипотенузы к прилежащему катету),
косеканс cosec A = (отношение гипотенузы к противолежащему катету).
Из определений вытекает несколько равенств, связывающих тригонометрические функции одного и того же угла между собой:
С учетом теоремы Пифагора a 2 + b 2 = c 2 можно выразить все шесть функций через какую-нибудь одну. Например, синус и косинус связаны основным тригонометрическим тождеством
Некоторые соотношения между функциями:
Эти формулы справедливы и для тригонометрических функций любого угла, но ими надо пользоваться осторожно, поскольку правые и левые части могут иметь разные области определения.
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. Возьмем на координатной плоскости окружность радиуса с центром в начале координат. Пусть одна сторона угла α с вершиной в начале координат идёт по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс. Из геометрии известно, что отношение длины дуги , на которую опирается этот угол, к радиусу этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла:
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
и от радианного измерения к градусному:
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
| |||||||||||||
| Таблица 2.4.1.1
Определите радианную меру угла, если его градусная мера равна: 1) 2°; 2) 225°. Снова рассмотрим на координатной плоскости окружность радиуса с центром в начале координат. Как известно, координатные оси делят окружность на четыре дуги, которые называют четвертями . Рассмотрим произвольный угол α. Изобразим его как угол поворота радиус-вектора против часовой стрелки. При таком повороте точка перейдёт в некоторую точку на этой окружности, при этом (α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка , угол α называется углом этой четверти. Докажем, что отношения и не зависят от величины радиуса . Действительно, выберем на отрезке точку такую, что Построим окружность с центром в начале координат радиуса Построенная окружность пересекает радиус-вектор в точке Так как векторы и коллинеарны и одинаково направлены, то Однако равные векторы имеют равные координаты, следовательно, Откуда следует после деления обеих частей последних равенств на , что Итак, для любого угла поворота отношение координат радиус-вектора к его длине не зависит от этой длины радиус-вектора. Следовательно, отношения и характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например, . Так мы и сделаем. Окружность единичного радиуса с центром в начале координат называется тригонометрической окружностью . Ввиду всего вышесказанного, рассмотренные отношения и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить. Введём несколько ключевых определений. Косинусом угла α называется абсцисса точки − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс. Синусом угла α называется ордината точки − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс. Тангенсом угла α называется отношение ординаты к абсциссе точки − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс. Котангенсом угла α называется отношение абсциссы к ординате точки − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс. Ясно, что для данного угла α функции , которые называются тригонометрическими функциями , определены однозначно (поскольку каждому углу соответствует единственная точка на тригонометрической окружности). Однако если функции определены для любого угла α, то функции определены только для тех углов, для которых не равен нулю знаменатель дробей и Значит, не определён для углов вида где не определён для углов вида Поскольку синус по определению равен ординате точки на единичной окружности, а косинус − абсциссе, то знаки тригонометрических функций по четвертям будут такими: Найдём значения тригонометрических функций некоторых наиболее часто встречающихся углов. Конец радиус-вектора, отвечающего углу 0°, точка , имеет координаты (1; 0). Поэтому , , , не определён. Совершенно аналогично рассматриваются точки , что даёт: Данные нами определения совпадают для острых углов с определениями тригонометрических функций в геометрии. В самом деле, например, синусом острого угла прямоугольного треугольника (см. рис. 2.4.1.4) называлось отношение противолежащего катета к гипотенузе: Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника. Однако если мы поместим наш прямоугольный треугольник так, что его вершина – точка – совпадёт с началом координат, а точка будет лежать на единичной окружности (то есть мы выбираем тем самым гипотенузу ), то геометрическое определение синуса примет вид: Значит, синус острого угла равен ординате точки, лежащей на тригонометрической окружности. А это как раз совпадает с нашим определением синуса. Совершенно те же самые рассуждения приводят нас к полной эквивалентности геометрического определения тригонометрических функций с тем, что дано в настоящем разделе. Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением. Рассмотрим правильный треугольник со стороной, равной 1. Тогда по теореме Пифагора легко найти, что длина его высоты равна Значит, Рассматривая угол найдём, что Соответственно, Рассмотрим теперь прямоугольный равнобедренный треугольник с катетами, равными , . Тогда по теореме Пифагора и Следовательно, Итак, мы вычислили значения тригонометрических функций основных углов. Составим таблицу значений тригонометрических функций, которую мы только что получили. Читайте также:
|

