Метод нелдера мида кратко

Обновлено: 02.07.2024

Ее запись на Фортране:

real(8) function Rosenbrock(X, n)
real(8) X(n)
Rosenbrock = (1.0_8 - X(1))**2 + 100.0_8 * (X(2) - X(1) * X(1) )**2
end function Rosenbrock

Глобальный минимум функции равен 0.0 и находится в точке (x1, x2) = (1.0, 1.0).
При работе с функцией Розенброка для проверки используемого метода в качестве начальной часто берут точку
(-5, 10)
или точку
(-2.048, 2.048).
Приводимые программы могут работать с произвольной оптимизируемой функцией.

Симплекс и операции с симплексом в методе Нелдера-Мида

В начале работы алгоритма Нелдера-Мида строится регулярный симплекс: в пространстве R n - это правильный многогранник, образованный n + 1 равноотстоящими друг от друга вершинами. Так, в R 2 – это равносторонний треугольник. В пространстве R n координаты вершин регулярного симплекса, в котором первая вершина
X = (x₁, x₂, . x_n),
можно задать следующей матрицей:

в которой в столбце i находятся координаты i-й вершины симплекса и

где l - длина ребра симплекса.
Так, в R 2 из вершины X = (0, 0) регулярный симплекс (рис. 1) задается следующей матрицей:

Рис. 1. R 2 -регулярный симплекс из вершины X = (0, 0)

Построение регулярного симплекса выполняет следующая подпрограмма:

! Создает из точки X регулярный симплекс с длиной ребра L и с n + 1 вершиной
! Формирует массив FN значений оптимизируемой функции F в вершинах симплекса
subroutine makeSimplex(X, L, n)
real(8) X(:), L
integer n
real(8) qn, q2, r1, r2
qn = sqrt(1.0_8 + n) - 1.0_8
q2 = L / sqrt(2.0_8) * n
r1 = q2 * (qn + n)
r2 = q2 * qn
simplex(:, 1) = X
do i = 2, n + 1
simplex(:, i) = X + r2
end do
do i = 2, n + 1
simplex(i - 1, i) = simplex(i - 1, i) - r2 + r1
end do
do i = 1, n + 1
! Значения функции в вершинах симплекса
FN(i) = F(simplex(:, i), n)
end do
end subroutine makeSimplex

В алгоритме Нелдера-Мида используются следующие симплекс-операции:

отражение (рис. 2);
редукция (рис. 3);
сжатие (рис. 4);
растяжение (рис. 5).

Рис. 2. Отражение R 2 -симплекса

Рис. 3. Редукция R 2 -симплекса

Рис. 4. Сжатие R 2 -симплекса

Рис. 5. Растяжение R 2 -симплекса

В процессе работы алгоритма после операции сжатия или растяжения симплекс преобразуется из регулярного в обычный.
Отражение вершины выполняется относительно X_c центра тяжести симплекса:

где k - номер отражаемой вершины, r - номер текущего шага алгоритма.
Координаты отраженной вершины вычисляются по следующей формуле:

Обычно cR = 1.0. Координаты прочих вершин симплекса при выполнении операции отражения не меняются.
Центр тяжести симплекса возвращается следующей функцией:

function center_of_gravity(simplex, k, n)
real(8) center_of_gravity(n)
real(8), intent(in) :: simplex(n, n + 1)
integer, intent(in) :: k, n
integer j
do j = 1, n
center_of_gravity(j) = sum(simplex(j, :))
end do
center_of_gravity = (center_of_gravity - simplex(:, k)) / n
end function center_of_gravity

Отражение вершины с номером k относительно центра тяжести симплекса обеспечивает следующая подпрограмма:

subroutine reflection(simplex, k, cR, n)
real(8) simplex(n, n + 1)
! cR – коэффициент отражения
real(8), intent(in) :: cR
integer, intent(in) :: k, n
simplex(:, k) = (1 +cR) * center_of_gravity(simplex, k, n) - simplex(:, k)
end subroutine reflection

Редукция симплекса, – уменьшение длины всех ребер симплекса, выполняется к выбранной в алгоритме вершине X_k симплекса. Новые координаты редуцированного симплекса определяются по следующей формуле:

где γ - коэффициент редукции (положительное число, меньшее 1.0; часто берется значение 0.5), r - номер текущего шага алгоритма.
За редукцию симплекса отвечает следующая подпрограмма:

subroutine reduction(simplex, k, gamma, n)
real(8) simplex(n, n + 1)
real(8), intent(in) :: gamma
integer, intent(in) :: k, n
real(8) xk(n)
integer j
xk = simplex(:, k)
do j = 1, n
simplex(:, j) = xk + gamma * (simplex(:, j) - xk)
end do
simplex(:, k) = xk
end subroutine reduction

Сжатие симплекса выполняется в направлении X_k - X_c, где X_k - выбранная в алгоритме вершина симплекса, а X_c - центр его тяжести. В результате сжатия изменяются координаты вершины X_k:

где β - коэффициент сжатия (положительное число, меньшее 1.0; нередко берется значение 0.5), r - номер текущего шага алгоритма.
Координаты прочих вершин симплекса не изменяются.
Растяжение симплекса выполняется в направлении X_k - X_c, где X_k - выбранная в алгоритме вершина, а X_c - центр его тяжести. В результате растяжения изменяются координаты вершины X_k:

где α - коэффициент растяжения (положительное число, большее 1.0; можно употребить, например, значение 2.0), r - номер текущего шага алгоритма.
Координаты прочих вершин симплекса не изменяются.
Сжатие или растяжение симплекса выполняет следующая подпрограмма:

subroutine shrinking_expansion(simplex, k, alpha_beta, n)
real(8) simplex(n, n + 1)
real(8), intent(in) :: alpha_beta
integer, intent(in) :: k, n
real(8) xc(n)
xc = center_of_gravity(simplex, k, n)
simplex(:, k) = xc + alpha_beta * (simplex(:, k) - xc)
end subroutine shrinking_expansion

В случае сильно овражных функций может происходить вырождение (сплющивание) симплекса, что приводит к необходимости восстановления симплекса, которое заключается в следующем:

в текущем симплексе выбираются две вершины с минимальными значениями оптимизируемой функции и определяется L_c расстояние между ними;
из вершины с минимальным значением функции строится новый симплекс, длина ребра которого принимается равной L_c.

Восстановление симплекса выполняет следующая подпрограмма:

! Восстанавливает симплекс
subroutine simplexRestore()
real(8) fmi
real(8) X2(n)
integer imi(1), imi2(1)
fmi = minval(fn)
imi = minloc(fn)
imi2 = minloc(fn, fn /= fmi)
X2 = simplex(:, imi(1)) - simplex(:, imi2(1))
call makeSimplex(simplex(:, imi(1)), sqrt(dot_product(X2, X2)), n)
end subroutine simplexRestore

Алгоритм метода Нелдера-Мида

Начало.
Задать начальную точку X = (x₁, x₂, …, x_n) и n – размер вектора X.
Задать L и L_thres соответственно начальное и наименьшее значения длины ребра симплекса.
Задать cR, alpha, beta и gamma соответственно коэффициенты отражения, растяжения, сжатия и редукции симплекса.
Простроить из точки X регулярный симплекса с длиной ребра L и числом вершин n + 1.
Вычислить значения функции в вершинах начального симплекса.
Пока в симплексе есть ребро, длина которого больше L_thres
Найти в симплексе вершину k, в которой значение функции максимально (Fma).
Найти Fmi – минимальное значение функции в текущем симплексе.
Выполнить отражение вершины k и найти F_R – значение функции в отраженной вершине.
Если F_R > Fma Тогда
Выполнить, перемещая вершину k, сжатие симплекса и найти F_S – значение функции в вершине k после сжатия.
Если F_R > Fma Тогда
Вернуться к симплексу до отражения и выполнить его редукцию, сохраняя положение вершины k.
Вычислить значения функции в вершинах редуцированного симплекса.
Иначе
Продолжить работу со сжатым симплексом.
Конец Если
Иначе Если F_R Fmi Тогда
Отказаться от растяжения и продолжить работу с симплексом, полученным после отражения.
Иначе
Продолжить работу с симплексом, полученным после растяжения.
Конец Если
Конец Если
Конец Цикла
Напечатать в качестве результата координаты вершины симплекса с минимальным значением функции.
Останов.

Фортран-реализация метода Нелдера-Мида

В главной программе задаются параметры алгоритма и начальный симплекс (регулярный). Оптимизируемая функция объявляется в главной программе с атрибутом External и поэтому может быть использована в качестве параметра процедуры.

program tst
integer, parameter :: n = 2
real(8) X(n), L, L_thres, cR, alpha, beta, gamma
real(8), external :: Rosenbrock
L = 0.4_8 ! Начальная длина ребра симплекса
L_thres = 1.0e-5_8 ! Предельное значение длины ребра симплекса
cR = 1.0_8 ! Коэффициент отражения симплекса
alpha = 2.0_8 ! Коэффициент растяжения симплекса
beta = 0.5_8 ! Коэффициент сжатия симплекса
gamma = 0.5_8 ! Коэффициент редукции симплекса
! Первая вершина начального симплекса (начальная точка)
X(1) = 5.0_8
X(2) = -5.0_8
print *, 'Start point = ', X
!
! Поиск минимума функции Розенброка
call nelMead(Rosenbrock, X, n, L, L_thres, cR, alpha, beta, gamma)
!
! Результат
print *, 'Result = ', X
end program tst
!
! Выполняет поиск экстремума (минимума) функции F
subroutine nelMead(F, X, n, L, L_thres, cR, alpha, beta, gamma)
real(8) F, X(n), L, L_thres, cR, alpha, beta, gamma
integer n, j, jMx, i
real(8) X_R(n), simplex(n, n + 1), FN(n + 1)
real(8) Fmi, Fma, F_R, F_S, F_E
integer ima(1), k, kr
! kr_todo - число шагов алгоритма, после выполнения которых симплекс восстанавливается
integer, parameter :: kr_todo = 60
j = 0
! Предельное число шагов алгоритма (убрать после отладки)
jMx = 10000
print *, 'L = ', L
print *, 'L_thres = ', L_thres
print *, 'cR = ', cR
print *, 'alpha = ', alpha
print *, 'beta = ', beta
print *, 'gamma = ', gamma
call makeSimplex(X, L, n)
kr = 0
k = 1
do while (notStopYet() .and. j Fma) then
! Сжатие
call shrinking_expansion(simplex, k, beta, n)
! Значение функции в вершине k симплекса после его сжатия
F_S = F(simplex(:, k), n)
if (F_S > Fma) then
simplex(:, k) = X
! Редукция
call reduction(simplex, k, gamma, n)
do i = 1, n + 1
if (i == k) cycle
! Значения функций в вершинах симплекса после редукции
! В вершине k значение функции сохраняется
FN(i) = F(simplex(:, i), n)
end do
else
FN(k) = F_S
end if
else if (F_R Fmi) then
simplex(:, k) = X_R
FN(k) = F_R
else
FN(k) = F_E
end if
else
FN(k) = F_R
end if
end do
! Результат
print *, 'Number of iterations j = ', j
contains
!
! Возвращает .true., если длина хотя бы одного ребра симплекса превышает L_thres,
! или .false. - в противном случае
logical function notStopYet()
integer i, j
real(8) X(n), X2(n)
notStopYet = .false.
do i = 1, n
X = simplex(:, i)
do j = i + 1, n + 1
X2 = X - simplex(:, j)
if (sqrt(dot_product(X2, X2)) > L_thres) then
notStopYet = .true.
return
end if
end do
end do
end function notStopYet
!
! Второй вариант определения точки останова алгоритма
! Возвращает .true., если хотя бы одна разница значений функций в вершинах симплекса превышает L_thres,
! или .false. - в противном случае
logical function notStopYet2()
integer i, j
real(8) fv
notStopYet2 = .false.
do i = 1, n
fv = FN(i)
do j = i + 1, n + 1
if (abs(fv - FN(j)) > L_thres) then
notStopYet2 = .true.
return
end if
end do
end do
end function notStopYet2
!
! Восстанавливает симплекс
subroutine simplexRestore()
real(8) fmi
real(8) X2(n)
integer imi(1), imi2(1)
fmi = minval(fn)
imi = minloc(fn)
imi2 = minloc(fn, fn /= fmi)
X2 = simplex(:, imi(1)) - simplex(:, imi2(1))
call makeSimplex(simplex(:, imi(1)), sqrt(dot_product(X2, X2)), n)
end subroutine simplexRestore
!
! Создает из точки X регулярный симплекс с длиной ребра L и с n + 1 вершиной
subroutine makeSimplex(X, L, n)
real(8) X(:), L
integer n
real(8) qn, q2, r1, r2
qn = sqrt(1.0_8 + n) - 1.0_8
q2 = L / sqrt(2.0_8) * n
r1 = q2 * (qn + n)
r2 = q2 * qn
simplex(:, 1) = X
do i = 2, n + 1
simplex(:, i) = X + r2
end do
do i = 2, n + 1
simplex(i - 1, i) = simplex(i - 1, i) - r2 + r1
end do
do i = 1, n + 1
! Значения функции в вершинах созданного симплекса
FN(i) = F(simplex(:, i), n)
end do
end subroutine makeSimplex
!
! Вычисляет центр тяжести симплекса
function center_of_gravity(simplex, k, n)
real(8) center_of_gravity(n)
real(8), intent(in) :: simplex(n, n + 1)
integer, intent(in) :: k, n
integer j
do j = 1, n
center_of_gravity(j) = sum(simplex(j, :))
end do
center_of_gravity = (center_of_gravity - simplex(:, k)) / n
end function center_of_gravity
!
! Выполняет операцию отражения
subroutine reflection(simplex, k, cR, n)
real(8) simplex(n, n + 1)
! cR - коэффициент отражения
real(8), intent(in) :: cR
integer, intent(in) :: k, n
simplex(:, k) = (1 +cR) * center_of_gravity(simplex, k, n) - simplex(:, k)
end subroutine reflection
!
! Обеспечивает редукцию симплекса
subroutine reduction(simplex, k, gamma, n)
real(8) simplex(n, n + 1)
real(8), intent(in) :: gamma
integer, intent(in) :: k, n
real(8) xk(n)
integer j
xk = simplex(:, k)
do j = 1, n
simplex(:, j) = xk + gamma * (simplex(:, j) - xk)
end do
simplex(:, k) = xk
end subroutine reduction
!
! Растяжение или сжатие симплекса
subroutine shrinking_expansion(simplex, k, alpha_beta, n)
real(8) simplex(n, n + 1)
real(8), intent(in) :: alpha_beta
integer, intent(in) :: k, n
real(8) xc(n)
xc = center_of_gravity(simplex, k, n)
simplex(:, k) = xc + alpha_beta * (simplex(:, k) - xc)
end subroutine shrinking_expansion
end subroutine nelMead
!
real(8) function Rosenbrock(X, n)
real(8) X(n)
integer n
Rosenbrock = (1.0_8 - X(1))**2 + 100.0_8 * (X(2) - X(1) * X(1) )**2
end function Rosenbrock

Второй вариант определения точки останова алгоритма реализуется функцией notStopYet2, которая возвращает .true., если хотя бы одна разница значений функций в различных вершинах симплекса превышает L_thres. В противном случае функция вернет .false.

using System;
using System.IO; // StreamReader
using System.Windows.Forms;

namespace WindowsFormsApplicationNelderMid
public partial class FormNelderMid : Form
const int NP = 2; // NP - число аргументов функции
double[,] simplex = new double[NP, NP + 1]; // NP + 1 - число вершин симплекса
double[] FN = new double[NP + 1];
StreamWriter sW = new StreamWriter("res.txt");

public FormNelderMid()
InitializeComponent();
>
private double F(double[] X, int NP) // Функциия Розенброка
double x1 = X[0];
double p = 1.0 - x1;
double p2 = X[1] - x1 * x1;
return p * p + 100.0 * p2 * p2;
>
// Создает из точки X регулярный симплекс с длиной ребра L и с NP + 1 вершиной
// Формирует массив FN значений оптимизируемой функции F в вершинах симплекса
private void makeSimplex(double[] X, double L, int NP, bool first)
double qn, q2, r1, r2;
int i, j;
qn = Math.Sqrt(1.0 + NP) - 1.0;
q2 = L / Math.Sqrt(2.0) * (double)NP;
r1 = q2 * (qn + (double)NP);
r2 = q2 * qn;
for(i = 0; i fma)
fma = f;
ima = i;
>
>
return fma;
>
private void simplexRestore(int NP) // Восстанавление симплекса
int i, imi = -1, imi2 = -1;
double fmi, fmi2 = double.MaxValue, f;
double[] X = new double[NP], X2 = new double[NP];
fmi = minval(FN, NP + 1, ref imi);
for (i = 0; i L_thres) return true;
>
>
return false;
>
// Выполняет поиск экстремума (минимума) функции F
private void nelMead(ref double[] X, int NP, double L, double L_thres, double cR, double alpha, double beta, double gamma)
int i, j2, imi = -1, ima = -1;
int j = 0, kr = 0, jMx = 10000; // Предельное число шагов алгоритма (убрать после отладки)
double[] X2 = new double[NP], X_R = new double[NP];
double Fmi, Fma, F_R, F_S, F_E;
const int kr_todo = 60; // kr_todo - число шагов алгоритма, после выполнения которых симплекс восстанавливается
sW.WriteLine("L L_thres cR alpha beta gamma Число итераций: " + j);
>
private void Go_Click(object sender, EventArgs e)
// -2.048, 2.048
// -5.0, 10.0
double[] X = < -2.048, 2.048 >; // Первая вершина начального симплекса (начальная точка)
double L, L_thres, cR, alpha, beta, gamma;
L = 0.4; // Начальная длина ребра симплекса
L_thres = 1.0e-5; // Предельное значение длины ребра симплекса
cR = 1.0; // Коэффициент отражения симплекса
alpha = 2.0; // Коэффициент растяжения симплекса
beta = 0.5; // Коэффициент сжатия симплекса
gamma = 0.5; // Коэффициент редукции симплекса
sW.WriteLine("Начальная точка:"); // Результат
for (int i = 0; i < NP; i++) sW.WriteLine(X[i]);
nelMead(ref X, NP, L, L_thres, cR, alpha, beta, gamma); // Поиск минимума функции Розенброка
sW.WriteLine("Результат:");
sW.WriteLine("Аргументы:");
for (int i = 0; i < NP; i++) sW.WriteLine(X[i]);
sW.WriteLine("Функция в вершинах симплекса:");
for (int i = 0; i < NP + 1; i++) sW.WriteLine(FN[i]);
sW.Close();
MessageBox.Show("Готово");
>
private void buttonClose_Click(object sender, EventArgs e)
Close();
>
>
>

Python-реализация метода Нелдера-Мида

Используется библиотека SciPy [2]. Реализуются два варианта вызова библиотечной процедуры оптимизации:

Задается начальная точка поиска минимума функции.
Задается начальный симплекс поиска минимума функции.

Результат:
final_simplex: (array([[0.99999804, 0.99999609],
[1.00000156, 1.0000033 ],
[1.00000214, 1.00000398]]), array([3.84730933e-12, 5.66678063e-12, 1.41233808e-11]))
fun: 3.847309326090408e-12
message: 'Optimization terminated successfully.'
nfev: 135
nit: 70
status: 0
success: True
x: array([0.99999804, 0.99999609])

Результат:
final_simplex: (array([[0.99999847, 0.99999698],
[1.00000191, 1.00000346],
[0.99999669, 0.99999303]]), array([2.47098051e-12, 1.69748815e-11, 2.25735805e-11]))
fun: 2.4709805087558158e-12
message: 'Optimization terminated successfully.'
nfev: 158
nit: 83
status: 0
success: True
x: array([0.99999847, 0.99999698])

Заключение

При испытании программы поиск минимума функции Розенброка начинался с различных точек. Во всех случаях минимум был обнаружен.
Точность поиска равна 1.0e-5.
Точки брались следующие:

Метод Нелдера-Мида является развитием симплексного метода Спендли, Хекста и Химсворта. Выпуклая оболочка множества -й равноудаленной точки в -мерном пространстве называется регулярным симплексом. Эта конфигурация рассматривается в методе Спендли, Хекста и Химсворта. В двухмерном пространстве регулярным симплексом является правильный треугольник, а в трехмерном - правильный тетраэдр. Идея метода состоит в сравнении значений функции в вершинах симплекса и перемещении симплекса в направлении оптимальной точки с помощью итерационной процедуры. В симплексном методе, предложенном первоначально, регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько модификаций этого метода, допускающих, чтобы симплексы были неправильными. В результате получился очень надежный метод прямого поиска, являющийся одним из самых эффективных при .

Главными особенностями алгоритма можно назвать следующие:

Метод Нелдера-Мида не накладывает ограничений на гладкость функции
Данный метод явялется эффективным при низкой скорости вычисления минимизируемой функции. Как правило, на каждой итерации происходит вычисление значения функции не более чем в 3 точках.
Отсутствие теории сходимости. АЛгоритм может расходиться даже на гладких функциях.

Постановка математической задачи

Задачей оптимизации называется задача поиска экстремума функции, заданной на некотором множетсве.

Как правило, под задачей оптимизации также подразумевается поиск элемента , при котором целевая функция достигает экстремума.

Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

Допустимое множество
Целевую функцию
Критерий поиска (max или min)

Тогда решить задачу означает одно из:

Показать что
Показать, что целевая функция не ограничена.
Найти
Если не существует , то найти

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Рассматриваемая задача

Метод Нелдера-Мида, также известный как метод деформируемого многогранника, — метод безусловной оптимизации вещественной функции от нескольких переменных. Иными словами на допустимое множество накладываются следующие ограничения:

Кроме того, одним из главных преимуществ данного метода является то, что в нем не используется градиента целевой функции, что позволяет применять его к негладким функциям. Метод Нелдера-Мида использует понятие симплекса -мерного пространства'.

Множество называется выпуклым, если .

Выпуклой оболочкой множества называется наименьшее выпуклое множество такое, что

Симплексом или -симплексом называется выпуклая оболочка множества точек.

1-симплексом является отрезок

2-симплексом является треугольник

3-симплексом является тетраэдр.

Изложение метода

Параметрами метода являются:

коэффициент отражения , обычно выбирается равным 1.
коэффициент сжатия , обычно выбирается равным 0.5.
коэффициент растяжения , обычно выбирается равным 2.

Инициализация.Произвольным образом выбирается точка , образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: .

1. Сортировка. Из вершин симплекса выбираем три точки: с наибольшим (из выбранных) значением функции , со следующим по величине значением и с наименьшим значением функции . Целью дальнейших манипуляций будет уменьшение по крайней мере . 2. Найдём центр тяжести всех точек, за исключением . Вычислять не обязательно. 3. Отражение. Отразим точку относительно с коэффициентом (при это будет центральная симметрия, в общем случае — гомотетия), получим точку и вычислим в ней функцию: . Координаты новой точки вычисляются по формуле 4. Далее сравниваем значение со значениями : 4а. Если , то производим растяжение. Новая точка и значение функции . Если , то заменяем точку на и заканчиваем итерацию (на шаг 8). Если , то заменяем точку на и заканчиваем итерацию (на шаг 8). 4b. Если , то заменяем точку на и переходим на шаг 8. 4с. Если , то меняем обозначения (и соответствующие значения функции) местами и переходим на шаг 5. 4d. Если , то переходим на шаг 5. 5. Сжатие. Строим точку и вычисляем в ней значение . 6. Если , то заменяем точку на и переходим на шаг 8. 7. Если , то производим сжатие симплекса — гомотетию к точке с наименьшим значением : для всех требуемых точек . 8. Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 1.

Анализ метода

Изучение сходимости алгоритма Нелдера-Мида является трудной математической задачей. Известные результаты о сходимости симплекс-методов основаны на следующих предположениях:

Симплекс не должен вырождаться при итерациях алгоритма

На гладкость функции накладываются некоторые условия

В общем случае для метода Нелдера-Мида не выполняются сразу оба эти предположения, а следовательно, об условиях сходимости известно весьма мало. МакКиннон в 1998 году описал семейство строго выпуклых функций и класс начальных симплексов в двухмерном пространстве, для которых все вершины рабочего симплекса сходятся не к оптимальной точке. В 1998 году Лагариас опубликовал статью, в которой он исследовал сходимость метода в одно- и двухмерном пространствах для некоторых строго выпуклых функций с ограниченными поверхностями уровня.

Алгоритм Нелдера-Мида дает сильное уменьшение значение функции уже при первых нескольких итерациях и быстро достигает необходимой точности. Как правило, алгоритм производит одно или два вычисления функции на каждой итерации, если не учитывать сжатие, которое редко используется на практике. Это крайне важно в тех ситуациях, когда вычисление значений функции очень дорого или же требует много времени. Для подобных задач алгоритм Нелдера-Мида гораздо эффективнее многих других методов, требующих вычисления не менее значений функции на каждой итерации.

Главными преимуществами алгоритма являются его простота и эффективность.

С другой стороны, в силу отсутствия теории сходимости, на практике метод может приводить к неверному ответу даже для гладких функций. Также возможна ситуация, когда рабочий симплекс находится далеко от оптимальной точки, а алгоритм производит большое число итерации, при этом мало изменяя значения функции. Эвристический метод решения этой проблемы заключается в запуске алгоритма несколько раз и ограничении числа итераций.

Числовой эксперимент

В качестве числового эксперимента метод Нелдера-Мида был применен для вычисления минимума функции Розенброка:

для которой и . В качестве начального прибилжения был взят симплекс .

Ниже приведена таблица промежуточных результатов после каждых 10 итераций алгоритма.

Число итераций	Координаты первой точки симплекса	Координаты второй точки симплекса	Координаты третьей точки симплекса
10	x=2.78; y=7.55;	x=2.39; y=6.39;	x=1.73; y=6.87;	6.725	1479.400
20	x=2.63; y=6.96;	x=2.70; y=7.29;	x=2.64; y=6.88;	2.769	3.225
30	x=2.24; y=4.94;	x=2.35; y=5.50;	x=2.42; y=5.86;	1.823	2.017
40	x=1.90; y=3.58;	x=1.83; y=3.38;	x=1.97; y=3.89;	0.821	0.996
50	x=1.51; y=2.28;	x=1.53; y=2.36;	x=1.57; y=2.47;	0.273	0.327
60	x=1.20; y=1.42;	x=1.23; y=1.51;	x=1.27; y=1.61;	0.050	0.079
70	x=0.99; y=0.97;	x=1.01; y=1.02;	x=0.96; y=0.93;	0.000	0.003

Итоговое количество итераций 79. Вычисленный минимум функционала равен .

Заключение

Симплекс-метод Нелдера-Мида является очень эффективным алгоритмом поиска экстремума функции многих переменных, не накладывающим ограничений на гладкость функции. На каждой итерации алгоритма производится как правило одно-два вычисления значений функции, что чрезвычайно эффективно если эти вычисления очень медленны. Кроме того, алгоритма очень прост в реализации. Главным же его недостатком является отсутствие теории сходимости и наличие примеров, когда метод расходится даже на гладких функциях.

Метод Нелдера — Мида — метод оптимизации (поиска минимума) функции от нескольких переменных. Простой и в тоже время эффективный метод, позволяющий оптимизировать функции без использования градиентов. Метод надежен и, как правило, показывает хорошие результаты, хотя и отсутствует теория сходимости. Может использоваться в функции optimize из модуля scipy.optimize популярной библиотеки для языка python, которая используется для математических расчетов.

Алгоритм заключается в формировании симплекса (simplex) и последующего его деформирования в направлении минимума, посредством трех операций:

1) Отражение (reflection);
2) Растяжение (expansion);
3) Сжатие (contract);

Симплекс представляет из себя геометрическую фигуру, являющуюся n — мерным обобщением треугольника. Для одномерного пространства — это отрезок, для двумерного — треугольник. Таким образом n — мерный симплекс имеет n + 1 вершину.

Алгоритм

1) Пусть функция, которую необходимо оптимизировать. На первом шаге выбираем три случайные точки (об этом чуть позже) и формируем симплекс (треугольник). Вычисляем значение функции в каждой точке: , , .

Сортируем точки по значениям функции в этих точках, таким образом получаем двойное неравенство:

Мы ищем минимум функции, а следовательно, на данном шаге лучшей будет та точка, в которой значение функции минимально. Для удобства переобозначим точки следующим образом:

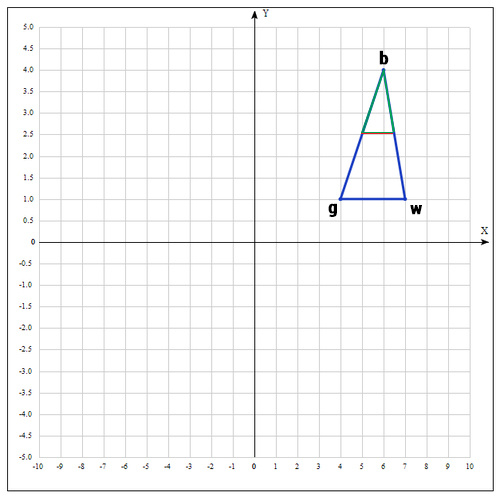
b = , g = , w = , где best, good, worst — соответственно.

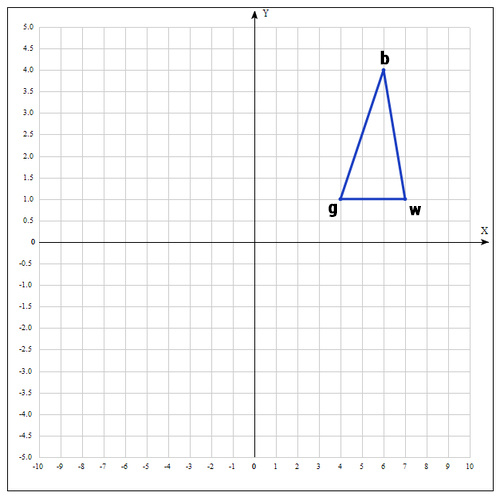
2) На следующем шаге находим середину отрезка, точками которого являются g и b. Т.к. координаты середины отрезка равны полусумме координат его концов, получаем:

В более общем виде можно записать так:

3) Применяем операцию отражения:
Находим точку , следующим образом:

Т.е. фактически отражаем точку w относительно mid. В качестве коэффициента берут как правило 1. Проверяем нашу точку: если , то это хорошая точка. А теперь попробуем расстояние увеличить в 2 раза, вдруг нам повезет и мы найдем точку еще лучше.

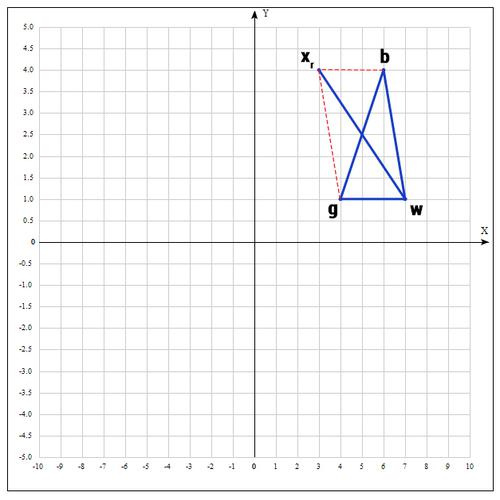
4) Применяем операцию растяжения:
Находим точку следующим образом:

В качестве γ принимаем γ = 2, т.е. расстояние увеличиваем в 2 раза.

Если , то нам повезло и мы нашли точку лучше, чем есть на данный момент, если бы этого не произошло, мы бы остановились на точке .

Далее заменяем точку w на , в итоге получаем:

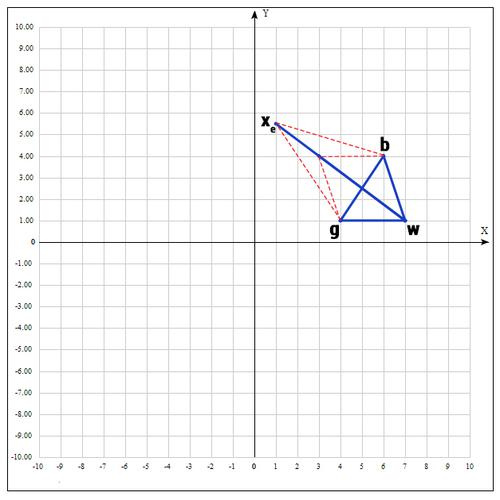
5) Если же нам совсем не повезло и мы не нашли хороших точек, пробуем операцию сжатия.
Как следует из названия операции мы будем уменьшать наш отрезок и искать хорошие точки внутри треугольника.

Пробуем найти хорошую точку :

Коэффициент β принимаем равным 0.5, т.е. точка на середине отрезка wmid.

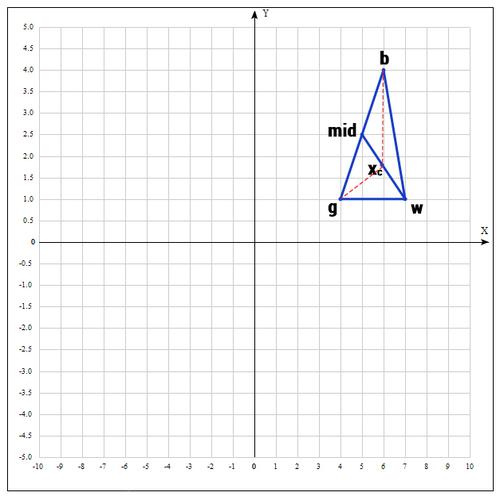
Коэффициент δ берут равным 0.5.

Необходимо отметить, что данная операция дорого обходится, поскольку необходимо заменять точки в симплексе. К счастью было установлено, при проведении большого количества экспериментов, что shrink — трансформация редко случается на практике.

Алгоритм заканчивается, когда:

1) Было выполнено необходимое количество итераций.
2) Площадь симплекса достигла определенной величины.
3) Текущее лучшее решение достигло необходимой точности.

Как и в большинстве эвристических методов, не существует идеального способа выбора инициализирующих точек. Как уже было сказано, можно брать случайные точки, находящиеся недалеко друг от друга для формирования симплекса; но есть решение и получше, которое используется в реализации алгоритма в MATHLAB:

Выбор первой точки поручаем пользователю, если он имеет некоторое представление о возможном хорошем решении, в противном случае выбирается случайным образом. Остальные точки выбираются исходя из , на небольшом расстоянии вдоль направления каждого измерения:

где — единичный вектор.
определяется таким образом:
= 0.05, если коэффициент при в определении не нулевой.
= 0.00025, если коэффициент при в определении нулевой.

Пример:

Найти экстремум следующей функции:

В качестве начальных возьмем точки:

Вычислим значение функции в каждой точке:

Переобозначим точки следующим образом:

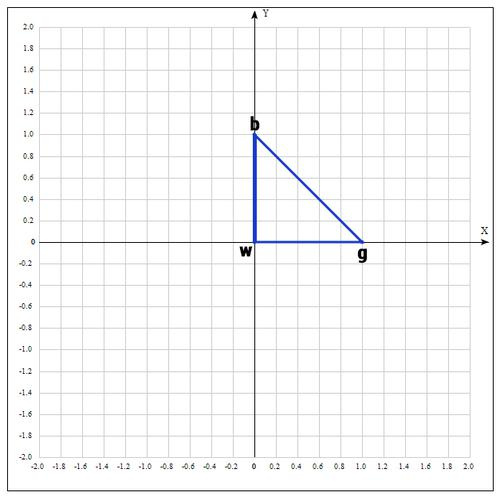
Находим середину отрезка bg:

Находим точку (операция отражения):

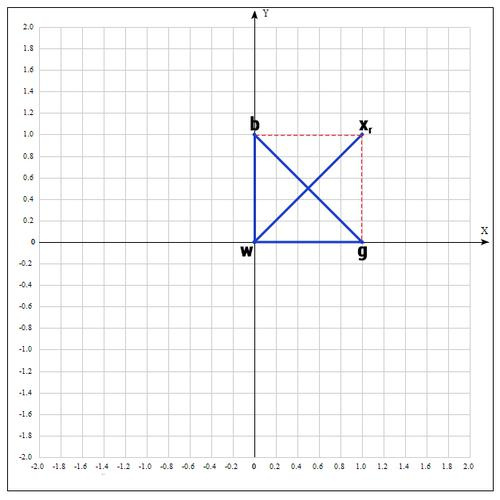
, т.к. пробуем увеличить отрезок (операция растяжения).

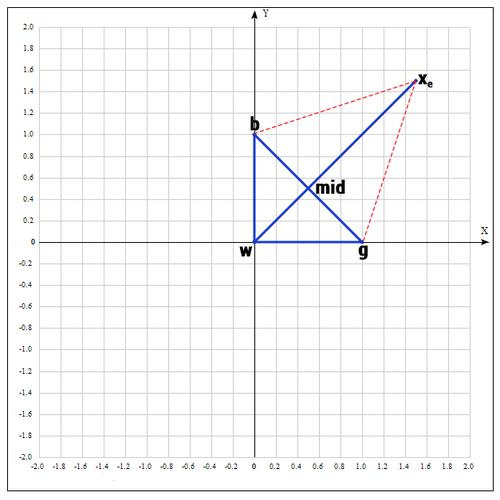
Проверяем значение функции в точке :

И алгоритм начинается сначала.

Таблица значений для 10 итераций:

Best	Good	Worst

Аналитически находим экстремум функции, он достигается в точке .
После 10 итераций мы получаем достаточно точное приближение:

Еще о методе:

Алгоритм Нелдера — Мида в основном используется для выбора параметра в машинном обучении. В сущности, симплекс-метод используется для оптимизации параметров модели. Это связано с тем, что данный метод оптимизирует целевую функцию довольно быстро и эффективно (особенно там, где не используется shrink — модификация).

С другой стороны, в силу отсутствия теории сходимости, на практике метод может приводить к неверному ответу даже на гладких (непрерывно дифференцируемых) функциях. Также возможна ситуация, когда рабочий симплекс находится далеко от оптимальной точки, а алгоритм производит большое число итераций, при этом мало изменяя значения функции. Эвристический метод решения этой проблемы заключается в запуске алгоритма несколько раз и ограничении числа итераций.

Реализация на языке программирования python:

Создаем вспомогательный класс Vector и перегружаем операторы для возможности производить с векторами базовые операции. Я намерено не использовал вспомогательные библиотеки для реализации алгоритма, т.к. в таком случае зачастую снижается восприятие.

Спасибо за чтение статьи. Надеюсь она была Вам полезна и Вы узнали много нового.
С вами был FUNNYDMAN. Удачной оптимизации!)

Минимальный поиск Нелдера – Мида Функция Симионеску. Вершины симплекса упорядочены по их значению, причем 1 имеет наименьшее (лучшее) значение.

В Метод Нелдера – Мида (также односторонний спуск, метод амебы, или же многогранник) широко применяется численный метод используется для нахождения минимума или максимума целевая функция в многомерном пространстве. Это метод прямого поиска (основан на сравнении функций) и часто применяется к нелинейным оптимизация проблемы, для которых производные могут быть неизвестны. Однако метод Нелдера – Мида - это эвристический метод поиска, который может сходиться к нестационарным точкам [1] о проблемах, которые можно решить альтернативными методами. [2]

Техника Нелдера – Мида была предложена Джон Нелдер и Роджер Мид в 1965 г., [3] как развитие метода Spendley et al. [4]

Содержание

Обзор

В методе используется концепция симплекс, что является особенным многогранник из п + 1 вершина в п Габаритные размеры. Примеры симплексов включают отрезок на прямой, треугольник на плоскости, тетраэдр в трехмерном пространстве и так далее.

Метод аппроксимирует локальный оптимум задачи с п переменных, когда целевая функция изменяется плавно и одномодальный. Типичные реализации минимизируют функции, а мы максимизируем ж ( Икс ) < Displaystyle е ( mathbf )> минимизируя − ж ( Икс ) < Displaystyle -f ( mathbf )> .

Например, инженер по подвесному мосту должен выбрать толщину каждой стойки, троса и опоры. Эти элементы взаимозависимы, но непросто представить себе влияние изменения какого-либо конкретного элемента. Моделирование таких сложных структур часто требует чрезвычайно больших вычислительных затрат и, возможно, занимает более часов на выполнение. Метод Нелдера – Мида в исходном варианте требует не более двух вычислений на итерацию, за исключением сокращаться описанная ниже операция, которая привлекательна по сравнению с некоторыми другими методами оптимизации прямого поиска. Однако общее количество итераций до предложенного оптимума может быть большим.

В отличие от современных методов оптимизации, эвристика Нелдера – Мида может сходиться к нестационарной точке, если только задача не удовлетворяет более строгим условиям, чем это необходимо для современных методов. [1] Современные усовершенствования эвристики Нелдера – Мида известны с 1979 года. [2]

Существует множество вариаций, зависящих от реальной природы решаемой проблемы. В распространенном варианте используется небольшой симплекс постоянного размера, который примерно следует направлению градиента (что дает крутой спуск). Визуализируйте маленький треугольник на карте высот, переворачивающийся вниз по долине к местному дну. Этот метод также известен как метод гибкого многогранника. Это, однако, имеет тенденцию плохо работать по сравнению с методом, описанным в этой статье, поскольку он выполняет небольшие ненужные шаги в областях, которые не представляют особого интереса.

Один из возможных вариантов алгоритма NM

(Это примерно соответствует процедуре, описанной в исходной статье Нелдера – Мида.)

Nelder-Мид является алгоритм для оптимизации нелинейных который был опубликован Джон Nelder и Роджер Мид (в) в 1965 году . Это эвристический численный метод, который стремится минимизировать непрерывную функцию в пространстве с несколькими измерениями.

Алгоритм, также называемый симплекс-методом спуска , использует концепцию симплекса, который представляет собой многогранник из N +1 вершин в N- мерном пространстве . Начиная с такого симплекса, он претерпевает простые преобразования во время итераций : он деформируется, перемещается и постепенно сокращается, пока его вершины не приблизятся к точке, где функция локально минимальна.

Метод Нелдера-Мида с моделированием отжига является результатом связи между исходным алгоритмом и эмпирическим механизмом моделирования отжига .

Резюме

Алгоритм

Является ли функция F , определенная на пространстве размерности N . Алгоритм начинается с определения невырожденного симплекса, выбранного в этом пространстве. Путь последовательных итераций , процесс состоит в определении точки симплекса где функция является максимальной для того , чтобы заменить его отражение (т.е. симметричного) эту точку относительно центра тяжести N остальных точек . Если значение функции в этой новой точке меньше, чем все другие значения, взятые в других точках, симплекс растягивается в этом направлении. В противном случае, если значение функции в этой новой точке лучше, чем вторая, хуже, но хуже, чем лучшее, мы сохраняем это значение и начинаем заново. В противном случае предполагается, что локальная форма функции представляет собой долину, а симплекс сжимается сам по себе. Если это все еще не дает лучшего результата, симплекс сокращается на гомотетию с центром в точке симплекса, где функция минимальна.

Выбор N + 1 точек в пространстве неизвестной размерности N . Это формирует симплекс: < >, Икс 1 , Икс 2 , . . . , Икс НЕТ + 1 , x_ , . x_ >
Вычисление значений функции f в этих точках, сортировка точек по имеющимся . На самом деле достаточно знать первое и два последних. ж ( Икс 1 ) ≤ ж ( Икс 2 ) ≤ . . . ≤ ж ( Икс НЕТ + 1 ) ) \ leq f (x_ ) \ leq . \ leq f (x_ )>
Расчет x₀ , центра тяжести всех точек, кроме x_{N +1} .
Расчет (отражение x_N₊₁ относительно x₀ ). Икс р знак равно Икс 0 + α ( Икс 0 - Икс НЕТ + 1 ) = x_ + \ alpha (x_ -x_ )>
Или замените x_N₊₁ на и вернитесь к шагу 2. ж ( Икс 1 ) ≤ ж ( Икс р ) ж ( Икс НЕТ ) ) \ leq f (x_ ) Икс р >
То есть расчет (расширение симплекса). Если заменить x_N₊₁ на иначе, заменить x_N₊₁ на x _r и вернуться к шагу 2. ж ( Икс р ) ж ( Икс 1 ) <\ Displaystyle f (x_ ) Икс е знак равно Икс 0 + γ ( Икс р - Икс 0 ) = x_ + \ gamma (x_ -x_ )> ж ( Икс е ) ≤ ж ( Икс р ) ) \ leq f (x_ )> Икс е >
То есть расчет (сокращение симплекса). Если замените x_N₊₁ на x _c и вернитесь к шагу 2, в противном случае перейдите к шагу 8. ж ( Икс р ) ≥ ж ( Икс НЕТ ) <\ Displaystyle f (x_ ) \ geq f (x_ )> Икс против знак равно Икс 0 + ρ ( Икс НЕТ + 1 - Икс 0 ) = x_ + \ rho (x_ -x_ )> ж ( Икс против ) ж ( Икс НЕТ + 1 ) )
Гомотетия отношения и центра x₁ : замена x _i на и возврат к шагу 2. σ Икс 1 + σ ( Икс я - Икс 1 ) + \ sigma (x_ -x_ )>

Анализ

Преимущества

Общность: метод применяется к непрерывной функции без необходимости оценивать ее производные.

Простота реализации.

Эффективность для невыводимой функции.

Основополагающая геометрическая интерпретация.

Обеспечение получения убывающей серии значений.

Недостатки

Простое и очень эффективное улучшение: перезапустите алгоритм

Для преодоления недостатков 1) и 4), а также других, перезапуск алгоритма Нелдера-Мида из последнего полученного решения (и продолжение его перезапуска до тех пор, пока не будет больше улучшения, с заданной точностью), можно только улучшить (иногда очень сильно) окончательное решение. Таким же образом часто рекомендуется выполнить несколько запусков алгоритма, начиная с разных начальных решений (опять же, чтобы уменьшить влияние недостатков метода и дать возможность найти лучшее окончательное решение).

Когда область определения допускает границу и минимум расположен на этой границе или около нее, последовательные деформации симплекса имеют тенденцию к его вырождению. Эффективный способ избежать этого - расширить функцию за ее границу, добавив штраф.

Метод Нелдера-Мида с имитацией отжига

Читайте также:


Рейтинг методических объединений в школе

Инструкция по охране труда с при работе с мясорубкой в доу

Сколько детей должно быть в группе в детском саду если есть ребенок инвалид

Роль наполнителей в пластмассах кратко

История тюменской области кратко

Метод нелдера мида кратко

Симплекс и операции с симплексом в методе Нелдера-Мида

Алгоритм метода Нелдера-Мида

Фортран-реализация метода Нелдера-Мида

Python-реализация метода Нелдера-Мида

Заключение

Постановка математической задачи

Рассматриваемая задача

Изложение метода

Анализ метода

Числовой эксперимент

Рекомендации программисту

Заключение

Алгоритм

Пример:

Еще о методе:

Реализация на языке программирования python:

Содержание

Обзор

Один из возможных вариантов алгоритма NM

Резюме

Алгоритм

Анализ

Преимущества

Недостатки

Простое и очень эффективное улучшение: перезапустите алгоритм

Метод Нелдера-Мида с имитацией отжига