Составление и решение уравнений линейной регрессии доклад

Обновлено: 17.05.2024

Для исследования стохастических связей широко используется метод сопоставления двух параллельных рядов, метод аналитических группировок, корреляционный анализ, регрессионный анализ и некоторые непараметрические методы. В общем виде задача статистики в области изучения взаимосвязей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на результативный. Для ее решения применяют методы корреляционного и регрессионного анализа.

ГЛАВА 1. УРАВНЕНИЕ РЕГРЕССИИ: ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

1.1. Уравнение регрессии: сущность и типы функций

Регрессия (лат. regressio - обратное движение, переход от более сложных форм развития к менее сложным) - одно из основных понятий в теории вероятности и математической статистике, выражающее зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин. Это понятие введено Фрэнсисом Гальтоном в 1886. [9]

Теоретическая линия регрессии - это та линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи. [2, с.256]

y=f(x) - уравнение регрессии - это формула статистической связи между переменными.

Прямая линия на плоскости (в пространстве двух измерений) задается уравнением y=a+b*х. Более подробно: переменная y может быть выражена через константу (a) и угловой коэффициент (b), умноженный на переменную x. Константу иногда называют также свободным членом, а угловой коэффициент - регрессионным или B-коэффициентом. [8]

Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Главным основанием должен служить содержательный анализ природы изучаемой зависимости, ее механизма. Вместе с тем теоретически обосновать форму связи каждого из факторов с результативным показателем можно далеко не всегда, поскольку исследуемые социально-экономические явления очень сложны и факторы, формирующие их уровень, тесно переплетаются и взаимодействуют друг с другом. Поэтому на основе теоретического анализа нередко могут быть сделаны самые общие выводы относительно направления связи, возможности его изменения в исследуемой совокупности, правомерности использования линейной зависимости, возможного наличия экстремальных значений и т.п. Необходимым дополнением такого рода предположений должен быть анализ конкретных фактических данных.

Приблизительно представление о линии связи можно получить на основе эмпирической линии регрессии. Эмпирическая линия регрессии обычно является ломанной линией, имеет более или менее значительный излом. Объясняется это тем, что влияние прочих неучтенных факторов, оказывающих воздействие на вариацию результативного признака, в средних погашается неполностью, в силу недостаточно большого количества наблюдений, поэтому эмпирической линией связи для выбора и обоснования типа теоретической кривой можно воспользоваться при условии, что число наблюдений будет достаточно велико. [2, с.257]

Одним из элементов конкретных исследований является сопоставление различных уравнений зависимости, основанное на использовании критериев качества аппроксимации эмпирических данных конкурирующими вариантами моделей Наиболее часто для характеристики связей экономических показателей используют следующие типы функций:

Логистическая: [2, c.258]

Модель с одной объясняющей и одной объясняемой переменными – модель парной регрессии. Если объясняющих (факторных) переменных используется две или более, то говорят об использовании модели множественной регрессии. При этом, в качестве вариантов могут быть выбраны линейная, экспоненциальная, гиперболическая, показательная и другие виды функций, связывающие эти переменные.

Для нахождения параметров а и b уравнения регрессии используют метод наименьших квадратов. При применении метода наименьших квадратов для нахождения такой функции, которая наилучшим образом соответствует эмпирическим данным, считается, что сумка квадратов отклонений эмпирических точек от теоретической линии регрессии должна быть величиной минимальной.

Критерий метода наименьших квадратов можно записать таким образом:

Следовательно, применение метода наименьших квадратов для определения параметров a и b прямой, наиболее соответствующей эмпирическим данным, сводится к задаче на экстремум. [2, c.258]

Относительно оценок можно сделать следующие выводы:

Оценки метода наименьших квадратов являются функциями выборки, что позволяет их легко рассчитывать.

Оценки метода наименьших квадратов являются точечными оценками теоретических коэффициентов регрессии.

Эмпирическая прямая регрессии обязательно проходит через точку x, y.

Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений .

Графическое изображение эмпирической и теоретической линии связи представлено на рисунке 1.

неизвестных параметров хорошо развита именно в случае линейного регрессионного анализа. Если же линейности нет и нельзя перейти к линейной задаче, то, как правило, хороших свойств от оценок ожидать не приходится. Продемонстрируем подходы в случае зависимостей различного вида. Если зависимость имеет вид многочлена (полинома). Если расчёт корреляции характеризует силу связи между двумя переменными, то регрессионный анализ служит для определения вида этой связи и дает возможность для прогнозирования значения одной (зависимой) переменной отталкиваясь от значения другой (независимой) переменной. Для проведения линейного регрессионного анализа зависимая переменная должна иметь интервальную (или порядковую) шкалу. В то же время, бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа. Если зависимая переменная является категориальной, но имеет более двух категорий, то здесь подходящим методом будет мультиномиальная логистическая регрессия можно анализировать и нелинейные связи между переменными, которые относятся к интервальной шкале. Для этого предназначен метод нелинейной регрессии. [10]

ГЛАВА 2 . МОДЕЛИ РЕГРЕССИИ

2.1. Парная линейная регрессия

Можно выделить три основных класса моделей, которые применяются для анализа и прогнозирования экономических процессов:

модели временных рядов,

регрессионные модели с одним уравнением,

системы одновременных уравнений.

Линейная регрессия представляет собой линейную функцию между условным математическим ожиданием зависимой переменной Y и одной объясняющей переменной X:

где - значения независимой переменной в i-ом наблюбдении, i=1,2,…,n. Принципиальной является линейность уравнения по параметрам , . Так как каждое индивидуальное значение отклоняется от соответствующего условного математического ожидания, тогда вданную формулу необходимо ввести случайное слагаемое , тогда получим:

Данное соотношение называется теоретической линейной регрессионной моделью, а и - теоретическими параметрами (теоретическими коэффициентами) регрессии, - случайным отклонением. Следовательно, индивидуальные значения представляются в виде суммы двух компонент – систематической и случайной [12]

Для определения значений теоретических коэффициентов регрессии необходимо знать и использовать все значения переменных X и Y генеральной совокупности, что невозможно. задачи регрессионного линейного анализа состоят в том, чтобы по имеющимся статистическим данным ( ), i=1,…,n для переменных X и Y:

получить наилучшие оценки неизвестных параметров и ;

проверить статистические гипотезы о параметрах модели;

проверить, достаточно ли хорошо модель согласуется со статистическими данными.

где r - коэффициент линейной корреляции Пирсона для переменных x и y; s x и s y - стандартные отклонения для переменных x и y; x,y - средние арифметические для переменных x и y.

Существуют два подхода к интерпретации коэффициента регрессии b. Согласно первому из них, b представляет собой величину, на которую изменяется предсказанное по модели значение ŷ i = a + bx i при увеличении значения независимой переменной x на одну единицу измерения, согласно второй - величину, на которую в среднем изменяется значение переменной y i при увеличении независимой переменной x на единицу. На диаграмме рассеяния коэффициент b представляет тангенс угла наклона линии регрессии y = a + bx к оси абсцисс. Знак коэффициента регрессии совпадает со знаком коэффициента линейной корреляции: значение b>0 свидетельствует о прямой линейной связи, значение b k -мерном пространстве, отклонение результатов наблюдений от которой были бы минимальными. Используя для этого метод наименьших квадратов, получается система нормальных уравнений, которую можно представить и в матричной форме.

Множественная линейная регрессия - причинная модель статистической связи линейной между переменной зависимой y и переменными независимыми x 1 ,x 2 . x k , представленная уравнением y = b 1 x 1 + b 2 x 2 + . + b k x k + a = ∑ b i x i + a . Коэффициенты b 1 ,b 2 . b k называются нестандартизированными коэффициентами, а - свободным членом уравнения регрессии. Уравнение регрессии существует также в стандартизированном виде, когда вместо исходных переменных используются их z-оценки: z y = ∑ β i z i . Здесь z y - z-оценка переменной у; z 1 ,z 2 . z k - z-оценки переменных x 1 ,x 2 . x k ; β 1 ,β 2 . β k - стандартизированные коэффициенты регрессии (свободный член отсутствует).

Для того чтобы найти стандартизированные коэффициенты, необходимо решить систему линейных уравнений:

β 1 + r 12 β 2 + r 13 β 3 + . + r 1 k β k = r 1 y ,

r 21 β 1 + β 2 + r 23 β 3 + . + r 2 k β k = r 2 y ,

r 31 β 1 + r 32 β 2 + β 3 + . + r 3 k β k = r 3 y ,

r k 1 β 1 + r k 2 β 2 + r k 3 β 3 + . + β k = r ky ,

в которой r ij - коэффициенты линейной корреляции Пирсона для переменных x i и x j ; r iy - коэффициент корреляции Пирсона для переменных x i и y. [8]

Нестандартизированные коэффициенты регрессии вычисляются по формуле b i = β i ∙ s y / s i , где s y - стандартное отклонение переменной y; s i - стандартное отклонение переменной х i . Свободный член уравнения регрессии находится по формуле a = y - ∑ b i x i , где y - среднее арифметическое переменной y, x i - средние арифметические для переменных x i .

В настоящее время используются два подхода к интерпретации нестандартизированных коэффициентов линейной регрессии b i . Согласно первому из них, b i представляет собой величину, на которую изменится предсказанное по модели значение ŷ = ∑ b i x i при увеличении значения независимой переменной x i на единицу измерения; согласно второму - величину, на которую в среднем изменяется значение переменной y при увеличении независимой переменной x i на единицу. Значения коэффициентов b i существенно зависят от масштаба шкал, по которым измеряются переменные y и x i , поэтому по ним нельзя судить о степени влияния независимых переменных на зависимую. Свободный член уравнения регрессии a равен предсказанному значению зависимой переменной ŷ в случае, когда все независимые переменные x i = 0. [8]

Стандартизированные коэффициенты β i являются показателями степени влияния независимых переменных x i на зависимую переменную y. Они интерпретируются как "вклад" соответствующей независимой переменной в дисперсию (изменчивость) зависимой переменной.

Качество (объясняющая способность) уравнения множественной линейной регрессии измеряется коэффициентом множественной детерминации, который равен квадрату коэффициента корреляции множественной R².

Предполагается, что все переменные в уравнении множественной линейной регрессии являются количественными. При необходимости включить в модель номинальные переменные используется техника dummy-кодирования.

ЗАКЛЮЧЕНИЕ

При наличии нескольких показателей задача регрессионного анализа решается независимо для каждого из них. Анализируя сущность уравнения регрессии, следует отметить следующие положения. Изменение значений других. Полученные коэффициенты не следует рассматривать как вклад соответствующего параметра в значение показателя. Уравнение регрессии является всего лишь хорошим аналитическим описанием имеющихся экономических данных, а не законом, описывающим взаимосвязи параметров и показателя. Это уравнение применяют для расчета значений показателя в заданном диапазоне изменения параметров. Оно ограниченно пригодно для расчета вне этого диапазона, т.е. его можно применять для решения задач интерполяции и в ограниченной степени для экстраполяции.

Главной причиной неточности прогноза является не столько неопределенность экстраполяции линии регрессии, сколько значительная вариация показателя за счет неучтенных в модели факторов. Ограничением возможности прогнозирования служит условие стабильности неучтенных в модели параметров и характера влияния учтенных факторов модели. Если резко меняется внешняя среда, то составленное уравнение регрессии потеряет свой смысл. Нельзя подставлять в уравнение регрессии такие значения факторов, которые значительно отличаются от представленных/ Рекомендуется не выходить за пределы одной трети размаха вариации параметра как за максимальное, так и за минимальное значения фактора.

СПИСОК ЛИТЕРАТУРЫ

Елисеева И.И., Юзбашев М.М. Общая теория статистики. – Москва: Финансы и статистика, 2004. – 656с.

Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: Инфра-М, 2004. – 416с.

Общая теория статистики/ под ред. О.Э. Башиной, А.А. Спирина.– М.: Финансы и статистика, 2005. – 440с.

Сизова Т.М. Статистика. - СПб.: СПбГУ ИТМО, 2005. - 190 с.

Теория статистики/ под ред. Г.Л.Громыко. – М.: Инфра-М, 2005. – 476с.

Теория статистики/ под ред. Р.А.Шмойловой. – М.: Финансы и статистика, 2009. –656с.

Уравнение регрессии для Rсж28нт образцов раствора 1 3 на смешанном цементно туфовом вяжущим с использованием

. 0 700 300 7,0 Таблица 3 – Определение коэффициентов уравнения регрессии № п/п Матрица планирования Квадратичные переменные Взаимодействие . числе и незначимые коэффициенты уравнения регрессии. Таким образом, уравнение регрессии необходимо сохранить в исходном .

Уравнения регрессии

. для уравнения линейной регрессии, следовательно, все остальные уравнения регрессии ненадежны. Итак, уравнение линейной регрессии является лучшим уравнением регрессии .

Уравнения регрессии. Коэффициент эластичности, корреляции, детерминации и F-критерий Фишера

. ,0 Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров. уравнение регрессии По методу . наименьших квадратов. Расчётная таблица уравнение регрессии При увеличении .

Коэффициент детерминации. Значимость уравнения регрессии

. уравнения регрессии. Рассчитаем значение F-критерия Фишера по формуле: Уравнение регрессии . уравнения нелинейной регрессии: гиперболической, степенной, показательной. Привести графики построенных уравнений регрессии. Построение степенной модели. Уравнение .

Линейное уравнение регрессии

. о значимости уравнения регрессии проверьте с помощью F-критерия Фишера; оцените качество уравнения регрессии с помощью . гипотезу о значимости уравнения регрессии проверим с помощью F-критерия; оценим качество уравнения регрессии с помощью коэффициента .

1.1. Уравнение регрессии: сущность и типы функций

Регрессия (лат. regressio- обратное движение, переход от более сложных форм развития к менее сложным) - одно из основных понятий в теории вероятности и математической статистике, выражающее зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин. Это понятие введено Фрэнсисом Гальтоном в 1886. [9]

y=f(x) - уравнение регрессии - это формула статистической связи между переменными.

7. Логистическая: [2, c.258]

Критерий метода наименьших квадратов можно записать таким образом:

Относительно оценок можно сделать следующие выводы:

1. Оценки метода наименьших квадратов являются функциями выборки, что позволяет их легко рассчитывать.

2. Оценки метода наименьших квадратов являются точечными оценками теоретических коэффициентов регрессии.

3. Эмпирическая прямая регрессии обязательно проходит через точку x, y.

4. Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений .

Графическое изображение эмпирической и теоретической линии связи представлено на рисунке 1.

1. модели временных рядов,

2. регрессионные модели с одним уравнением,

3. системы одновременных уравнений.

Для определения значений теоретических коэффициентов регрессии необходимо знать и использовать все значения переменных Xи Y генеральной совокупности, что невозможно. задачи регрессионного линейного анализа состоят в том, чтобы по имеющимся статистическим данным (), i=1,…,nдля переменных Xи Y:

1. получить наилучшие оценки неизвестных параметров и ;

2. проверить статистические гипотезы о параметрах модели;

3. проверить, достаточно ли хорошо модель согласуется со статистическими данными.

где r - коэффициент линейной корреляции Пирсона для переменных x и y; s_x и s_y - стандартные отклонения для переменных x и y; x,y - средние арифметические для переменных x и y.

Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.

! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.

Содержание

Введение

Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.

Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.

В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций

Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию (которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).

Точки генерируются случайно по распределению Гаусса с заданным средним и вариациями. Синяя линия — регрессионная прямая.

Метод наименьших квадратов

Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости и мы ищем такую аффинную функцию

чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной .

Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого поэтому измерять нужно вдоль оси .

Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц . Простейший вариант — сумма модулей отклонений приводит к Least Absolute Distance (LAD) регрессии.

Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)

Метод наименьших квадратов (по англ. OLS) — линейная регрессия c в качестве функции потерь.

Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу .

Регрессионная прямая (синяя) и пробная прямая (зеленая). Справа показана функция потерь и точки соответствующие параметра пробной и регрессионной прямых.

Математический анализ

Простейший способ найти — вычислить частные производные по и , приравнять их нулю и решить систему линейных уравнений

Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям

которые легко решить

Мы получили громоздкие и неструктурированные выражения. Сейчас мы их облагородим и вдохнем в них смысл.

Статистика

Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего , вариации (стандартного отклонения), ковариации и корреляции

где это нескорректированное (смещенное) стандартное выборочное отклонение, а — ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)

Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так

прямая проходит через центр масс ;
если по оси за единицу длины выбрать , а по оси — , то угол наклона прямой будет от до . Это связано с тем, что .

Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации . Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные. , равный , означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения

— вариация исходных данных (вариация точек ).

— вариация остатков, то есть вариация отклонений от регрессионной модели — от нужно отнять предсказание модели и найти вариацию.

— вариация регрессии, то есть вариация предсказаний регрессионной модели в точках (обратите внимание, что среднее предсказаний модели совпадает с ).

Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)

Как видим, стандартные отклонения образуют прямоугольный треугольник.

Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует , равный единице минус доля вариации ошибок в суммарной вариации

или доле объясненной вариации (доля вариации регрессии в полной вариации)

равен косинусу угла в прямоугольном треугольнике . Кстати, иногда вводят долю необъясненной вариации и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.

Теория вероятностей

Ранее мы пришли к функции потерь из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например и ). Для этого нужно вычислить вероятность получить датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.

Вернемся к задаче простой регрессии. Допустим, что значения нам известны точно, а в измерении присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда

где — нормально распределенная случайная величина

Таким образом, максимум правдоподобия достигается при минимуме

что дает основание принять ее в качестве функции потерь. Кстати, если

мы получим функцию потерь LAD регрессии

которую мы упоминали ранее.

Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.

Мультилинейная регрессия

До сих пор мы рассматривали задачу регрессии для одного скалярного признака , однако обычно регрессор — это -мерный вектор . Другими словами, для каждого измерения мы регистрируем фич, объединяя их в вектор. В этом случае логично принять модель с независимыми базисными функциями векторного аргумента — степеней свободы соответствуют фичам и еще одна — регрессанту . Простейший выбор — линейные базисные функции . При получим уже знакомый нам базис .

Итак, мы хотим найти такой вектор (набор коэффициентов) , что

Знак "" означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок

Последнее уравнение можно переписать более удобным образом. Для этого расположим в строках матрицы (матрицы информации)

Тогда столбцы матрицы отвечают измерениям -ой фичи. Здесь важно не запутаться: — количество измерений, — количество признаков (фич), которые мы регистрируем. Систему можно записать как

Квадрат нормы разности векторов в правой и левой частях уравнения образует функцию потерь

которую мы намерены минимизировать

Продифференцируем финальное выражение по (если забыли как это делается — загляните в Matrix cookbook)

приравняем производную к и получим т.н. нормальные уравнения

Если столбцы матрицы информации линейно независимы (нет идеально скоррелированных фич), то матрица имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать

псевдообратная к . Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.

Напомню, что обратить и найти можно только если столбцы линейно независимы. Впрочем, если столбцы близки к линейной зависимости, вычисление уже становится численно нестабильным. Степень линейной зависимости признаков в или, как говорят, мультиколлинеарности матрицы , можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе к вырожденной и неустойчивее вычисление псевдообратной.

Линейная алгебра

К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению

Если количество переменных равно количеству неизвестных и уравнения линейно независимы, то система имеет единственное решение. Однако, если число измерений превосходит число признаков, то есть уравнений больше чем неизвестных — система становится несовместной, переопределенной. В этом случае лучшее, что мы можем сделать — выбрать вектор , образ которого ближе остальных к . Напомню, что множество образов или колоночное пространство — это линейная комбинация вектор-столбцов матрицы

— -мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов . Итак, если принадлежит , то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.

Если в дополнение к векторам мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай , тогда

где . В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.

Если мы ищем решение , то естественно потребовать, чтобы была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора

но поскольку, выбрав подходящий , я могу получить любой вектор колоночного пространства, то задача сводится к

а останется в качестве неустранимой ошибки. Любой другой выбор сделает ошибку только больше.

что очень удобно, так как у нас нет, а вот — есть. Вспомним из предыдущего параграфа, что имеет обратную при условии линейной независимости признаков и запишем решение

где уже знакомая нам псевдообратная матрица. Если нам интересна проекция , то можно записать

где — оператор проекции на колоночное пространство.

Выясним геометрический смысл коэффициента детерминации.

Заметьте, что фиолетовый вектор пропорционален первому столбцу матрицы информации , который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике

Так как этот треугольник прямоугольный, то по теореме Пифагора

Это геометрическая интерпретация уже известного нам факта, что

Красиво, не правда ли?

Произвольный базис

но до сих пор мы использовали простейшие , которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей . Как можно было заметить, на самом деле ни вид , ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки ложатся на параболу, а не на прямую, то стоит выбрать базис . Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.

Регрессия в полиномиальном базисе. Выделенная часть кода демонстрирует использование стандартных функций scikit-learn для выполнения регрессии полиномами разной степени, снизу — визуализация результата работы.

Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации

записываем функцию потерь

и находим её минимум, например с помощью псевдообратной матрицы

Заключительные замечания

Проблема выбора размерности

Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент

где — размер выборки, — количество независимых переменных. Следя за , мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.

Вторая группа подходов — регуляризации, самые известные из которых Ridge(/гребневая/Тихоновская регуляризация), Lasso( регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов неограниченно расти и тем самым воспрепятствуют переобучению

Численные методы

Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.

Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.

Реклама и заключение

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t‑критерия Стьюдента

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью - критерия Фишера , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя при уровне значимости , если прогнозное значения фактора Х составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения точки прогноза.

8. Составить уравнения нелинейной регрессии:

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Раздел: Экономико-математическое моделирование
Количество знаков с пробелами: 18722
Количество таблиц: 16
Количество изображений: 4

Похожие работы

объема экспериментальных исследований. Применение современной вычислительной техники позволяет в ряде случаев упростить процедуру определения релаксационных констант. Особенно этот метод эффективен, с нашей точки зрения, при изучении релаксационных процессов в модифицированных полимерных материалах, когда известны релаксационные константы полимера-связующего. Суть подхода в определении U, Tm и B .

. по данным производственных измерений. Таким образом, найденное уравнение регрессии описывает совместное влияние x 1 и x2 на функцию у. Коэффициенты a, b 1 и b 2 при этом имеют математический смысл. Коэффициент а равен функции у при нулевых значениях аргументов x1 и x 2. В геометрической интерпретации коэффициент а соответствует ординате точки пересечения плоскости регрессии Р с осью .

На предыдущем уроке мы уже узнали, что такое линейная регрессия и научились находить её уравнение для несгруппированных данных (это когда даны две строчки или два столбца чисел). И сейчас тема получает продолжение – в данной статье я расскажу вам о том, как вычислить линейный коэффициент корреляции и как найти уравнение линейной регрессии в случае комбинационной группировки. Это когда в условии дана комбинационная таблица:

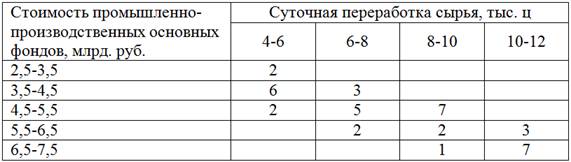
Имеются выборочные данные по 40 предприятиям региона:

1) Определить признак-фактор и признак-результат и высказать предположение о наличии и направлении корреляционной зависимости от . Построить корреляционное поле и выдвинуть гипотезу о возможной форме зависимости.

2) Вычислить линейный коэффициент корреляции и детерминации, сделать выводы.

3) Найти уравнение линейной регрессии на и изобразить соответствующую прямую на чертеже. Спрогнозировать среднюю суточную переработку сырья, когда стоимость основных фондов предприятий достигнет 9 млрд. руб.

Все термины и понятия вам уже знакомы! А если нет, то будут ссылки по ходу решения и, конечно же, видео – как это всё быстро подсчитать и нарисовать в Экселе + Калькулятор (сразу для особо страждущих).

1) Прежде всего в подобных задачах нам нужно обосновать причинно-следственную связь между признаками (если это не сделано в условии). Очевидно, что чем больше стоимость основных фондов, тем крупнее предприятие и тем больше сырья оно способно переработать. Однако это не является непреложным правилом, ибо любое, самое крупное предприятие может неэффективно работать или даже простаивать. Тем не менее, общая тенденция состоит в том, что при увеличении стоимости фондов предприятий их средняя суточная переработка растёт. Такая нежёсткая зависимость называется… Правильно! Я приду к вам в вещих снах – будете вздрагивать и просыпаться от этой фразы :)

Таким образом, мы предполагаем наличие прямой корреляционной зависимости суточной переработки сырья (признак-результат) от стоимости основных фондов (фактор ).

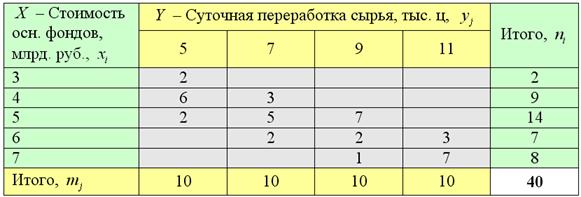
Теперь определим форму зависимости (линейная, квадратичная, экспоненциальная или какая-то другая). Простейший способ – графический, построили корреляционное поле и посмотрели. Для этого нужно немного модифицировать исходную таблицу, а именно перейти от интервальных вариационных рядов (левый столбец и 2-я сверху строка) к дискретным, выбрав в качестве вариант и середины соответствующих интервалов:

Заодно подсчитаем суммы частот по серым строкам (правый столбец) и суммы частот по серым столбцам (нижняя строка), не забыв убедиться в том, что итоговые суммы равны объёму выборки :

Довольно часто значения и уже подсчитаны и приведены в условии, но так бывает не во всех задачах, и поэтому я насыщаю решение всеми возможными действиями.

2) Коэффициент корреляции вычислим по знакомой формуле .

Лично я привык в первую очередь находить средние и стандартные отклонения . Эти расчёты мы проводили неоднократно.

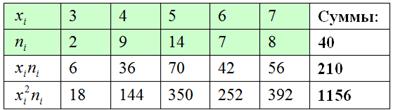
Сначала разберёмся с признаком-фактором . Для этого из комбинационной таблицы (см. выше) выпишем значения и заполним расчётную таблицу:

Вычислим среднее значение млрд. руб. и среднее квадратическое отклонение, как корень из дисперсии, вычисленной по формуле:

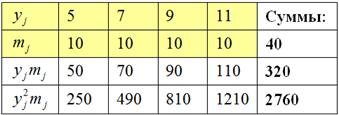
Аналогично, берём игрековые значения из комбинационной таблицы и заполняем расчетную таблицу для признака-результата :

после чего рассчитываем нужные показатели:
тыс. ц;

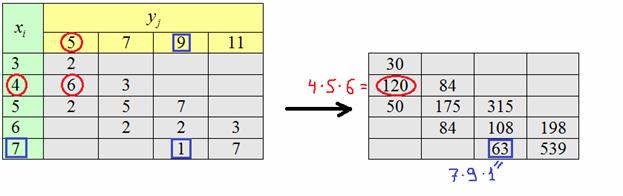
Теперь найдём среднее значение произведения признаков. Для этого вычислим все возможные произведения и на соответствующие ненулевые частоты , наглядно распишу парочку штук:

Вычислим сумму этих произведений:

и искомую среднюю:

Таким образом, линейный коэффициент корреляции:

В результате получено положительное число и, согласно шкале Чеддока, существует сильная прямая линейная корреляционная зависимость суточной переработки сырья от стоимости основных фондов.

Вычислим коэффициент детерминации:
, таким образом, в рамках построенной модели 69,12% вариации суточной переработки сырья обусловлено стоимостью основных фондов. Остальные вариации обусловлено другими факторами.

В статье об индексе корреляции и детерминации я более подробно разберу построенную модель, и тогда последний вывод станет понятнее (для тех, кому он не очень понятен).

3) Найдём уравнение линейной регрессии на (именно так на). Здесь можно использовать формулы предыдущего урока , но есть более академичный вариант. Искомое уравнение имеет вид:
, в данной задаче (вычисления приближённые):

Полученное уравнение показывает, что при увеличении стоимости основных фондов на 1 млрд. руб. суточная переработка сырья увеличивается в среднем на 1,61 тысяч центнеров.

Найдём пару удобных точек для построения графика:

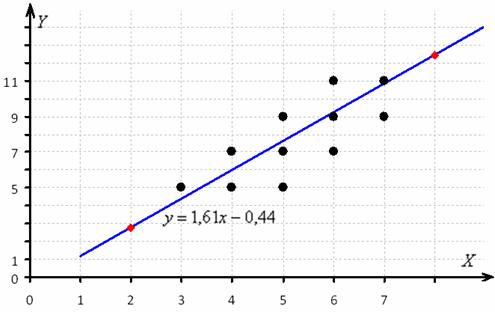
отметим их на чертеже (красный цвет) и аккуратно проведём линию регрессии, её, как правило, изображают на том же чертеже:

Спрогнозируем среднюю суточную переработку сырья при стоимости основных фондов в 9 млрд. руб.:
тыс. ц.

Как найти коэффициент корреляции и уравнение регрессии по таблице? (Ютуб)

Для желающих сразу решить эту задачу есть калькулятор.

Чисто формально эта регрессия существует всегда, так, в рассмотренной задаче признак явно не зависит от , но вот линейная корреляционная зависимость есть! (причём, такой же тесноты). Помним, что причинно-следственная зависимость и корреляционная – это не одно и то же! Кроме того, в некоторых задачах признаки взаимно влияют друг на друга, уже известный вам пример:

– количество произведённых куриц на птицефабрике;
– количество произведённых яиц.

Здесь в уравнении регрессии на – самый что ни на есть здравый смысл.

График регрессии тоже можно изобразить на чертеже, и примечателен тот факт, что он будет пересекать график в точности в точке .

Следует добавить, что второе уравнение регрессии можно построить и для случая несгруппированных данных (см. задачи предыдущего урока о корреляции). Формула та же.

И я предлагаю вам потренироваться самостоятельно:

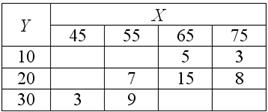
Известны следующие данные:

Найти линейный коэффициент корреляции и уравнения регрессии на и на . Построить корреляционное поле, линии регрессии и определить их точку пересечения. Вычислить и . По каждому пункту сделать выводы.

Обратите внимание, что в условии ничего не сказано о признаках , но нам ничего и не нужно о них знать, ведь задачу можно решить вне зависимости от того, где здесь признак-фактор, а где результат, и есть ли вообще причинно-следственная связь между признаками. Хотя, скорее всего, она здесь есть, ибо комбинационная группировка выполнена же из каких-то соображений.

Все числа уже в Экселе и вам остаётся выполнить вычисления; ничего страшного, если получится не очень красиво, важно наработать сам навык. Краткое решение для сверки чуть ниже.

Для читателей с углублённым изучением статистики и просто энтузиастов запланирована статья об Индексе корреляции и проверке значимости коэффициентов (там на самом деле много ещё чего). Далее поговорим о моделях нелинейной регрессии, ранговой корреляции Спирмена, коэффициенте корреляции Фехнера. И вишенка на торте, точнее, тыква на голове:))

Множественная корреляция и модель двухфакторной регрессии.

Впрочем, это пока ориентировочные планы.

До скорых встреч!

Решения и ответы:

Пример 70. Решение: вычислим частоты по каждому признаку:

Линейный коэффициент корреляции найдём по формуле .
Заполним расчётную таблицу для признака :

Вычислим среднее значение и среднее квадратическое отклонение:

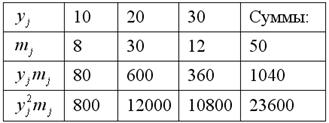
Заполним расчётную таблицу для признака :

Вычислим и
.

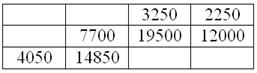
Вычислим произведения :

их сумму и среднюю .

Вычислим линейный коэффициент корреляции:
, таким образом, существует заметная обратная линейная корреляционная зависимость между признаками (в обе стороны).

Найдём точки для построения графиков:

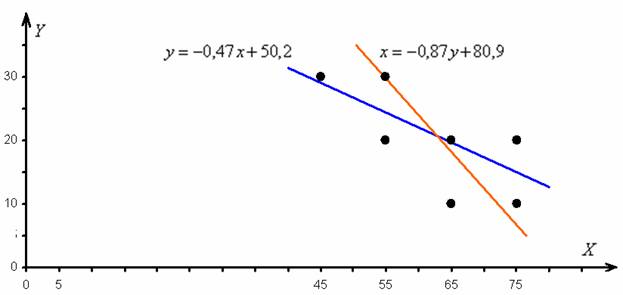
построим корреляционное поле и изобразим линии регрессии:

Линии регрессии пересекаются в точке

Примечание: вычисления местами не очень точные из-за округлений.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Читайте также:

Составление и решение уравнений линейной регрессии доклад

ГЛАВА 1. УРАВНЕНИЕ РЕГРЕССИИ: ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

1.1. Уравнение регрессии: сущность и типы функций

ГЛАВА 2 . МОДЕЛИ РЕГРЕССИИ

2.1. Парная линейная регрессия

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

Похожие страницы:

Уравнение регрессии для Rсж28нт образцов раствора 1 3 на смешанном цементно туфовом вяжущим с использованием

Уравнения регрессии

Уравнения регрессии. Коэффициент эластичности, корреляции, детерминации и F-критерий Фишера

Коэффициент детерминации. Значимость уравнения регрессии

Линейное уравнение регрессии

1.1. Уравнение регрессии: сущность и типы функций

Содержание

Введение

Метод наименьших квадратов

Математический анализ

Статистика

Теория вероятностей

Мультилинейная регрессия

Линейная алгебра

Произвольный базис

Заключительные замечания

Проблема выбора размерности

Численные методы

Реклама и заключение

Похожие работы